矩阵链乘法
什么是矩阵乘法?
这是线性代数最重要的一个部分,这里我直接写矩阵乘法的代码:
1 | int ans[maxn][maxn]; |
从代码我们可以看出,一共要进行三重循环,对于矩阵$a[a_m][a_n]$和 $b[b_m][b_n]$ 来说,他们能够相乘,那么必然 $a_n=b_m$
那么这个算法一共要进行的乘法计算次数为:$a_ma_nb_n$
比如说,对于矩阵 $A_1[10][100],A_2[100][5]$ 来说,他们要相乘,乘法运算的次数为: $10\cdot100\cdot5=5000$次
什么是 矩阵链 乘法?
给定 n 个矩阵的链 $
我们以矩阵链$
但是,如果按$(A_1(A_2A_3))$ 的顺序.计算$A_2A_3$(计算后矩阵规模为 $100\times 50$), 需100 ·5·50=25000次标量乘法, 再与$A_1$相乘又需10•100• 50=50 000次标鬟乘法. 共需75000次标量乘法. 因此.按第一种顺序计算矩阵链乘积要比第二种顺序快10倍.
用动态规划方法求解
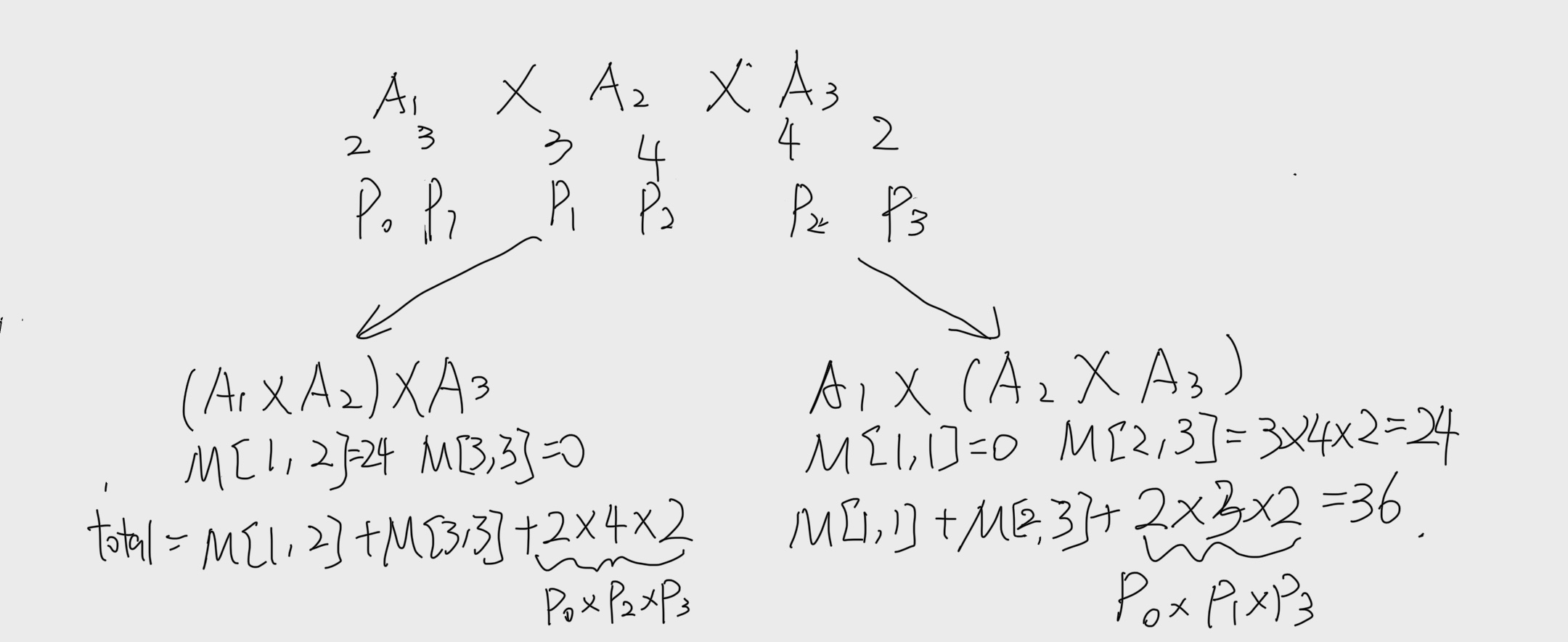
我们可以这么来理解:令 $m[i,j]$ 表示计算矩阵 $A_i\cdots A_j$ 所需标量乘法次数的最小值,那么原问题的最优解 就变成了 $m[1,n]$
我们可以递归定义$m[i,j]$如下. 对于 $i,j$ 时的平凡问题.矩阵链只包含唯一的矩阵,那么这时候就不用做任何的标量乘法运算。所以,对所有的 $i = 1,2,\cdots,n,m[i,i]=0 $ .我们假设 $AiA{i+1}\cdots Aj$ 的最优括号化方案的分割点再矩阵 $A_k$ 和 $A{k+1}$ 之间,其中 $i\leq k<j$,那么,$m[i,j]$ 就等于计算 $A{i\cdots k}$ 和 $A{k+1\cdots j}$ 相乘的代价为 $p_{i-1}p_kp_i$次标量乘法运算。因此,我们得到:
$m[i,j] = m[i,k]+m[k+1,j]+p_{i-1}p_kp_j$
此递归公式假定最优分割点k是已经知道的,但是事实上我们并不知道。不过 k只有 j-i种可能。由于最优分割点必在这其中,我们只要检查所有可能的情况。找到最优解即可。因此我们可以写出下面这个递归公式
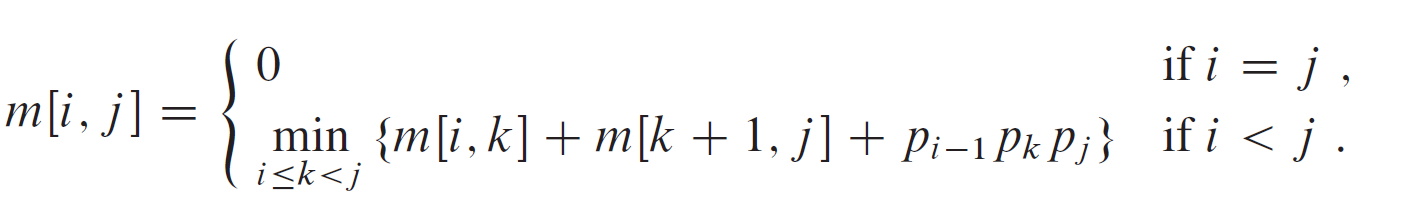
比如说对于一个长为4 的矩阵链,我们可以这样将他的完整的递归链条写出来。
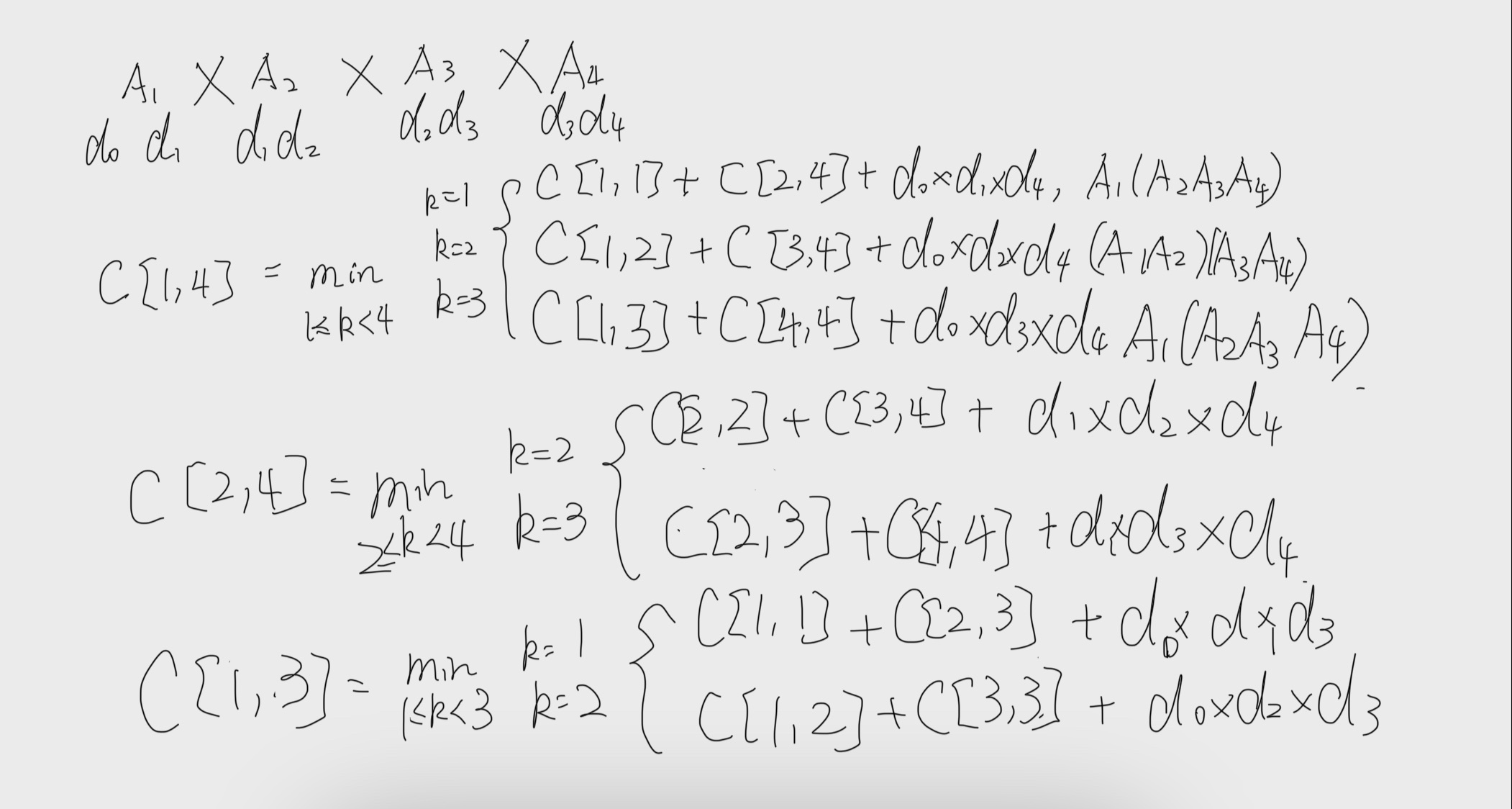
但这样写十分庞杂,我们可以将它整合到一个 i * j 的棋盘格当中。
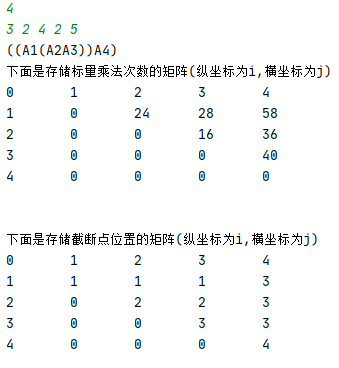
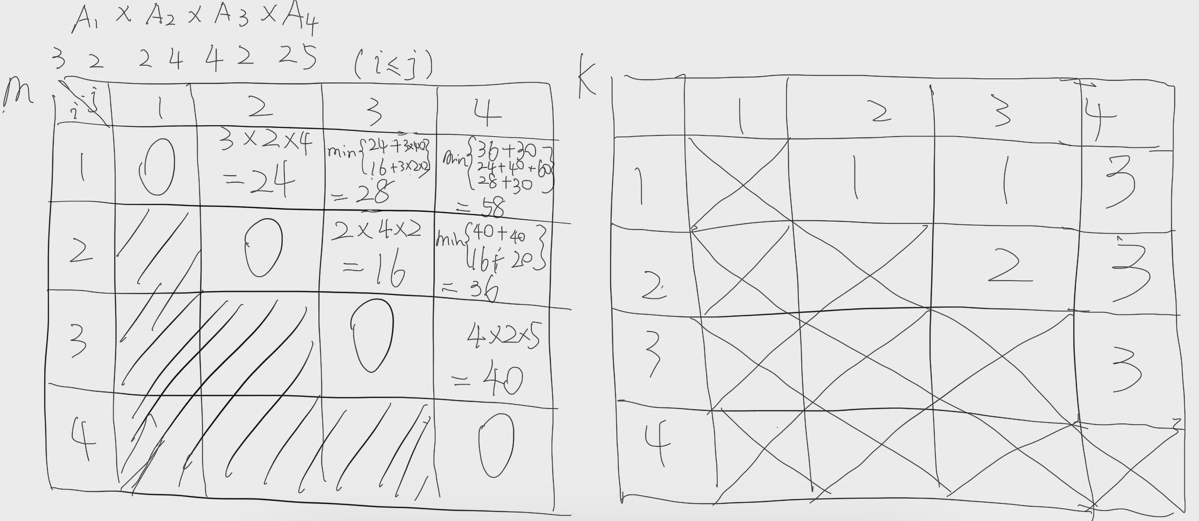
比如说题目是这样的:
代码
1 |
|
那么对于刚才的题目,我们可以输出 m矩阵和k矩阵,并且给出最优的括号解