卷积神经网路理论
Convolutional Neural Networks

对于这张图片,我们会产生一种错觉:图片中的人是向右看的还是向前看的。我们发现如果我们观察这个人的右轮廓,就会觉得这个人是向右看的。如果我们直视这个人的眼睛和耳朵,那么就会觉得这个人是向前看的。因此我们可以推断出我们看见什么取决于大脑看见的特征.

又比如说这一张图,我们如果看红色的轮廓,那我们会认为这是一个年轻的小孩正在侧脸注视前方。但是如果我们看蓝笔画出的轮廓,就会观察到一个老婆婆低下头打着盹。

最后一张图片,让我们的大脑变得无所适从——我们会在两张脸的特征上跳来跳去,导致一开始这张图片会有些眼花缭乱的感觉。
这三个例子都在告诉我们我们的大脑是怎么运作的:大脑分析处理现实生活中看到的东西的特征然后经过处理得到我们认知的图像。这就导致了我们会出现很多错觉。
在卷积神经网络当中,机器处理分析图像的方式和我们的大脑非常类似。
现在我们来看一些例子:下面三张图片是神经网络预测的图片
前两幅图计算机都非常准确得预测了照片中的物体,但是对于第三张图片的预测却出现了偏差。这是因为第三张图片本身拍摄的就不是非常清晰,特征也不是很明显,下面几个选项的描述也有点模糊。因此机器预测这个图片中的物品是剪刀而不是放大镜

这是CNN(卷积神经网络) 的简易模型:
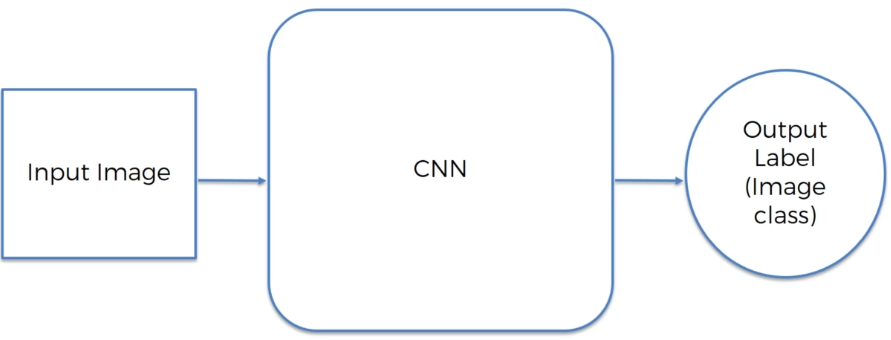
比如说:
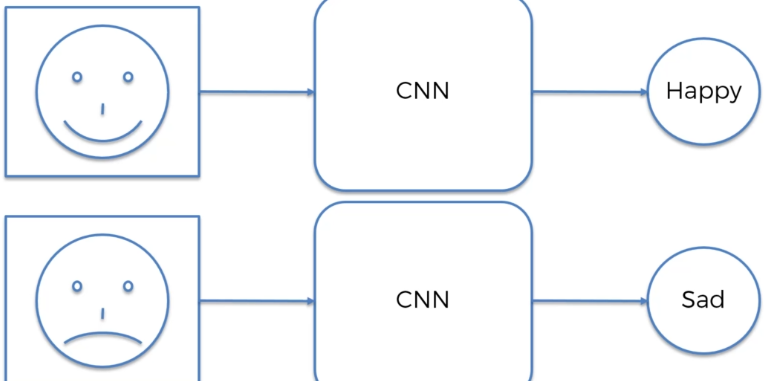
卷积神经网络并不会给出一个100%的概率,这就好像有时候我们会对别人的表情神态判断错误一样
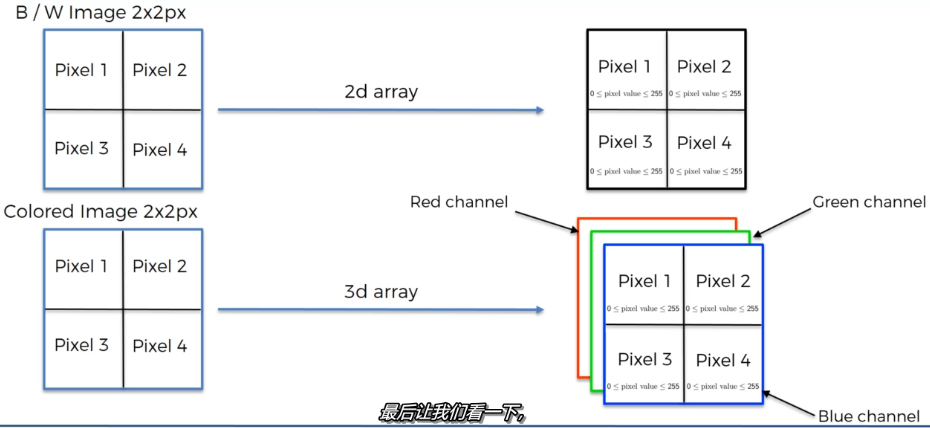
对于一幅图片,我们知道它是由像素组成的。在电脑里,一张图片就表现为一个矩阵。比如说一张2x2像素的灰白图,在电脑里就是一个2x2的矩阵,每个元素的取值范围是 (0,255)
如果是一张彩色的照片,那么我们就需要3个2x2的矩阵来对其进行存储,因为色彩是由3个维度的数据RGB组成的。
计算机怎么读取图片
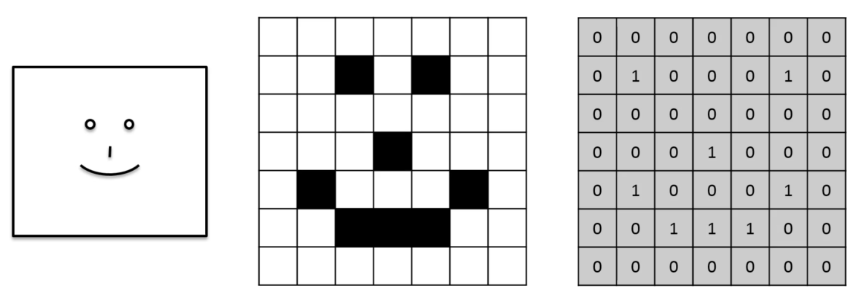
比如说一个笑脸的照片,我们可以用01矩阵来存储:0代表白,1代表黑
卷积网络的步骤
STEP1: Convolution 卷积
STEP2: Max Pooling 最大池化
STEP3: Flattening 平坦化
STEP4: Full Connection 全连接
Convolution
这是卷积的公式,但是这里我们并不会过多的解释数学层面的,因此其内部的原理可以参考这篇文章:
http://cs.nju.edu.cn/wujx/paper/CNN.pdf
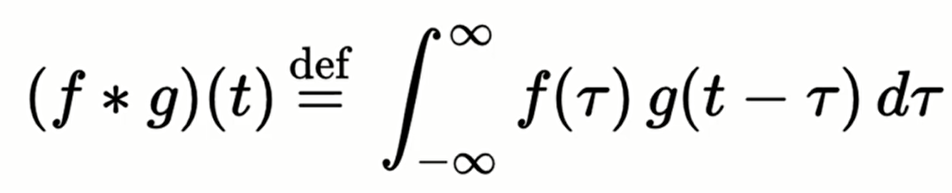
那么,卷积的直观含义是什么呢?
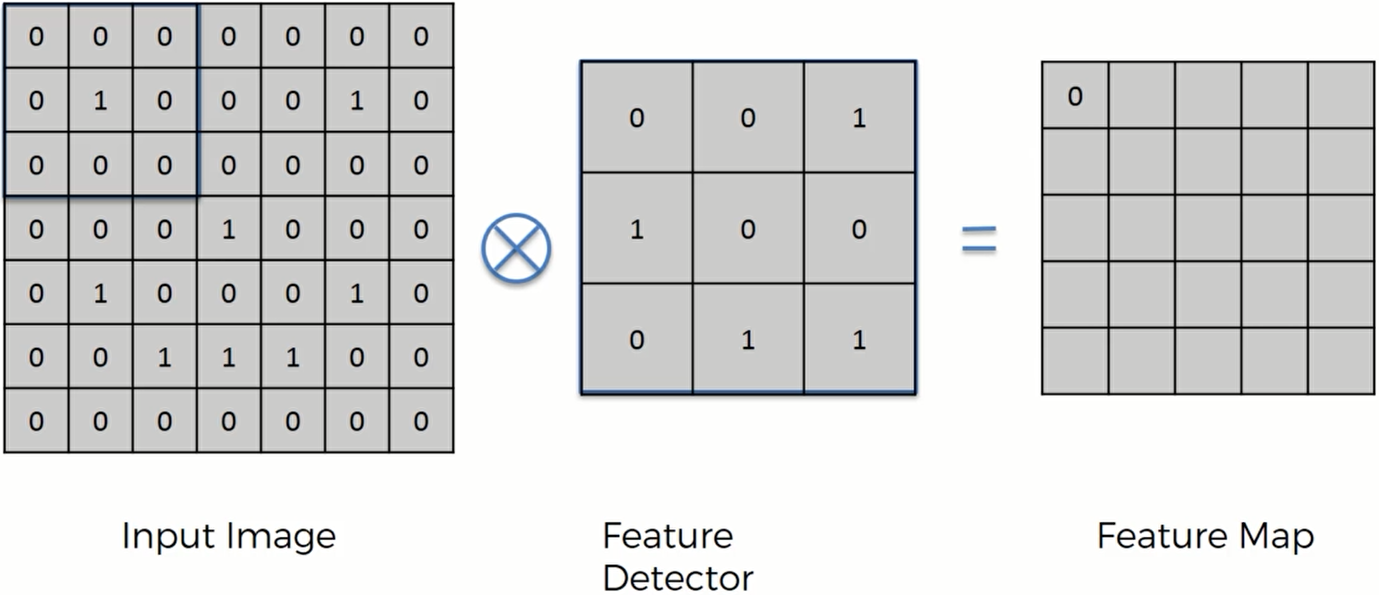
假设左边的矩阵是输入的图片,为了简化像素用01表示。中间的3x3矩阵叫做特征探测器,大多数卷积神经网络中用的都是3x3的矩阵,但是也有用5x5和7x7的。特征探测器和输入的图像矩阵做一个运算: 将特征探测器覆盖在图像矩阵的一片区域上,然后将这九个数相对应的一个值乘以一个值,计算过后特征探测器会向右移动,移动的距离叫做步长。最后计算九个数对应相乘的和
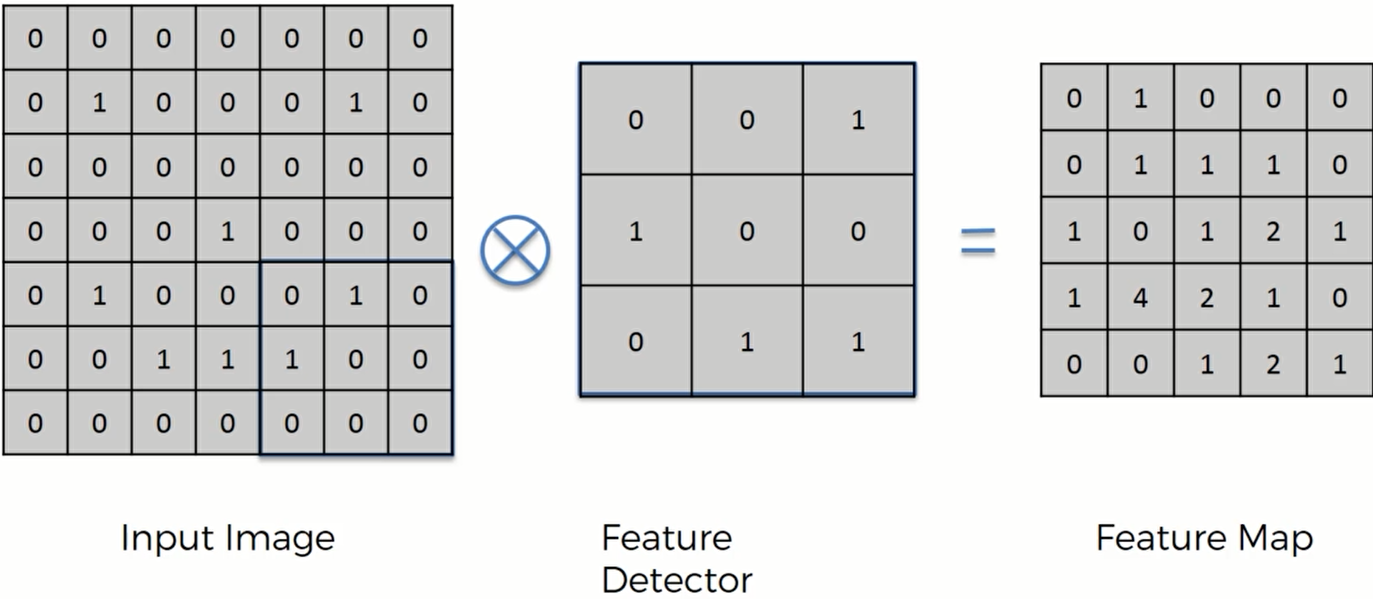
计算过后的矩阵如下:我们可以叫它 特征图或者Convolved Feature, 显然这个输入的矩阵被压缩了一点。这里我们用的步长是1(当步长为2的时候,得到的Feature Map就会进一步变小,通常2的效果更好)。
卷积过后,虽然矩阵中存储的数据变少了,但是特征探测器的目的是探测某些特征,也就是探测图像的某些完整部分。特征探测器具有某些特定的模式,而Feature map中数字最大的地方就是与探测器模式相匹配的地方。
这和我们大脑的工作模式相似,我们并不会一个一个像素看,而是看一些局部的特征。卷积也是这样,通过特征探测器在特征图中保留下有用的信息。
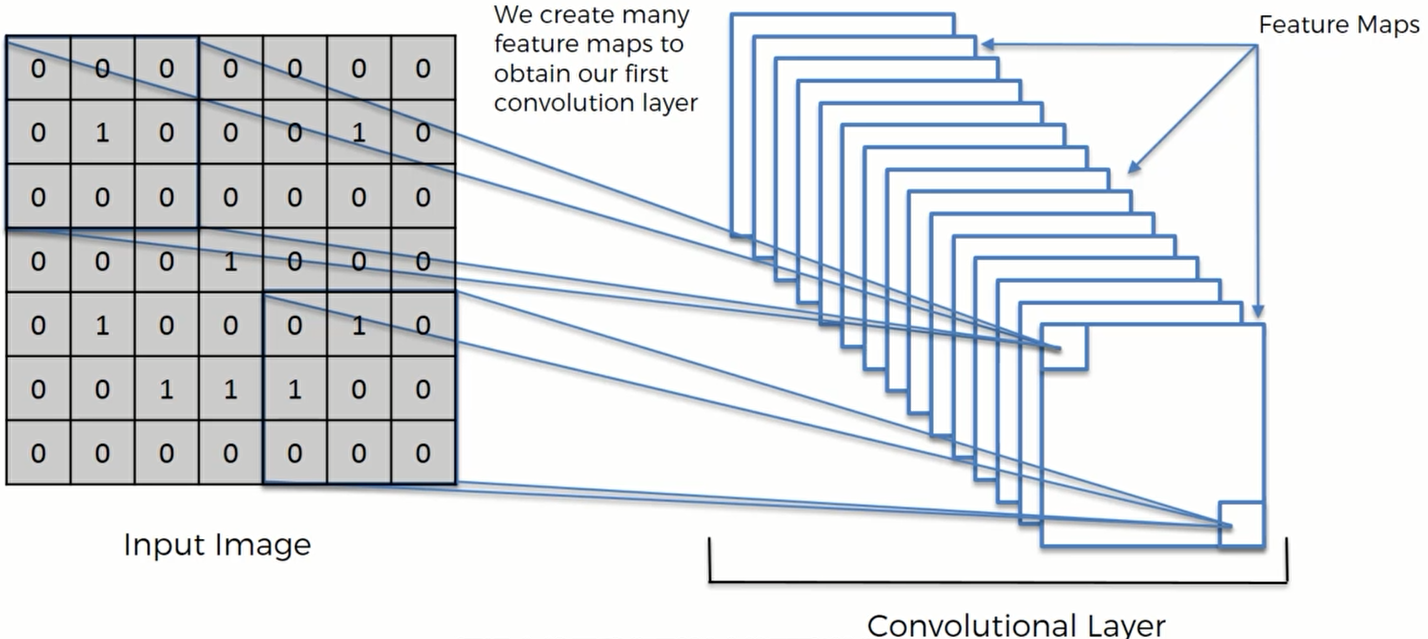
卷积过程中仅仅创建一张特征图是远远不够的。因为我们需要用到多个不同种类的特征探测器,所以需要创建多个特征图来保留图像中的信息。 然后,通过神经网络的训练,来决定哪个特征对于某个分类特别重要。
特征探测在滤镜/美化图片当中有广泛的应用,比如说对于这张泰姬陵的照片
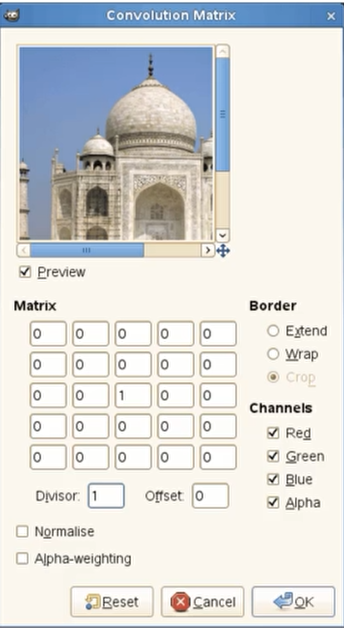
锐化
如果特征探测器是这样的,那么会对图像产生锐化的效果,照片会更加清晰:
因为这个探测器中间的数值是5,周围是-1,这个目的就是突触主体元素,而减少边缘周围的像素。

模糊
同样,模糊操作是一个 全部都是1的 探测器,这就说明了中间的像素和周围像素有着同等的重要性。他们合在一起就像是图片变模糊了一样

边界增强滤镜:

这个探测器只有-1和1,也就是说我们去掉了围绕中间主要元素周围的像素,只在左边保留一个-1。但是这个探测器的原理比较难以理解
边界探测滤镜:
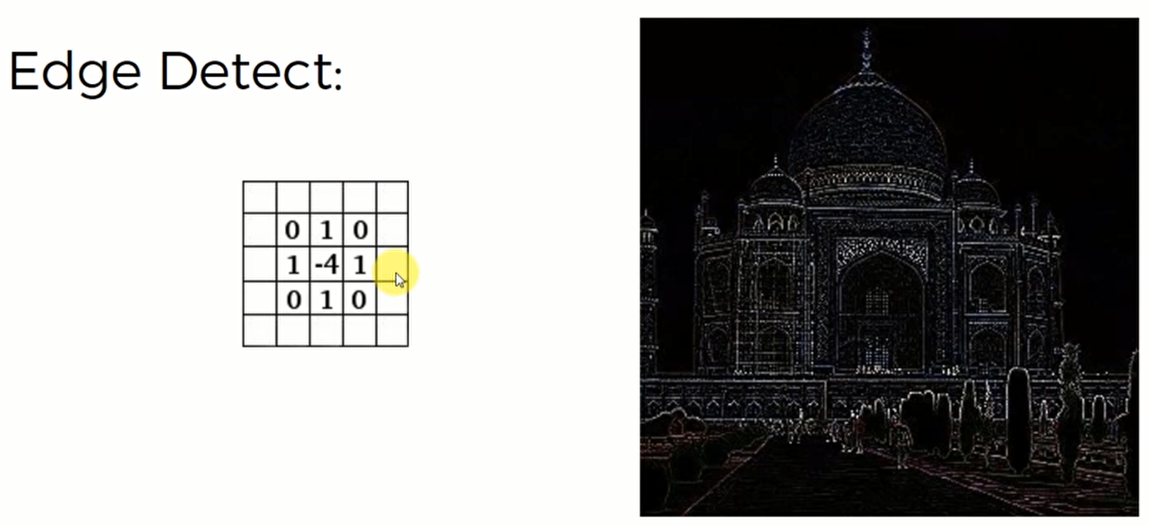
中间是4而上下左右是1,因此这个探测器削弱了中间主要元素的重要性,而提升了周围元素的重要性。这就期限了探测边框的效果
Emboss浮雕滤镜
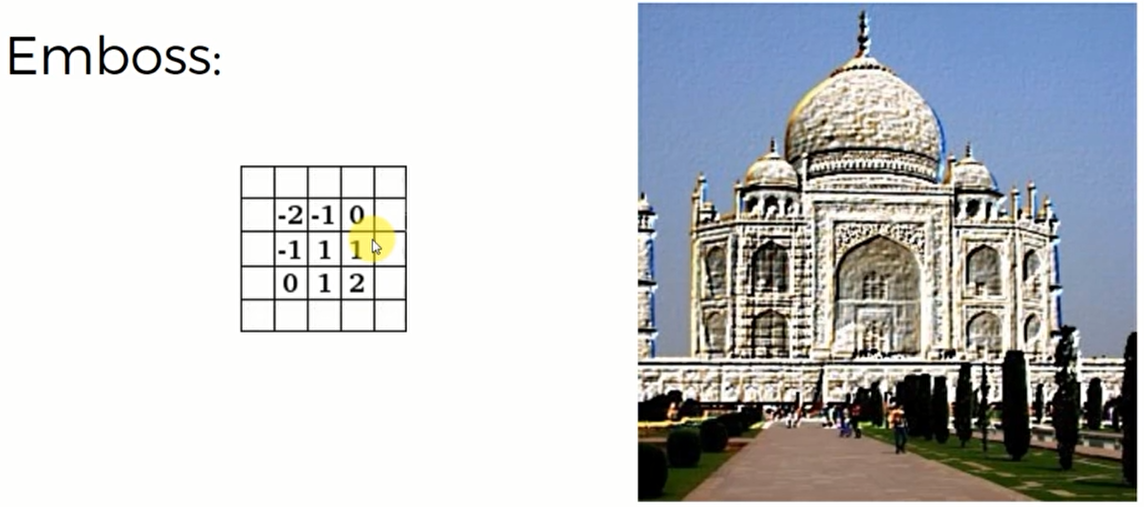
这个探测器,我们发现它是左右不对成的,因此体现在图片上也感觉到这个图片朝左凸出
ReLU Layer 线性整流函数
现在我们来介绍 ReLU,这是在卷积的基础上再添加的一个步骤
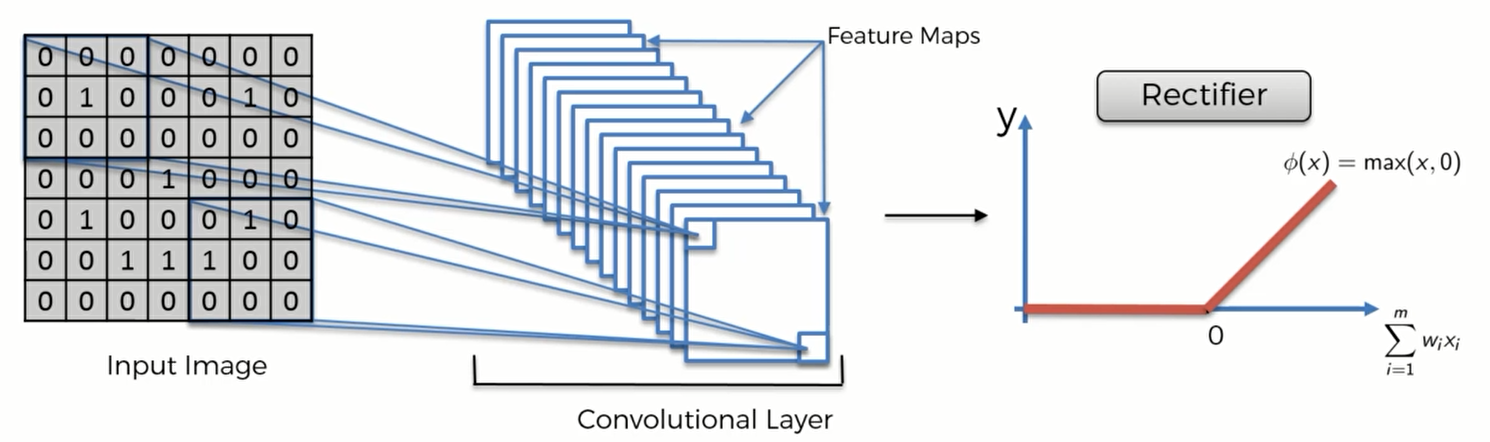
数据通过ReLU后,过滤掉负值,只会保留非负值,比如下面这幅图的效果:
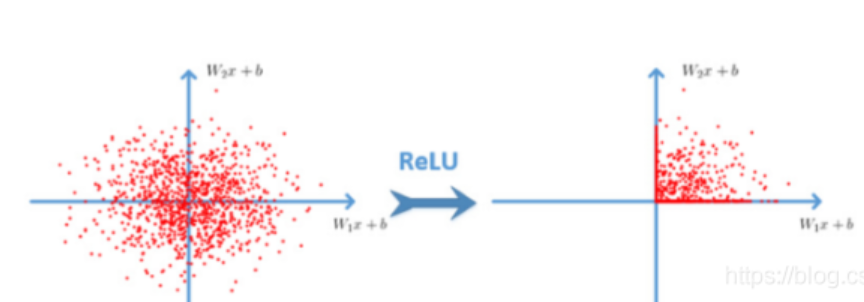
使用 ReLU的原因是它类似于一个过滤器,能打破神经网络的线性,并提高图像里或者神经网络模型中的 非线性。那么为什么要提高非线性呢?因为图像通常是高度非线性的,当我们在识别相邻不同物体时,有不同的边界、不同的颜色,因此图像可能具有很多非线性的元素。但是当我们进行卷积操作去建立我们的特征图的时候,有可能会引进一些线性的东西。
下面是一个例子:

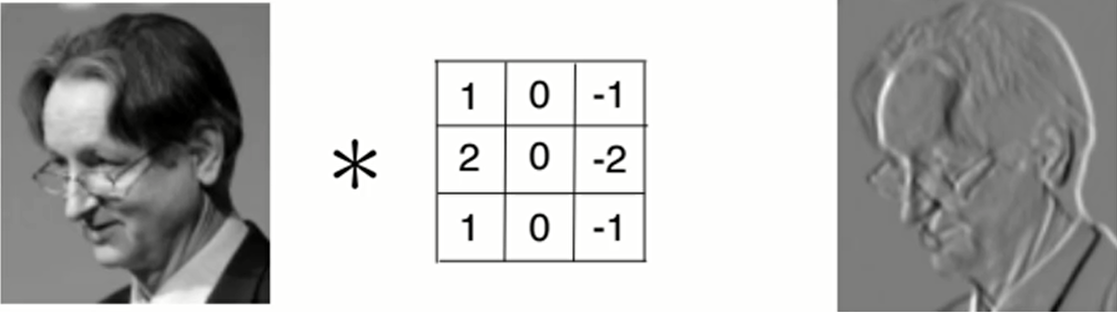
这张建筑物的图片,通过探测器处理之后变成了这样一张图片:

其中,黑色是负值而白色是正值。我们看到这幅图片中,白色到黑色之间是类似于线性变化的。但是我们再通过ReLU处理一下,就会得到这样一幅图片:

我们发现这样子的话这张图片就只有非负值了,白色和灰色之间没有一个渐变的阶段。
虽然我们现在还不能解释这样处理的好处,但是起码能给我们一个主观上的感受。
运用ReLU而不是Sigmoid函数,因为ReLU能有效解决梯度爆炸的问题,计算速度非常快(之所以计算快,因为relu函数公式的原因)
而之前的sigmoid函数的缺点:计算量相对大(公式$1/(1+e^{-z})$复杂),sigmoid函数反向传播时,很容易就会出现梯度爆炸现象
拓展阅读资料:
https://arxiv.org/pdf/1609.04112.pdf
https://arxiv.org/pdf/1502.01852.pdf
Max Pooling 最大池化
现在我们有好几张不同角度拍摄的猎豹的照片,我们怎么能让电脑在这几张不同的照片中识别出猎豹呢?

我们知道猎豹眼睛下方的“黑色泪痕”是一个辨别猎豹最明显的标志。但是如果电脑说必须在特定的位置,有特定的形状纹理才能识别到这个特征,那恐怕连一张照片都识别不了。所以我们必须确定我们的神经网络拥有一个空间不变性(spatial invariance’)的特性,这代表着电脑不用关心这个特征位于哪里,在图像的哪个位置。因为我们在制作特征图和制作卷积层的时候已经将这种情况考虑进去了。电脑也不需要关心采集到的特征是否有一些倾斜是否在纹理上有不同。所以我们的神经网络必须要有一些弹性,能够找到这种特征,这就是池化的作用

这就是最大池化的操作了。我们用一个 2x2的矩阵框在特征图上移动,然后每次选取矩阵框中最大的数字放在Pooled Feature Map当中,我们采用的步长是2.当然也可以选择1,只不过这样方框的位置和原来的位置就出现了重叠。这里超过了矩阵的边框也不要紧,只要记录下每个框中最大的数值即可。
经过最大池化,我们还是能够保留特征——那些最大值就是非常明显的特征,同时我们删除了75%不是明显特征的信息,减少了数据规模,防止出现信息过度拟合。更重要的是,我们保留了明显的特征,因此我们的算法可以允许一些图片的失真或者扭曲。
比如说对猎豹的泪痕花纹,假设这个花纹在特征探测是获得的数字是4. 那么,如果图像扭曲了,4出现了移位,只要和之前在同一个矩阵框之下,在池化后都能被记录下来。
问题: 池化有很多种,还有最小池化、平均池化 ,对于不同的池化方法,我们可以读者一篇论文
http://ais.uni-bonn.de/papers/icann2010_maxpool.pdf
经过最大池化,现在的模型如下:
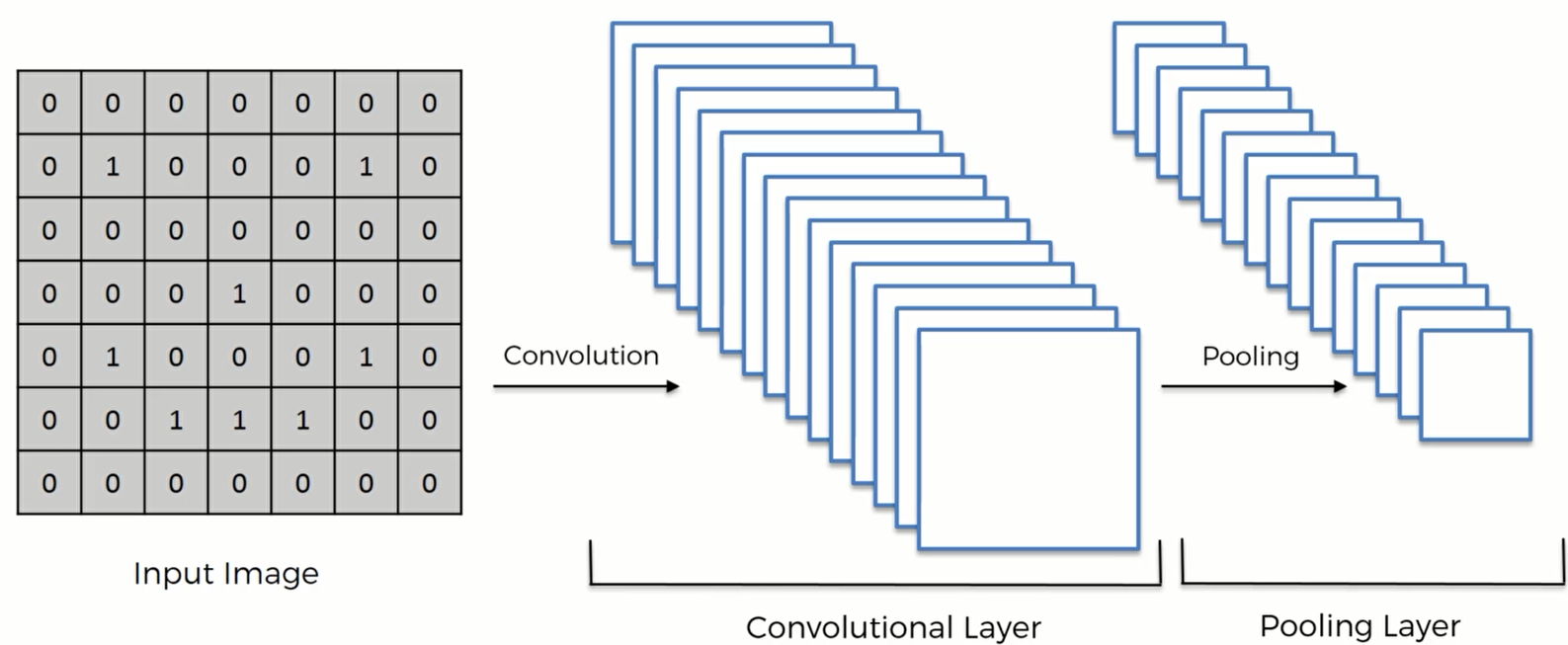
我们可以在这个网站上 http://scs.ryerson.ca/~aharley/vis/conv/flat.html 感受到池化带给我们的直观感受

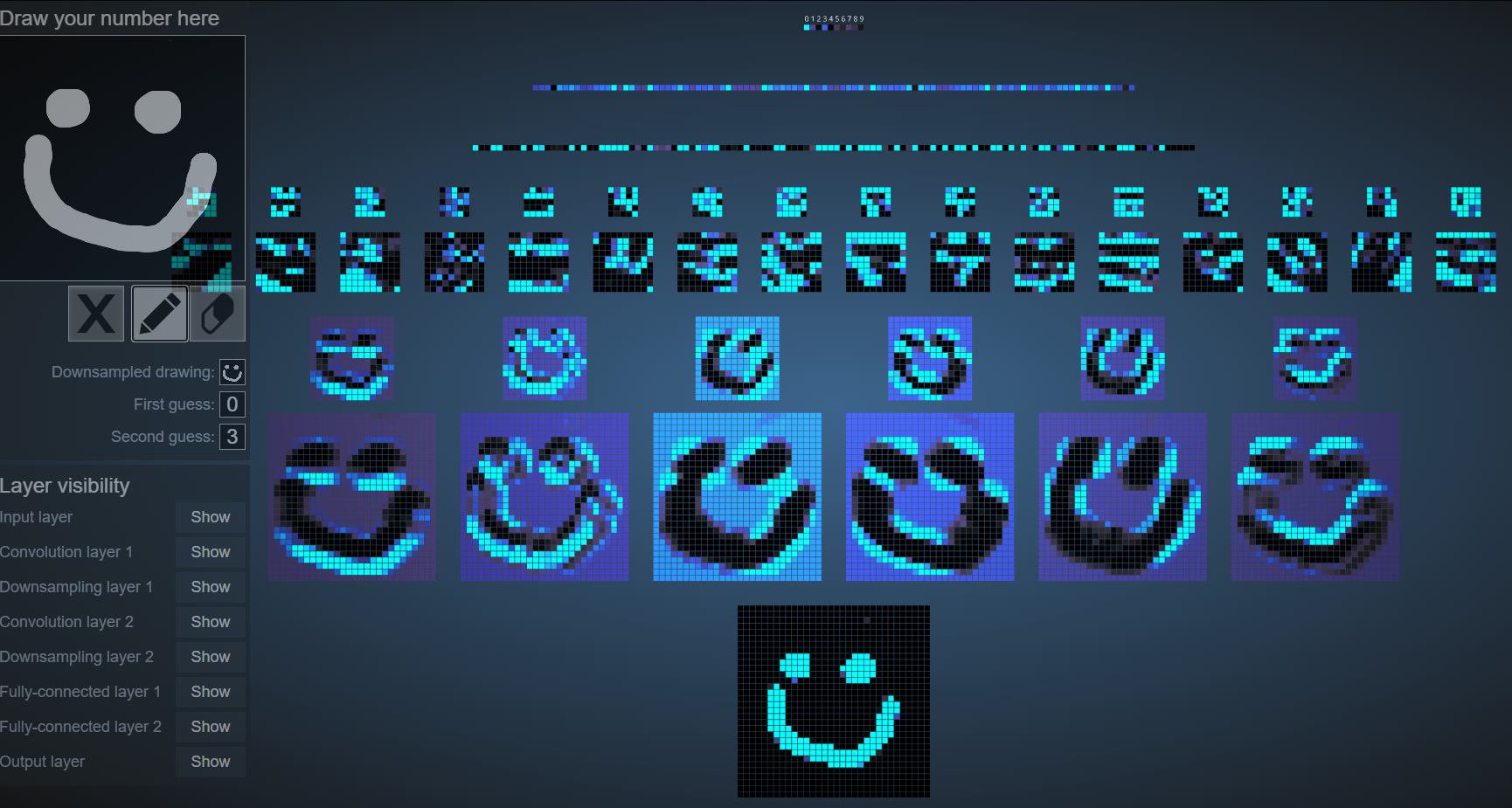
当我在左边输入8的时候,整个输入、卷积、池化、全连接的过程就在右边可视化了出来
最底下一层是我们的输入层
倒数第二层是第一次的卷积操作
倒数第三层是第一次的池化操作,我们发现经过了池化操作,图画变小了但是基本的特征还是保留了下来。
接着两层是第二次的卷积和池化,最上面是两次的全连接层,最后输出预测结果。
我们将8稍稍向右倾斜,发现得到的池化结果还是相似的。这就说明池化能让神经网络的弹性更大。
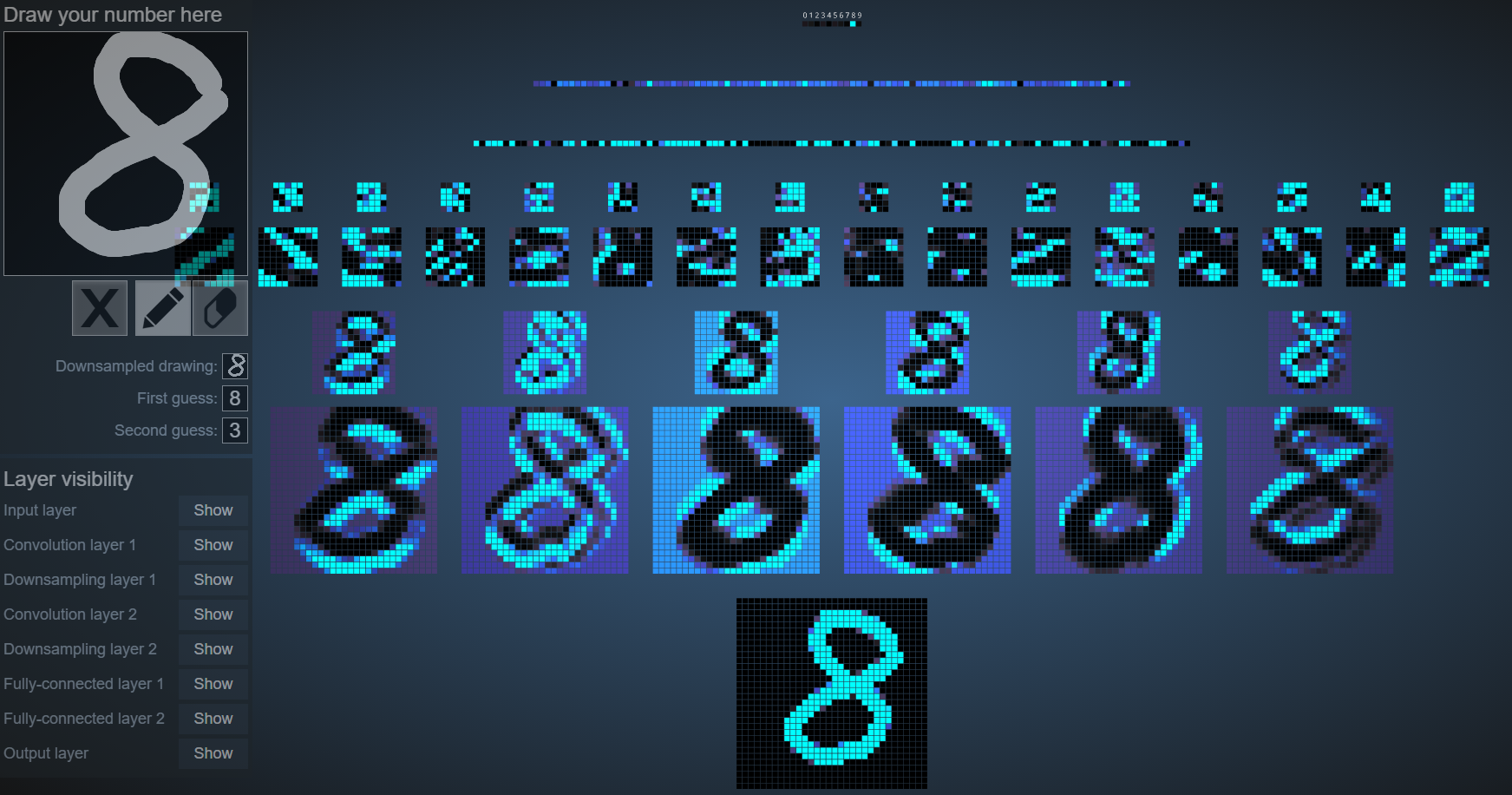
但是当我们画一个笑脸,我们会发现这个神经网络是识别不出这是一个笑脸的。因为显然它只被0-9训练过,对其他的输入是一无所知的。这就好比我们看到了一件我们从来没看到过的东西,我们会说:这个东西比较像XXX(一个我们认识的东西)
Flattening
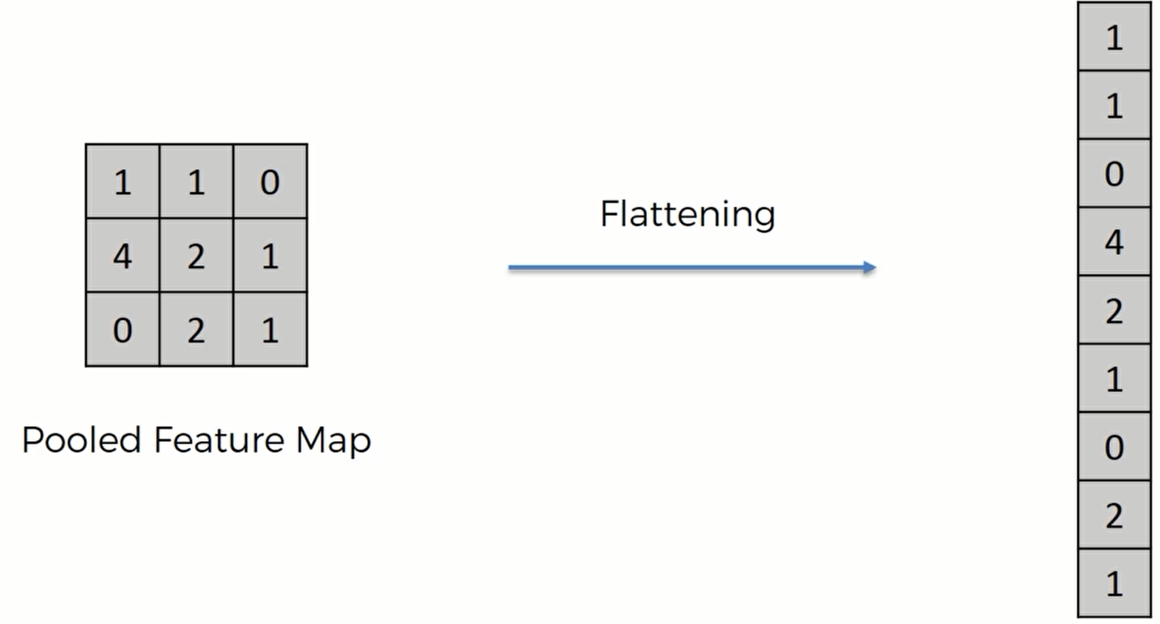
Flattening 操作非常简单,对于池化后的矩阵,我们只需要将其压平成一列即可。
那么,生成多个特征图放进卷积层,再通过ReLU函数来生成池化层,最后压平放入一个长向量里,这个长向量就是神经网络的一个输入层。
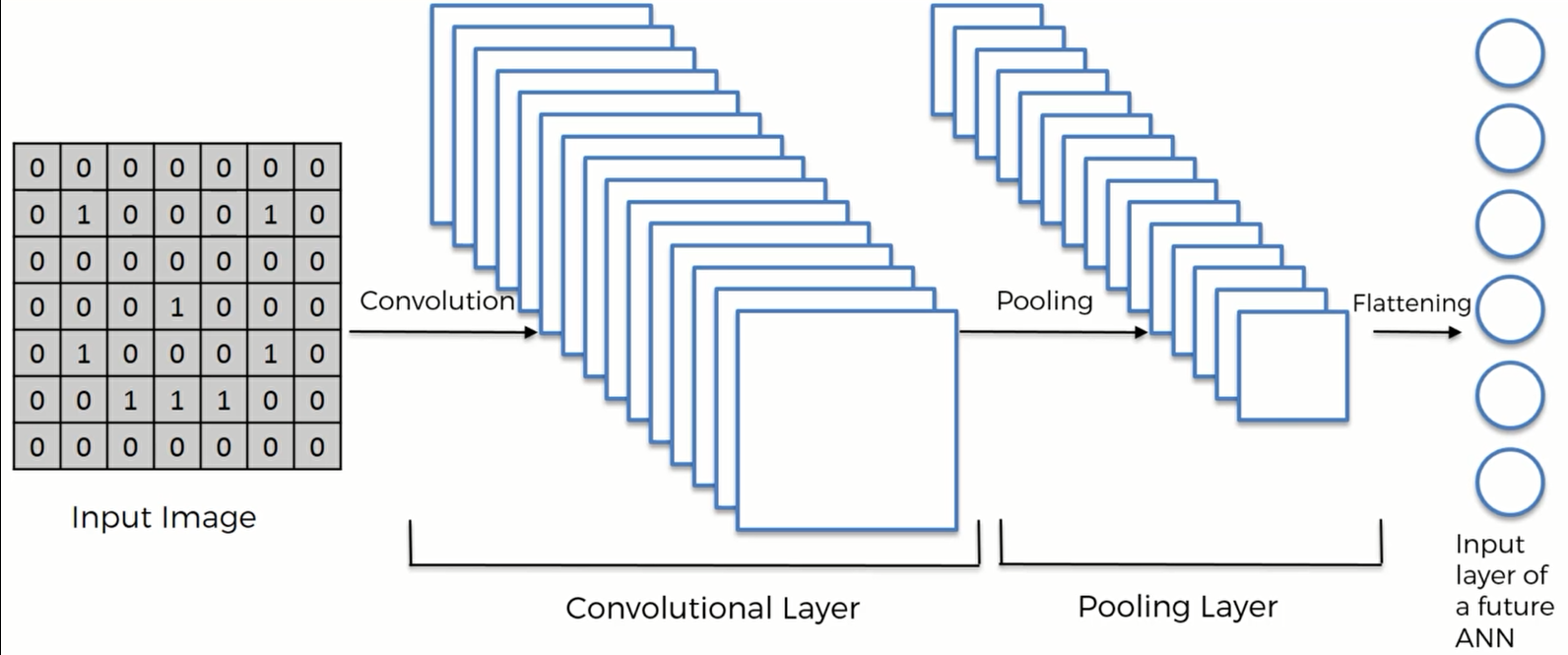
Full Connection
这一步我们将把整个ANN加到CNN一系列操作之后,如图所示:
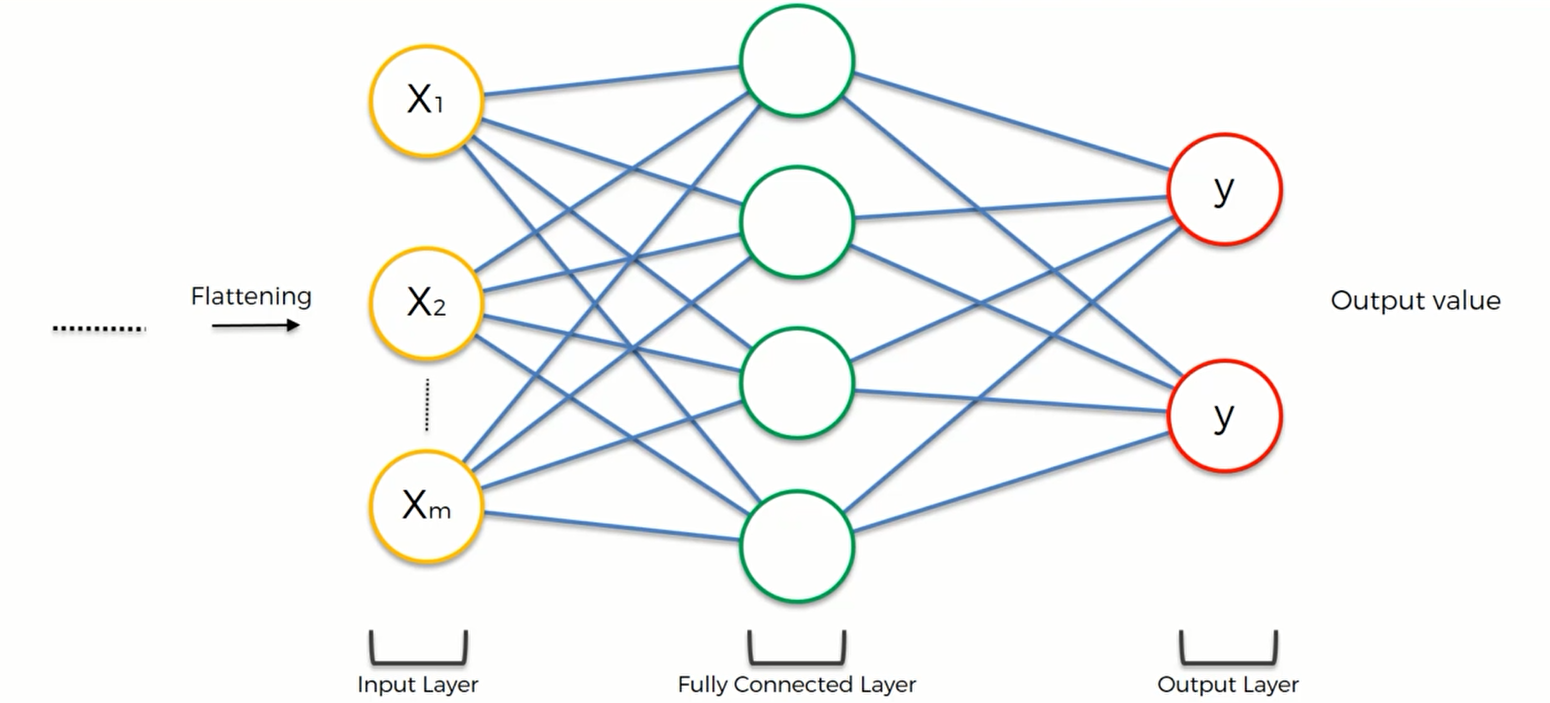
我们看到之前ANN中的隐藏层现在变成了一个全连接层。全连接层是一种特别的隐藏层,因为它和输入层还有输出层是全连接的。而一般的隐藏层并不这么干。
这里神经网络的主要目的是:它能把我们得到的特征加入更多的属性,以得到更好的预测结果。我们之前已经有了平坦化之后的输出向量,在那个向量里已经蕴含了一些特征,比如对照片进行一个分类操作,但与此同时我们知道ANN能够对特征进行一个推理和分析并发现新的属性,那我们为何不利用ANN这种功能来优化这些特征呢?
下面是一个更加复杂的例子,通过对这个例子的分析,我们会对CNN有更加深刻的理解:
在这个模型当中我们有两层全连接层,并且有两个输出神经元(狗和猫)。我们知道在ANN当中只有一个输出神经元,那在CNN中为什么要有两个神经元呢?事实上,如果分成两类的话,我们可以用一个二元的输出神经元:0代表狗,1代表猫。但是如果要分类的东西较多,比如说还有鸟,大象之类的动物,那就必须给每一个动物都分配一个输出神经元。这是CNN 的特性。
图像经过卷积池化平坦化后的数据被输入到ANN当中,然后通过一个损失函数(交叉熵函数)计算误差,这个误差是用来衡量神经网络的性能的。计算出误差以后我们将误差往回传播并调整一些参数:比如说这些神经网络中的权重和卷积过程中的特征探测器。因为很可能一开始的特征探测器是错误的,因此调整特征探测器能提高预测的准确性。经过调整后,再将信息传递到ANN当中,并计算误差,返回调整。以此进行多轮学习,最终我们的神经网络会得到优化。
这个过程和ANN是一样的,只是需要的时间更长一点,因为多了之前的三个步骤(卷积池化压平)
那么这两个输出神经元是如何工作的呢?
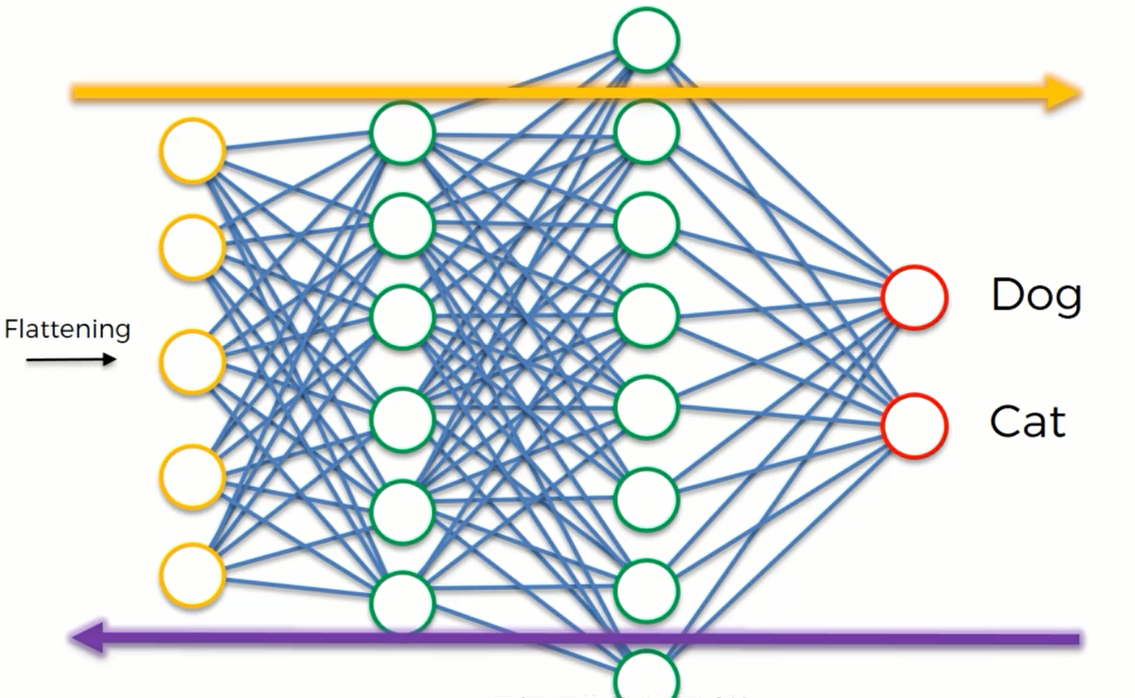
我们先从狗开始,我们首先要做的就是找到哪些权重杯赋予与“狗”神经元相连接的突触。这样我们就可以知道那个神经元对”狗”重要。为了方便,我们把值设置为0-1之间,如果这个神经元是0.9、1,那么就说明这个神经元被激活了,它认为它找到了某个特征;0就代表这个神经元没有找到特征。这些神经元的值将会传给Dog和Cat这两个输出神经元,然后由Dog和Cat神经元负责去判断这个特征是否符合它的要求。
比如说这里,第一、二、六个神经元被激活了,它们分别代表狗的耳朵,鼻子和舌头。那么在训练的时候狗神经元就知道这些特征是属于狗的,经过多次迭代,狗神经元在预测的时候就会认为如果这些神经元都激活了,那么这张图片就应该属于狗,因此狗神经元就会被激活。而猫神经元就会认为这些隐藏层的神经元被激活时,图像中的动物并不是猫,久而久之,猫神经元就会忽略这些神经元的信号。
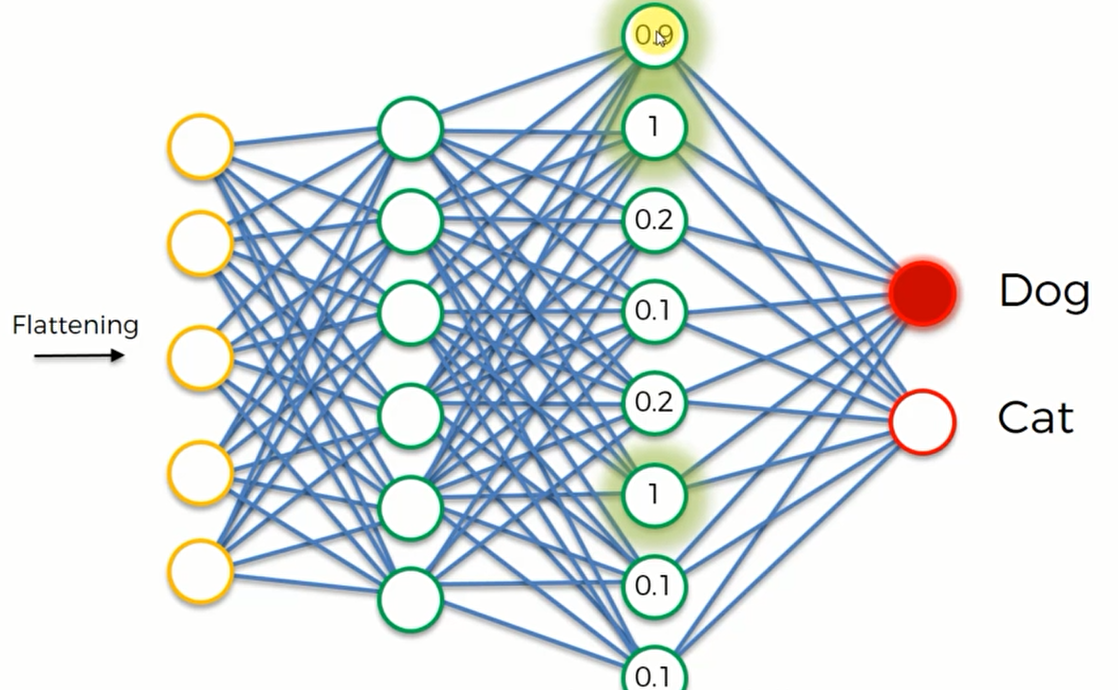
同理,对猫来说也有“属于”它的神经元,而狗神经元就会选择忽视那些属于猫特征的神经元。
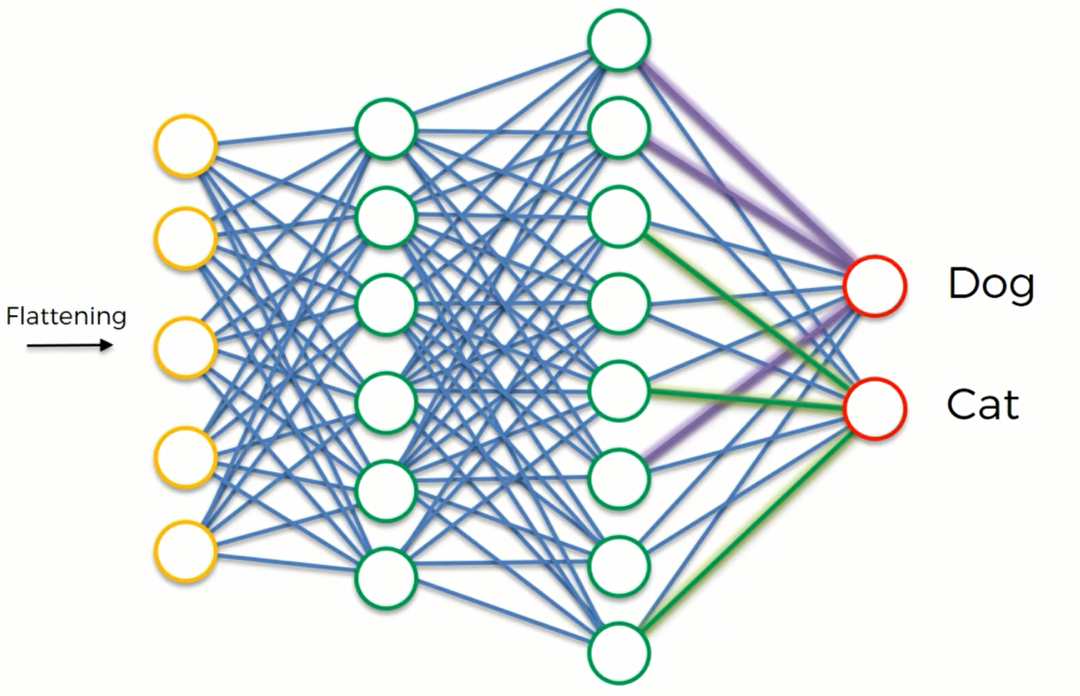
经过成千上百次的训练,CNN就会自己判断这张图片是属于猫还是属于狗了,如下图所示
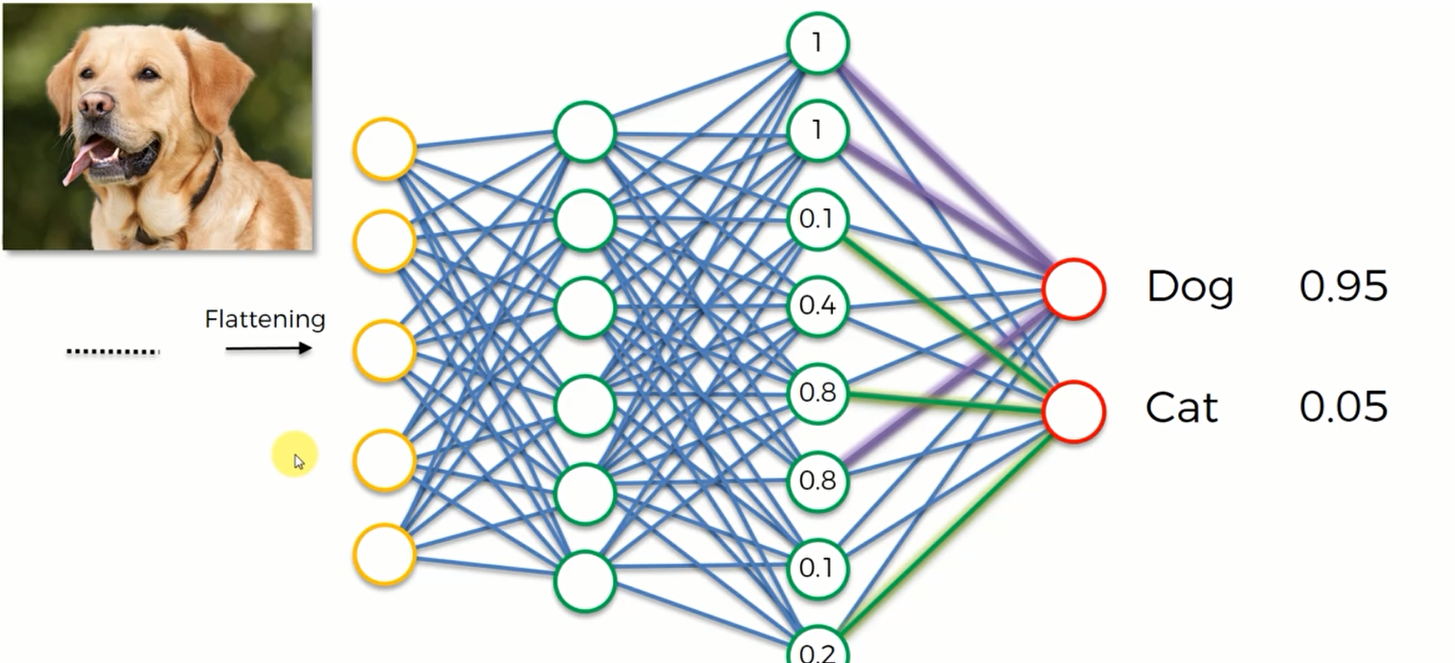
这时候我输入一张狗的照片,要CNN帮我们预测分类。他们会通过倾听全连接层传递的信息而进行判断并给出可能是狗的概率和可能是猫的概率。概率是由全连接层的神经元根据他们的值 “投票”产生的 ,这就是全连接网络的工作原理。
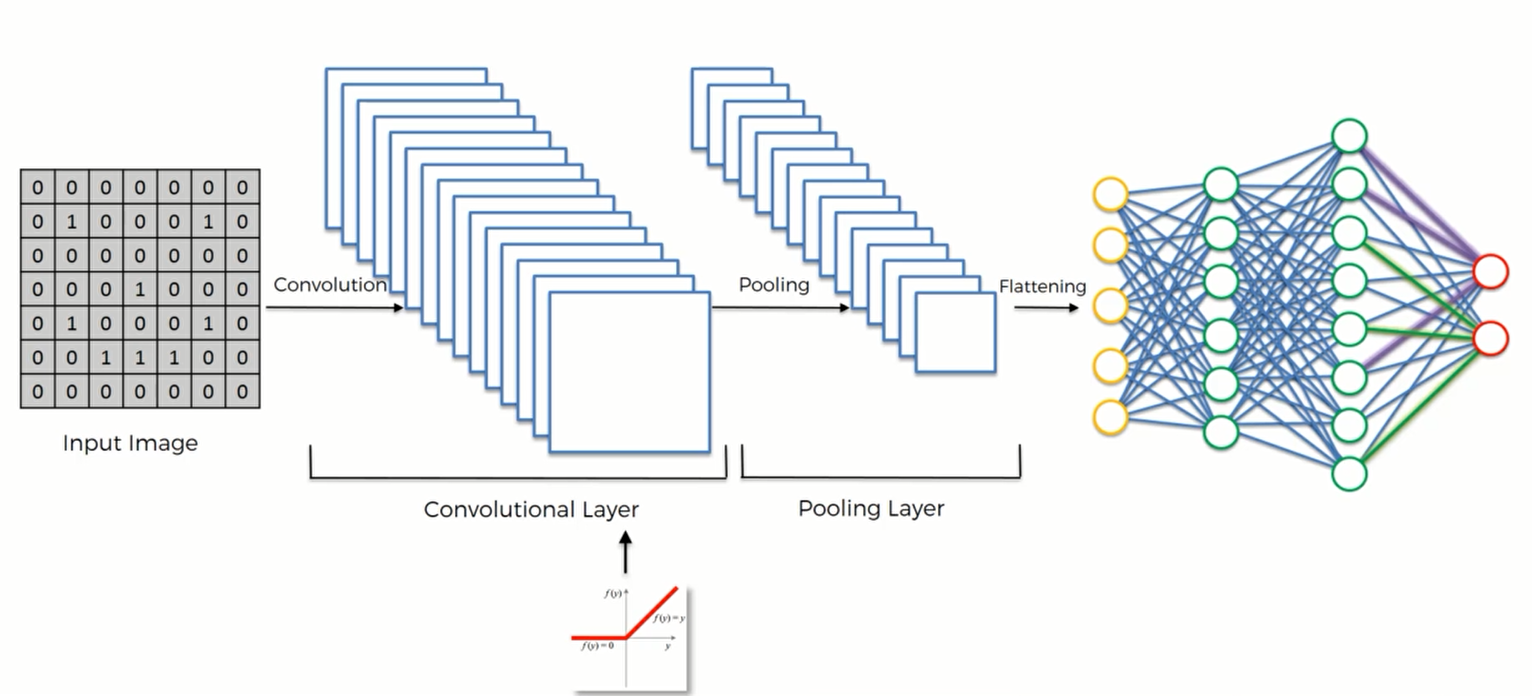
整一个CNN的过程可以用下图总结
学习博客: