Optimal BST
什么是最优二叉搜索树?
假设我们在设计一个实现英语到法语的翻译,对英语文本中出现的每个单词查找对应的法语单词。
为了实现这个操作,我们可以创建一颗二叉搜索树,将n个英语单词作为关键词,对应的法语单词作为关联数据。
于对文本中的每个单词都要进行搜索, 我们希望花费在搜索上的总时间尽量少
我们知道平衡二叉搜索树或者红黑树的搜索时间是 $O(logn)$ 。但是,单词出现的频率是不同的。
像 “the” 这种频繁使用的单词有可能位于搜索树中远离根的位置上,搜索一次可能需要花费很多时间;而像 “machicolation” 这种很少使用的单词可能位于靠近根的位置上,搜索一次只要花很少的时间。
这样的结构会减慢翻译的速度, 因为在二叉树搜索树中搜索一个关键字需要访问的结点数等于包含关键字的结点的深度加1 , 我们希望文本中频繁出现的单词被置于靠近根的位置。更甚者,文本中的一些单词可能没有对应的法语单词,这些单词根本不应该出现在二叉搜索树中中。
于是我们定义:在给定单词出现频率的前提下,我们应该如何组织一颗二叉搜索树,使得所有搜索操作访问的结点总数最少,就是一个最优二叉搜索树问题。
抽象总结一下这个问题:
给定一个n个不同关键字已排序的序列$K=
有些要搜索的值可能不在k当中,因此我们还需要有n+1个”伪关键字” $d_0,d_1,\cdots d_n$ 表示不在K中的值:其中 $d_0$ 表示所有小于 $k_1$ 的值,$d_n$ 表示所有大于$k_n$ 的值,对 $i = 1,2,\cdots,n-1$ ,伪关键字 $d_i $ 表示所有在 $k_i$ 和 $k{i+1}$ 之间的值。对每个伪关键字 $d_i$ ,也都有一个概率p表示对应的搜索频率。这些结点是整个二叉树的叶子结点
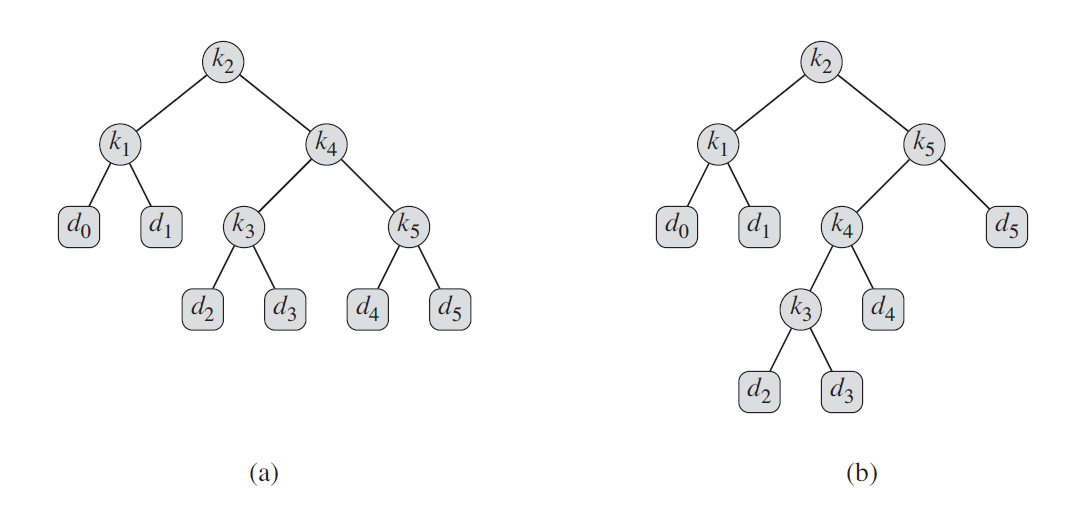
下图是对一个 n=5 个关键字的集合构造的两颗二叉搜索树。 每次搜索要么成功(找到关键字$k_i$),要么失败(找到某个伪关键字$d_i$)
因此 我们可以得到如下公式: $\sum{i=1}^n p_i+\sum{i=0}^n q_i = 1$
对于 $p_i$ 和$q_i$ 的搜索概率如下:

由于我们知道每个关键字和伪关键字的搜索概率,因而可以确定一颗给定的二叉搜索树T中进行一次搜索的期望代价
假定一次搜索的代价等于访问的节点数,即此次搜索找到的结点在T中的深度再加1,那么计算公式如下:
$E[T中搜索代价] = \sum{i=1}^n(depth_T(k_i)+1)*p_i+\sum{i=0}^n(depth_T(d_i)+1)*q_i$
从这个公式我们可以算出,上图(a)树的期望搜索代价为2.80,而(b)树的期望搜索代价为2.75
那么对于一个给定的概率集合,我们希望构造一棵期望搜索代价最小的二叉树,称之为最优二叉搜索树。对于上面这组概率来说,最优二叉搜索树是 (b)树。
因此可见最优二叉搜索树并不一定是最矮的(b比a高),而且概率最高的关键字也并不一定出现在二叉搜索树的根节点(概率最高应该是k5而最优二叉搜索树的根节点是$k_2$)。
关于这个问题,我们如果通过穷举法,肯定是不行的,因此我们采用动态规划的方法来求解:
动态规划方法求解
最优二叉搜索树的最优解
给定关键字序列 $ki,\cdots,k_j$,其中某个关键字,比如说 $k_r(i\leq r\leq j)$, 是这些关键字的最优子树的根节点。那么 $k_r$ 的左子树就包含关键字 $k_i,\cdots,k{r-1}$和伪关键字($d{i-1},\cdots,d{r-1}$) ;同理右子树包含关键字 $k{r+1},\cdots ,k_j$ 和伪关键字 ($d_r,\cdots,d_j$). 只要我们检查所有可能的根节点 $k_r(i\leq r\leq j)$,并对每种情况分别求包含 $k_i,\cdots,k{r-1}$ 以及包含$k_{r+1},\cdots ,k_j$ 的最优二叉搜索树,即可保证找到原问题的最优解。
递归算法
我们定义 $e[i,j]$ 为在包含关键字 $k_i,\cdots,k_j$ 的最优二叉搜索树中进行一次搜索的期望代价。最终我们希望计算出 $e[1,n]$
当 $j\geq i$ 的时候,我们需要从 $ki,\cdots,k_j$中选择一个根节点 $k_r$ ,然后构造一颗包含关键字 $k_i,\cdots,k{r-1}$ 的最优二叉搜索树作为其左子树,以及一颗包含关键字 $k_{r+1},\cdots,k_j$ 的二叉搜索树作为其右子树。
由于当一颗子树成为一个结点的字数时,期望搜索代价的增加值应为所有的概率之和,因此对于包含关键字 $ki,\cdots,k_j$ 的子树,所有概率之和为 $w(i,j) = \sum{l=i}^jpl+\sum{l=i-1}^jq_l$
因此,若 $k_r$ 为包含关键字 $k_i,\cdots,k_j$ 的最优二叉搜索树的根节点,我们有如下公式
$e[i,j] = p_r+(e[i,r-1]+w(i,r-1))+(e[r+1,j]+w(r+1,j))$
又因为 $w(i,j) = w(i,r-1)+p_r+w(r+1,j)$
因此$e[i,j]$ 可以重写为 $e[i,j]=e[i,r-1]+e[r+1,j]+w(i,j)$
我们可以选取期望搜索代价最低者作为根节点,可以得到最终的递归公式
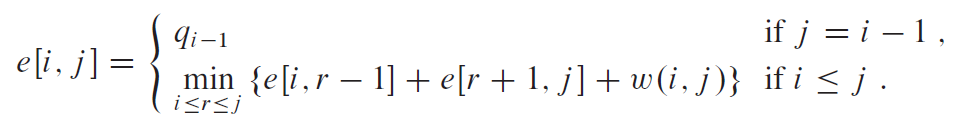
$e[i,j]$ 的值给出了最优二叉搜索树的期望搜索代价。为了记录最优二叉搜索树的结构,对于包含关键字 $k_i,\cdots,k_j(i\leq i\leq j\leq n)$ 的最优二叉搜索树,我们定义 $root[i,j]$ 保存根结点 $k_r$ 的下标r。
计算最优二叉搜索树的期望搜索代价