最大流

Posted on
Words count in article: 2.9k | Reading time ≈ 11

最大流

基本概念

无论是电网、水管网、还是其他地一些网络，他们都有一个共同点：网络传输都有方向 和 容量。设有带权图 $G=(V,E) , V={s,v_1,v_2,v_3,\cdots,t}$ 。 在图G中有两个特殊的点s和t，s称为源点，t称为汇点。图中各边地方向表示允许的流向，边上地权值表示该边允许通过的最大可能流量cap，且$cap\geq 0$ 称为边地容量。而且如果边集合E含有一条边$(u,v)$,必然不存在反向的平行边$(v,u)$,称这样的有向带权图为网络。 因为如果存在可以直接合并掉。

现在有一家公司想要从工厂s运往仓库t，找到一家代理公司。代理公司安排了若干货车和运输线路，中间要经过若干城市，边上的数值代表两个城市之间每天最多运送产品的数量。

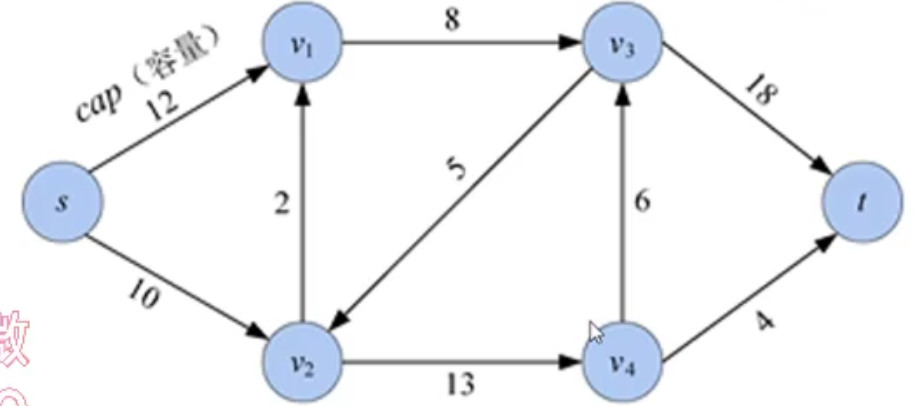
这就类似一个地下水管网络，我们看不到水在地下管道内是怎么流动的，但是直到从进水口流进多少水，就会从出水口流出来多少水。

网络流

网络流即网络上的流，是定义在网络边集E上的一个非负函数$flow={flow(u,v)}$, flow(u,v)是边上的流量

可行流：

满足以下两个性质的网络流flow称为可行流

我们要从s将货物运送到t，需要满足几个条件

  1. 容量约束，每个管道的实际流量 flow 不能超过该管道的最大容量 cap
  2. 流量守恒，除了源点是全部汇出没有汇入、汇点是全部汇入没有汇出的，其他中间节点流入和流出的量都是一模一样的，不允许中间节点有存货

源点s：

源点主要是流出，但也有可能流入，例如货物运出后检测出的一些不合格产品需要返厂，这对源点来说就是流入量。因此，源点的净流出值f=流出量之和-流入量之和。即： $f=\sum{(s,x)\in E}flow(s,x)-\sum{(y,s)\in E}flow(y,s)$

从下图也可以反映出流量守恒和容量约束

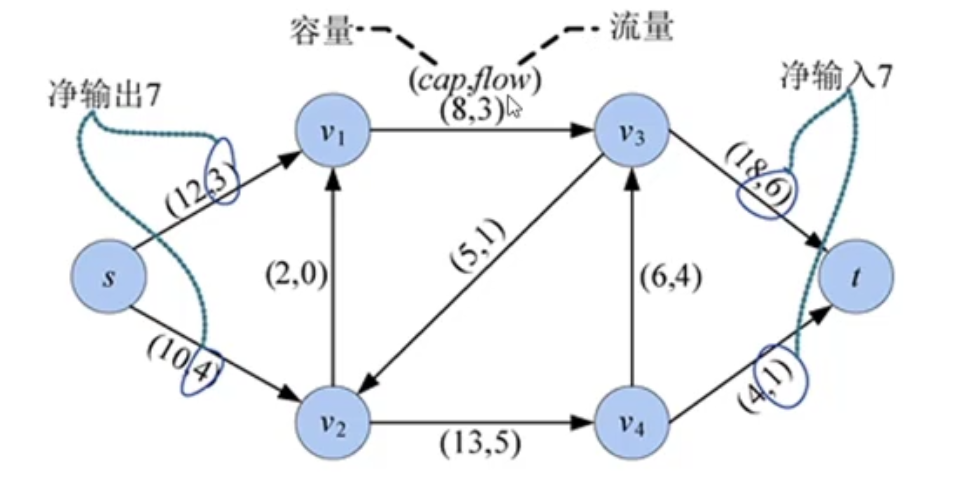
现在我们提出网络最大流问题：在满足容量约束和流量守恒的前提下，在流网络中找到一个净输出最大的网络流。

我们先来学习 Ford&Fullkerson提出的方法。该方法的基本思想是在残余网络中找可增广路，然后在实流网络中沿可增广路增流，直到不存在可增广路为止。这里要注意，找可增广路的方法有很多。

残余网络：

每个网络G及其上的一个流flow，都对应一个残余网络G*.G* 和 G结点集相同，而网络G中的每条边对应G*中的一条边或者两条边。在残余网络中，与网络边对应的同向边是可增量(即还可以增加多少流量)，反向边是实际流量

那么我们可以根据原来的图来画出残余网络

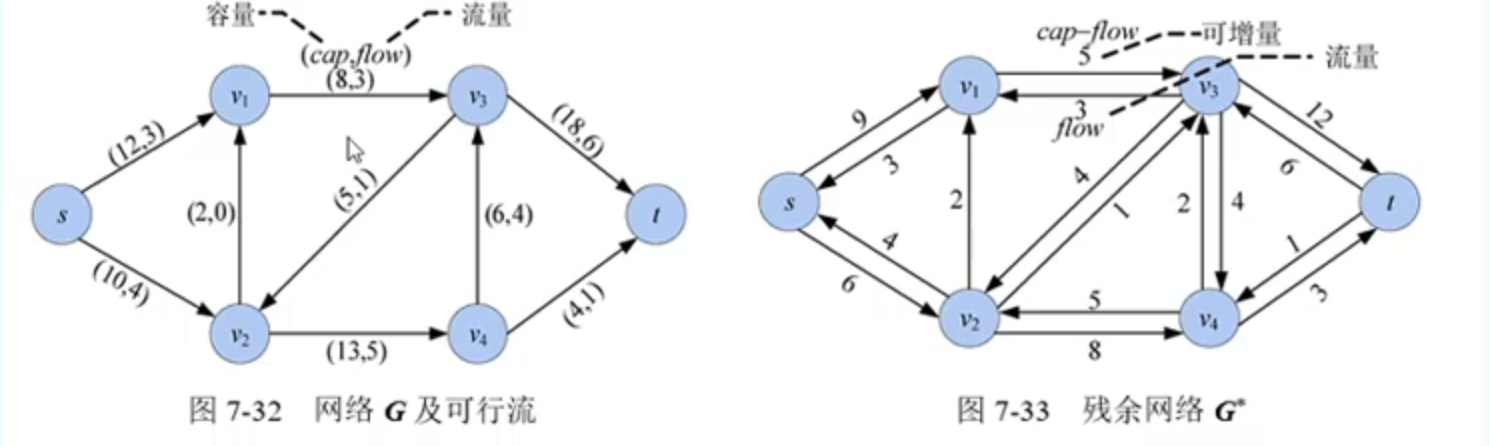
可增广路：

是残余网络G* 中一条从源点s到汇点t的简单路径。例如：$s-v_1-v_3-t$ 就是一条可增广路。如下图

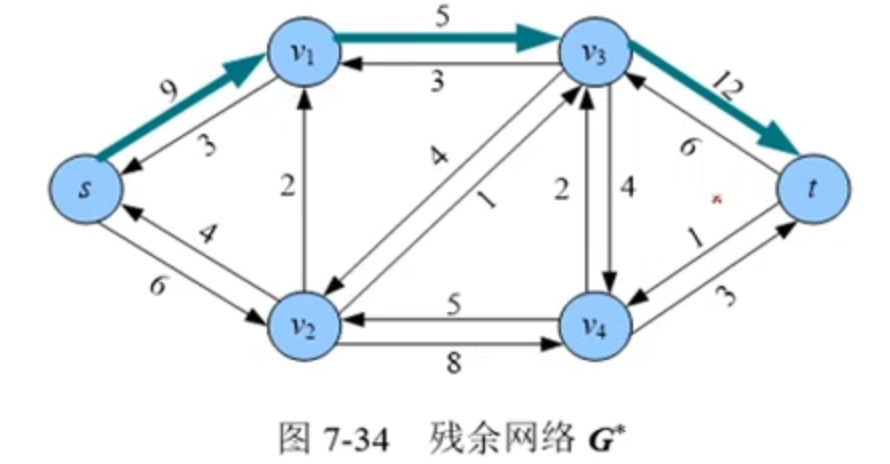
然后我们可以沿着增广路径来增加我们的货物数量。但是注意这里增加的量是路径上数值最小的路段。比如说这里能增加的量是5。在增加了货物数量之后，我们还需要修改增广路上的值。比如说这$s-v_1$从9改成4，$v_1-v_3$的线路被抹去，$v_3-t$的线路从12改为7.

可增广量

可增广量是指在可增广路p上每条边可以增加的流量最小值。求网络G的最大流，首先在残余网络中找可增广路，然后再实流网络G‘中沿可增广路增流，直到不存在可增广路为止。这是实流网络G’就是最大流网络。

可增广路增流

增流操作可以分为两个过程：一是在实流网络中增流，二是在残余网络中减流。因为残余网络中可增广路上的边值表示可增量，在实流网络中流量增加了，那么可增量就少了。

直接拿给我们一个残余网络，我们是不能判断哪一条是可增量哪一条是实际流量的

实流网络增流

在实流网络中沿着可增广路增流: 可增广路上同向边增加流量d，反向边减少流量d。

残余网络减流

在残余网络中沿着可增广路减流：可增广路上的同向边减少流量d，反向边增加流量d

增广路算法

增广路定理 ：设flow是网络G的一个可行流，如果不存在从源点s到汇点t关于flow的可增广路p，则flow是G的一个最大流

增广路算法： 增广路算法的基本思想是在残余网络中找到可增广路，然后在实流网络中沿着可增广路增流，在残余网络中沿可增广路减流；继续在残余网络中找可增广路，知道不存在可增广路为止。此时实流网络中的可行流就是所求的最大流。

最短增广路算法

如何找到一条可增广路呢？我们可以设置最大容量优先，也可以是最短路径(广度优先)优先。 Edmonds-Karp算法就是以广度优先的增广路算法，又称为最短增广路算法(Shortest Augument Path, SAP)

步骤

  1. 初始化可行流 flow为零流，$vis[]$数组为$false$，$pre[]$数组为-1,vis数组代表该节点是否已经访问过，pre数组代表该节点的前驱结点
  2. 令$vis[s] = true$,并将s加入队列q
  3. 如果队列不空，就继续下一步，否则算法结束，并返回最大流
  4. 队头元素new出队，在残余网络中检查new的所有邻接结点i。 如果i未被访问，那么就访问i结点并令 $vis[i]=true,pre[i] = new$。 如果 $i=t$ ，说明已经到达汇点，找到一条可增广路，转向第（5） 步；否则结点i加入队列q，转向第3步。
  5. 从汇点开始，通过前驱数组$pre[]$ ，逆向找可增广路上每条边值的最小值，即可增量d。
  6. 在实流网络中增流，在残余网络中减流，$Maxflow+=d$ ，并转向第(2)步

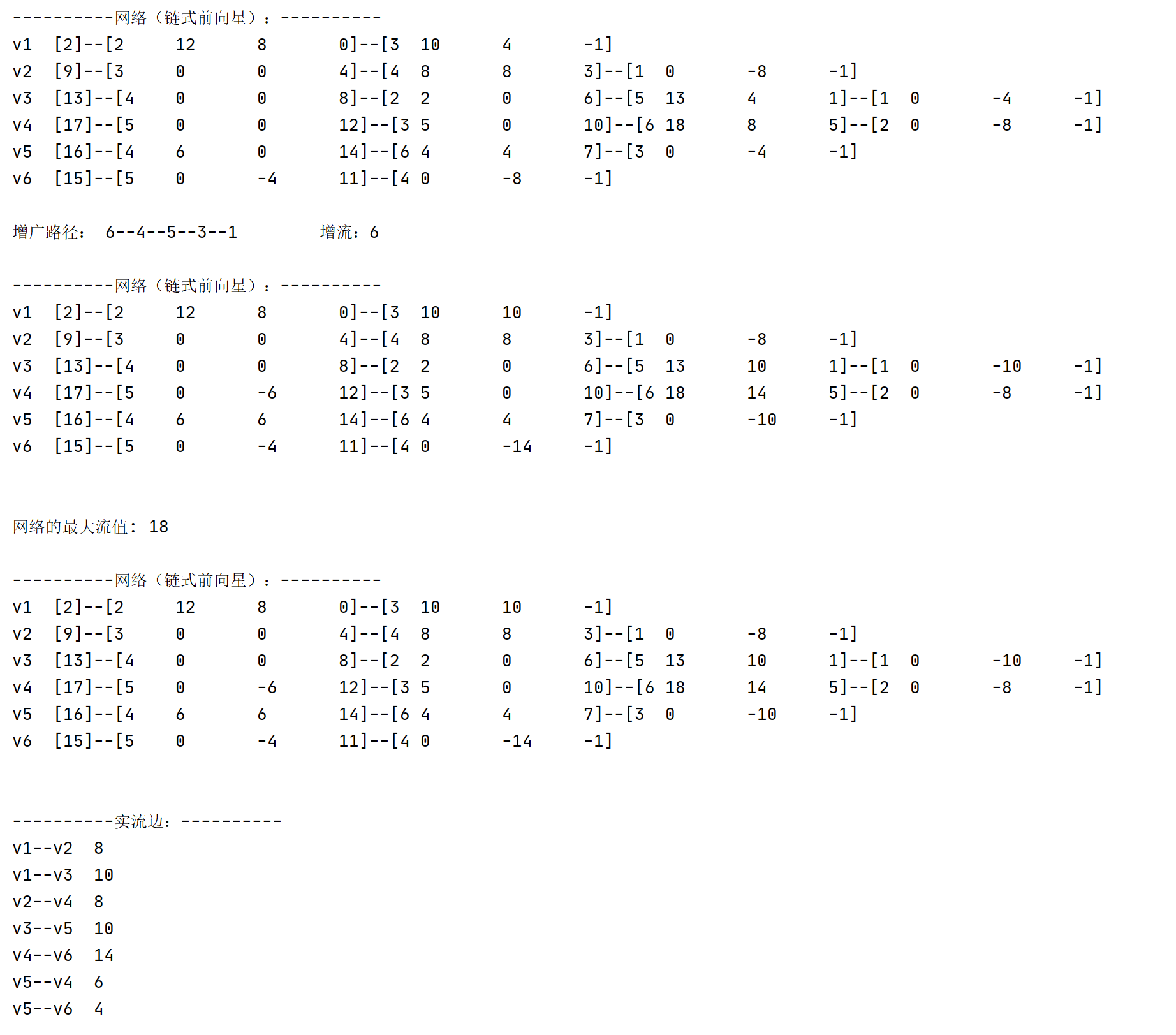
比如说这个图，我们可以先来手工计算改图的最大流。

时间复杂度

从算法的描述中可以看出，找到一条可增广路的时间是 $O(E)$,最多会执行 $O(VE)$次，因为关键边的总数为$O(VE)$.因此总的时间复杂度为 $O(VE^2)$ ，其中 V为结点个数，E为边的数量

空间复杂度：

使用了一个二维数组表示实流网络，因此空间复杂度为 $O(V^2)$

代码剖析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
   #include<bits/stdc++.h>
using namespace std;
/*首先我们定义一些常量，N代表结点数，M代表边数*/
const int inf = 0x3f3f3f3f;
const int N = 100;
const int M = 10000;
int cnt,d;
/*然后我们定义head数组(链式前向星需要)，前驱数组，和是否已访问的标志数组*/
int head[N],pre[N];
bool vis[N];
/*接下来我们定义链式前向星，并对head数组初始化为-1，但是这个链式前向星还需要包含两个数据
分别是边的容量和流量
*/
struct Edge{
    int v,next;// v代表除了head之外的另一个结点，next指的是下一条边的序号
    int cap,flow; 	
}E[M];

void init(){
    memset(head,-1,sizeof(head));
    cnt = 0;
}

但是在建图的时候，假设cap=10，flow=3，但这只是正向边。我们我们还需要录入反向边，也就是将cap设置为0，flow设置为-3这种网络叫做混合网络，将残余网络和实流网络混合在一起了：flow为正数的就是实流网络，负数为残余网络。
这样也能达到残余网络的效果，因为在增广路径上查找的时候是根据cap>flow走的，走反向边可以重新调整流量。

下面是在链式前向星中插入边的函数，这里一开始需要将flow设置为零流

1
2
3
4
5
6
7
void add(int u,int v,int c){
    E[cnt].v = v;
    E[cnt].cap = c;
    E[cnt].flow = 0;
    E[cnt].next = head[u];
    head[u] = cnt++;
}

下面是广搜的算法

首先每次广搜之前都需要对前驱数组和标志数组进行一个重置

然后是对链式前向星进行广搜。

在这里我们pop掉队列里的头节点后，我们遍历它的周围节点，符合条件的就将它加入到队列当中。条件是头结点到该结点的这条边的 cap必须大于flow，而且是未被访问过的结点。同时我们维护一个最小值d，始终记录着这条增广路的可增广量

如果v等于t，就说明找到了一条从s到t的增广路径，那么我们就可以进入下一步骤，即增流减流

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool bfs(int s, int t){
    memset(pre,-1,sizeof(pre));
    memset(vis,0,sizeof(vis));
    d = inf;
    queue<int>q;
    vis[s] = 1;
    q.push(s);
    while(!q.empty()){
        int u = q.front();
        q.pop();
        for(int i = head[u];~i/*i!=-1*/;i=E[i].next){
            int v = E[i].v;
            if(!vis[v]&&E[i].cap>E[i].flow){
                d = min(d,E[i].cap-E[i].flow);
                vis[v] = 1;
                pre[v] = i;//边的下标，而不是结点
                q.push(v);
                if(v==t)
                    return 1;
            }
        }
    }
    return 0;
}

接下来是EK方法，我们用while循环将所有的增广路径找出。然后通过第二个while循环对增广路径进行输出，并对实流网络增流和残余网络减流。这里有一个小技巧，对于链式前向星的对应边，只需要 $E[i\wedge1]$ 即可，因为我们录入的时候都是成对成对的。一直到输出s为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int EK(int s,int t){
    int maxflow=0;
    while(bfs(s,t)){//可以增广
        maxflow +=d;
        int v = t;
        cout<<"增广路径为："<<t;
        while (v!=s){
            int i = pre[v];
            E[i].flow +=d;
            E[i^1].flow -=d;
            v=E[i^1].v;
            cout<<"--"<<v;
        }
        cout<<"\t 增流："<<d<<endl;
    }
    cout<<endl<<"网络的最大流值: "<<maxflow<<endl;
    return maxflow;
}

输出网络函数，这里我们输出了链式前向星的结构

1
2
3
4
5
6
7
8
9
10
11
12
void printg(int n){
    cout<<endl;
    cout<<"----------网络(链式前向星):-------------"<<endl;
    for(int i = 1;i<=n;i++)
    {
        cout<<"v"<<i<<" ["<<head[i];
        for(int j = head[j];~j;j=E[j].next)
            cout<<"]--["<<E[j].v<<"\t"<<E[j].cap<<"\t"<<E[j].flow<<"\t"<<E[j].next;
        cout<<"]"<<endl;
    }
    cout<<endl;
}

还有一个输出实流边的函数。

1
2
3
4
5
6
7
8
9
10
void printflow(){//输出实流边
    cout<<endl;
    cout<<"----------实流边：----------"<<endl;
    for(int i=1;i<=n;i++)
        for(int j=head[i];~j;j=E[j].next)
            if(E[j].flow>0){
                cout<<"v"<<i<<"--"<<"v"<<E[j].v<<"\t"<<E[j].flow;
                cout<<endl;
            }
}

Dinic算法

-------------本文结束，感谢您的阅读-------------