哈夫曼编码

Posted on
Words count in article: 1.6k | Reading time ≈ 6

哈夫曼编码

通常的编码方法有固定长度和不等长度编码两种。

最优的编码方案的目的是使总码长度最短。利用字符的使用频率来编码使不等长编码方法，使得经常使用的字符编码较短，不常使用的字符编码较长。

不等长编码方法需要解决的两个关键问题：

1） 编码尽可能的短

使用频率高的字符编码较短，使用频率低的编码较长，可提高压缩率，节省空间，也能提高运算和通信速率。 即出现频率越高，编码越短

2) 编码不能有二义性

解决方法是：任何一个字符的编码不能是另一个字符编码的前缀，即前缀码特性

于是我们可以通过二叉树编码，频率高的可以离根近一点，频率低的就可以离根远一点。而且，每一个字符都是一个叶子结点，这样就可以避免二义性，因为叶子是绝对不会有孩子的。

我们可以构造一颗哈夫曼树，这是一棵将所要编码的字符作为叶子结点，该字符在文件中的使用频率作为叶子结点的权值，以自底向上的方式，通过n-1次的合并运算后构造的树。其核心思想是让权值大的叶子离根最近。

哈夫曼采取的贪心策略是：每次从树的集合中取出没有双亲且权值最小的两颗树作为左右子树，并一次构建一颗新的树。新书根节点的权值为其左右孩子节点权值之和，将新树插入到树的集合中

例子

为了方便起见，我们可以将频率同时扩大100倍。

  1. 我们选择没有双亲且权值最小的两个结点，$t_1,t_2$
  2. 将$t_1,t_2$作为左右子树构建一颗新的树,这里是a和d
  3. 将他们组合成一个新的树，他们的父结点的权重为12，这个12也需要加入到集合中作比较

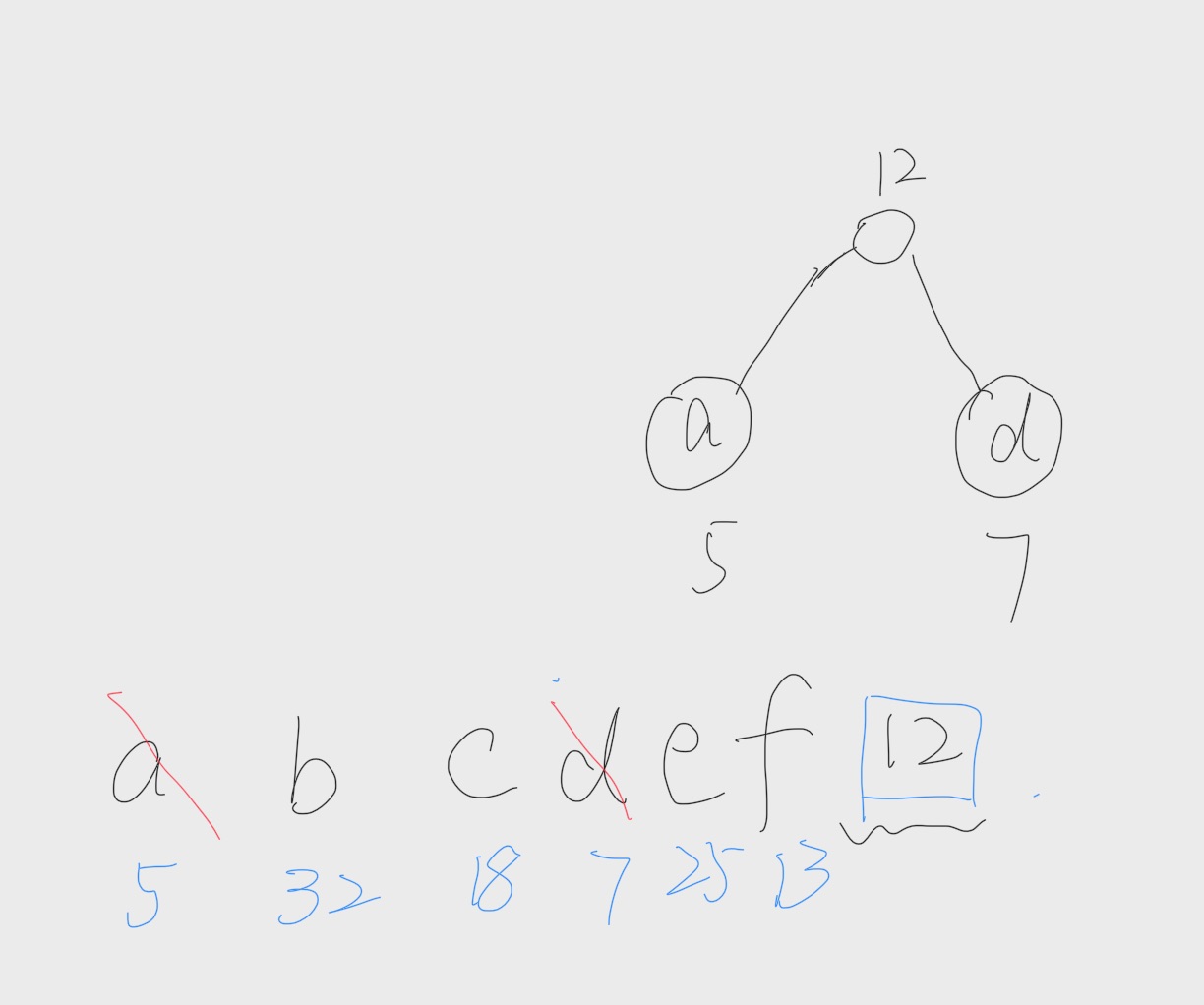
  1. 接下来，f 和新结点组合生成了新的树

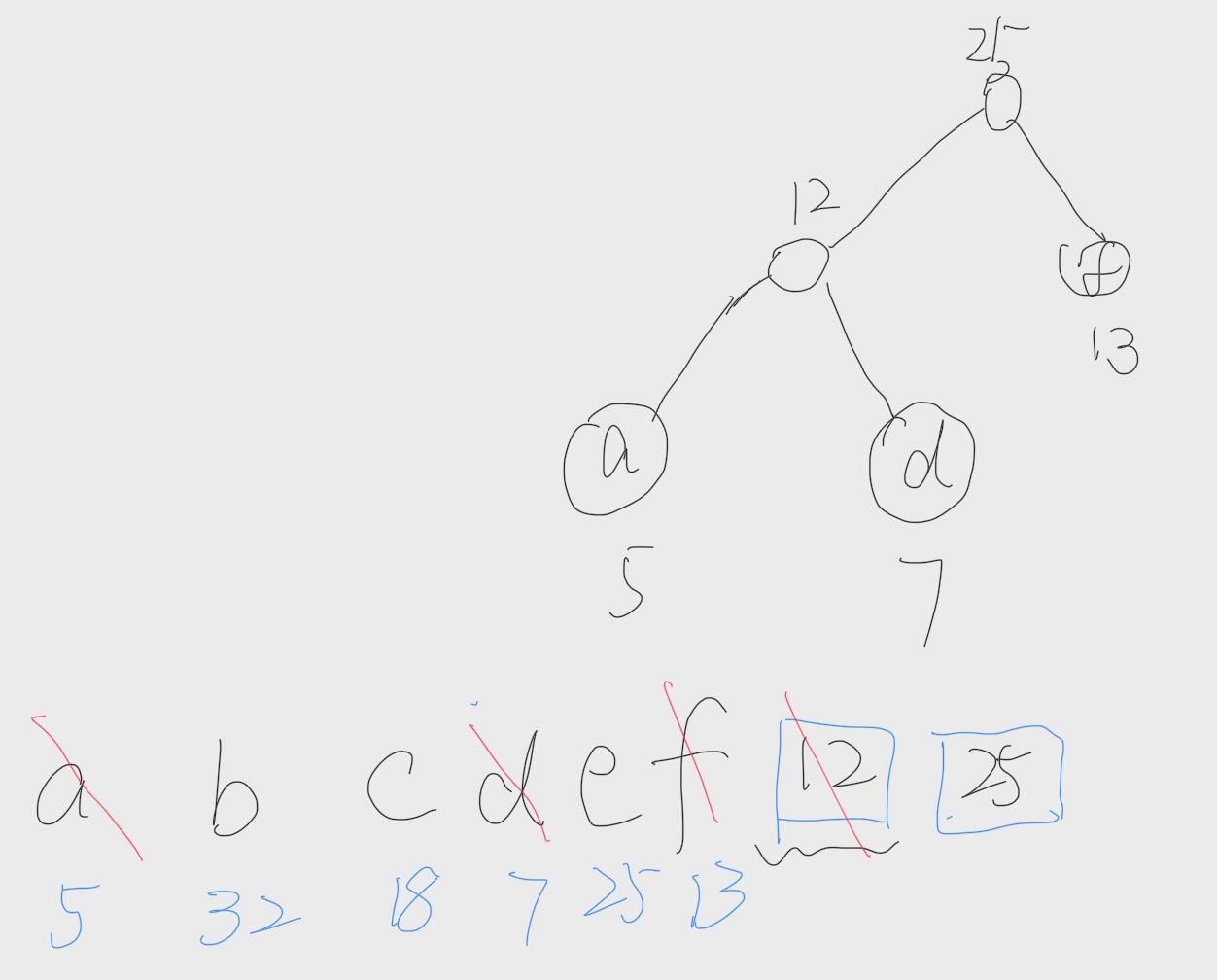
但是现在问题来了，当前的集合中，最小是c，次小为e和新的结点。我们该选哪个？ 答案是选择 e。因为新产生的结点会放在集合的后面。我们碰到一样权重的节点的时候，选择前面那个。

最后，我们的哈夫曼树如下：

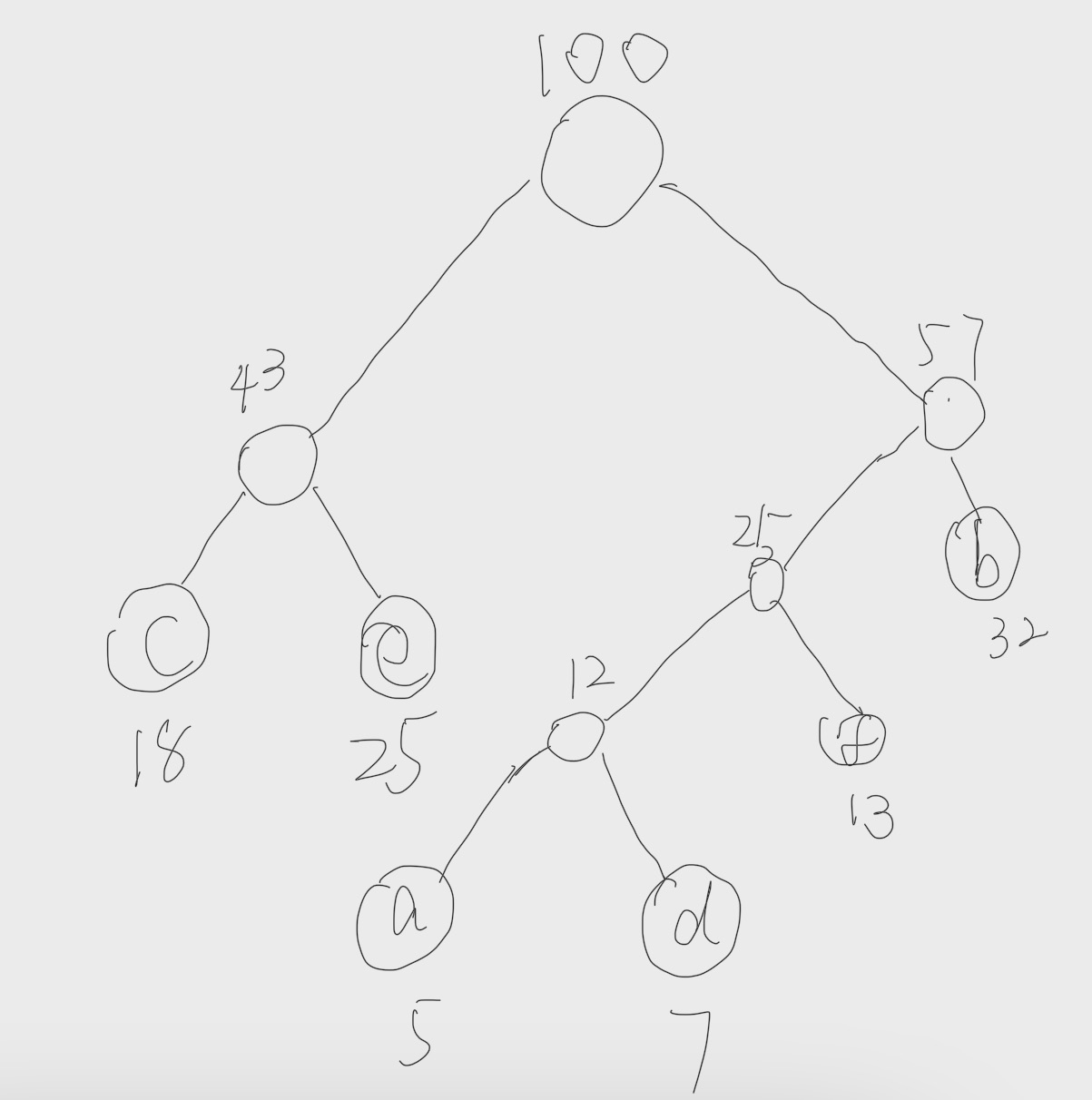
一般我们在程序中将最小的元素设置成左孩子，次小的设置成右孩子。

程序设计

确定合适的数据结构

  • 哈夫曼树中没有度为1的结点，则一颗n个叶子结点的哈夫曼树共有 2n-1 个结点(n-1次的合并，每次产生一个新的结点)
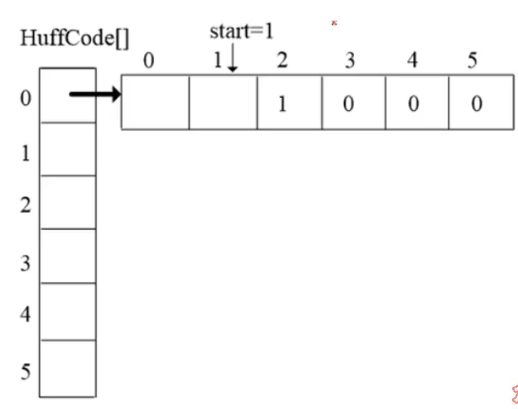
  • 构成哈夫曼树之后，为求编码需从叶子节点出发走一条从叶子到根的路径，是左孩子就编成0，是右孩子就编成1。
  • 译码需要从根出发走一条从根到叶子的路径，那么对于每个结点而言，我们要知道每个结点的权值、双亲、左孩子和右孩子和节点的信息
1
2
3
4
5
6
7
8
typedef struct
{
	double weight;
	int parent;
	int lchild;
	int rchild;
	char value;//该结点表示的字符
}HNodeType;

下面我们来写出哈夫曼树的构建数组

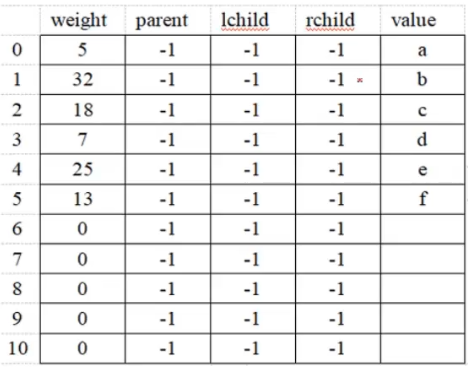
最终这张表如下图所示：

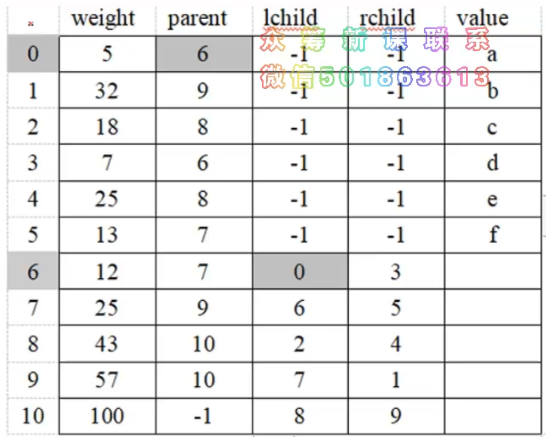
构建哈夫曼树的过程就是填写这张表的过程

编写哈夫曼编码的过程就是读表的过程

对于编码的存储，我们可以用这样一个struct数组：

1
2
3
4
5
typedef struct
{
	int bit[MAXBIT];//存储编码的数组，从后往前存
	int start;		//编码开始下标 
}HCodeType;

哈夫曼树带权路径长度

WPL = 每个叶子的权值X该叶子到根的路径长度之和。 哈夫曼树带权路径长度之和等于各新生成节点的权值之和 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include<bits/stdc++.h>
using namespace std;
#define MAXBIT    100
#define MAXVALUE  10000
#define MAXLEAF   30
#define MAXNODE   MAXLEAF*2 -1

typedef struct
{
    double weight;
    int parent;
    int lchild;
    int rchild;
    char value;
} HNodeType;

typedef struct
{
    int bit[MAXBIT];
    int start;
} HCodeType;
HNodeType HuffNode[MAXNODE];//定义一个结点结构体数组
HCodeType HuffCode[MAXLEAF];//定义一个编码结构体数组
void HuffmanTree (HNodeType HuffNode[MAXNODE],  int n){
    int i, j, x1, x2;//最小值的下标和次小值得下标
    double m1,m2;//最小值和次小值的权值
    for (i=0; i<2*n-1;i++)
    {
        HuffNode[i].weight=0;
        HuffNode[i].parent=-1;
        HuffNode[i].lchild=-1;
        HuffNode[i].rchild=-1;
    }
    for (i=0; i<n; i++)
    {
        cout<<"Please input value and weight of leaf node "<<i+1<<endl;
        cin>>HuffNode[i].value>>HuffNode[i].weight;//输入值和weight
    }
    for (i=0; i<n-1; i++)//n-1次合并
    {
        m1=m2=MAXVALUE;
        x1=x2=0;
        for (j=0;j<n+i;j++)//找最小，每次要加上新的结点
        {//满足的条件就是比m_1还小并且还没有父亲
            if (HuffNode[j].weight<m1&&HuffNode[j].parent==-1)
            {
                m2 = m1;
                x2 = x1;
                m1 = HuffNode[j].weight;
                x1 = j;
            }
            //或者比次小值还小，并且没有父亲结点
            else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)
            {
                m2=HuffNode[j].weight;
                x2=j;
            }
        }
        //更新节点的信息
        HuffNode[x1].parent  = n+i;
        HuffNode[x2].parent  = n+i;
        HuffNode[n+i].weight = m1+m2;
        HuffNode[n+i].lchild = x1;
        HuffNode[n+i].rchild = x2;
        cout<<"x1.weight and x2.weight in round "<<i+1<<"\t"<<HuffNode[x1].weight<<"\t"<<HuffNode[x2].weight<<endl; 
    }
}
void HuffmanCode(HCodeType HuffCode[MAXLEAF],  int n){
    HCodeType cd;//定义一个临时变量来存放求解编码时候的信息
    int i,j,c,p;
    for(i=0;i<n;i++)//从0号结点开始，为n个结点依次编码
    {
        cd.start=n-1; 
        c=i;
        p=HuffNode[c].parent;
        while(p!=-1)//从叶子向上找
        {
            if(HuffNode[p].lchild==c)
                cd.bit[cd.start]=0;
            else
                cd.bit[cd.start]=1;
            cd.start--;//start指向标前移一位
            c=p;//更新当前得结点以及它的父结点
            p=HuffNode[c].parent;
        }
        for (j=cd.start+1; j<n; j++)//将cd中的数组赋值给Huffcode
           HuffCode[i].bit[j]=cd.bit[j];
        HuffCode[i].start=cd.start;
    }
}
int main()
{
    int i,j,n;
    cout<<"Please input n:"<<endl;
    cin>>n;
    HuffmanTree(HuffNode,n);  
    HuffmanCode(HuffCode,n);
    for(i=0;i<n;i++)
    {
        cout<<HuffNode[i].value<<": Huffman code is: ";
        for(j=HuffCode[i].start+1;j<n;j++)
            cout<<HuffCode[i].bit[j];
        cout<<endl;
    }
    return 0;
}
-------------本文结束，感谢您的阅读-------------