算法期末复习
算法基础
插入排序
分治法
渐近符号
https://blog.csdn.net/so_geili/article/details/53353593
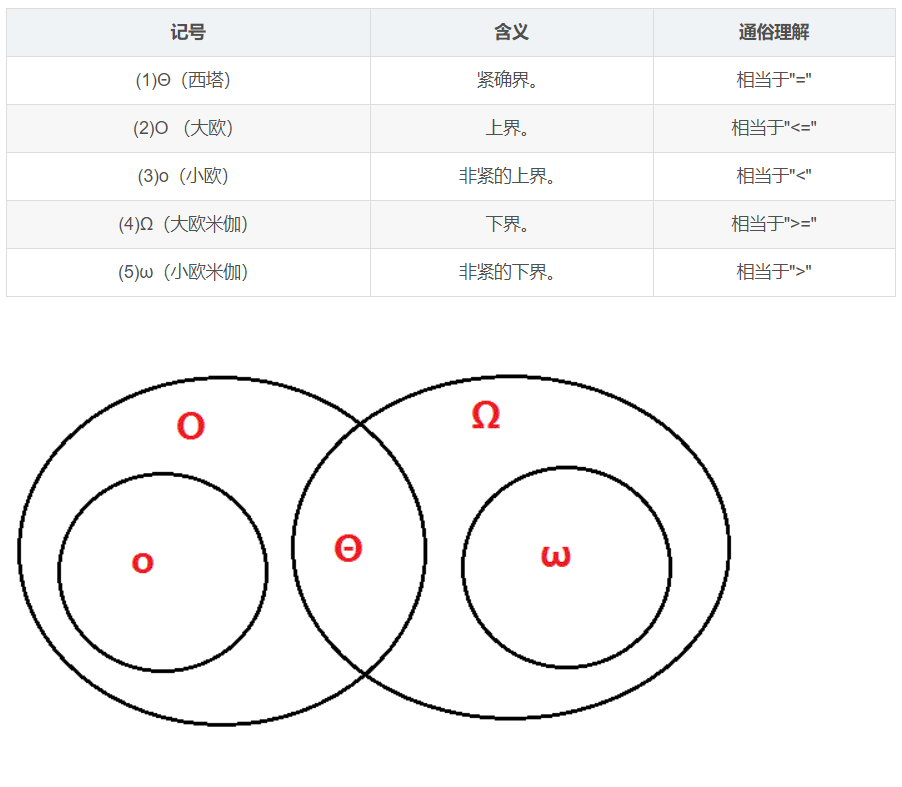
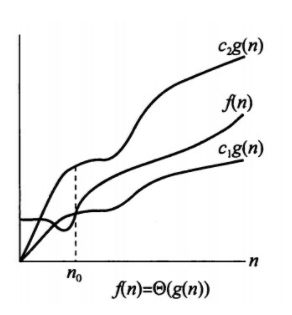
渐近紧确界记号 $\Theta$
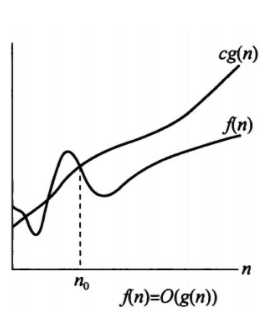
渐近上界记号:$O$
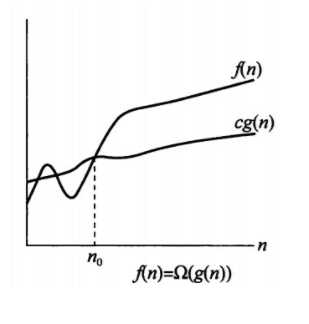
渐近下界记号:$\Omega$
非渐近紧确上界:$o$
小o和大O的区别就在于:
$O(n^2)$可以是 n,2n,1,$2n^2$等,但是$o(n^2)$ 可以是 n,1,3n等,但不能是 $n^2$ ,是 小于号的关系
非渐近紧确下界:$\omega$
和o与O的关系一样。$ω(n^2)$可以是$n^3,n^{10}$等,但不能是$n^2$。$Ω(n^2)$可以是$n^2,n^3$,$n^{10}$等。
分治策略*
矩阵乘法 Strassen
代入法求解递归式
递归树方法求解递归式
主方法求解递归式
堆排序
https://jasonxqh.github.io/2020/05/07/%E5%A0%86%E6%8E%92%E5%BA%8F/
快速排序
https://jasonxqh.github.io/2020/05/06/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F/
线性时间排序*
排序算法的下界
记数排序与基数排序
中位数和顺序统计量*
期望为线性的时间
最坏为线性的时间
散列表
散列表
https://jasonxqh.github.io/2020/05/09/hashtable/
开放寻址法
线性探查
给定一个普通的散列函数 h',称之为辅助散列函数,线性探查采用的散列函数为: $h(k,i)=(h’(k)+i)\mod~m$
二次探查
二次探查采用这种散列函数 $h(k,i)=(h’(k)+c_1i+c_2i^2)\mod m$
其中 $h’$ 是一个辅助散列函数,$c_1,c_2$为正的辅助常数
双重散列
双重散列是用于开放寻址法最好的方法之一,因为它所产生的排列具有随机选择排列的许多特性。双重散列采用如喜爱形式的散列函数
$h(k,i)=(h_1(k)+ih_2(k)) \mod m$
二叉搜索树
https://jasonxqh.github.io/2020/06/17/BSTandAVL/
概念
查询、插入、删除
红黑树
https://jasonxqh.github.io/2020/11/03/%E7%BA%A2%E9%BB%91%E6%A0%91/
性质、旋转、插入
动态规划
原理
钢条切割
矩阵链乘法
https://jasonxqh.github.io/2020/11/17/%E7%9F%A9%E9%98%B5%E9%93%BE%E4%B9%98%E6%B3%95/
贪心算法
原理
活动选择
1 |
|
赫夫曼编码
摊还分析*
聚合分析
核算法
势能法
动态表
图算法
图的表示
广度优先
https://jasonxqh.github.io/2020/08/30/BFSandDFS/
深度优先
https://jasonxqh.github.io/2020/08/30/BFSandDFS/
最小生成树
最小生成树的形成
Kruskal和Prim
https://jasonxqh.github.io/2020/06/21/%E5%9B%BE%E4%B8%8E%E8%B4%AA%E5%BF%83%E7%AE%97%E6%B3%95/
单源最短路径
Dijkstra算法
https://jasonxqh.github.io/2020/06/21/%E5%9B%BE%E4%B8%8E%E8%B4%AA%E5%BF%83%E7%AE%97%E6%B3%95/