Matlab 函数补充

我们没有必要了解ode23和ode45的内部原理，我们

比如我要求解一阶微分方程 $y’=cost$

f = @(t,y) cos(t); 	% 定义函数 f(t,y) = cos(t)
tspan = [0,2*pi];		% 时间范围
y0 = 2;					% 初值
[t,y] = ode23(f,tspan,y0); %注意调用格式

假如微分方程为 $F(y,y’,y’’,\cdots,y^{(n)},t) = 0$

初始条件 $y(t0)=c_0,y’(t_0)=c_1,\cdots,y^{n-1}(t_0) = c{n-1}$

首先做变量替换 : $x(1)=y,x(2)=y’,\cdots,x(n) = y^{(n-1)}$

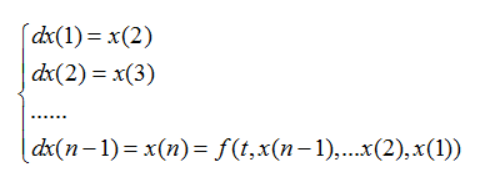
下面我们用转换好的微分方程组来编写 odefun函数

例题：首先写出常微分方程 $y’’ = -ty+e^ty’+3sin2t$ 的odefun函数

我们令$x(1)=y,x(2)=y’$那么，微分方程可以转换为 $dx(1)=y’=x(2),dx(2)=y’’ = -tx(1)+e^tx(2)+3*sin(2t)$

在matlab中我们可以这么写：

function dx=odefun(t,x);
dx = zeros(2,1);%初始化dx，生成一个2行1列的零向量存放我们的方程组
dx(1) = x(2);
dx(2) = -t*x(1)+exp(t)*x(2)+3*sin(2*t);

或者也可以直接写成向量形式

function dx=odefun(t,x);
dx = [
	x(2);
	-t*x(1)+exp(t)*x(2)+3*sin(2*t)
];

现在，我们要在$t = [3.9,4]$ 区间内求解微分方程 $y’’ = -ty+e^ty’+3sin2t,y{|t=3}=8,y’{|t=3}=2$

我们现在只要在原来的odefun基础上编写主函数，然后加上求解区间和边值条件即可，需要注意的是，ode45的运行结果以列向量的形式给出。因此在本例中，x的第一列为y，第二列为y’ . 如果遇到变量不是列向量的形式，可以考虑利用reshape函数进行矩阵变换

1
2
3

tspan = [3.9 4];
y0 = [8 2];
[t,x] = ode45('odefun',tspan,y0);

则，plot(t,x(:,1))画出来的是x的第一列数据，即为y；

plot(t,x(:,2))画出来的是x的第二列数据，即为y’；