datalab

Posted on
Words count in article: 3.3k | Reading time ≈ 15

datalab

这是我们做的第一个lab，题解是早就写在pdf里的，只是一直没有写成博客。现在我们来一题一题看：

int bitAnd(int x,int y)

首先是 bitAnd，顾名思义就是按位与：全是1结果才是1，有0结果就是0.

因为这题只能用 |和 ~ ，

比如说两个数都是1，那么取反后他们都是0，或一下再取反后就为1；两个数中间有一个1有一个0，那么去反之后还是有一个1一个0，或以下为1，再取反之后为0；同理如果两个数都为0，取反之后都为1，或一下再取反则为0.

因此这囊括了所有情况

1
2
3
4
int bitAnd(int x, int y)
{
  return ~(~x | ~y);
}

int getByte(int x,int n)

getByte这个函数要求我们再以十六进制计数的情况下以大端法取Byte，一个byte就是8bit，两位十六进制数。

首先我们先让n扩大8倍，因为一个n代表8个bit

然后我们让x右移n位，比如说n等于0就不移动，n=1时右移8位，n=2的时候右移16位，这样就能保证得到的数的倒数后8位(2进制形式)就是我们想要取得的byte

然后我们让其和 0xff 按位与。就能获得最后的答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * getByte - Extract byte n from word x
 *   Bytes numbered from 0 (LSB) to 3 (MSB)
 *   Examples: getByte(0x12345678,1) = 0x56
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 6
 *   Rating: 2
 */
int getByte(int x, int n)
{
  n = n << 3;
  x = x >> n;
  x = x & 0xff; // 取最后两位
  return x;
}

int logicalShift(int x, int n)

这是让我们实现逻辑右移，也就是向右移动k位，数字丢弃最高的k位，并在左端补上k个0.

但是我们知道，这不是unsigned而是int类型的，直接使用右移符号使用的是算术右移。因此我们要创造出一个mask，长这样 0x0...0f...f (n个0，32-n个1) 的掩码。

首先我们要获得 32-n这个数，因为直接用减号是非法的，我们可以用反码+1的方式取得n的负数然后再加上32. 在制作掩码的时候，如下图所示：

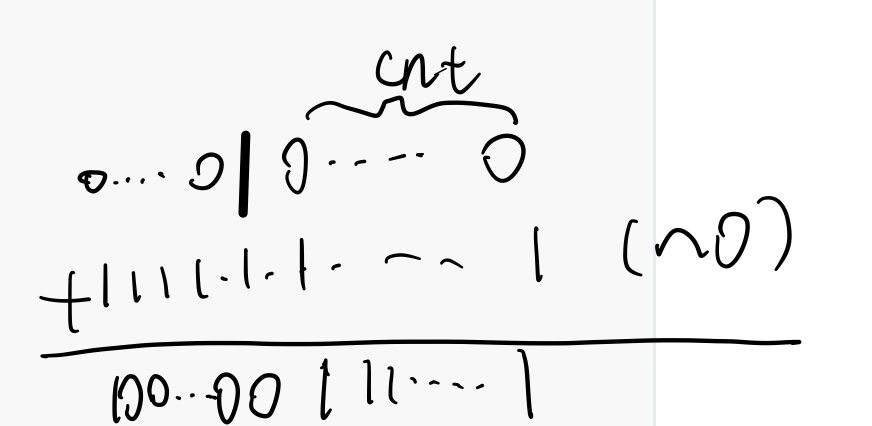
但是还有一种情况需要我们考虑，也就是当n=31, cnt=0 的时候，按理说我们应该得到的掩码是11….1(32个1),但是按照 (1<<cntn)+(~0) 的计算方法得到的却是 000…000(32个0),为了避免这种情况的发生，我们可以在后面再加一个 (((~(!n)) + 1)),这样当n=0的时候，这个式子的值就是 1....1; 而当n不等于0的时候，这个式子就等于 0....0，对最终结果是没有影响的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 
 * logicalShift - shift x to the right by n, using a logical shift
 *   Can assume that 0 <= n <= 31
 *   Examples: logicalShift(0x87654321,4) = 0x08765432
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 20
 *   Rating: 3 
 */
int logicalShift(int x, int n)
{
  int cntn = 32 + ((~n) + 1);
  int temp = (1 << cntn) + (~0) + (((~(!n)) + 1)); //1右移32位相当于1没移动
  return (x >> n) & temp;
}

int bitCount(int x)

这题的难度比较高，用语言比较难解释清楚。

首先我们要理解一个比特串中1的个数可以通过什么来计算？

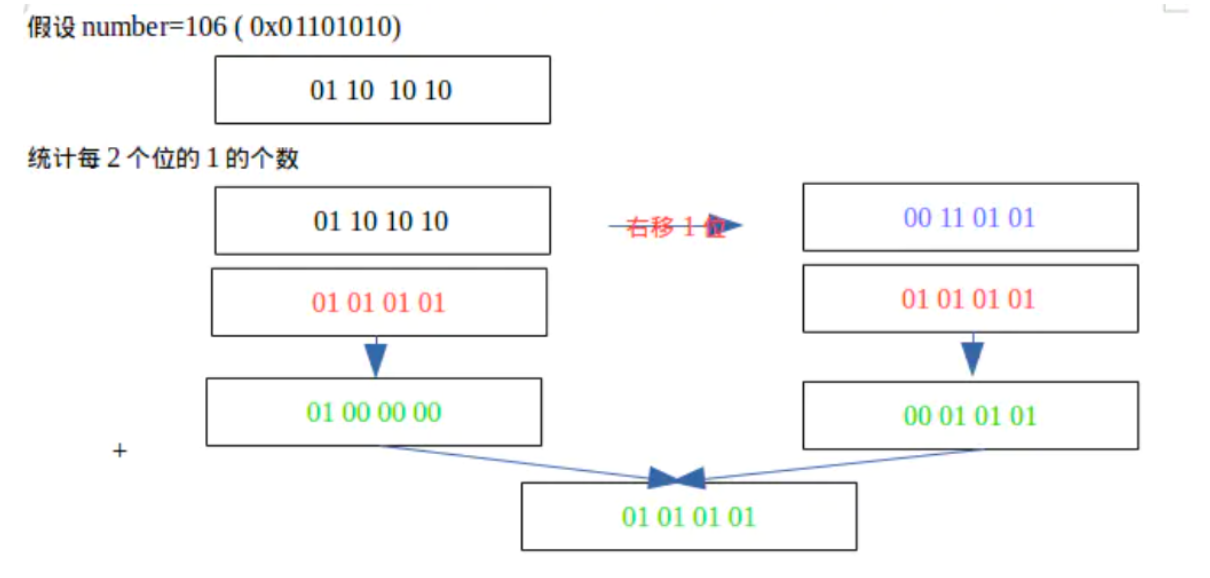
看懂了这张图就可以打开思路，一开始我们可以计算奇数位上的1个数和偶数位上的1的个数，得到一个新的比特串，再求两位中1的个数，4位中1的个数，最后求32位中1的个数。如下图所示：

那么我们怎么来根据这个原理来制作掩码呢？

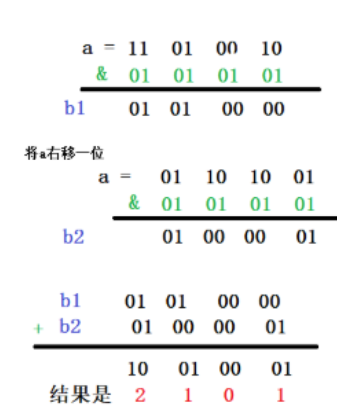
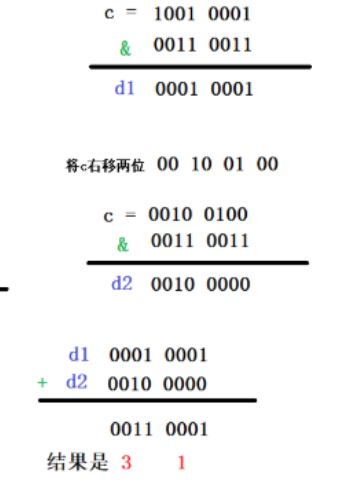
根据上面这样的计算步骤，扩展到32位，我们需要做5个掩码，分别是

010101....01, 00110011...0011,00001111000011110000111100001111，00000000111111110000000011111111, 11111111111111111111111111111111

因为我们不能直接使用十六进制来表现这些数，所以我们需要一些帮助比如： 0x55左移；0x33左移；0x0f左移，0xff左移

最后我们利用这些掩码和数字按位与并相加，最终得到比特串中1的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/*
 * bitCount - returns count of number of 1's in word
 *   Examples: bitCount(5) = 2, bitCount(7) = 3
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 40
 *   Rating: 4
 */
int bitCount(int x)
{
  int count;

  int tempmask = (0x55) | (0x55 << 8);
  int mask1 = (tempmask) | (tempmask << 16);

  int tempmask2 = (0x33) | (0x33 << 8);
  int mask2 = (tempmask2) | (tempmask2 << 16);

  int tempmask3 = (0x0f) | (0x0f << 8);
  int mask3 = (tempmask3) | (tempmask3 << 16);

  int mask4 = (0xff) | (0xff << 16);

  int mask5 = (0xff) | (0xff << 8);

  count = (x & mask1) + ((x >> 1) & mask1);
  count = (count & mask2) + ((count >> 2) & mask2);
  count = (count & mask3) + ((count >> 4) & mask3);
  count = (count & mask4) + ((count >> 8) & mask4);
  count = (count & mask5) + ((count >> 16) & mask5);
  return count;
}

int bang(int x)

这道题也比较简单，是计算非x的值，但是不能使用 ！

首先我们让x和其相反数取或来判断x是否等于0，当x不等于0的时候，temp等于1；当x等于0的时候，temp等于0

然后我们让temp算术右移31位，这时候若x不等于0，ans=11…11;若 x为0，ans=0

最后返回ans+1就是答案了

1
2
3
4
5
6
7
8
9
10
11
12
13
/* 
 * bang - Compute !x without using !
 *   Examples: bang(3) = 0, bang(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int bang(int x)
{
  int temp = x | ((~x) + 1);
  int ans = temp >> 31; //!0为11...11;0为 00..00
  return ans + 1;
}

int tmin(void)

这道题也非常简单，就是求补码的最小值，我们只要得到 100….00这个数就可以了。

1
2
3
4
5
6
7
8
9
10
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void)
{
  return 1 << 31;
}

int fitsBits(int x, int n)

这道题要我们判断x是否能被表示为n位数的补码形式

有两个规律: 假设n=4只有当[1xxx]或[0xxx] 我们才能用n个二进制位来表式x，然后我就将x往右移n-1位~((~n)+1)，判断剩下的数字是不是全1或者全0就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * fitsBits - return 1 if x can be represented as an 
 *  n-bit, two's complement integer.
 *   1 <= n <= 32
 *   Examples: fitsBits(5,3) = 0, fitsBits(-4,3) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 2
 */
int fitsBits(int x, int n)
{
  int temp = x >> (~((~n) + 1));
  int flag = (!temp | !(temp + 1));
  return flag; 
}

int divpwr2(int x, int n)

这道题要我们计算 $x/(2^n)$ 的值,只要我们了解二进制数除以$2^k$的 原理就能很好的解决。

这里我定义了 flag和 cnt，其中flag是判断这个二进制数是否为负数，若为负数，则为 1…1, 否则为0….0

cnt就是32-k个0和k个1，也就是$(1<<k)-1$ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * divpwr2 - Compute x/(2^n), for 0 <= n <= 30
 *  Round toward zero
 *   Examples: divpwr2(15,1) = 7, divpwr2(-33,4) = -2
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 2
 */
int divpwr2(int x, int n)
{
  int flag = x >> 31; //负数的话为 0xFFFFF否则为0
  //要构造 2^k-1; 也就是 32-k个0和k个1
  int cnt = ~((~0) << n);
  return (x + (flag & cnt)) >> n;
}

int negate(int x)

负数就是反码+1,这个题不用过多解释。

1
2
3
4
5
6
7
8
9
10
11
/* 
 * negate - return -x 
 *X   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x)
{
  return (~x) + 1;
}

int isPositive(int x)

这道题要我们判断x是否为正数，注意，0和负数都要返回0

首先我们判断这个数是负数还是非负数，若为负数，则返回1；否则返回0

然后我们还要判断这个数是不是等于0

最后将他们的按位或后的结果取反就是答案

1
2
3
4
5
6
7
8
9
10
11
12
13
/* 
 * isPositive - return 1 if x > 0, return 0 otherwise 
 *   Example: isPositive(-1) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 8
 *   Rating: 3
 */
int isPositive(int x)
{
  int flag = (x >> 31) & 0x1;
  int ifzero = !x;
  return !(flag^ifzero);
}

int isLessOrEqual(int x, int y)

这道题说 如果 $x<= y$ 就返回1，否则就返回0

这是有符号数，存在向上向下溢出的情况，我们必须考虑到所有情况。

第一种：x，y同号，且y-x 大于等于0

第二种：x,y 异号，只可能是 x小于0而y大于0

signx和signy是判断x，y是否小于0的，如果小于0，就为1；

samesignflag判断x和y是否同号，若同号则为1，若异号则为0；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y)
{
  int signx = (x >> 31) & 0x1;
  int signy = (y >> 31) & 0x1;
  int Samesignflag = !(signx ^ signy);
  int positiveflag = !(((~x) + 1 + y) >> 31);
  //要么同号相减大于0，要么异号 x小于0
  return (Samesignflag & positiveflag) | ((!Samesignflag) & signx);
}

int ilog2(int x)

想法是二分的思想，公式$log(x)=16a+8b+4c+2d+e$。那么count=abcde。因为x长32位，首先我们先将x>>16，判断高16位是不是还>0，如果>0，!(x>>16)就是0，我们要将他转换到a的位置就是将! !(x>>16)再次取非是1，然后<<4，到a的位置，就说明这个数大于16，1肯定在高16位处，然后在接着将高位折半到8位，就是>>8+16，看看高8位是不是也是>0。这样一步步下去就是答案了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*
 * ilog2 - return floor(log base 2 of x), where x > 0
 *   Example: ilog2(16) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 90
 *   Rating: 4
 */
int ilog2(int x)
{
  int count = 0;
  count = (!!(x >> 16)) << 4;
  count = count + ((!!(x >> (8 + count))) << 3);
  count = count + ((!!(x >> (4 + count))) << 2);
  count = count + ((!!(x >> (2 + count))) << 1);
  count = count + ((!!(x >> (1 + count))) << 0);

  return count;
}

unsigned float_neg(unsigned uf)

float-neg就是让我们求出浮点数的负数,我们知道浮点数 s,exp,frac 字段分别为 1 位， k=8 位和 n=23 位

给定一个浮点数,我们首先让temp=浮点数左移1位,这样开头8位就都是 exp字段了.

然后,我们必须去除掉NaN的情况,也就是 exp等于11111111,而后面的 frac字段不为零. 因此我们先让 wu&tmp是否等于wu,若相等,则位denormalized情况,然后再判断 temp!=wu 如果不等于,就是 NaN;如果等于,就是 Infinity的情况.如果是无穷的,那和普通的浮点数一样只要改变一下符号就可以了,如果是NaN就不用改, 直接返回NaN

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/* 
 * float_neg - Return bit-level equivalent of expression -f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representations of
 *   single-precision floating point values.
 *   When argument is NaN, return argument.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 10
 *   Rating: 2
 */
unsigned float_neg(unsigned uf)
{
  unsigned x = 0x80000000;
  unsigned wu = 0xFF000000;
  unsigned tmp = uf << 1;
  if ((wu & tmp) == wu) //FF后面不为0则为NaN
  {
    if (tmp != wu)
      return uf;
  }
  return uf ^ x;
}

unsigned float_i2f(int x)

这个函数要我们将一个有符号数x转换成浮点数的格式

浮点数的总共由3个部分组成,s,exp和frac

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/* 
 * float_i2f - Return bit-level equivalent of expression (float) x
 *   Result is returned as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point values.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned float_i2f(int x)
{
  unsigned ans;
  int tmpx = x;
  int f = 0;
  int delta = 0;
  int tail = 0;
  int E = 0;
//如果x等于0,那么就直接返回 x
  if (x == 0)
    return x;
  //如果x是最小值,即-2^31,那么 1 10011111 000..0 e=159,E=32,f=0,M=1
  if (x == 0x80000000)
    return 0xcf000000;

  ans = x & 0x80000000; //固定第一位,符号位

  if (ans)
    tmpx = -x; //若x是负数,那么tempx取x的相反数(为正)
//为了构造小数字段,我们先舍去1,然后再尾巴上补0,一直补到23位为止
  while ((tmpx >> E))//计算得到tmpx总共有几位
    E++;
  E = E - 1;
   //以12345为例,现在二进制表达为 11000000111001,E=13, 
  tmpx = tmpx << (31 - E);         //  然后tmpx左移18位,现在tmpx一共31位
    //tmpx = 11000000111001 000000000000000000
  tail = (tmpx >> 8) & 0x007FFFFF; //将tmpx右移8位,给阶码空出位置,现在tail为
    //10000001110010000000000
  f = tmpx & 0xff;
  //向偶数舍入
  delta = (f > 128) || ((f == 128) && (tail & 1));
  tail += delta;

  E = E + 127; // 计算阶码,E=e+偏移量
	
  //如果frac段大于23位了,那么就要在exp段加一个1,表示进一位,同时舍去最高位
  if (tail >> 23)
  {
    tail = tail & 0x007FFFFF;
    E += 1;
  }
  ans = ans | E << 23 | tail;//将这三段合并,得到最终的答案
  return ans;
}

unsigned float_twice(unsigned uf)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/* 
 * float_twice - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned float_twice(unsigned uf)
{
  //把浮点数拆成 s(1位)E(8位)M(23位),利用掩码分别取出
  int Smask = uf&0x80000000;
  int Emask = uf&0x7f800000;
  int Mmask = uf&0x007fffff;
  int E_infty = 0xff000000;
  int tempuf = uf<<1;
  int ans =uf;
    //首先要排除NaN的情况,如果uf是NaN,就返回uf
  if((tempuf&E_infty)==E_infty)
    return uf;
	//如果 exp这段不为0,那么就在exp这段加上1
  if(Emask!=0)
    ans = Smask+Mmask+Emask+0x00800000;
   //如果exp这段为0,说明是 denormalized,我们只需要将Mmask左移一位就可以了
  else if(Mmask!=0)
    ans = Smask+Emask+(Mmask<<1);
  return ans;
}
-------------本文结束，感谢您的阅读-------------