样本空间和概率
参考书本:
- 概率导论 第二版 Bertsekas 著
- 概率论与数理统计教程 第三版 峁时松 等著
集合
可数集与不可数集
集合按照可不可数可以分成两大类: 可数集与不可数集
如果 S 中的元素有限且可数,那么我们可以这样写: $S={x_1,x_2,\cdots,x_n}$
如果 S中的元素是无限的,但是它们是可以被枚举的(每个元素都能与然数集N的每个元素之间能建立一一对应的) ,我们可以将其写成:
$S={x_1,x_2,\cdots}$ 我们称其为 countably infinite (无限可数集). 比如说 ${0,2,-2,4,-4,\cdots}$
如果集合是这样被标示的: ${x|0\leq x \leq 1}$ ,那么 x 是连续的,不能被一一列举。因此我们称这样的集合为 uncountable (不可数集)
集合的操作
有一个集合S, 全集为 $\Omega$ , 那么称集合 S 的补集为 $S^c$
集合的交 : $S \cup T ={x|x\in S or x\in T}$
集合的并:$S\cap T = {x\in S and S\in T}$
集合的代数
德摩根律的一般形式需要牢记:

概率模型
基本构成
- 样本空间 $\Omega$ ,这是一个试验的所有可能结果的集合
- 概率律 , 概率律为试验结果的集合A(称之为事件) 确定一个非负数 $P(A)$
样本空间
每一个概率模型 都关联着一个 试验 ,这个试验将产生一个试验结果。 该实验的所有可能结果就形成了 样本空间。 需要注意:我们所讨论的概率模型的问题中,只设计一个试验,所以连续抛掷三次硬币只能作为一次试验,而不能认为是三次试验。其样本空间就是 {HHH,HHT,…, TTT}
样本空间可由若干个实验结果组成(如上面的硬币试验) ,也可以由无限多个试验结果组成。 例如:往一个方形目标上投掷飞镖,可将每个可能的弹着点作为试验的结果。
选择适当的样本空间在研究概率时十分重要。不同的实验结果必须是相互排斥的,这样在试验过程中只可能产生唯一的一个结果。 比如说:当试验是投掷一枚骰子的时候,不能把 “1 或者 3” 、“1或者4” 同时定义成一个结果,否则当骰子为1的时候,就不知道得到的是什么结果了
我们可以看两个游戏,并分别确定其样本空间:
游戏1 : 每次抛掷硬币的时候,子要出现正面向上,我们就可以赢得1元钱
游戏2: 在抛掷硬币的过程当中,直到出现第一次正面向上(含正面向上的那一次),以前的每次抛掷我们都可以赢1元钱(若10次抛掷都是正面向下,我们赢得10元)。若出现第一次正面向上以后还有机会抛掷硬币,则以后每次抛掷硬币的时候我们都可以赢2元钱,一直到第二次出现正面向上为止。 每次抛掷的到正面向上的时候,就翻倍。1,2,4…
那么在游戏1中,我们赢的钱数只与10次抛掷中正面向上的次数有关,因此,样本空间可由 11个(即0,1,2,…10) 试验结果组成,而在游戏2中,我们赢得的钱数不仅与正面出现的次数有关,也和正反面出现的顺序有关。因此,可能出现 $2^{10}$ 种可能,样本空间由所有长度为10的正反序列组成。
随机事件
随机现象的某些样本点组成的集合称为随机事件,简称事件。如在掷一颗骰子中, A=“出现奇数点” 是一个事件,即 $A={1,3,5}$ ,它是相应样本空间 $\Omega = {1,2,3,4,5,6}$
- 任一事件A是相应样本空间的一个子集。 在概率论中常常用韦恩图来表示
- 当子集中某个样本点出现了,就说事件A发生了。这是充分必要条件
- 事件可以用集合表示,也可以用明白无误的语言描述
- 由样本空间 $\Omega$ 中的单个元素组成的子集称为 基本事件 。 而样本空间 $\Omega$ 的最大子集(即$\Omega$本身) 称为必然事件。样本空间 $\Omega$ 的最小子集(即空集$\empty$) 称为不可能事件
随机变量
用来表示随机现象结果的变量称为随机变量 ,常用X,Y,Z 表示。很多事件都可以用随机变量表示,表示时应该写明随机变量的含义。
比如说投掷一颗骰子,可能出现1,2,3,4,5,6;若设置 $X=$ “掷一颗骰子出现的点数”, 则1,2,3,4,5,6就是随机变量X的可能取值。这时:
- 事件”出现3点”可用 “X=3” 表示
- “$X\leq$6” 是必然事件$\Omega$
现在我再设 $Y=$”掷一颗骰子6点出现的次数”,则 Y 是仅取0或者1 两个值的随机变量。这时
- “$Y=0$” 表示事件 “没有出现6点”
- “$Y\geq2$” 是不可能事件
因此,在同一个随机现象当中,不同的设置可以获得不同的随机变量。
事件间的关系
包含关系
如果属于A的样本点必属于B,则称A被包含在B中,或称B包含A. 记为 $A\subset B$ 事件A发生必然导致事件B发生
比如说掷一个骰子,事件 $A=$ “出现4点” 的发生必然导致事件 $B=$ “出现偶数点”的发生。
相等关系
如果属于A的样本点必属于B,且属于B的样本点必属于A,即 $A\subset B$ 且$B\subset A$ ,则称 事件A与B,记为 $A=B$
掷两颗骰子,以A记事件 ”两颗骰子的点数之和为奇数“,以B记事件”两颗骰子的点数为一奇一偶“
互不相容
如果A与B没有相同的样本点,则称A与B互不相容。A与B互不相容就是事件A与事件B不可能同时发生
事件间的运算
事件A与B的并
事件A与B的交
事件A与B的差
离散模型
离散概率律: 设样本空间由有限个可能的结果组成,则事件的概率可由组成这个事件的试验结果的概所决定,事件$P{s_1,s_2,\dots,s_n}=P(s_1)+P(s_2)+\cdots+P(s_n)$
现在假设样本空间 $\Omega={s_1,s_2,\cdots,s_n}$ ,并且每个实验结果都是等概率的。 利用归一化公理可知 $P(s_i) = 1/n,i = 1,2,\cdots , n$ ,我们得到:
离散均匀概率律(古典概型):设样本空间由n个等可能性的实验结果组成,因此每个实验结果组成的事件(被称为基本事件)的概率是相等的,由此得到:
$P(A)=\frac{含于事件A的试验结果数}n$
例子:考虑连续两次转动一个有 4 个边的骰子(放在桌子上转动)。 那么一共有16种可能的实验结果。这16种 每种出现的概率为 1/16 .
这是一个古典概型,在计算一个事件的概率的时候必须清楚这个事件所包含的试验结果数(基本事件数), 将这个结果除以16便得到这个事件的概率。
比如说: $P({两次点数总和为偶数}) = 8/16 = 1/2$
$P({第一次点数和第二次点数相同}) = 4/16 = 1/4$
$P({至少有一次转动的点数等于4}) = 7/16$
连续模型
A和B约定在某个时刻见面,而每个人到达约会地点的事件都会有延迟,延迟事件在0~1 小时。 第一个到达约会地点的人在哪儿等待15分钟,等了15分钟后若对方还没有到达约会地点,先到的人会离开约会地点。请问它们能够相会的概率有多大?
我们可以把这个问题抽象成一个单位正方形 $\Omega = [0,1]\times[0,1]$ 正方形中的每个点的两个坐标分别代表它们可能的延迟时间。 每个点都可以是他们的延迟时间且是等可能的。因此,我们可以将 $\Omega$ 的子集出现的概率定义为这个子集 的面积。 这个概率律满足概率的3条公里。 罗密欧和朱丽叶能够相会的时间可用这张图表示:
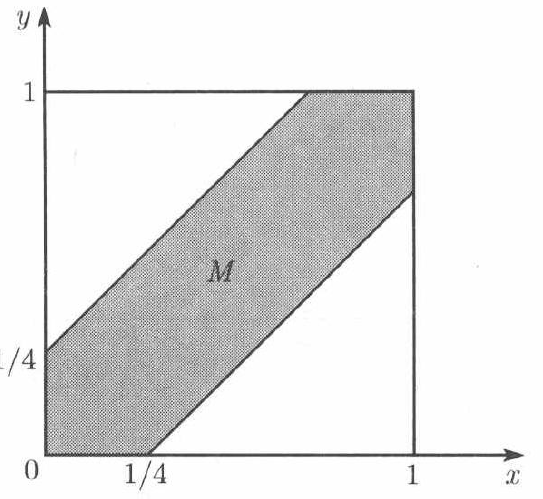
答案为: $\frac{7}{16}$
事件域
首先我们定义一下事件域:
设 $\Omega$ 为一样本空格键, $\mathcal F$ 为 $\Omega$ 的某些子集所组成的集合类。如果 $\mathcal F$ 满足:
- $\Omega \in\mathcal F$
- 若 $A\in \mathcal F$, 则 $\overline A\in \mathcal F$
- 若 $A1,A_2\cdots A_n\cdots \in \mathcal F$ , $\bigcup{i=1}^\infty A_i \in \mathcal F$
则称 $\mathcal F$ 为一个事件域,或者 $\sigma$ 域
例:
- 若样本空间只含两个样本点 $\Omega={\omega_1,\omega_2}$ ,记 $A={\omega_1},\overline A = {w_2}$ ,其事件域为 $\mathcal F = {\emptyset,A,\overline A,\Omega}$
- 若样本空间含有n个样本点$\Omega={\omega_1,\omega_2\cdots,\omega_n}$ 其事件域 $\mathcal F$ 是由空集 $\emptyset$ 、n个单元素集, $\begin{pmatrix} n \ 2 \end{pmatrix}$ 个双元素集、$\begin{pmatrix} n \ 3 \end{pmatrix}$ 个三元素集……和$\Omega$组成的集合类,这时 $\mathcal F$ 中共有 $\begin{pmatrix} n \ 0 \end{pmatrix}+\begin{pmatrix} n \ 1 \end{pmatrix}+\cdots+\begin{pmatrix} n \ n \end{pmatrix}=2^n$ 个事件。
概率的定义及其性质
概率的定义:
设 $\Omega$ 是一个样本空间,$\mathcal F$ 为 $\Omega$ 的某些子集组成的一个事件域。如果对任意事件 $A\in\mathcal F$ 定义在 $\mathcal F$ 上的一个实质函数 $P(A)$ 满足:
1) 非负性公理: 若 $A\in \mathcal F$ ,则 $P(A)\geq 0$ ;
2) 正则性公理:$P(\Omega)=1$
3) 可列可加性公理: 若 $A1,A_2,\cdots, A_n,\cdots$互不相容,则: $P(\bigcup{i=1}^\infty Ai) = \sum{i=1}^{\infty} P(A_i)$
则称 P(A) 为事件 A的概率, 称三元素 $(\Omega ,\mathcal F,P)$ 为概率空间。
概率的性质:
概率的可加性
有限可加性
若有限个事件 $A1,A_2,\cdots,A_n$ 互不相容,则有 $P(\bigcup{i=1}^n Ai) = \sum{i=1}^{n}P(A_1)$ 注意了,可列可加性和有限可加性是不同的。
由于有限可加性,我们就可以得到以下求对立事件概率的公式:对任一事件 A, $P(\overline A) =1-P(A)$
概率的单调性
性质1
若 $A\supset B$ ,则 $P(A-B)=P(A)-P(B)$
进而可以推出: 若$A\supset B$, 则 $P(A)\geq P(B)$
性质2
对任意两个事件 A,B, 有 $P(A-B)=P(A)-P(AB)$
概率的加法公式
性质1
对任意的两个事件A,B 有 $P(A\cup B)=P(A)+P(B)-P(AB)$
对任意n个事件 $A1,A_2,\cdots,A_n$ ,有 $P(\bigcup{i=1}^n Ai)= \sum{i=1}^n P(Ai)-\sum{1\leq i<j\leq n} P(AiA_j)+\sum{1\leq i<j<k\leq n}P(A_iA_jA_k)+\cdots+(-1)^{n-1}P(A_1A_2\cdots A_n)$
据此,可以推出 半可加性, 对任意两个事件 A,B 有
$P(A\cup B)\leq P(A)+P(B)$
对任意n个事件 $A1\cdots A_n$ ,有 $P(\cup{i=1}^n)\leq \sum_{i=1}^n P(A_i)$
概率的连续性
首先我们给出两个定义: 极限事件和上下连续
极限事件
- 对 $\mathcal F$ 中任一单调不减的事件序列 $F1\subset F_2\subset \cdots \subset F_n\subset \cdots$ ,称可列并 $\bigcup{n=1}^\infty Fn$ 为 ${F_n}$ 的极限事件,记为 $\lim\limits{n\rightarrow \infty} Fn= \bigcup{n=1}^\infty F_n$
- 对 $\mathcal F$ 中任一单调不增 的事件序列 $E1\supset E_2\supset \cdots\supset E_n\supset \cdots$ ,称可列交 $\bigcap{n=1}^\infty En$ 为 ${E_n}$ 的极限事件,记为 $\lim\limits{n\rightarrow \infty} En=\bigcap{n=1}^\infty E_n$
上下连续
对 $\mathcal F$ 上的一个概率 P
- 若它对$\mathcal F$ 中任一单调不减的时间序列 ${Fn}$ 均成立 $\lim\limits{n\rightarrow \infty}P(Fn)=P(\lim\limits{n\rightarrow \infty } F_n)$ 则称概率P是下连续的
- 若它对$\mathcal F$ 中任一单调不增的时间序列 ${En}$ 均成立 $\lim\limits{n\rightarrow \infty}P(En)=P(\lim\limits{n\rightarrow \infty } E_n)$ 则称概率P是上连续的
概率的连续性定义:
若 P 为 事件域 $\mathcal F$ 上的概率,则 P 既是下连续的,又是上连续的。(证明见书本 Prob&Stat P34)
条件概率
条件概率的定义
设 A与B 是严格不能空间 $\Omega$ 中的两事件,若 $P(B)>0$, 则称 $P(A|B)=\frac{P(AB)}{P(B)}$ 为 “在B发生下A的条件概率“,简称条件概率
要注意,条件概率也是概率,也满足概率的三个定义:
- 非负性: $A\in \mathcal F$ ,则 $P(A|B)\geq 0$ ;
- 归一性: $P(\Omega|B)=1$
- 可列可加性:$A1,A_2,\cdots,A_n,\cdots$互不相容, 则 $P(\bigcup{n=1}^\infty An|B)=\sum{n=1}^\infty P(A_n|B)$
乘法公式
公式
- 如果 $P(B)>0$ 则 $P(AB)=P(B)P(A|B)$
- 进而可推出 若 $P(A1A_2\cdots A{n-1})>0$ ,则 $P(A1A_2\cdots A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\cdots P(A_n|A_1A_2\cdots A{n-1})$
罐子模型
全概率公式
公式:设 $B1,B_2,\cdots ,B_n$ 为样本空间$\Omega$ 的一个分割,,如果 $P(B_i)>0,i=1,2,\cdots ,n$ 则对事件 A有 : $P(A)=\sum{i=1}^n P(B_i)P(A|B_i)$
对于全概率公式,我们要注意:
- 全概率公式的最简单形式 假如 $0<P(B)<1$ 则 $P(A)=P(B)P(A|B)+P(\overline B)P(A|\overline B)$
- 将条件从分割改为 $B_1,B_2,\cdots,B_n$ 互不相容, 全概率公式仍然成立
- 对可列个事件 $B1,B_2,\cdots,B_n\cdots $互不相容,且 $A\subset \bigcup{i=1}^n B_i$ 则全概率公式仍成立,只要将右边改成可列向项之和即可。
贝叶斯公式
贝叶斯公式是在乘法公式和全概率公式的基础上推导而来
公式: 设 $B_1,B_2\cdots ,B_n$是样本空间 $\Omega$ 的一个分割,如果 $P(A)>0,P(B_i)>0, ~i =1,2,\cdots,n$ 则:
$P(Bi|A)=\frac{P(B_i)P(A|B_i)}{\sum{j=1}^n P(B_j)P(A|B_j)}$
独立性
两个事件的独立性
若 $P(AB)=P(A)P(B)$ 成立,最称事件 A与 B相互独立,简称 A与B 独立。否则称A与B不独立或相依
性质
若事件 $A$与$B$ 独立,则$ A$与 $\overline B$ 独立 ,$\overline A$与 $B$ 独立, $\overline A$与 $\overline B$ 独立。注意:相互独立事件又不是互斥事件,本来就可以同时发生的
两个事件不可能既互斥又相互独立。
相互独立的事件之间没有影响,事件A的发生当然不会影响事件B的发生,两个事情是否同时发生都是有可能的。
互斥的事件当然不是独立的,因为一件事情的发生已经影响到了另外一件事的发生了。
多个事件的相互独立性
两两独立
设 A,B,C 是三个事件, 如果有:
$\begin{cases}P\left( AB\right) =P\left( A\right) P\left( B\right) \ P\left( AC\right) =P(A)P\left( C\right) \ P\left( BC\right) =P(B)P\left( C\right) \end{cases}$
则称 $A,B,C$ 两两独立。
相互独立
若还有: $P(ABC)=P(A)P(B)P(C)$ 则称 A,B,C 相互独立。
要注意,两两独立不一定推出相互独立,相互独立也不一定能推出两两独立。
化简到一般形式:$\begin{cases}P\left( A{i}Aj\right) =P\left( A{i}\right) P\left( Ai\right) \ P\left( A{i}A{j}A{k}\right) =P\left( A{i}\right) P(Aj)P\left( A_n\right) \ \ldots \ldots \ P\left( A_1A{2}\ldots A{n}\right) =P(A_1)\cdot P\left( A{2}\right) \ldots P(A_{n}) \end{cases}$
则称此 n个事件 $A_1,A_2,\cdots, A_n$ 相互独立。
实战注意点:
- 互不相容 可以简化事件并的概率计算,相互独立 可以简化事件交的概率计算。 主要表现为:若事件 A、B、C互不相容,那么$P(A\cup B\cup C)=P(A)+P(B)+P(C)$ ; 若事件A、B、C 相互独立,那么
P(ABC)=P(A)P(B)P(C) - 运用对偶法,可以把事件并转化成事件交。
对偶律: $(A\cup B)^c = A^c\cap B^c$ , $(A\cap B)^c = A^c\cup B^c$
右上角C表示此集合的补集
语言描述:
①A并B的补集 = A的补集交B的补集
②A交B的补集 = A的补集并B的补集
例题: 三个人独立地破译一个密码,它们能单独破译密码的概率分别是 $1/5,1/3,1/4$ 求密码被破译的概率
$P(B)=P(A_1\cup A_2\cup A_3)= P(A_1^c)\cap$