随机变量及其分布
定义在样本空间$\Omega$上的实值函数 $X=X(\omega)$ 称为随机变量,通常用大写的字母 X,Y,Z等表示随机变量,其取值用小写字母 x,y,z 等表示。
假如一个随机变量尽可能取有现个或可列个值,则称其为离散随机变量;假如一个随机变量的可能取之充满数轴上的一个区间 $(a,b)$ ,则称其为连续随机变量,其中a或b可以是 $\infty$
随机变量的分布函数(CDF)
设 X 是一个随机变量,对任意实数x,称 $F(x) =P(X\leq x)$ 为随机变量X的分布函数。 且称 $X$ 服从 $F(x)$ , 记为$X\sim F(x)$ 。
三条基本性质:
- 单调性 $F(x)$ 是定义在整个实数轴上的单调非减函数 ,即对任意的 $x_1<x_2$ ,有 $F(x_1)\leq F(x_2)$
- 有界性 对任意的x,都有 $0\leq F(x)\leq 1$ 且 $F(-\infty) = \lim\limits{x\rightarrow-\infty}F(x) = 0$; $F(\infty) = \lim\limits{x\rightarrow\infty}F(x)=1$
- 右连续性 $F(x)$ 是 x 的右连续函数,即对任意的 $x0$ ,有 $\lim\limits{x\rightarrow x_0^{+0}}F(x)=F(x_0)$ ,即 $F(x_0+0)=F(x_0)$
右连续性在计算分布函数中的未知参数有很大的作用。
这三条基本性质也成为了判别某个函数是否能成为分布函数的充要条件
接下来还会说CDF是概率密度函数(PDF)的积分
有了随机变量 X的分布函数,那么有关 X 的各种事件的概率都能方便的用分布函数来表示了。例如对任意的实数 a、b,有:
- $P(a<X\leq b) = F(b)-F(a)$
- $P(a<X<b)=F(b-0)-F(a)$
- $P(a\leq X\leq b)=F(b)-F(a-0)$
- $P(a\leq X<b)=F(b-0)-F(a-0)$
- $P(X=a)=F(a)-F(a-0)$
- $P(X\geq b)=1-F(b-0)$
- $P(X>b)= 1-F(b)$
- $P(X<b)=F(b-0)$
特别当 F(x) 在 a与b 处连续时,有 $F(a-0)=F(a), F(b-0)=F(b)$
上面这几个 公式非常重要,我们要牢牢基础。
离散随机变量的概率分布列
设 X 是一个离散随机变量,如果 X 的所有可能取值是 $x_1,x_2,\cdots,x_n,\cdots$ ,则称 X 取 $x_i$ 的概率。则称 X 取 $x_i$ 的概率 $p_i = p(x_i)=P(X=x_i),i=1,2,\cdots,n,\cdots$ 为 X 的概率分布列或简称分布列,记为 $X\sim {p_i}$
分布列的基本性质
- 非负性 $p(x_i)\geq 0,i=1,2\cdots$
- 正则性 $\sum_{i=1}^\infty p(x_i)=1$
由离散随机变量 X 的分布列很容易写出 X的分布函数
连续随机变量的概率密度函数(PDF)
设随机变量X 的分布函数为 $F(x)$ ,如果存在实数轴上的一个非负可积函数$p(x)$,使得对任意函数x有 $F(x) = \int_{-\infty}^x p(t)dt$ ,则称 $p(x)$ 为 X 的概率密度函数,简称密度函数 ,同时称 X 为连续随机变量,称 $F(x)$ 为连续分布函数
简单的来说就是PDF是CDF的一阶导数。
密度函数的基本性质
- 非负性 $p(x)\geq 0$
- 正则性 $\int_{-\infty}^{\infty} p(x)dx = 1$
譬如已知某个函数 $p(x)$ 为密度函数,若$p(x)$ 中有一个待定常数,那么我们就可以利用正则性 $\int_{-\infty}^{\infty} p(x)dx = 1$ 来确定该常数的值。
均匀分布
当分布函数(CDF)为:$F\left( x\right) =\begin{cases}0,x <a\ \dfrac{x-a}{b-a},a\leq x\leq b\ 1,~~x >b\end{cases}$, 密度函数(PDF)为$\begin{cases}\dfrac{1}{b-a},a <x <b\ 0, {其他}\end{cases}$时,这个分布就是区间 $(0,a)$上的均匀分布,记为 $U(a,b)$
随机变量的数学期望
设离散随机变量 X 的分部列为 $p(x_i) = P(X=x_i),i = 1,2,…,n…$
如果 $\sum{i=1}^\infty |x_i|p(x_i)<\infty$ ,则称 $E(X) = \sum{i=1}^\infty x_ip(x_i)$ 为随机变量的期望或均值。注意,期望一定要收敛,否则期望便不复存在。
同样的,对于连续随机变量 X 的密度函数为 $p(x)$ ,如果 $\int{-\infty}^{\infty}|x|p(x)dx<\infty$ ,则称 $E(X) = \int{-\infty}^{\infty} xp(x)dx$ 为X的数学期望。
期望的一些性质
定理: 若随机变量 X 的分布用分布列 $p(xi)$ 或用密度函数 $p(x)$ 表示,则 X 的某一函数$g(X)$ 的数学期望为 $E[g(X)]=\begin{cases}\sum{i}g(xi)p(x_i) ,在离散场合 \ \int{-\infty}^{\infty}g(x)p(x)dx, {在连续场合}\end{cases} $
- 性质1:设c是常数,则 $E(c) = c$
- 性质2:对任意常数 a 有 $E(aX)=aE(X)$
- 性质3:对任意的两个函数 $g_1(x)$和 $g_2(x)$ 有: $E[g_1(x)\pm g_2(x)] = E[g_1(x)]\pm E[g_2(x)]$
例题
设连续随机变量 X 的分布函数为 $F(x)$ ,且数学期望存在,证明:
$E(X) = \int0^{+\infty} [1-F(x)]dx-\int{-\infty}^0F(x)dx$
解:
将第一个积分改写为二次积分,然后改变积分次序,得到:
第二个积分也可以写成二次积分并改变积分次序:
因此当X 为非负的连续随机变量,且 $E(X^n)$ 存在,则可证明:
- $E(X) = \int{0}^{+\infty} [1-F(x)]dx =\int{0}^\infty P(X>x)dx$
- $E(X^n) =\int_0^\infty n x^{n-1} P(X>x)dx$ 证明: $E(X^n)=\int_0^\infty P(X^n>y)dy$ , 那么当 $y=x^n$ 的时候,实际上我们可以得到 $E(X^n)=\int_0^\infty P(X^n>x^n)nx^{n-1}dx$ , 即$E(X^n)=\int_0^\infty P(X>x)nx^{n-1}dx$
随机变量的方差与标准差
若随机变量 $X^2$ 的数学期望 $E(X^2)$ 存在,则称偏差平方 $(X-E(X))^2$ 的数学期望 $E(X-E(X))^2$ 为随机变量$X$ 为随机变量 $X$ 的方差,记为 $Var(X) = E(X-E(X))^2 = \begin{cases}\sumi(x_i-E(X))^2p(x_i),在离散场合\ \int{-\infty}^\infty (x-E(X))^2p(x)dx, {在连续场合}\end{cases}$
并称方差的正平方根 $\sqrt{Var(X)}$为随机变量(或相应分布) 的标准差,记为 $\sigma(X)$或$\sigma_X$
当随机变量X的数学期望存在时,方差不一定存在;而当X的方差存在时,则E(X)必定存在
方差的性质
性质1:
$Var(X) = E(X^2)-[E(X)]^2$
在实际计算方差的时候,这个性质往往比定义 $Var(X) = E(X-E(X))^2$ 更加常用
证明:$Var(X) = E(X^2)-2E(X)*E(X)+(E(X))^2 = E(X^2)-(E(X))^2$
性质2:
常数的方差为0,即 $Var(c) = 0$
若c是常数,则 $Var(c) = E(c-E(c))^2 = E(c-c)^2 = 0$
性质3:
若a,b是常数,则 $Var(aX+b) = a^2Var(X)$
切比雪夫不等式
设随机变量X 的数学期望和方差都存在则对任意常数$\epsilon>0$ ,有 $P(|X-E(X)|\geq \epsilon)\leq \frac{Var(X)}{\epsilon^2}$
通过二次放缩的方法可以证明:记 $E(X)=a$
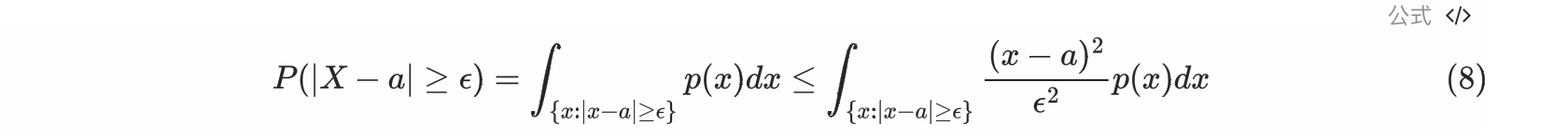
因为 $|x-a|\geq \epsilon$, 所以 $\frac{|x-a|^2}{\epsilon^2}\geq 1$
然后进行第二次缩放,将原来的积分范围修改成整个实数域
积分部分的值就是方差的定义,因此积分等于$Var(X)$
在概率论中,时间 $||X-E(X)|\geq \epsilon|$称为大偏差,其概率 $P(|X-E(X)|)\geq \epsilon$称为大偏差发生概率。切比雪夫不等书给出大偏差发生概率的上界,这个上界与方差成正比,方差越大、上界也就越大。