常用离散分布

二项分布

二项分布： X = “n次伯努利试验中成功的次数”

取值范围：0~n，为整数

分布列：$P(X=k)C_n^k p^k(1-p)^{n-k},k=0,1,\cdots,n$

记为： $X \sim b(n,p)$

二点分布

当 n=1 时的二项分布 $b(1,p)$ 称为二点分布，或称 0-1分布，或称伯努利分布。

取值范围： 0，1

分布列： $P(X=x) = p^x(1-p)^{1-x}$

二点分布主要用来描述一次伯努利试验中成功地次数(0或1)

泊松分布

分布列： $P(X=k)=\frac{\lambda^k}{k!} e^{-\lambda},k=0,1,2,\cdots$ 其中，参数 $\lambda>0$ ，记为 $X\sim P(\lambda)$

通过级数的知识，我们很容易验证泊松分布的正则性： $\sum{k=0}^\infty \frac{\lambda^k}{k!}e^{-\lambda}=e^{-\lambda}\sum{k=0}^{\infty} \frac{\lambda^k}{k!} =e^{-\lambda}e^{\lambda} = 1$

泊松分布常常用来刻画单位时间、单位面积上发生的次数。

泊松分布和二项分布的关系：在n重的伯努利试验中，设成功的概率为 $pn$ 当 $n\rightarrow \infty$ ，且 $n*p_n \rightarrow n$ 时，我们有 $\lim\limits{n\rightarrow \infty}C_k^n p_n^k (1-p_n)^{n-k} = \frac{\lambda^k}{k!} e^{-\lambda}$

泊松分布的概率质量函数(pmf) ：

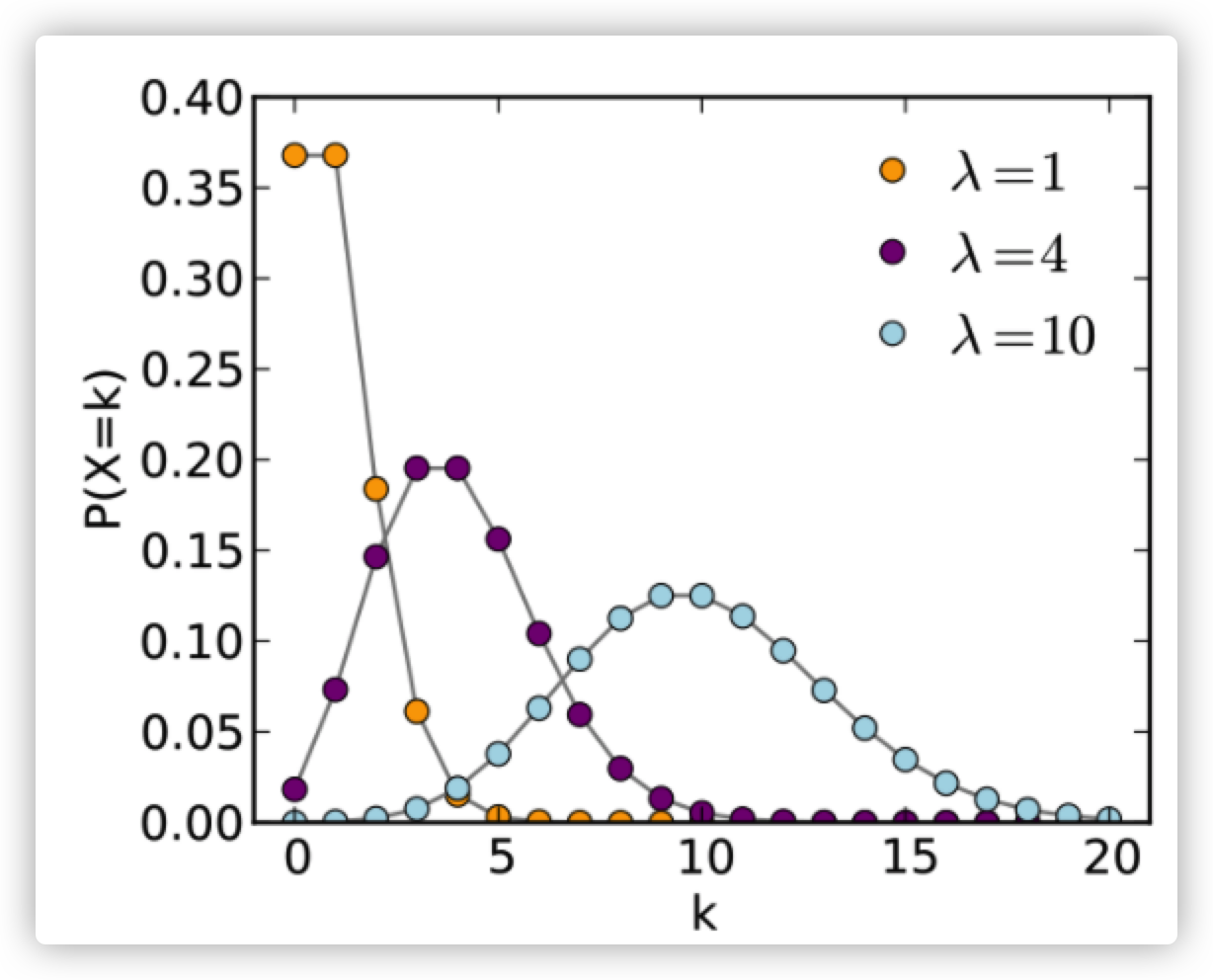
对泊松分布的pmf做出的解释：每个点的意义就是单位时间或者面积内随机事件发生k次的概率。

CDF:

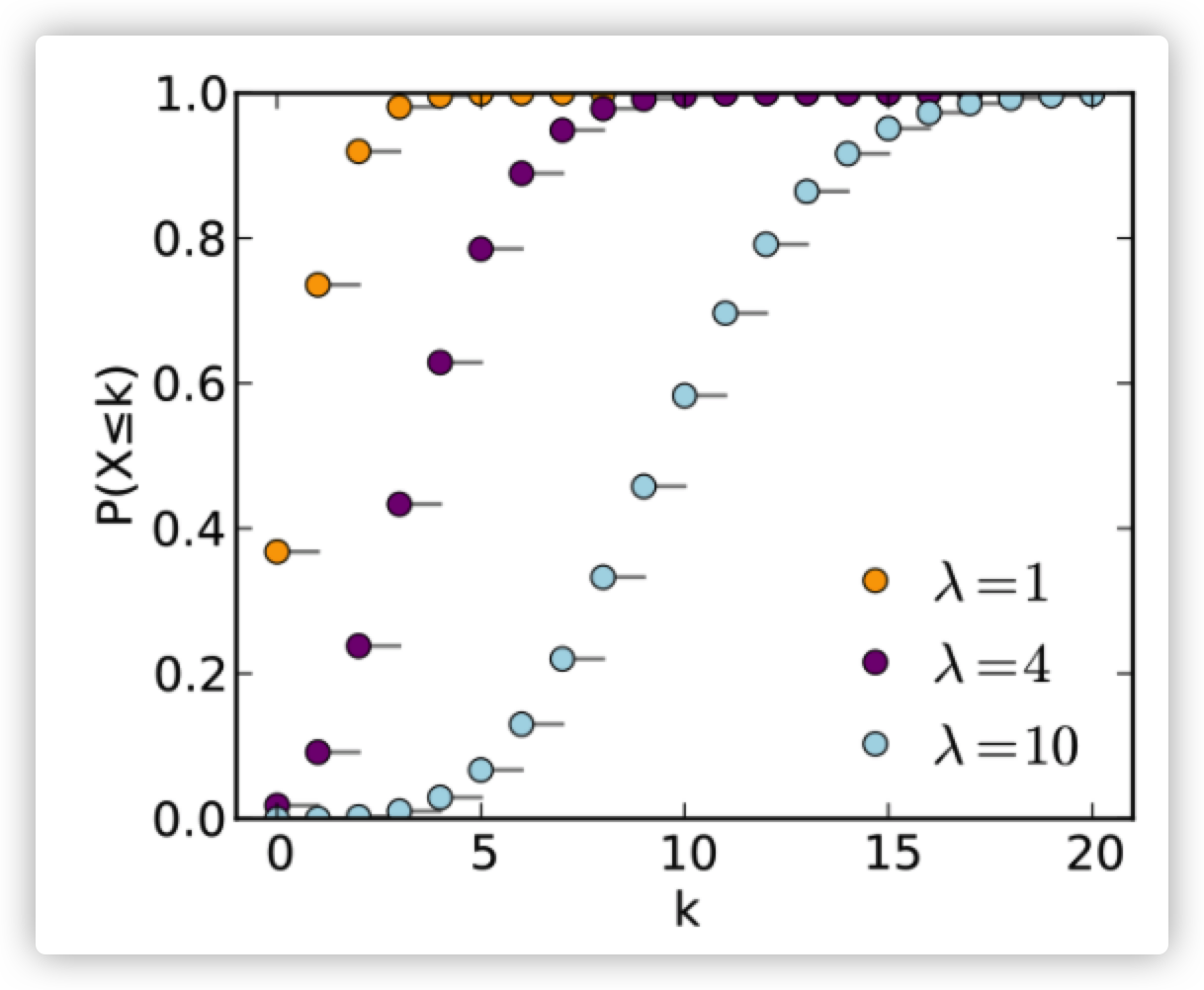
对泊松分布的 CDF作解释：每个点的意义就是单位时间或者面积内随机事件发生的次数小于等于K次发生的概率

期望与方差

求期望很简单，只要提出一个 $\lambda$ 剩下的求和为1；

方差的计算：根据公式 $V(X)= E(X^2)-E(X)^2 = \lambda $

几何分布与负二项分布

几何分布

几何分布：在伯努利试验序列中，记每次试验中事件A发生的概率为p，如果X为事件A首次出现时的试验次数，则X的可能取值为 $1,2\cdots$, 则称 X 服从几何分布，记为 $X\sim Ge(p)$

分布列： $P(X=k)=(1-p)^{k-1}p , ~k=1,2\cdots$

例如，某产品的不合格率为0.05 , 则首次查到不合格品的检查次数 $X\sim Ge(0.05)$

性质：无记忆性

设 $X\sim Ge(p)$ ,则对任意正整数m与n有： $P(X>m+n|X>m)=P(X>n)$

这个定理表明，在前m次试验中事件A没有出现的条件下，在接下去的n次试验中A仍然不出现的概率只与n有关，而与以前的m次试验无关，似乎忘记了前面m次的试验结果，这就是无记忆性。

期望与方差

期望:

令 $1-p = q$

$E(X)=p+2qp+3q^2p\cdots+kq^{k-1}p = p(1+2q+3q^2+\cdots+kq^{k-1})$

令括号内部的式子为 $f(q)$, 则 $f(q)=(q+q^2+\cdots+q^k)’=[\frac{q(1-q^k)}{1-q}]’$

当$k\rightarrow \infty$的时候， $q^k\rightarrow 0$ ，因此 $[\frac{q}{1-q}]’ = \frac{1-q+q}{(1-q)^2}=\frac{1}{p^2}$

所以 $E(X)=\frac{1}{p}$

方差：

根据公式 $V(X)=E(X^2)+E(X)^2$计算，方法和求期望一样。解得 $V(X)=\frac{1-p}{p^2}$

负二项分布

作为几何分布的一种延伸，我们来讲负二项分布，也叫做帕斯卡分布

如果X 为事件 A 第 r 次出现时的试验次数，则 X的可能取值为 $r,r+1,\cdots,r+m,\cdots$ , 称 X 服从负二项分布。

分布列： $P(X=k)=C_{k-1}^{r-1}p^r(1-p)^{k-r} , k=r,r+1,\cdots$

记为： $X\sim Nb(r,p)$ 当 r=1 时，即为几何分布。

一个负二项分布可以写成 r 个独立同分布的几何分布的和的形式

期望与方差

一个负二项分布可以写成r个独立同分布的几何分布的和的形式，因此其期望可以写作 $\frac{r}{p}$, 方差则可以写作$r(1-p)/p^2$

常用连续分布

正态分布(高斯分布)

在统计学中常常用正态分布，在机器学习领域常常叫高斯分布。

若随机变量 X 的密度函数为 $p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{(x-\mu)^2}{2\sigma^2}},-\infty<x<\infty$，则称 X 服从正态分布，称X为正态变量

记作 $X\sim N(\mu,\sigma^2)$ 其中参数 $-\infty<\mu<\infty , \sigma>0$

密度函数(PDF) p(x):

分布函数(CDF) $p(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^xe^{\frac{(t-\mu)^2}{2\sigma^2}}dt$

标准正态分布

当 $\mu =0,\sigma^2 =1 $ 时候。通常记标准正态变量为U，记标准正态分布的密度函数为 $\varphi(u)$即：

$ \varphi(u)=\frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}, -\infty<u<\infty$

分布函数为 $\Phi(u)$

$\Phi(u)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^u e^{-\frac{t^2}{2}}dt, -\infty<u<\infty$

由于标准正态分布的分布函数不含任何未知参数，故其值 $\Phi(u)=P(U\leq u)$ 完全可以算出。对于 $\Phi(u)$ 有

$\Phi(-u)=1-\Phi(u)$
$P(U>u)= 1-\Phi(u)$
$P(a<U<b)=\Phi(b)-\Phi(a)$
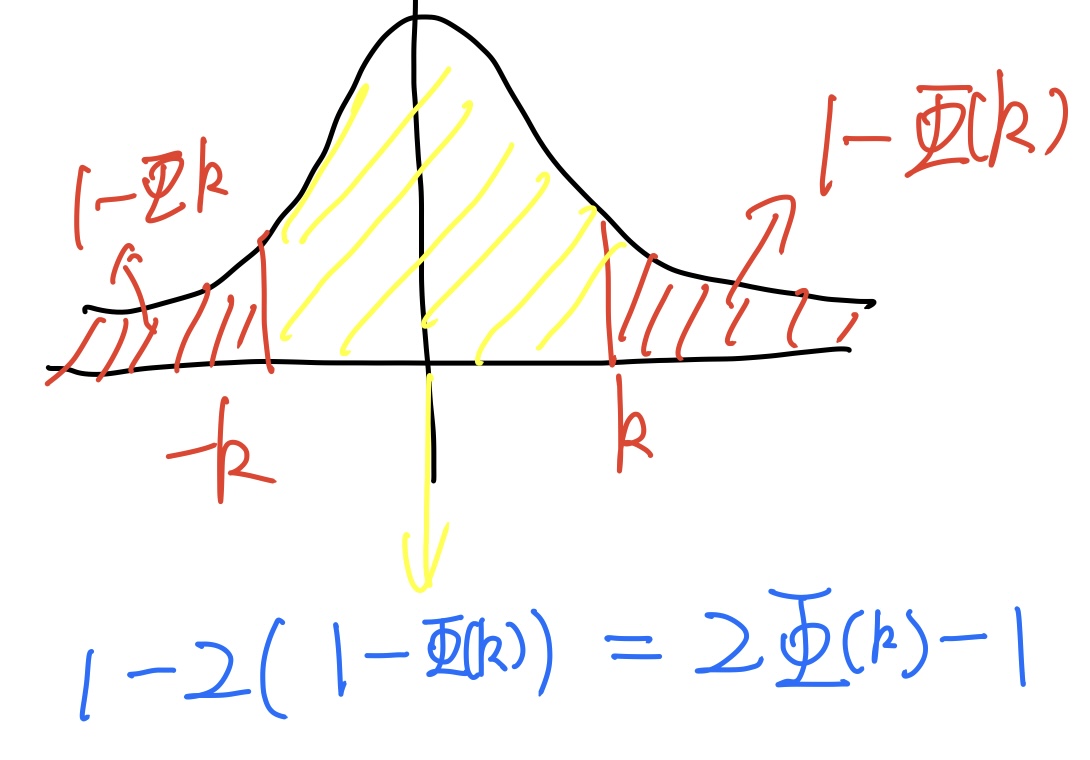
$P(|U|<c)=2\Phi(c)-1$ ，原理如下图所示，黄色阴影部分即为 $P(|U|<c)$

正态分布族

正态分布有一个家族： $\mathcal P = {N(\mu,\sigma^2):-\infty < \mu<\infty ,\sigma >0 } $,标准正态分布也是其中的一员. 一般的正态变量都可以通过一个线性变换(标准化) 化成标准正态变量。因此与正态变量有关的一切事件的概率都可以通过查标准正态分布函数表来获得。

定理： 若随机变量 $X\sim N(\mu,\sigma^2)$ ,则 $U=(X-\mu)/\sigma\sim N(0,1)$

由以上的定理，我们可以得到一些在实际中有用的计算公式: 若随机变量 $X\sim N(\mu,\sigma^2)$ ,则：

$P(X\leq c) = \Phi(\frac{c-\mu}{\sigma})$

例题：设随机变量 X服从正态分布 $N(108,3^2)$ , 试求：1. $P(102<X<117)$ 2. 常数a，使得 $P(X<a)=0.95$

我们可以利用公式 $P(a<U<b)=\Phi(b)-\Phi(a)$ 可得： $P(102<X<117)=P(117)-P(102)=\Phi(\frac{117-108}{3})-\Phi(\frac{102-108}{3})=\Phi(3)-\Phi(-2)=0.9759$

对于2，我们首先对定理做一个变形：由 $P(X<a)=\Phi(\frac{a-108}{3})= 0.95$ 可知： $\Phi^{-1}(0.95)=\frac{a-108}3$

所以现在我们就要查出满足$\Phi(x)=0.95$ 的值。通过查表得： $\Phi(1.64)=0.9495,\Phi(1.65)=0.9505$ ,再用线性内插法可得 $\Phi(1.645)= 0.95$ 即 $\Phi^{-1}(0.95)=1.645$ 故：$\frac{a-108}{3} = 1.645$ 解得 $a=112.935$

例题：

设随机变量X 服从正态分布 $N(\mu,\sigma^2)$ 试问：随着 $\sigma$ 的增大，概率 $P(|X-\mu|<\sigma)$ 是如何变化的？

这个例题也可以作为一个正态分布的性质来记：

$P(|X-\mu|<\sigma)=P(-\sigma <X-\mu<\sigma)=P(-1<\frac{X-\mu}{\sigma}<1)$

由 $\frac{(X-\mu)}{\sigma}\sim N(0,1)$可知，$P(-1<\frac{X-\mu}{\sigma}<1)=\Phi(1)-\Phi(-1)$

因此，不管 $\sigma$如何变化， $P(|X-\mu|<\sigma)$的值都是个定值。

$3\sigma$ 原则

设随机变量 $X\sim N(\mu,\sigma^2)$ , 则 $p(\mu-k\sigma<X<\mu+k\sigma)=P(|\frac{X-\mu}{\sigma}|<k) = \Phi(k)-\Phi(-k)=2\Phi(k)-1$

当 $k=1,2,3$ 时，有

$P(\mu-\sigma<X<\mu+\sigma) = 2\Phi(1)-1 = 0.6826\\ P(\mu-2\sigma<X<\mu+2\sigma) = 2\Phi(1)-1 = 0.9545\\ P(\mu-3\sigma<X<\mu+3\sigma) = 2\Phi(1)-1 = 0.9973$

这是正态分布的重要性之，计入某随机变量的取值概率近似满足上面三个公式，则可认为这个随机变量近似服从正态分布。三式中有一个偏差较大，则可认为这个随机变量不服从正态分布。这就是 $3\sigma$ 原则。这个原则在 X 的观察值较多的时候常常用于判断 X 的分布是否近似服从正态分布

期望

由期望的定义可以知道， $E(X)=\int_{-\infty}^{\infty}\frac{x}{\sigma\sqrt{2\pi}}exp{-\frac{(x-\mu)^2}{2\sigma^2}}dx$

令 $y=x-u$ 可得： $E(X)=\int_{-\infty}^{\infty}y\frac{1}{\sigma\sqrt{2\pi}}exp{-\frac{y^2}{2\sigma^2}}dy+u\frac{1}{\sigma\sqrt{2\pi}}exp{-\frac{y^2}{2\sigma^2}}$

第一部分用 $I1$ 表示：因为$\int{-\infty}^{\infty} = x\frac{1}{\sigma\sqrt{2\pi}}exp{-\frac{x^2}{2\sigma^2}}$ 是一个奇函数，所以第一部分等于0

所以原式可以写成 $E(X)=\mu\int_{-\infty}^{\infty}\frac{1}{\sigma\sqrt{2\pi}}exp{-\frac{x^2}{2\sigma^2}}$

后面的积分就是求 $\int_{-\infty}^\infty N(0,\sigma^2)dx = 1$

因此$E(X)=\mu$

方差

均匀分布

当分布函数(CDF)为：$F\left( x\right) =\begin{cases}0,~~x <a\ \dfrac{x-a}{b-a},~~a\leq x\leq b\ 1,~~x >b\end{cases}$，密度函数(PDF)为$\begin{cases}\dfrac{1}{b-a},a <x <b\ 0, {其他}\end{cases}$时，这个分布就是区间 $(0,a)$上的均匀分布，记为 $U(a,b)$

期望和方差

$E(X) = \int_a^b x \frac{1}{b-a}dx = \frac{a+b}{2}$

$Var(X) = E(X^2)-E(X)^2 = (b-a)^2/12$

指数分布

若随机变量X的密度函数(PDF)为$p(x) = \begin{cases}\lambda e^{-\lambda x} , x \geq 0 \ 0, x<0 \end{cases}$ 则称 x 服从指数分布。记作 $x\sim exp(\lambda)$ ,其中参数 $\lambda>0 $ .

正则性的验证：$\int_0^{+\infty} p(x) dx = -e^{-\lambda x}|_0^{\infty} = 1$

指数分布的分布函数为： $F(x)=p(X\leq x) =\begin{cases}1- e^{-\lambda x} , x \geq 0 \ 0, x<0 \end{cases}$

指数分布是一种偏态分布，由于指数分布随机变量值可能取非负实数，所以指数分布常用作各种“寿命” 分布。比如说电子元器件的寿命、动物的寿命、通话时间都可以假定服从指数分布。

指数分布的 PDF:

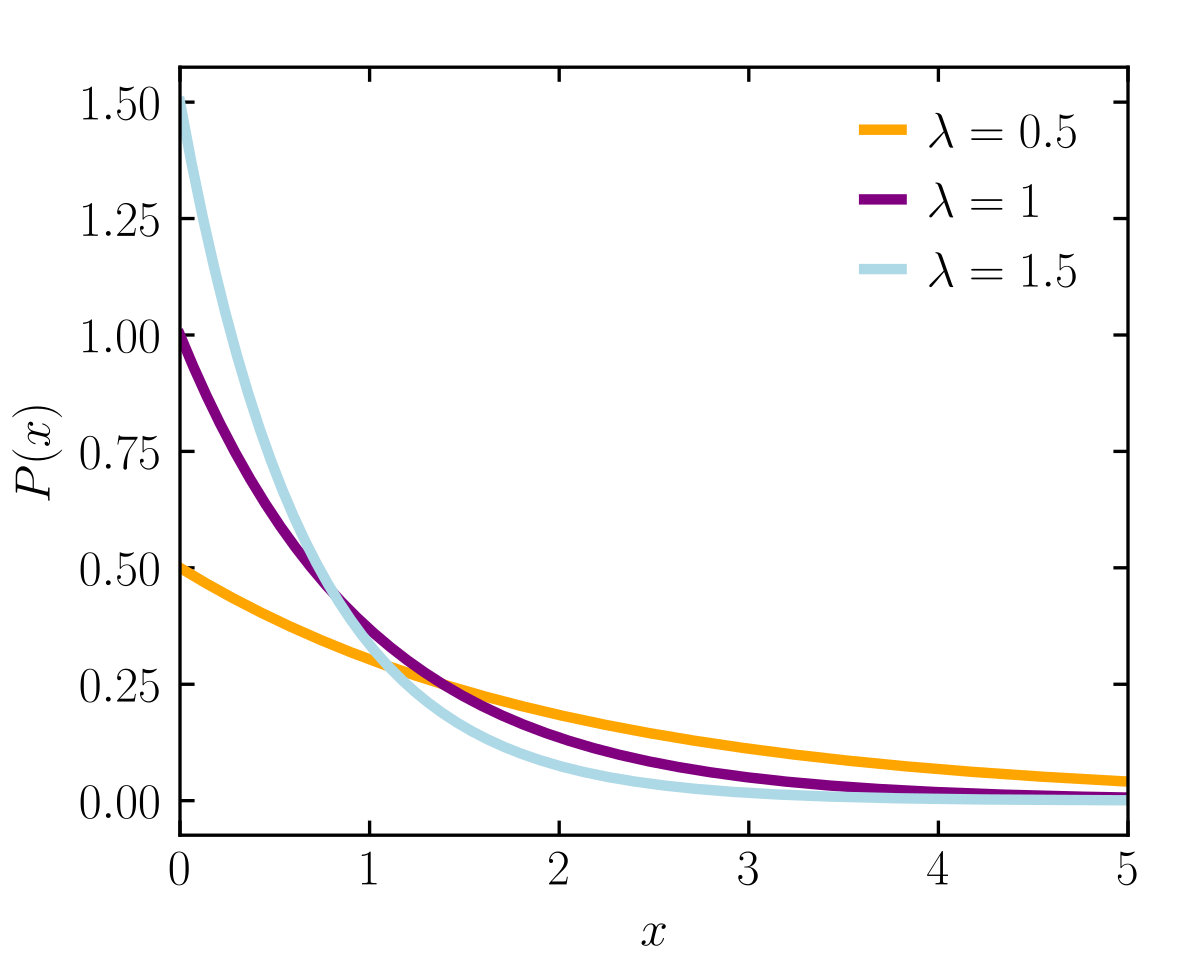
先来看 $\lambda = 1$ 这条曲线。曲线上横坐标为1的点，其意义是 1个单位时间该发生1次的概率。如果横坐标为2，其意义就是2个单位时间内发生1次的概率。抽象一点来说就是：第 k 次改时间发生后隔2个单位时间发生第 $k+1$ 次该事件的概率。

当 $\lambda = 1.5$ 的时候，变得更加抽象了，因为这时候横坐标为1的点其意义是1个单位的时间内发生1.5次的概率。换个说法就是第k次事件发生后1个单位时间内该事件发生1.5 次的概率。

指数分布的 CDF：

性质

无记忆性

和几何分布一样，指数分布有着无记忆性。也就是说,对任意的$s,t >0$, 若$X\sim Exp(\lambda)$ ,则 $P(x>s+t|x>s)=P(x>t)$ .

放到一个具体的例子中，可以理解为：记X 为某种产品的使用寿命(h) 。若X服从指数分布，那么已知此产品使用了 s(h)没有发生故障，则再能使用 t(h) 而不发生故障的概率与已使用的 $s(h)$无关，只想到与重新开始使用 t(h) 的概率。

和泊松分布的关系

如果某设备在长为t的时间 $[0,t]$ 内发生故障的次数 $N(t)$ (与时间长度t有关)服从参数为 $\lambda t$ 的泊松分布。则相继两次故障之间的时间间隔T服从参数为$\lambda $ 的指数分布。

期望和方差

由指数分布和伽马分布的关系可以知道，指数分布的期望和方差即为当$\alpha = 1$ 的时候伽马分布的期望和方差。

所以 $E(X) = \frac{1}{\lambda},Var(X) = \frac{1}{\lambda^2}$

泊松分布是针对随机事件发生次数的定义的离散随机变量，而指数分布是针对随机事件发生的间隔时间定义的连续随机变量，这是二者最大的区别。切莫因为参数λ把二者混淆了

伽马分布

伽马函数

首先我们来定义伽马函数

$\Gamma(\alpha) = \int_0^\infty x^{\alpha-1}e^{-x} dx$ 是伽马函数。其中 $\alpha>0 $ 。

函数性质

$\Gamma(1)=1,\Gamma(\frac{1}{2}) = \sqrt{\pi}$

当 $\alpha$ = 0.5 时， $\Gamma(\frac{1}{2} ) = \int_0^\infty\frac{e^{-x}}{\sqrt{x}}dx$ , 令 $t = \sqrt x$ 则 $x = t^2$ 原式等于 $2\int_0^\infty e^{-t^2}dt$

根据正态分布的密度函数可以知道，当 $\mu = 0,\sigma^2= \frac{1}{2}$ 时， $1 = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi \frac{1}{2}}} exp(\frac{-(t-0)^2}{2\frac{1}{2}})dt$

$\int_{-\infty}^{\infty} \frac{1}{\sqrt\pi}*e^{-t^2}dt = 1 $ 又正态分布为偶函数，因此可得 $\Gamma(\frac{1}2)=\sqrt{\pi}$

$\Gamma(\alpha+1) = \alpha\Gamma(\alpha) $ (可用分布积分法证明得到)，当 $\alpha$为自然数 n的时候，有 $\Gamma(n+1) = n\Gamma (n)= n!$

伽马分布

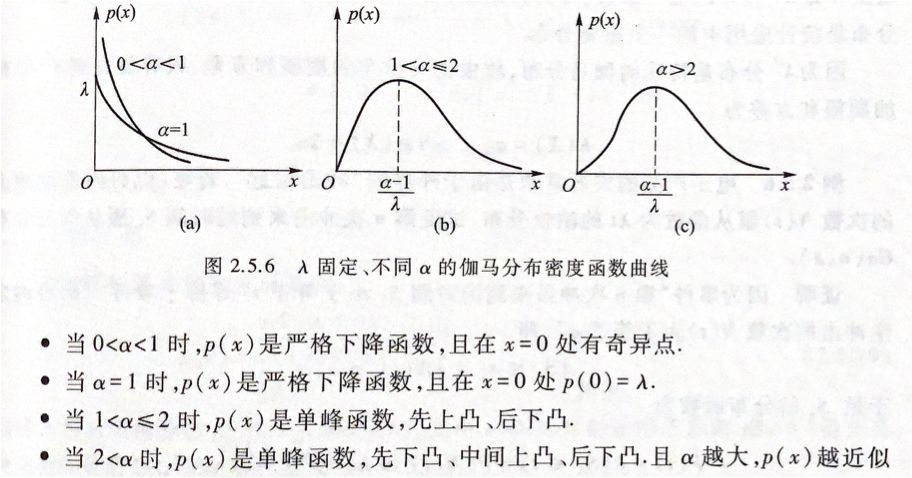
若随机变量X的密度函数为 $p(x) = \begin{cases}\frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x} , x \geq 0 \ 0, x<0 \end{cases}$ 则称 x 服从伽马分布，记作 $x\sim ga(\alpha ,\lambda)$ 其中，$\alpha>0 $ 为形状参数，$\lambda>0$ 是尺度参数。如下图所示

性质

当伽马函数的 $\alpha = 1$ 的时候，伽马分布的PDF = 指数分布的PDF。这说明指数分布是特殊的伽马分布

期望

首先我们要牢记这条性质：$\Gamma(\alpha+1) = \alpha\Gamma(\alpha) $

$E(X) = \int_0^\infty xp(x)dx = \int_0^\infty x\cdot\frac{\lambda^\alpha}{\Gamma{(\alpha)}}x^{\alpha-1}e^{-\lambda x}dx = \frac{\lambda^\alpha}{\Gamma(\alpha)}\int_0^\infty x^{(\alpha+1)-1} e^{-\lambda x}dx $

$=\frac{\lambda^\alpha}{\Gamma(\alpha)}\frac{\Gamma(\alpha+1)}{\lambda^{\alpha+1}}1 = \frac{\alpha}{\lambda}$

我们可以利用凑数的方法，强行把后面的积分配成一个 $Ga(\alpha+1,\lambda)$ ,根据 $\int_0^\infty Ga(\alpha+1,\lambda) = 1$可以消除积分。

方差

利用配方法，我们还可以求出伽马分布的方差

我们根据公式 $Var(X) = E(X^2)-E(X)^2$ 可以得到

$E(X^2) = \int_0^\infty x^2 \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}dx =\frac{\lambda^\alpha}{\Gamma(\alpha)} \frac{\Gamma({\alpha+2})}{\lambda^{\alpha+2}}\int_0^\infty Ga(\alpha+2,\lambda)dx = \frac{\alpha(\alpha+1)}{\lambda^2}$

$Var(X) = E(X^2)-E(X)^2 = \frac{\alpha(\alpha+1)}{\lambda^2} - \frac{\alpha^2}{\lambda^2} = \frac{\alpha}{\lambda^2}$

贝塔分布

贝塔函数

称函数 $B(a,b)=\int_0^1 x^{a -1}(1-x)^{b-1}dx$ 为贝塔函数，其中参数$a>0,b>0$

贝塔函数性质

$B(a,b) = B(b,a)$ 通过换元法可以直接证明
贝塔函数和伽马函数之间有关系： $B(a,b) = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}$

贝塔分布

若随机变量X的密度函数为 $p(x) = \begin{cases}\frac{\Gamma (a+b)}{\Gamma(a){\Gamma(b)}}x^{a-1}(1-x)^{b-1 } , 00,b>0$ 都是形状参数，下图给出几种典型的贝塔分布密度函数曲线。

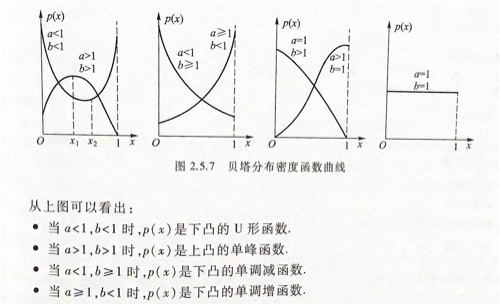
当 a=b=1 时，$Be(1,1) = U(0,1)$ 即贝塔分布等于0-1上的均匀分布

因为服从贝塔分布 $Be(a,b)$ 的随机变量是仅在区间$(0,1)$取值的所以可以描述一些不合格产品率、机器的维修率、市场的占有率、射击的命中率等各种比率。

期望和方差

同样的，我们可以利用求伽马分布的期望和方差的办法来求贝塔函数的期望和方差。

$P(X) =\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} x^{a-1}(1-x)^{b-1}$

$E(X) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\int_0^1 x^{(a+1)-1}(1-x)^{b-1} dx= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\frac{\Gamma(a+1)\Gamma(b)}{\Gamma(a+b+1)} = \frac{a}{a+b}$

$Var(X) = E(X^2)-E(X)^2 = \frac{(a+1)a}{(a+b+1)(a+b)}- \frac{a^2}{(a+b)^2} = \frac{ab}{(a+b+1)(a+b)^2}$

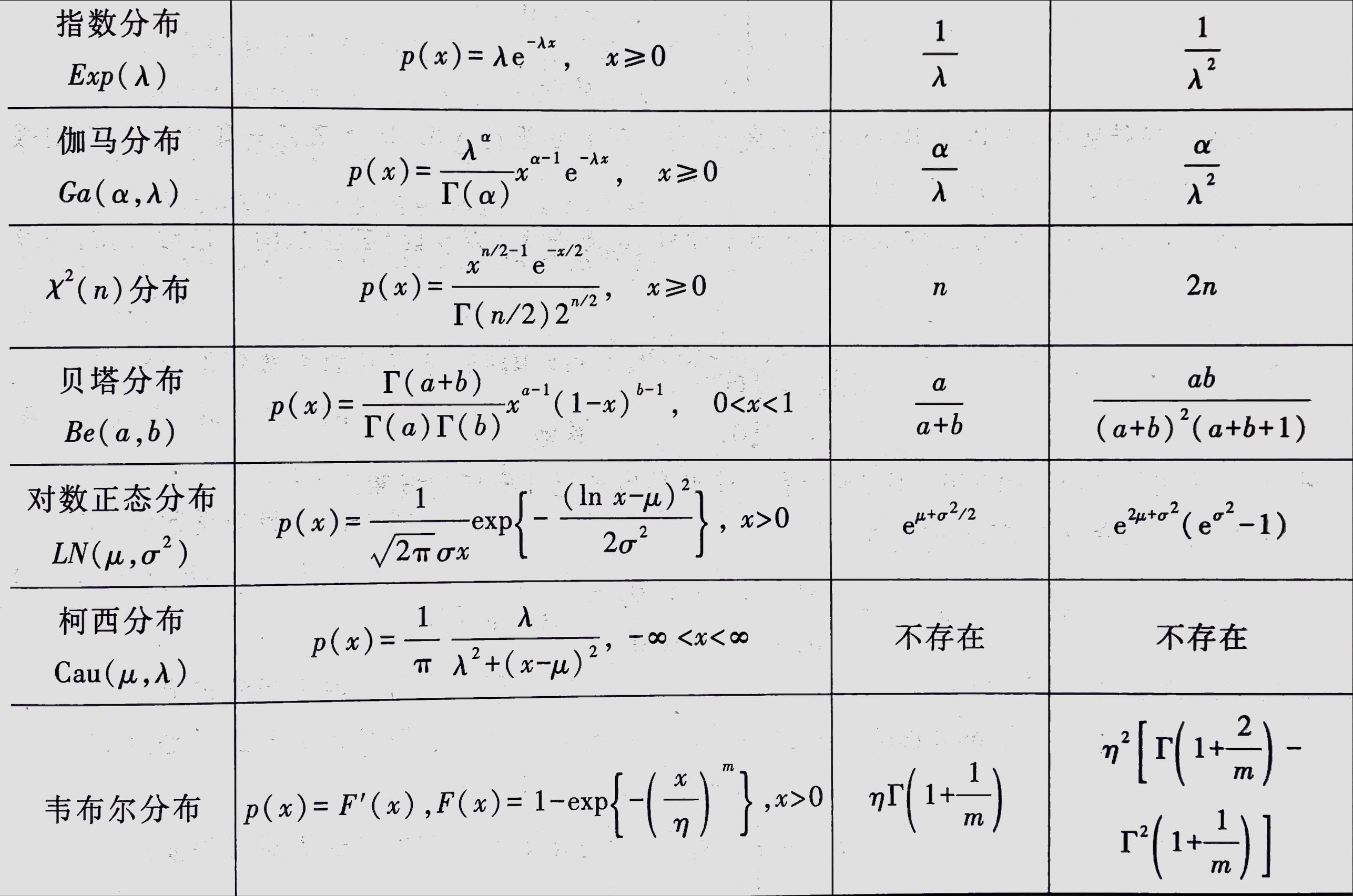
常用概率分布表格

随机变量函数的分布

离散随机变量函数的分布

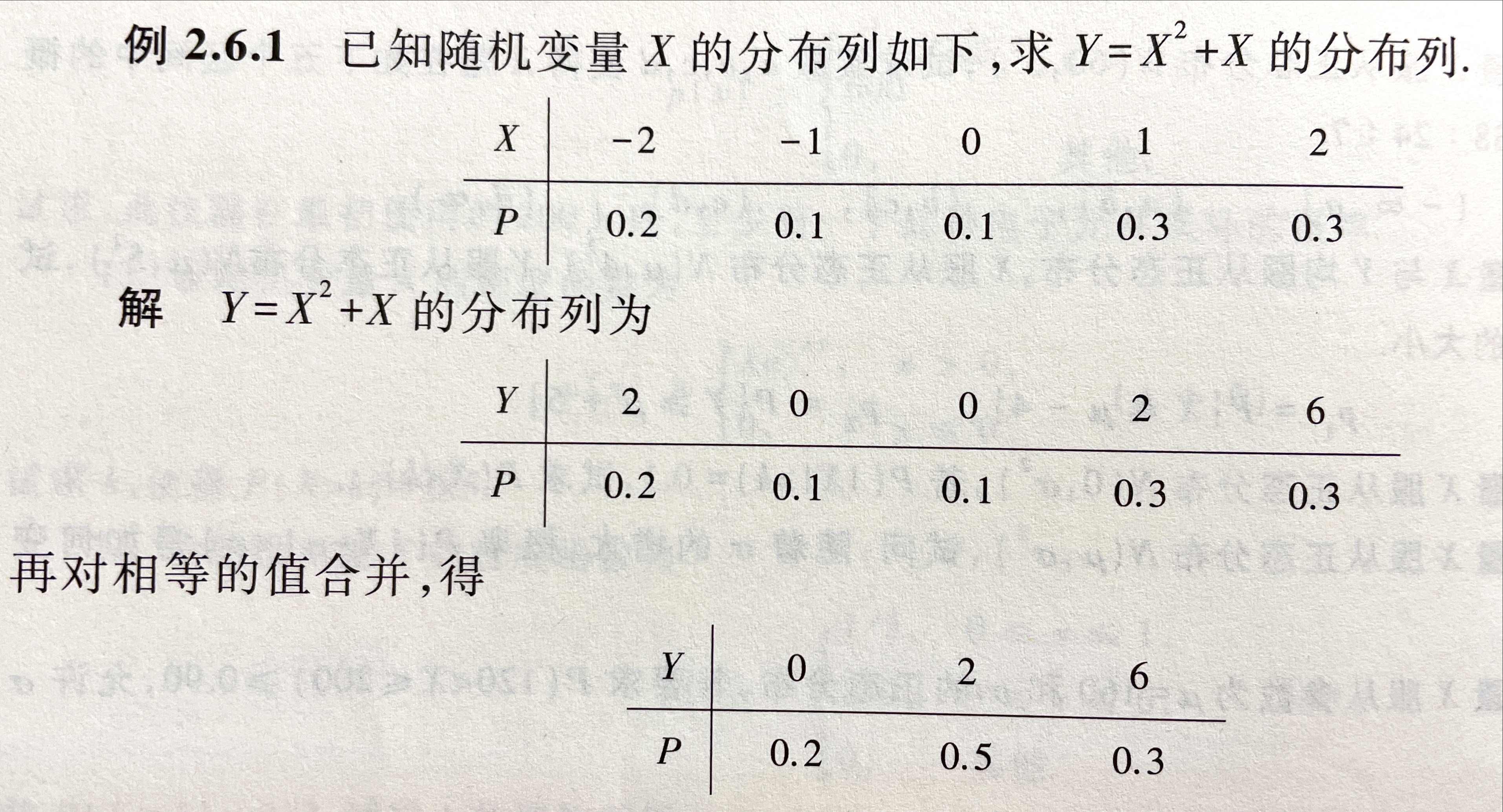
这种情况比较简单，如果题目给出的是X的分布列，那么我们直接列出$g(x)$的分布列即可。

连续随机变量函数的分布

当 $Y=g(X)$ 为离散随机变量

这种情况比较简单，只要将 Y 的值一一列出，再讲 Y 取各种可能值得概率求出来即可。例如：设 $X\sim N(\mu,\sigma^2)$

$Y = \begin{cases}0 , X<\mu \ 1, X\geq \mu \end{cases}$ 这样计算很容易： Y 服从 $p=0.5$的0-1分布

因此，我们要注意一些 pdf 为对称函数的分布，会简化很多计算。

比如说 $X$的pdf为 $p(x)=\frac{2}{\pi}\cdot \frac{1}{e^x+e^{-x}} ,-\infty<x<\infty$ ,试求 $Y=g(X)$ 的分布， $g(X) = \begin{cases}-1 , x<0 \ 1, x\geq 0 \end{cases}$

p(x)就是一个很标准的偶函数，关于x=0对称。因此 Y = 1和-1 的概率相等，都是0.5

当 $g(x)$ 在定义域内为严格单调函数时

定理1

设 $X$ 是连续随机变量，其密度函数为 $p_X(x)$ $Y=g(x)$ 是另一个连续随机变量。若 $y=g(x)$ 严格单调，其反函数 $h(y)$ 有连续导函数，则$Y=g(X)$ 的密度函数为：

$p_Y(y)= \begin{cases} P_X(h(y))|h’(y)| ,~a<y<b \ 0, 其他 \end{cases}$ 其中 $a=min{g(-\infty).g(\infty)}$ , $b=max{g(-\infty),g(\infty)}$

例题：

设随机变量X服从区间$(1,2)$上的均匀分布，试求 $Y=e^{2X}$ 的密度函数

步骤1：写出 X 的 pdf

$p_X(y)= \begin{cases} 1 ,~~1<y<2 \ 0, 其他 \end{cases}$

步骤2：写出Y与X之间的关系Y=g(x)

这里我们已经知道了 $y=e^{2x}$

步骤3：判断g(x)是否在定义域内为单调递增函数

$y=e^{2x}$在 $x\in(1,2)$ 内是严格的单调递增函数

步骤4：计算g(x)的反函数h(x)以及 |h’(y)|

求得 $x=\frac{1}{2}\ln y$

步骤5：根据公式，计算 $p_Y(y)=p_X(h(y))|h’|$

$p_Y(y) =\begin{cases} 1\cdot \frac{1}{2y}, e^2<y<e^4 \ \0 ~~其他 \end{cases}$

根据以上定理，我们可以来证明几个很有用的结论，并用定理形式表示。

定理2

设随机变量 X 服从正态分布 $N(\mu,\sigma^2)$ ，则当 $a\neq 0$ 时候，有 $Y=aX+b\sim N(a\mu+b,a^2\sigma^2)$

我们可以通过分类讨论来证明 $p_Y(y)=\frac{1}{\sqrt{2\pi}(a\sigma)}{exp{-\frac{(y-a\mu-b)^2}{2a^2\sigma^2}}}$ ,也就是 $N(a\mu+b,a^2\sigma^2)$ 的密度函数。

我们可以直接用期望和方差来计算 $\mu$值和$\sigma^2$值

定理3：对数正态分布

设随机变量 $X\sim N(\mu,\sigma^2)$

令 $Y=e^X$ ，那么当$y>0$ 时，Y 的密度函数为：

$p_Y(y) = \frac{1}{\sqrt{2\pi}\sigma}\exp\{-\frac{(\ln y-\mu)^2}{2\sigma^2}\}\frac{1}{y} = \frac{1}{\sqrt{2\pi}y \sigma} \exp\{-\frac{(\ln y-\mu)^2} {2\sigma^2}\}$

$p_Y(y)= \begin{cases}\frac{1}{\sqrt{2\pi}y\sigma}exp{-\frac{(\ln y-\mu)^2}{2\sigma^2}} , y>0 \ 0, y\leq 0 \end{cases}$

这个分布被称为正态分布，记为 $LN(\mu,\sigma^2)$ ,其中 $\mu$ 称为对数均值，$\sigma^2$ 称为对数方差。对数正态分布 $LN(\mu,\sigma^2)$ 是一个偏态分布，也是一个常用分布，实际种有不少随机变量服从对数正态分布。

对数函数的证明：

绝缘材料的寿命服从对数正态分布
设备故障的维修时间服从对数正态分布

对数正态分布的期望

$E(Y)=E(\exp\{X\})=\int_{-\infty}^\infty\exp\{x\}\frac{1}{\sqrt {2\pi}\sigma} \exp\{-\frac{1}{2\sigma^2}(x-\mu)^2\}dx\\~\\ =\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}\sigma}\exp\{-\frac{1}{2\sigma^2}(x^2-2\mu x-2\sigma^2x+\mu^2)\}dx\\ ~\\ =\int_{-\infty}^\infty\frac{1}{\sqrt{2\pi}\sigma}\exp\{-\frac{1}{2\sigma^2}(x-\mu-\sigma^2)^2+\frac{(\mu+\sigma^2)^2}{2\sigma^2}-\frac{\mu^2}{2\sigma^2}\}dx\\ =\exp\{\mu+\sigma^2/2\}$

给定$N(0,1)$的p分位数为$\mu_p$ ,求Y的p分位数 $y_p$

已知

$p=P(Y\leq y_p)=P(\exp\{X\}\leq y_p)=P(X\leq \ln(y_p))=P(\frac{X-\mu}{\sigma}\leq\frac{\ln(y_p)-\mu}{\sigma})\\$

因为 $X\sim N(\mu,\sigma^2)$, 所以 $\frac{X-\mu}{\sigma}\sim N(0,1)$ ，于是：

$\frac{ln(Y_p)-\mu}{\sigma}=\mu_p$

因此，$y_p=\exp{\sigma\mu_p+\mu}$

定理4

设随机变量 X 服从伽马分布 $Ga(\alpha,\lambda)$ ，则当 $k>0$的时候，有 $Y=kX\sim Ga(\alpha,\lambda/k)$

根据定理1可得， $p_Y(y)=p_x(\frac{y}k)\frac{1}{k} = \frac{\lambda^\alpha}{k\Gamma{(\alpha)}} (\frac{y}{k})^{\alpha-1} exp{-\lambda \frac{y}{k}}$

=$\frac{(\lambda/k)^\alpha}{\Gamma(\alpha)}y^{\alpha-1} exp{-\frac{\lambda}{k}y}$ 这也就是 $Ga(\alpha,\lambda/k)$ 的密度函数。

定理5

若随机变量 X的分布 $F_X(x)$ 为严格单调增的连续函数，其反函数 $F_X^{-1} (y)$ 存在，那么 $Y=F_X(X)$服从(0,1)上的均匀分布 $U(0,1)$

这个定理比较神奇，我们来看一下它的证明：

由于分布函数 $F_X(x)$ 仅在 $[0,1]$区间上取值，因此当 $y<0$ 时，因为 ${F_X(X)\leq y}$ 是不可能事件，所以 $F_Y(y) = P(Y\leq y)=P(F_X(X)\leq y)=0$

当 $0\leq y<1$ 有 $F_Y(y) = P(Y\leq y) = P(F_X(X)\leq y)=P(X\leq F_X^{-1}(y))=F_X(F_X^{-1}(y))=y$

当 $y\geq 1$ 时，因为 ${F_Y(y) \leq y)}$是必然事件所以 $F_Y(y)=1$

这个定理表明: 均匀分布在连续分布类中占有特殊地位，任一个连续随机变量 X 都可通过其分布$F(x)$ 与均匀分布随机变量 $U$ 发生关系，譬如 X 服从指数分布, 其分布函数 $F(x)= 1-e^{-\lambda X}$ .当 x 换为 X 后，有 $U=1-e^{-\lambda X}$ 或者 $X=\frac{1}{\lambda}\ln\frac{1}{1-U} $

后一式表明：由均匀分布 $U(0,1)$ 的随机数 $u_i$ 可得指数分布$Exp(\lambda)$ 的随机数 $x_i=\frac{1}{\lambda}ln(\frac{1}{1-u_i}),i=1,2,\cdots,n,\cdots$ 而均匀分布随机数在任何一个统计软件中都可以产生，从而指数分布的随机数也可以获得。

各种分布随机数的获得，就是进行蒙特卡洛法的基础

$g(x)$ 为其他形式时

如果g(x)不是严格单调的函数，那么可直接由分布函数 $F_Y(y)=P(g(X)\leq y)$出发，按函数$g(x)$ 的特点作个案处理，比如：

设随机变量X 服从标准正态分布 $N(0,1)$，试求 $Y=X^2$ 的分布函数函数

步骤1：求 Y 的取值范围

首先 $Y=X^2$,x的取值范围为$(-\infty,+\infty)$ ,则 y的取值范围为 $[0,\infty)$

那么我们就可以先确定当 $y\leq 0$ 的时候，有 $F_Y(y)=0$ ，从而$P_Y(y)=0$

步骤2：根据定义求解。 $F_Y(y)=p_X(Y\leq y)=p_X(g(x)\leq y)$

当 $y>0$ 的时候，有 $F_Y(y)=p_X(Y\leq y)=p_X(X^2\leq y)=p(-\sqrt y\leq X\leq \sqrt y)=2\Phi(\sqrt y)-1$

因此 $Y$ 的分布函数为 $F_Y = \begin{cases}2\Phi(\sqrt y)-1 , y>0 \ 0, y\leq 0 \end{cases}$

分布的其他特征数

k阶矩

定义： 设 X 为随机变量，k为正整数。若数学期望$E(X)$ 存在，则称 $\mu_k = E(X^k)$ 为X的 k阶原点矩。称 $v_k = E(X-E(X))^k$ 为X的k阶中心矩。

显然,一阶原点矩就是数学期望，二阶中心矩就是方差。由1于 $|X|^{k-1} \leq |X|^k+1$, 故 k 阶矩存在时，低于k的各阶矩都存在。

中心矩和原点矩之间有一个简单的关系：

$v_k = E(X-E(X))^k - E(X-\mu_1)^k = \sum_{i=0}^k C_k^i \mu_i(-\mu_1)^{k-i}$

变异系数

当在比较两个随机变量的波动大小的时候，如果仅仅看方差(标准差) 的大小有时会产生不合理的现象。这有两个原因

随机变量的取值有量纲，不同量纲的随机变量用其方差(或标准差)去比较它们的波动大小就显得不合理
在取值的量纲相同的情况下，取值的大小有一个相对性问题，取值较大的随机变量的方差(或标准差)也允许大一些。

因此，要比较两个随机变量的波动大小的时候，在有些场合使用变异系数 来进行比较更有可比性：

若随即变量 X 的二阶矩存在，则称比值：$G_v(X) = \frac{\sqrt{Var(X)}}{E(X)} = \frac{\sigma(X)}{E(X)}$ 为 X 的变异系数。

分位数

设连续随机变量X的分布函数为 $F(x)$ ,密度函数为$p(x)$,对任意 $p\in(0,1)$

满足条件 $F(xp) = \int{-\infty}^{x_p}p(x)dx=p$ 的 $x_p$ 为此分布的 p分位数，又称下侧p分位数；
同理我们称满足条件 $1-F(xp’) = \int{x_p’}^{\infty}p(x)dx=p $ 的 $x_p’$ 为此分布的上侧p分位数
分位数 $x_p$ 是把密度函数下的面积分为两块，左侧面积恰好为p
我们通过标准正态分布p分位数表可以知晓 $\Phi(x)$ 的不同分位数的值$u_p$。然后，对于一般正态分布$N(\mu,\sigma^2)$的p分位数$x_p$ 是方程 $\Phi(\frac{x_p-\mu}{\sigma})= p$ 的解。因此 $x_p = \mu+\sigma u_p$

中位数

设连续随机变量 X 的随机分布为 $F(x)$ ,密度函数为 $p(x)$. 称 $p=0.5$ 时的p分位数$x_{0.5}$ 为此分布的中位数。

$F(x{0.5}) =\int{-\infty}^{x_{0.5}}p(x)dx = 0.5 $

偏度系数

设随机变量 $X$ 的前三阶矩存在，则比值

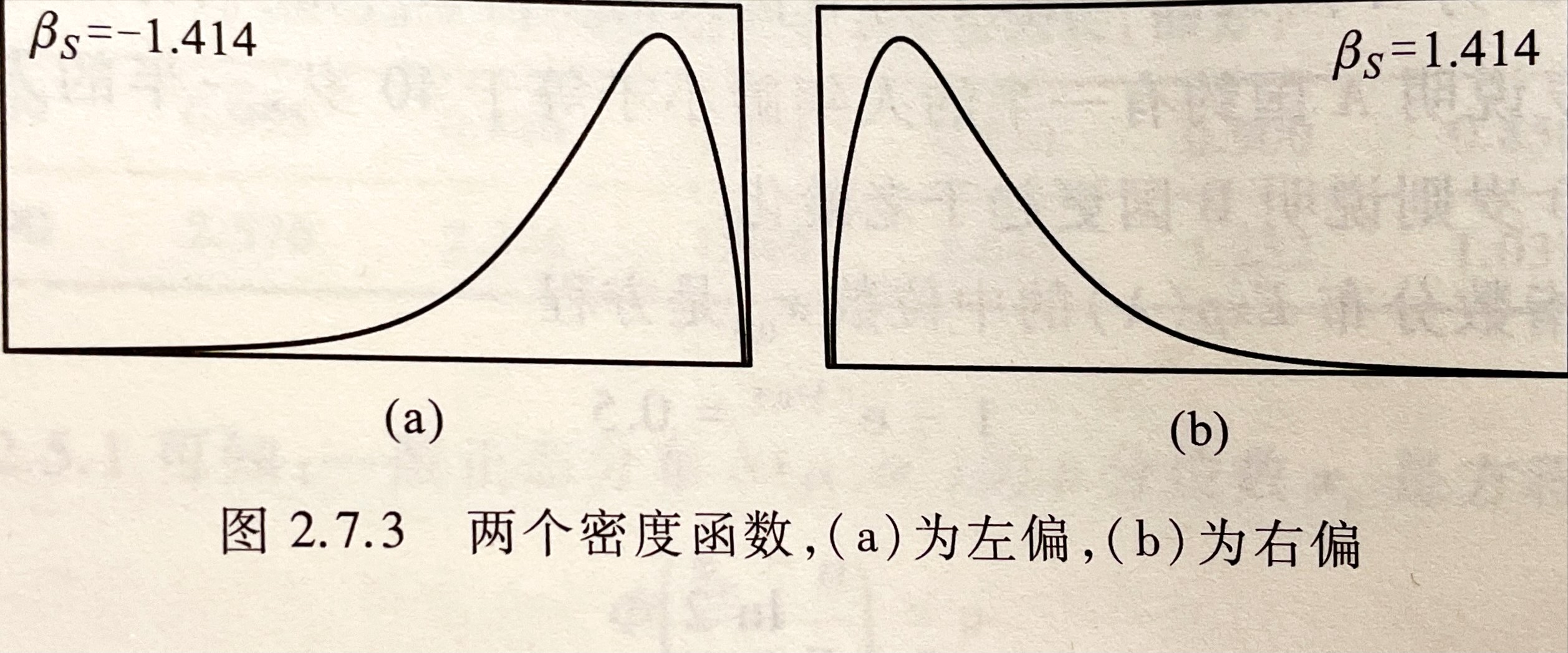
$\beta_S = \frac{v_3}{v_2^{3/2}} = \frac{E(X-E(X))^3}{[Var(X)]^{3/2}}$ 称为 X (或分布) 的偏度系数，简称偏度。当 $\beta_S>0$ 时，称该分布为右偏(正偏)，当 $\beta_S<0$ 时，称该分布为左偏(负偏)。

简单来判断，尾巴偏哪(异常值在哪)就是往哪偏：

峰度系数

设随机变量 X 的前四阶矩存在，则 $\beta_k = \frac{v_4}{v_2^2}-3=\frac{E(X-E(X))^4}{[Var(X)]^2}-3$ 称为X(或分布) 的峰度系数，简称峰度。
峰度时描述分布尖峭程度和尾部粗细的一个特征数
任一正态分布的峰度 $\beta_k =0$ 当 $\beta_k<0$时，分布比正态分布平坦；当$\beta_k>0$时，分布比正态分布更尖峭
偏度与峰度都是描述分布(密度)形状的参数。

z