多维随机变量的特征数
多维随机变量函数的数学期望
当 $y=g(x_1)$ 的时候,我们由第二章的公式可以得出
那么推广到$Y=g(x)=p(x_1,x_2,\cdots,x_n)$ 时
数学期望与方差的运算性质
性质1
设 $(X,Y)$ 是二维随机变量,则有 $E(X+Y)=E(X)+E(Y)$
证明还是比较重要的:
这个性质可以描述为:和的期望等于期望的和。这个性质还可以推广到 n维随机变量场合,即
$E(X_1+X_2+\cdots+X_n)=E(X_1)+E(X_2)+\cdots+E(X_n)$
性质2
若随机变量X与Y相互独立,则有 $E(XY)=E(X)E(Y)$
这个性质可以描述为: 在独立场合,随机变量乘积的数学期望等于数学期望的乘积。
这个性质还可以推广到n维随机变量场合,即若$X_1,X_2\cdots,X_n$ 相互独立,则有
$E(X_1X_2\cdots X_n)=E(X_1)E(X_2)\cdots E(X_n)$
性质3
若随机变量X与Y相互独立,则有 $Var(X\pm Y)=Var(X)+Var(Y)$
这个性质表明: 独立变量代数和方差等于各方差之和。但要注意次性质对标准差不成立。即$\sigma(X\pm Y)\neq \sigma(X)+\sigma(Y)$
标准差只能通“先方差,后标准差”求得,即$\sigma(X\pm Y)=\sqrt{Var(X)+Var(Y)}$
这个性质可以推广到n维随机变量场合 ,即若$X_1,X_2,\cdots,X_n$ 相互独立,则有
$Var(X_1\pm X_2\pm\cdots\pm X_n) = Var(X_1)+Var(X_2)+\cdots+Var(X_n)$
这表明,对独立随机变量来说,它们之间无论是相加还是相减,其方差总是逐个累计起来,只会增加,不会减少。
特别的,当n个相互独立同分布(方差为$\sigma^2$)的随机变量$X_1,X_2,\cdots,X_n )$ 的算术平均的方差为
例题:离散情况
从数字$0,1,\cdots,n$ 中任取两个不同的数字,求这两个数字之差的绝对值和数学期望。
第一步:列出x,y的联合分布列
这里面是从$0\sim n$中取2个不同的数字,那么
第二步:判断是否可以利用期望的性质,如果不能就按照定义求期望,否则可以用性质简化计算
这里是二元随机变量,因此公式可以写为: $\sum_x\sum_yg(x)p(x,y)$
这里还要注意,要我们求得是差的绝对值因此要拆成两部分求和
注意,$\sum_{x=0}^n x^2 = \frac{n(n+1)(2n+1)}{6}$
因此,原式等于:
例题:连续情况
在长为a的线段上任取两个点 $X$ 和 $Y$ ,求此两点间的平均长度
第一步:列出x,y的联合分布
因为X与Y都服从$(0,a)$上的均匀分布,且 X,Y 相互独立,所以$
第二步,判断是否可以利用期望的性质,如果不能就按照定义求期望,否则可以用性质简化计算
这里是二元随机变量,所以公式可写为:$E(g(x))=\int{-\infty}^\infty\int{-\infty}^\infty g(x)p(x,y)dxdy$
要求两点间的平均长度,就是要求$E(|X-Y|)$,
直接求绝对值不太方便,我们拆成两部分,首先将常数 $\frac{1}{a^2}$ 提出
例题:当随机变量是极值分布时
设在区间$(0,1)$上随机取n个点,求相聚最远的两点间的距离的数学期望
第一步,定义极值分布,列出目标期望
分别记 n个点为 $X_1,X_2\cdots,X_n$, 那么这n个点相互独立,且都服从 区间上$(0,1)$的均匀分布$U(0,1) $
所以 $p_X(x)=1,0<x<1; F_X(x)=x$
我们的目的是求 $E(\max{X_1,X_2\cdots,X_n}-\min{X_1,X_2\cdots,X_n})$
因此,我们可以令 $Z=\max{X_1,X_2,\cdots,X_n}, T=\min{X_1,X_2\cdots,X_n}$
根据极值分布的定义,可以分别写出Z和T的分布函数和密度函数:
第二步,判断是否可以利用期望的性质求解
因为求Z和T的联合分布列是比较困难的,因为他们不是独立分布的。所以我们可以利用其性质: $E(X+Y)=E(X)+E(Y)$
分别求$E(Z)$和$E(T)$再相减即可
这个$E(T)$比较难算,我们可以将其配方成一个贝塔分布$Be(2,n)$的积分:
综上,$E(Z-T)=\frac{n}{n+1}-\frac{1}{n+1}=\frac{n-1}{n+1}$
因此,当积分区域确定,积分形状又很类似我们常见的分布的时候,我们可以凑方、配方称常见的分布求积分,会省很多力气。
协方差
设$(X,Y)$是一个二维随机变量,若 $E[(X-E(X))(Y-E(Y))]$存在,则称此数学期望为 $X$ 与 $Y$ 的协方差,或称为$X$ 与 $Y$ 的相关(中心)矩。并记为
特别有 $Cov(X,X)=Var(X)$
- 当$Cov(X,Y)>0$的时候,称 X与Y 正相关, 这时候两个偏差 $(X-E(X))$与 $(Y-E(Y))$ 有同时增加或者同时减少的倾向。由于 $E(X)$与$E(Y)$ 都是常数,故等价于$X$ 与 $Y$ 有同增同减的倾向。
- 当$Cov(X,Y)<0$时,称X与Y负相关 , 这时有X增加而Y减少的倾向,或者有 $Y$增加而$X$减少的倾向。
- 当$Cov(X,X)=0$时,称X与Y不相关,这时候X与Y可能取值毫无关联,也可能是X与Y之间存在某种非线性关系。
性质1
这是常用的协方差计算公式。
$Cov(X,Y)=E(XY)-E(X)E(Y)$
性质2
若随机变量X与Y相互独立,则$Cov(X,Y)=0$ 反之不然。
这是因为在独立场合有 $E(XY)=E(X)E(Y)$ 在,但是如果 $Cov(X,Y)=0$,X与Y可能是不独立的。
比如说,设随机变量 $X\sim N(0,\sigma^2)$,且令 $Y=X^2$ ,则X与Y不独立。 此时 X 与 Y的协方差为 $Cov(X,Y)=Cov(X,X^2)=E(X\cdot X^2)-E(X)E(X^2)=0$
这说明:独立必然导致不相关,而不相关则不一定导致独立。

性质3
对于任意二维随机变量$(X,Y)$有:
因此,这也证明了刚才方差的运算性质。当X,Y互相独立的时候,$Var(X\pm Y)=Var(X)+Var(Y)$
以上的性质还可以推广到更多个随机变量场合,即对任意n个随机变量 $X_1,X_2,\cdots,X_n$有
下面几条性质可以方便协方差的计算
性质4
$Cov(X,Y)=Cov(Y,X)$
即协方差$Cov(X,Y)$的计算与X,Y的次序无关
性质5
$Cov(X,a)=0$
即任意随机变量X与常数a的协方差为0
性质6
性质7
设$X,Y,Z$ 是任意三个随机变量,则
性质8
因为 协方差矩阵是非负定的,其绝对值是大于等于0的,当等于的时候,说明X,Y不相关;当大于0的时候,上述式子成立
例题:常规方法求 Var(g(x,y))
设二维随机变量$(X,Y)$的联合密度为
试求$Var(2X-3Y+8)$
思路
- 展开,化简为独立的X方差与Y方差、协方差形式
- 分别计算 $Var(X),Var(Y)$ ,用到 $Var(X)=E(X^2)-E(X)^2$ 这个公式
- 计算 $E(X),E(X^2),E(Y),E(Y^2)$
- 计算$E(XY)$ 可以从联合密度函数导出
- 计算协方差 $Cov(X,Y)=E(XY)-E(X)E(Y)$
例题:利用常见分布求期望和方差
随机变量$(X,Y)$服从以点$(0,1),(1,0),(1,1)$ 为顶点的三角形区域上的均匀分布,试求$E(X+Y)$和 $Var(X+Y)$
刚开始我用传统方法求解$E(X+Y)$,也就是先求出$p(x,y)$ 然后利用定义求解。但是这种方法对$Var(X+Y)$ 却起不到便利。因此我们可以用一下这种方法:
第一步,求p(x,y)联合分布
第二步,求x,y的边际分布
第三步,用常见的分布求X、Y的期望与方差
$p_X(x)=2x$ 可以看成 $p(x)=\frac{\Gamma(2+1)}{\Gamma(2)\Gamma(1)} x^{2-1}(1-x)^{1-1}$, 因此 $X\sim Be(2,1)$ ,同理 $Y\sim Be(2,1)$
因此
第四步:先计算E(X+Y)
由性质可以得到
第五步:计算Var(X+Y)
首先,列出$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$
因此我们还要求$Cov(X,Y)=E(XY)-E(X)E(Y)$
因为X,Y并不是互相独立的,因此还要计算 $E(XY)$,$E(XY)$可以用传统方法求解:
因此
这里我们要记住,贝塔分布 $Be(2,1)=2x$ 这一个很隐蔽但是很有用的性质。
例题3-1:极值分布的期望和方差
设 $X_1,X_2,X_3,X_4,X_5$ 是独立同分布的随机变量,其共同的密度函数
试求 $Y=\max{X_1,X_2,\cdots,X_5}$ 的密度函数、数学期望、方差
第一步:求出X的分布函数
第二步: 求出Y的分布函数
第三步:求出密度函数、数学期望和方差
例题3-2: 求 E(极值分布)
设X,Y 独立同分布,都服从标准正态分布$N(0,1)$, 求$E(\max{X,Y})$
第一步: 化简 max{X,Y}
现在我们把 $E[\max{X,Y}] $ 转换成了 $\frac{E|X-Y|}{2}$
第二步:写出 X-Y 的密度函数
因为X,Y 独立,都服从 $N(0,1)$根据性质 $X-Y\sim N(0,2)$ ,这里使用了正态分布的可加性——
若随机变量 $X\sim N(\mu,\sigma^2)$ ,则对任意非零实数a有 $aX\sim N(a\mu,a^2\mu^2)$ 。
因此,我们可以得到一个重要结论, 即
若$X_i\sim N(\mu_1,\sigma_1^2),i=1,2\cdots,n$则参数 $\mu_0$与 $\sigma_0^2$ 分别为:
$P(X-Y)=\frac{1}{\sqrt{2\pi}\sqrt{2}}\exp{-\frac{(x-y)^2}{4}}$
第三步:根据定义计算期望
令 $X-Y=t$. 则
因此 $E[\max{X,Y}]=\frac{E|X-Y|}{2}=\frac{1}{\sqrt\pi}$
相关系数
协方差是有量纲的量,譬如X表示人的身高,单位是米(m) , Y表示人的体重,单位是千克(kg) .则Cov(X,Y) 带有量纲$(m\cdot kg)$
为了消除量纲的影响,现对协方差除以相同量纲的量,得到相关系数的概念
定义:
上式为X与Y的(线性)相关系数
现在我们知道二维正态分布$N(\mu_1,\mu_2,\sigma_1,\sigma_2,\rho)$ 的相关系数是 $\rho$
性质1
这个性质表明:相关系数介于 -1 和 1 之间。
性质2
$Corr(X,Y)=\pm 1$ 的充要条件是 X与Y 之间几乎处处有线性关系,即存在 a与b,使得 $P(Y=aX+b)=1$
其中当$Corr(X,Y)=1$时,有 $a>0$,称X与Y 完全正相关; $Corr(X,Y)=-1$ 时,有$a<0$,称X与Y 完全负相关
性质3
在二维正态分布 $N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$ , 不相关与独立是等价的
y因为二维正态分布$N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$ 的两个边际分布为 $N(\mu_1,\sigma_1^2)$和$N(\mu_2,\sigma_2^2)$ ,所以记其联合非密度为$p(x,y)$.边际密度函数为$p_X(x)$ 与 $p_Y(y)$
那么当 $\rho =0$ 时,可从正态密度函数的表达式中看出: $p(x,y)=p_X(x)p_Y(y)$ 即 $X$ 与 $Y$ 相互独立
反之,若X与Y相互独立,则X与Y 不相关,从而有 $\rho =0$
例题
已知随机向量$(X,Y)$的联合密度函数为:
$p(x,y)=\begin{cases}\frac{3}{8} ~~0<x-y<0.5,0<x,y<1 \ \ 0 ~~ 其他\end{cases}$
求 X,Y 的相关系数$Corr(X,Y)$
思路:
- 首先相关系数的公式 : $Corr(X,Y)= \frac{Cov(X,Y)}{\sigma_X\sigma_Y}=\frac{E(XY)-E(X)E(Y)}{\sigma_X\sigma_Y}$
- 先求边际密度函数,即 $pX(x)=\int{-\infty}^\infty p(x,y)dy$和$pY(y)=\int{-\infty}^{\infty}p(x,y)dx$
- 求 $E(X),E(Y),E(X^2),E(Y^2)$
- 求$Var(X),\sigma(X),Var(Y),\sigma(Y)$
- 带入求得
例题: 当相关系数结合多元函数
设随机变量X和Y独立同服从参数为$\lambda$ 的泊松分布,令:$U=2X+Y,V=2X-Y$ ,求U和V的相关系数 $Corr(U,V)$
如果按照常规方法,可以先求出 $p(u,v)$,然后求出 $p_U(u)、p_V(v)、E(U)、E(V)、Var(U)、Var(V)$ ,再求出$Corr(U,V)$ 但是这样太麻烦了。
我们可以通过方差的性质和协方差的性质来求解,因为我们已经知道了 $E(X),E(Y),Var(X),Var(Y)$ 根据泊松分布的可加性,我们可以进而求出 $E(U),E(V),Var(U),Var(V)$
因此,$Corr(U,V)=Cov(U,V)/\sqrt{Var(U)Var(V)}$
又:
因此 $Corr(U,V)=\frac{3\lambda}{5\lambda}=\frac{3}{5}$
随机向量的数学期望向量与协方差矩阵
记n维随机向量为 $X=(X_1,X_2,\cdots,X_n)’$ ,若其每个分量的数学期望都存在,则称:
为n为随机向量X的数学期望向量,简称为X的数学期望。
称
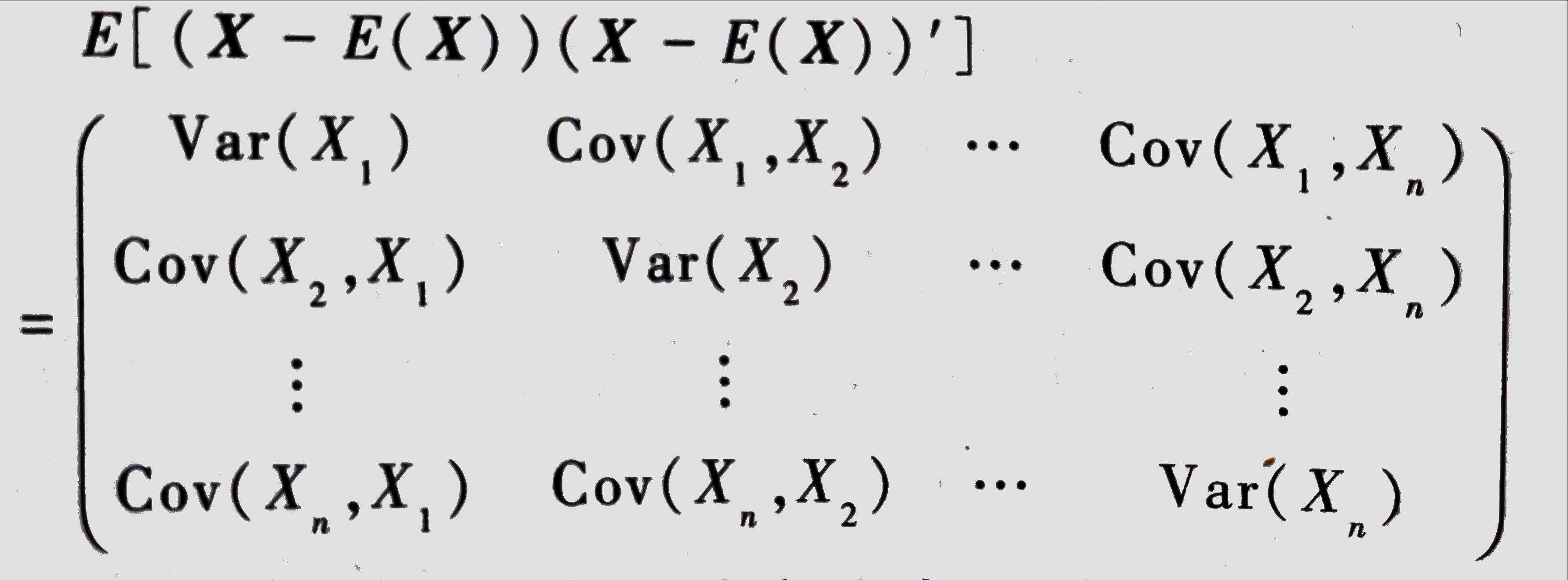
为该向量的方差-协方差 矩阵,记为$Cov(X)$
性质1
n为随机向量的协方差矩阵 $Cov(X)=(Cov(Xi,X_j)){n\times n}$ 是一个对称的非负定矩阵,也就是说其行列式值是大于等于0的。
条件分布与条件期望
条件分布
离散随机变量的条件分布
条件分布列
现在我们给出离散随机变量的条件分布列定义:
对于一切使 $P(Y=yi)=p{\cdot j}=\sum{i=1}^\infty p{ij}>0$ , 称
为给定$Y=y_j$ 条件下X的分布列
同理,一切使得 $P(X=xi)=p{i\cdot}=\sum{j=1}^\infty p{ij}>0$ 的$x_i$ ,称
为给定 $X=x_i$条件下 Y 的条件分布列
条件分布函数
有了条件分布列,我们就可以给出离散随机变量的条件分布函数
给定$Y=y_j$ 条件下 X的条件分布函数为:
给定$X=x_i$ 条件下 Y 的条件分布函数为:
例题1:求条件分布
设随机变量 X 与 Y互相独立,且 $X\sim P(\lambda_1),Y\sim P(\lambda_2)$ 。在已知道 $X+Y=n$ 的条件下,求 X 的条件分布。
第一步,求P(X+Y)的分布,(先求联合分布列)
一般来说如果X与Y独立同分布,那么我们就要利用多元随机变量函数的性质来求,表现在:二项分布、泊松分布、正态分布、伽马分布(卡方分布) 的可加性上。
首先我们要知道独立泊松变量的和仍然为泊松变量。即 $X+Y\sim P(\lambda_1+\lambda_2)$ ,
第二步,带入条件分布
消除指数之后,同分可得到:
这就是一个二项分布,说明,在 $X+Y=n$的条件下,X服从二项分布 $b(n,p)$,其中$p=\frac{\lambda_1}{\lambda_1+\lambda_2}$
例题2:
设在一段时间内进入某一商店的顾客人数X服从泊松分布$P(\lambda)$ ,每个顾客购买某种物品的概率为p,并且各个顾客是否购买该种物品相互独立,求进入商店的顾客购买这种物品的人数Y的分布列,以及$E(Y),Var(Y)$
首先我们列出X的分布列:$P(X=m)=\frac{\lambda^m}{m!}e^{-\lambda}, m=0,1,2\cdots$ . 那么m就是进入商店的人数。
同时,我们给出购买某种物品的人数Y的条件分布。很容易理解这是一个二项分布:
由全概率公式,可以得到:
显然,求和部分就像是 一个泊松分布的求和,其值为1
剩余的部分期望和方差都为 $\lambda p$, 标准差为 $\sqrt{\lambda p}$
这个例子可以告诉我们,在直接寻求Y的分布有困难时,有时借助条件分布可以把困难解决
例题3: 求条件分布列
试求条件分布列 $P(Y=m|X=n)$
第一步: 列出公式
第二步:根据公式,求出未知数
我们已经有了 $P(Y=m,X=n)$, 因此要求 $P_X(x)$ 这一个边际分布
我们看这里有 $m!(n-m)!$ 可以考虑将其配方成二项分布:
求和部分是一个二项分布列的求和,其值为1, 因此$P_X(x)=\frac{14^ne^{-14}}{n!}=P(14)$ 也就是说,X服从参数为14的泊松分布
第三步:带入求解
这是一个二项分布 $b(n,0.51)$
连续随机随机变量的条件分布
对一切使$P_Y(y)>0$ 的y,给定 $Y=y$ 条件下X的条件密度函数和条件分布函数分别为:
同理,对于一切使$p_X(x)>0$ 的x,给定$X=x$ 条件下Y的条件密度函数和条件分布函数分别为:
例题1: 求条件密度函数
设二维连续随机变量(X,Y) 的联合密度函数为:
试求条件密度函数$p(y|x)$
第一步: 列出条件密度函数公式
我们已经知道$p(x,y)$的联合密度函数,现在需要求 $p_X(x)$ 即x的边际密度函数
第二步:求p(x)
第三步:带入公式
$p(y|x)=\frac{3x}{3x^2}=\frac{1}{x}, 1<y<x$
例题2:求条件概率
求条件概率 $P(Y\geq 0.75|X=0.5)$
第一步:列出条件密度函数公式:
第二步,求p(x)
第三步,带入公式:
第四步,求条件边际分布
题目要求$P{Y\geq 0.75|X=0.5}$ ,因此,我们需要求 $P{y|x=0.5}$
第五步:求条件概率
连续场合的全概率公式和贝叶斯公式
1) 全概率公式的密度函数形式
2) 贝叶斯公式的密度函数形式:
条件数学期望
条件期望
条件分布的数学期望称为条件期望,其定义如下:
同理,
例题:求条件期望
设二维连续随机变量 $(X,Y)$ 的联合密度函数为:
试求 $E(X|Y=0.5)$
第一步:列出E(X|Y=y)的公式
发现 $p(X|Y=0.5)$这一个条件分布列是未知的。因此我们要求条件密度函数
第二步:求出条件密度函数
因为已知 $p(x,y)=x+y$, 现在就要求 $p_Y(y)$即y的边际分布
带入得到: $p(X=x|Y=y)=\frac{x+y}{y+\frac{1}{2}}$
所以 $p(X|Y=0.5)=x+0.5$
第三步,代入第一步公式求解
重期望公式
设 $(X,Y)$ 是二维随机变量,且 $E(X)$ 存在,则 $E(X)=E(E(X|Y))$
重期望公式的具体使用如下:
(1) 如果Y是一个离散随机变量,则上式可以写成
(2) 如果Y是一个连续随机变量,则上式可写成
例题:求二元函数的期望
设随机变量X与Y独立同步,都服从参数为 $\lambda$ 的指数分布,令
求$E(Z)$
第一步: 先分析思路
要求$E(Z)$,其中Z是一个二元函数,因此这道题可以从两种思路来求解:
第一种就是用二元函数期望公式来就算;
第二种就是用条件期望(重期望公式)来计算
第二步:用第一种方法——二元函数期望
首先我们求X,Y的联合分布 $p(x,y)$ : $X\sim \lambda e^{-\lambda x}, Y\sim \lambda e^{-\lambda y}$
$p(x,y)=p(x)p(y)=\lambda^2 e^{-\lambda x-\lambda y}$
我的思路是拿到题目首先考虑二元函数期望公式:
第三步:用第二种方法——条件期望
在 $X=x$ 给定时, $Z=\begin{cases}3X+1 ,X\geq Y\ \6Y,~~ X<Y \end{cases}$ 是关于Y的函数。注意,这里不要用 $E(Z|X)=\int{-\infty}^{\infty} zp(z|x)dz$ 来计算。而是说,把 $Z$ 看做是 $g(Y)$, 然后通过公式 $E(g(Y))=\int{-\infty}^\infty g(y)p_Y(y)dy$ 来计算。 同理,可以将其看成是$Y=y$ 条件下X的函数
根据重期望公式, $E(E(Z|X))=\int_{-\infty}^\infty E(Z|X)p_X(x)$求解:
$E(Z)=E(E(Z|X))=E[3X+1+e^{-\lambda X}(3X+\frac{6}{\lambda}-1)]$
很显然,使用重期望公式来做这道题非常的方便简洁
二维正态分布
$N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$ 的两个条件分布仍是正态分布,即
可见,在二维正态分布之中,一个变量的条件期望是另一个变量取值的线性函数,常称为一元线性回归方程。
随机个随机变量和的数学期望
设 $X_1,X_2\cdots$ 为一列独立同分布的随机变量,随机变量N只取正整数值,且$N$ 与 ${X_n}$ 独立,证明它们的和的期望
这里我引入一个N, 让 $N\sim p_N(n)$
利用重期望公式,可以把 $E(\sum_{i=1}^N X_i)$写成:
进而,在N=n 的情况下,上式可写为:
我们又知道,$Xi$和$N$是独立的,所以 $\sum{n=1}^n X_i $ 与N独立,所以条件期望可以转换成无条件期望
我们知道期望和有限个求和符号是可以交换的,我们把括号中的求和提出,变成n。原式可以写成以下形式:
将$E(X1)$提出,剩下的 $\sum{n=1}^\infty E(X_1)p_N(n)$可以写成是 $E(N)$
例题:
上面证明了和的期望,现在来证明和的方差。
证明
首先我们要知道一个公式: $Var(X)=E_Y(Var_X(X|Y))+Var_Y(E_X(X|Y))$
因此,原式 $Var(\sum_{i=1}^N(X_i))$ 可写为:
我们将其设为 $I_1+I_2$
先来化简 $I_1$ ,可以将其看成是N的函数,