假设检验

假设检验的基本思想与概念

我们先举一个女士品茶的例子：有一个女士称她可以鉴别奶茶是先加奶后加茶(MT)还是先加茶后加奶(MT). 那么，我们怎么来检验她是否有这种能力呢？

我们给出一个假设H：该女子没有这种鉴别能力。那么，如果H是正确的，她在10杯奶茶中只能猜，10次都猜对的概率为 $2^{-10}<0.001$ ，这是一个很小的概率，在一次试验中几乎不会发生，但如果这件事情真的发生的话，我们不能否决假设成立，但是更倾向于拒绝假设，从而认为该女士的确有辨别奶茶中 TM还是MT 的能力。

费舍尔用实验结果对假设H的对错进行判断的思维方式如下：

加入试验结果与假设H发生锚段就拒绝原假设H，否则就接收原假设

我们记女士判断正确的杯数为 X, $x_i\sim b(1,p)$ ，那么原假设H_0是无能力：$p=0.5$, 备择假设H_1有能力：$p>0.5,p\neq 1$

我们可以给出一张表：

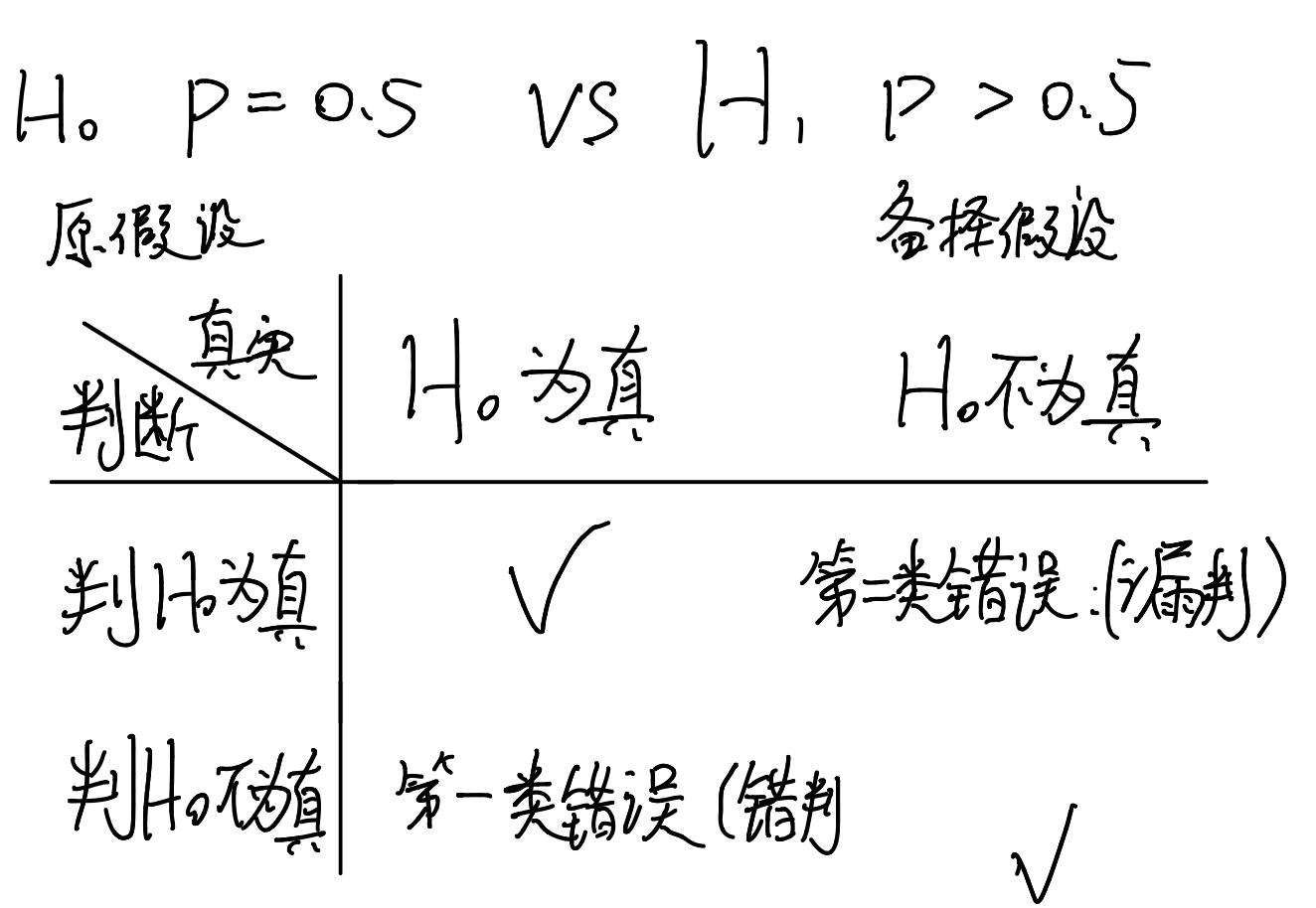
第一类错误的含义是：实际上她是没有这种能力的，但是呢，我们判定的结果是她有这种能力。也就是错判

第二类错误的含义是：实际上她是有这种能力的，但是我们却认为它没有这种能力。就像是漏掉了，也就是漏判。

在假设检验中，我们是无法让错判概率和漏判概率同时取很低的，因为它们两者是矛盾的，如下面这个例子

$x\sim N(\mu,\sigma_0^2)$, $\sigma_0^2$ 是已知的，$x_1,\cdots,x_n$ 是样本。

第一步是给出假设. 检验样本均值是否恰好等于$\mu_0$ 还是大于 $\mu_0$(一个已知量)

$H_0: \mu = \mu_0 ~~~vs~~~ H_1: \mu>\mu_0$

那么，如果我算出来的均值是$\overline x\geq c$的话，就很倾向于拒绝原假设。

那么怎么确定这个 c 值呢？我们先来看看错判概率$\alpha$
在 $H_0$ 成立的情况下，$\mu = \mu_0$, 此时 $\overline x\sim N(\mu_0,\sigma_0^2/n)$ , 那么我们判断其不为真的概率为：

$\alpha = P_u(\overline x>c)=P(\frac{\overline x-\mu_0}{\sqrt{\sigma_0^2/n}}>\frac{c-\mu_0}{\sqrt{\sigma_0^2/n}}) = 1-\Phi(\frac{c-\mu_0}{\sqrt{\sigma^2/n}})$

现在我们看看漏判概率
在 $H_1$ 成立的情况下，$\mu> \mu_0$ ，$\overline x\sim N(\mu,\sigma_0^2/n)$ .

在楼盘情况下，我判断$H_0$ 为真，则：

$\beta = P_\mu(\overline x< c) = P(\frac{\overline x-\mu }{\sqrt{\sigma_0^2/n}}<\frac{c-\mu }{\sqrt{\sigma_0^2/n}}) = \Phi(\frac{c-\mu }{\sqrt{\sigma^2/n}})$

要时刻记住，这时候的$\mu$ 是大于$\mu_0$ 的，不能用$\mu_0$ 带入

我希望$\alpha$ 越小，那么我们希望 c越大，而 c越大则必然导致 $\beta$ 越大。因此 $\alpha$和 $\beta$ 之间是冲突的。

说完了这个例子，我们可以顺理成章得给出显著性水平的定义：

对检验问题 $H_0:\theta\in\Theta_0 ~~~vs~~~ H_1\in \Theta_1$ ，如果一个检验满足对任意的$\theta\in \Theta_0$ 其犯第一类错误的概率$\leq \alpha$
则称该检验是显著性水平为$\alpha$的显著性检验，简称水平为$\alpha$的检验

提出显著性检验的概念就是要控制犯第一类错误的概率$\alpha$ ，不能让其过大与过小。在适当控制$\alpha$ 中制约$\beta$。最长使用的选择是 $\alpha=0.05$, 又是也会选择 $\alpha = 0.1$ 或者 $\alpha = 0.01$

那么，既然整个 $1-\Phi(\frac{c-\mu_0}{\sqrt{\sigma^2/n}})$ 要等于 $\alpha$ ，那么 $\Phi(\frac{c-\mu_0}{\sqrt{\sigma^2/n}})$ 就是要等于 $1-\alpha$ 。也就是说，我们可以反解出c值

$\frac{c-\mu_0}{\sqrt{\sigma^2/n}} = u_{1-\alpha}\\~\\ c = u_{1-\alpha}\cdot\sqrt{\sigma^2/n} ~+\mu_0$

解得c之后，我们发现，c把样本空间切割成了两部分。据此我们又引出了拒绝域 的概念

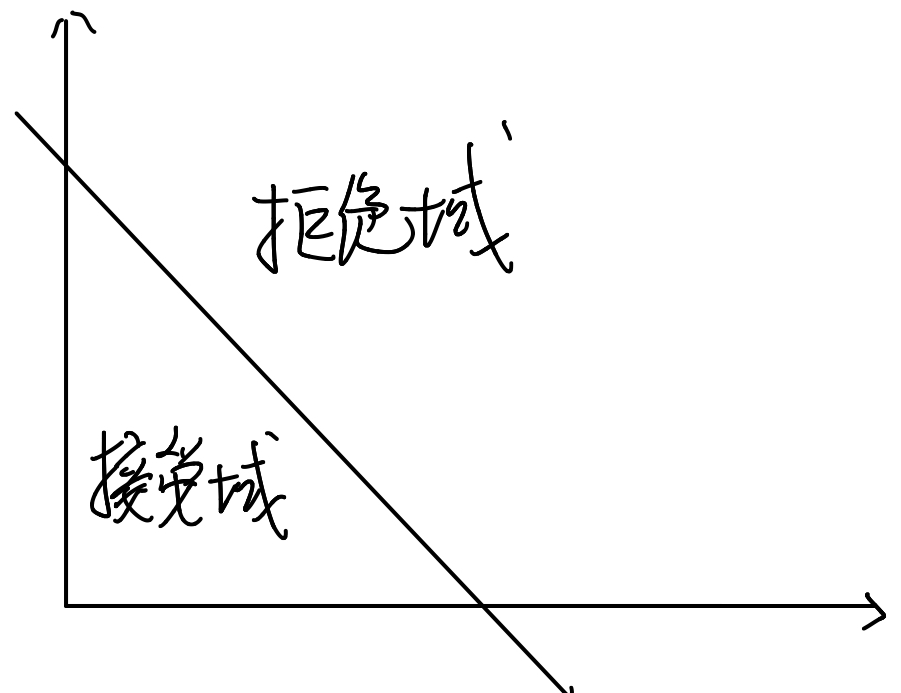
如果满足样本均值大于 $u_{1-\alpha}\cdot\sqrt{\sigma^2/n} ~+\mu_0$ 我们就拒绝原假设，这个域也被称为拒绝域
$W= \{(x_1,\cdots,x_n):\overline x>u_{1-\alpha}\cdot\sqrt{\sigma^2/n} ~+\mu_0\}$
而拒绝域的补集就是接受域

在一个二维平面中，拒绝域和接受域可表示如下：

现在再来一个例题：$x\sim N(\mu,\sigma^2)$, $\sigma^2$ 是未知的，$x_1,\cdots,x_n$ 是样本，同样是检验 $\mu$，计算拒绝域

第一步： 给出点估计，$\hat\mu = \overline x\sim N(\mu,\frac{\sigma^2}{n})$

第二步： 标准化：

$\frac{\overline x-\mu_0}{\sqrt{\sigma^2/n}}$

这时候由于$\sigma^2$ 未知，我们要用$s^2$ 去替代，替代完成后符合 t分布，即：

$t = \frac{\overline x-\mu_0}{\sqrt{s^2/n}} \sim t(n-1)$

第三步： 计算显著性水平

$\alpha = P(\frac{\overline x-\mu_0}{\sqrt{s^2/n}}>\frac{c-\mu_0}{\sqrt{s^2/n}})$

要把显著性水平用足，因此这里要等于$\alpha$ 不能 $p\geq \alpha$

我们知道$\frac{\overline x-\mu_0}{\sqrt{s^2/n}}\sim t(n-1)$ 说明

例4

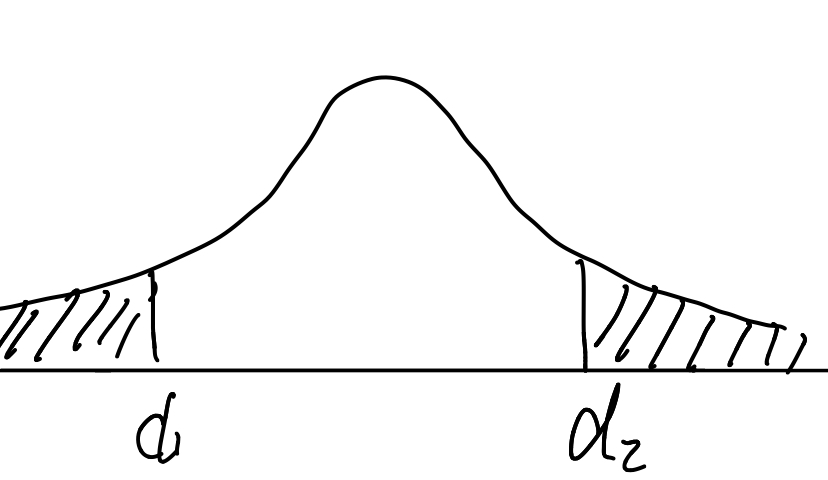
上面说的都是单边的假设检验问题，现在来看看双边假设。现在拒绝的标准就要变了。如下图所示,阴影部分都是需要拒绝的：

$\alpha = P(\frac{\overline x-\mu_0}{\sqrt{s^2/n}}\leq d_1)+P(\frac{\overline x-\mu_0}{\sqrt{s^2/n}}\geq d_2)$