吴恩达-机器学习1
一、 引言
监督学习
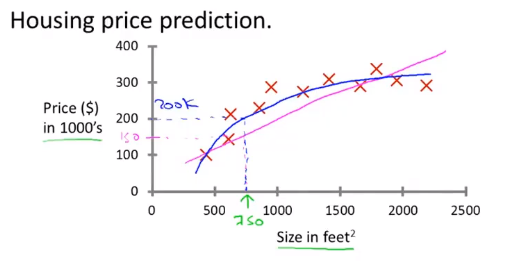
监督学习是指我们给计算机一个包含了正确数据(答案)的数据集,算法的目的就是给出更多的真确答案。这也被称为回归问题。比如说下面这张图,叉叉代表着搜集到的正确的数字。而我们要做的,是找出一条拟合的曲线,来预测某一个大小的房子的价格是多少。
虽然说价格最小精确到分,但是我们仍然可以将其认为是一个连续的值,因此可以用回归的模型来解决。回归的定义就是 : Predict continuous valued output.也就是预测连续的值。
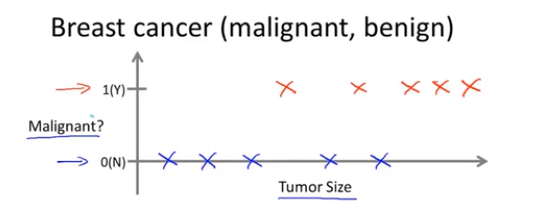
下面是另外一种监督学习的例子,横轴是肿瘤的大小,而数轴只有0和1,0代表良性肿瘤,1代表是恶性肿瘤。
或者是这样的一个有两个维度的分布:
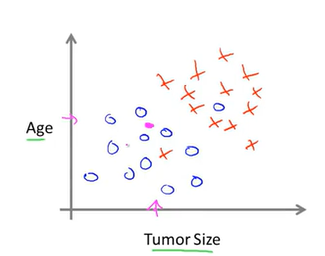
现在我们观测到一个肿瘤,我们的目的就是通过学习算法就将其归为某一类当中去。这是一个分类问题。比如第二张图,我们就可以在图上划出一条直线。
事实上,很多数据集不仅仅只有一个或者两个维度,可能有四五个或者更多特征。那怎么让学习算法能够处理这些特征呢?比如对于SVM(支持向量机),就有一个特别灵巧的数学方法(核函数),来允许计算机处理无穷多的特征
无监督学习
对于无监督学习,我们给出的数据是没有标签的,如下:
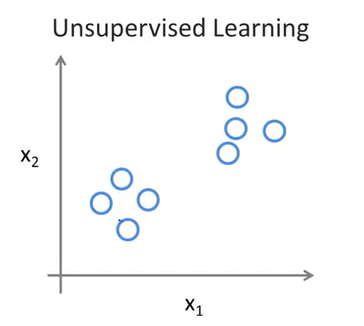
我们不知道每个数据点代表什么,我们只被告知这里有一个数据集,我们能不能在这里找到某种结构。通过无监督学习,我们可以在这个数据集中找到两个 clusters(簇) ,也就是说,这是我们之前学习过的聚类算法(K-Means)
无监督学习的一些实践:
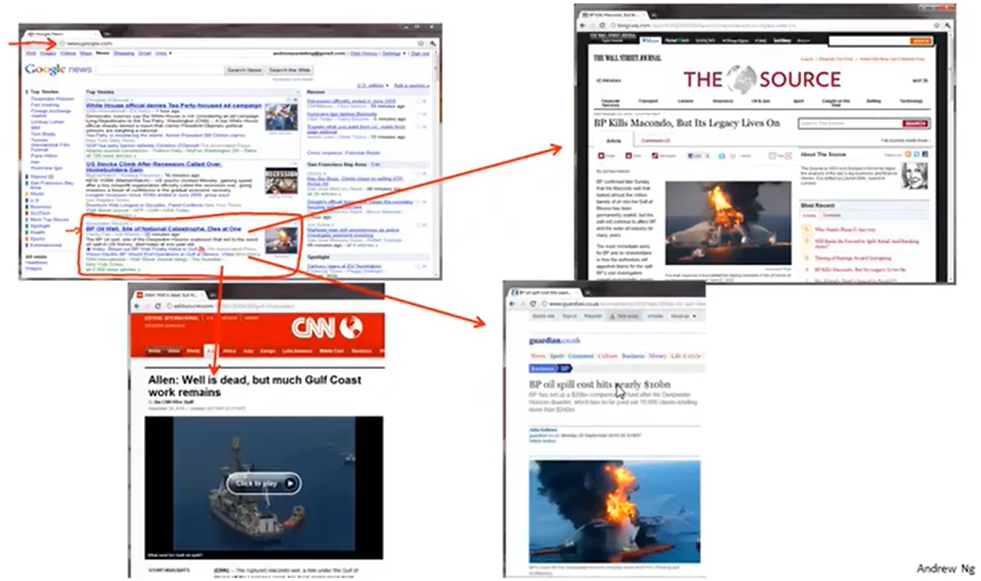
Google news:Google 每天会爬去数十万条新闻链接,然后将其聚类成一个一个新闻。比如说钻井平台新闻,集合了很多url,每个url指向不同新闻网站
聚类算法在基因组学中也有很多的应用。比如对于一个DNA微阵列数据的例子.
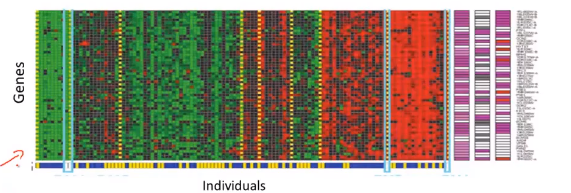
我们要做的就是运行一个聚类算法,把不同的个体归入不同的类或者归为不同类型的人。这是一种非监督学习,因为我们没有提前告知这个算法这些个体属于那一类人
非监督学习还可以用于社交圈,分析出和我们关系比较好的人,判断出哪些人互相认识并做推荐。在商业中,非监督学习可以将很多客户进行一个分类并进行精准的广告投放或者市场调研。
单变量线性回归
代价函数
了解代价函数有助于我们弄清楚如何把最有可能的直线与我们的数据拟合。比如说对于一个数据集,我们给出一个假设 $h_\theta (x)=\theta_0+\theta_1x$
$\theta_i’s $ 就是我们的参数。那么我们怎么才能选择 $\theta_0,\theta_1$ 来让拟合曲线更好地贴近我们的数据呢。我们用这样一个值来衡量 $\theta_0,\theta_1$ 是否合适。
其中,$h_\theta(x^{(i)})=\theta_0+\theta_1x^{(i)}$ 是观测值,而$y^{(i)}$ 代表实际值。
我们要试图找到 $\theta_0,\theta_1$ 来让上面这个式子的值最小。
由此我们可以引出代价函数的定义。代价函数的自变量就是$\theta_i$ ,也就是用来衡量我们选取的$\theta$ 是否合理,如下图所示:
代价函数也被称为平方误差函数。平方误差代价函数可能是解决回归问题最常用的手段了
代价函数的直观理解I
了解了原理之后我们来用例子说明代价函数是怎么操作的:
比如说现在我们的 $h\theta = \theta_1x$ 那么其代价函数就是 $J(\theta_1)=\frac{1}{2m}\sum{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$ ,我们要求的就是$\min J(\theta_1)$ 是的$\theta_1$
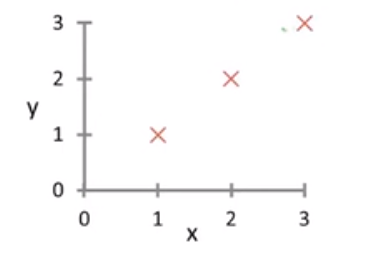
现在假设我们的训练集长这样,如果 $\theta_1=1$ 那么 $J(\theta_1)=0$ ; 如果 $\theta_1=0.5$, 那么 $J(\theta_1) = \frac{1}{2\cdot 3}[(0.5-1)^2+(1-2)^2+(1.5-3)^2] \approx 0.58$ 如果 $\theta_1=0$ 那么 $J(0) =\frac{1}{2 \cdot 3}(1^2+2^2+3^2) \approx 2.333 $
再取一些值、做了一些简单的比较之后,我们可以画出一个$J(\theta)$ 的图像,然后找到那个最小值,也就是 $\theta_1 = 1$ , 如下图所示:
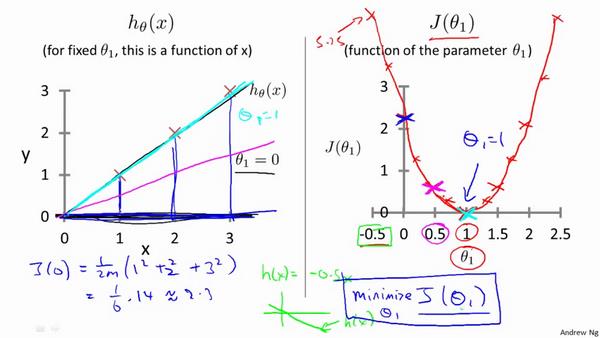
需要注意的是,$J(\theta)$ 是关于$\theta$ 的函数
代价函数的直观理解II
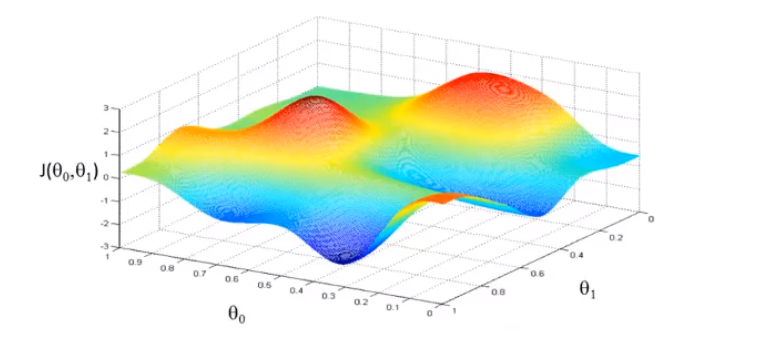
上面是一个 $\theta$ 值画出来的代价函数,长得像一个碗 ,那么如果是 2个 $\theta $ 值画出来的代价函数长什么样呢?这个和训练集有关,有可能长成这个样子:
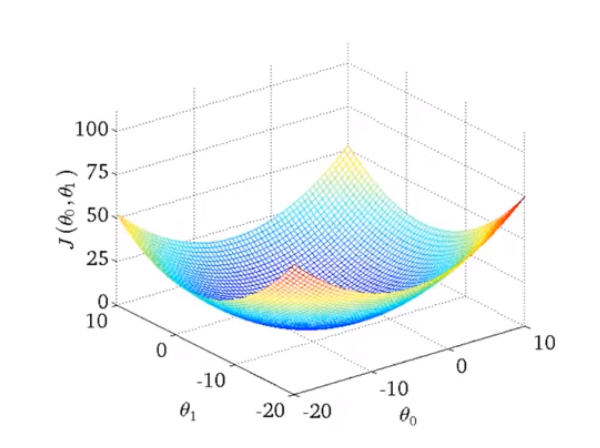
则可以看出在三维空间中存在一个使得$𝐽(\theta_0,\theta_1)$最小的点。
但是为了更好地展现三维图形,我们会使用等高线来表示含有两个参数的代价函数图像.如下图所示,在同一条等高线上,$J(\theta_0,\theta_1)$ 的取值都是一样的。我们要选择里中心点最近(也就是最低点)的$\theta_1,\theta_2$ 取值。
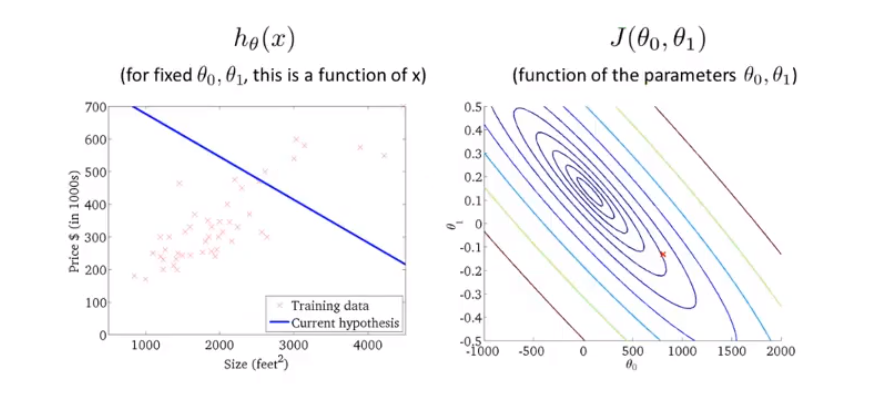
在接下来我们要学习一种可以自动找到这样满足 $\min J(\theta_0,\theta_1)$ 的 $\theta$ 的算法。也就是梯度下降算法
梯度下降
梯度下降算法能将函数 J 最小化,它不仅仅被用在线性回归上,还被广泛应用于机器学习的众多范畴。
梯度下降问题可以解决 很复杂的形如$J(\theta_0,\theta_1,\cdots,\theta_n)$ 的最小值,但这里方便起见只用 $J(\theta_0,\theta_1)$
算法的核心步骤其实很简单:
开始时我们随机选择一个参数的组合$(\theta_0,\theta_1,\cdots,\theta_n)$,计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
- 先给 $\theta_0,\theta_1$ 设置初始值(可以都为0)
- 一直改变 $\theta_0,\theta_1$ 的值,一直到我们找到 J 函数的最小值