单因子方差分析

Review:二样本独立t检验

首先我们复习一下二样本独立t检验，因为这时单因子方差分析的一种特殊情况。

目的： 比较两个方差相等的独立正态分布的均值是否相等。

数据：

$$\text{样本1:~~}x_{11},x_{12},\cdots,x_{1m_1}\\ \text{样本2:~~}x_{21},x_{22},\cdots,x_{2m_2}$$

假定$x_{ij}$是独立的随机变量，其分布为 $N(\mu_i,\sigma^2)$,那么

• $\mu_i$ 表示第 i 组的总体均值
• $\sigma^2$ 表示总体方差，是一个未知常数
• $i=1,2$
• $j=1,2\cdots,m$

我们的假设检验问题是：

$$H_0:\mu_1 = \mu_2 ~~vs~~ H_1:\mu_1\neq\mu_2$$

随后我们构造检验统计量t。检验统计量可以用枢轴量法导出来：

第一步： 求 $\theta$ 的点估计 $\hat\theta=\overline x-\overline y = \mu_1-\mu_2$

第二步： $\overline x\sim N(\mu_1,\frac{\sigma^2}{m}),\overline y \sim N(\mu_2,\frac{\sigma^2}{n})$​

$$\hat\theta = \overline x-\overline y \sim N(\mu_1-\mu_2,(\frac1m+\frac1n)\sigma^2)$$

第三步 标准化

$$\frac{\overline x-\overline y-\theta}{\sqrt{(\frac1m+\frac1n)\sigma^2}}\sim N(0,1)$$

显然这并不是一个枢轴量，因为存在位置变量$\sigma^2$ ,我们需要把 $\sigma^2$​ 换成样本方差。

第四步：

那么在两样本的时候由于样本量是不同的，样本方差就要用合方差来替换：

$$\hat\sigma^2 = s_w^2 = (\frac{1}{m_1+m_2-2})^{-1}((m_1-1)s_1^2+(m_2-1)s_2^2))$$

可以看做是$s_1^2$和$s_2^2$​​​的加权平均数。检验统计量可以写为：

$$\frac{\overline x-\overline y-\theta}{s_w\sqrt{(\frac1m+\frac1n)}}$$

又因为：

$$\frac{(m_1-1)s_x^2+(m_2-1)s_y^2}{\sigma^2}\sim\mathcal{X}^2(m_1+m_2-2)$$

所以当满足$H_0$ 成立时，

$$t = \frac{\overline x-\overline y}{s_w\sqrt{(\frac1{m_1}+\frac1{m_2})}}\sim t(m_1+m_2-2)$$

当$m_1=m_2=m$​ 时，检验统计量可简化为：检验统计量t服从自由度为$2(m-1)$

$$t = \frac{\overline x-\overline y}{\sqrt{\frac{1}{m}(s_1^2+s_2^2)}}\sim t(m_1+m_2-2)$$

拒绝域法

我们令：

$$W = \{|t|\geq t_{1-\alpha/2}(2(m-1))\}$$

$t_\alpha(2(m-1))$ 为自由度为$2(m-1)$的t分布的$\alpha$分位数

如果落在拒绝域，那么拒绝原假设，接收备择假设。$\mu_1\neq \mu_2$

如果未落在拒绝域，那么接受原假设，$\mu_1=\mu_2$​

p值法

$$p = 2P(t>|t_0|)$$

t表示自由度为$2(m-1)$ 的t分布的随机变量，$t_0$​ 是通过样本计算的检验统计量。

例子

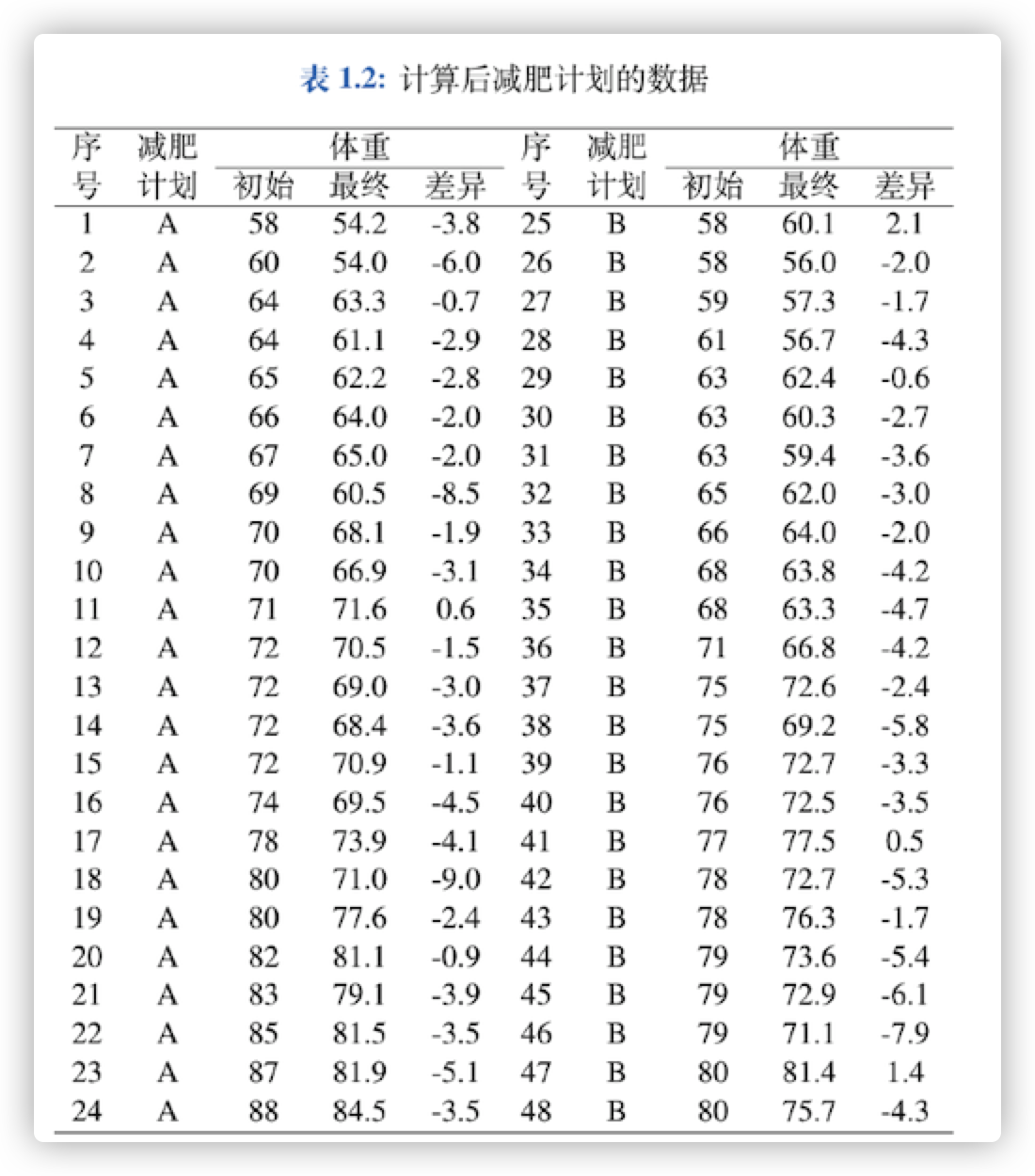
这里是一张减肥前后的差异变化表。我们令$x{1j}$ 为减肥计划A六周前后的体重差异，$x{2j}$​ 表示减肥计划B六周前后的体重差异，$j=1,\cdots,24$

我们假设在$x_{ij}$独立的情况下：

$$x_{ij}\sim N(\mu_i,\sigma^2) ,~~i = 1,2,j=1,2,\cdots,24$$

那么我们给出假设检验：

$$H_0 : \mu_1 = \mu_2~~~ vs ~~~H_1:\mu_1\neq \mu_2$$

同时计算得到：

$$\overline x_1 = -3.3 ,s_1^2 = 5.0183 \\~\\ \overline x_2 = -3.1125,s_2^2 = 5.7072\\~\\ s_w^2 = 5.3627$$

检验统计量为：

$$t = \frac{\overline x_1-\overline x_2}{s_w\sqrt{2/m}} = -0.2805$$

取显著性水平 $\alpha = 0.05$，则拒绝域为：

$$\{|t|\geq t_{1-\alpha/2}(2m-2)\} = \{|t|\geq 2.0129\}$$

我们发现计算得到的t并为落在拒绝域，因此我们接收原假设，两种减肥计划的效果是一致的

单因子方差分析的模型及假设

基本定义

那么问题来了，如果现在有三种减肥方式，我们又该怎么处理呢？两两做一次二样本独立t检验吗？显然这样比较耗费时间。因此我们提出了单因子方差分析模型

响应变量：我们关心的随机变量，一般用 y 来表示

因子：引发响应变量y大小变化的因素，一般用大写字母表示，例如：A，有a种不同的取值，通常 $a\geq 2$; 称因子A的一种取值为一个水平或者一个处理。

重复次数：在因子A每个水平下，随机变量的个数，记为m

在减肥方案的比较这个例子中：

• 减肥计划前后的体重差作为响应变量
• 减肥计划为所关心的因子，$a=2$
• 每组有24名志愿者，即 $m=24$
• 样本量： $n = a\cdot m = 48$​

现在，我们来定义一下这个模型中要用到的数据结构：

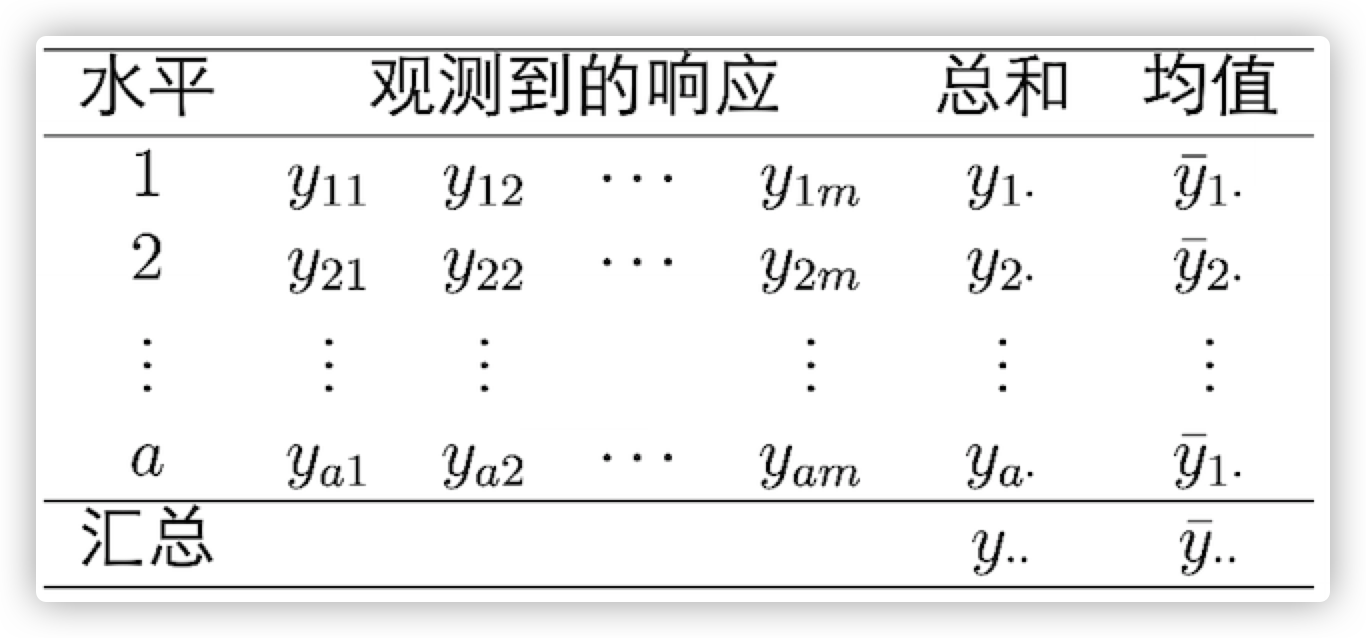
其中：

• $y_{ij}$ 表示在第i个水平下观测到的第j个响应变量
• $y_{i\cdot}$ 表示在第i个水平下响应变量的总和
• $\overline y_{i\cdot}$ 表示在第i个水平下响应变量的均值
• $y_{\cdot\cdot}$ 表示所有响应变量的总和
• $\overline y_{\cdot\cdot}$ 表示所有响应变量的均值

也就是说我们可以列出如下关系：

$$\begin{align} &y_{i\cdot} = \sum_{j=1}^m y_{ij}\\ &\overline y_{i\cdot} = \frac{y_{i\cdot}}{m} ~~i = 1,2\cdots,a\\~\\ &y_{\cdot\cdot} = \sum^a_{i=1}\sum_{j=1}^m y_{ij} \\ &\overline y_{\cdot\cdot} = \frac{y_{\cdot\cdot}}{n} \end{align}$$

均值模型

现在我们来定义两种模型：均值模型和效应模型

均值模型如下：

首先给出假设，

$$H_0 : \mu_1 = \mu_2 = \cdots = \mu_a\\~\\ H_1 : \text{存在 在两种水平i,j下的均值不相等，即}\mu_i\neq\mu_j$$

给出模型定义：

$$y_{ij} = \mu_i+\varepsilon_{ij}, \begin{cases} i=1,2\cdots,a \\ j=1,2\cdots,m \end{cases}$$

其中，

• $\mu_i$ 表示因子的第i个水平下的均值
• $\varepsilon{ij}$ 是随机误差，通常认为随机误差的期望为零，即 $E(\varepsilon {ij})=0$​ 。因为如果 $E(y_{ij})$ 不为0，那么这个期望我们是看不到的，在估计的时候就会有两个期望，我们没有办法分开 $E(y)$和$E(\varepsilon)$ ，导致识别不了参数。

我们可以明显的看出：$E(y_{ij}) = \mu_i,j=1,2\cdots,m$​

这个模型就被称为均值模型，因为这个模型只和均值有关系

效应模型

除了均值模型之外，方差分析里面还有一个模型叫做效应模型。

在因子的第i个水平下的均值可以划分成两部分：

• 其一为总体均值 $\mu = \frac{1}{a}\sum_{i=1}^a \mu_i$​
• 其二维第i个水平效应$\alpha_i$，也就是说，各个水平的效应是各个水平的均值与总体均值的偏差。

$$\mu_i = \mu+\alpha_i,~i = 1,2\cdots,a$$

也就是有一个和组别没有关系的值加上一个和组别有关系的效应值。

然后可以写出效应模型的形式：

$$y_{ij} = \mu+\alpha_i+\varepsilon_{ij}, \begin{cases} i=1,2\cdots,a \\ j=1,2\cdots,m \end{cases}$$

相对于均值模型，效应模型参数个数有所增加。但是这样会存在一种状况，$\alpha$ 取不同的几组值可能会得到相同的结果。因此为了避免参数无法识别的问题，我们通常需要对参数给出一个合理的约束。最常见的为：

$$\sum_{i=1}^n \alpha_i = 0$$

这表明了，因子A的各个水平的效应在零的附近波动，且所有的效应总和为0

此外，还有一种条件是： $\alpha1=0$, 这个方程会导致参数的含义发生了变化。使用$\sum{i=1}^n \alpha_i = 0$​，$\alpha$表示效应；而$\alpha_1 = 0$​​ /**TODO:思考此时参数是什么含义**/.

现在给出效应模型的假设，

$$H_0 : \alpha_1 = \alpha_2 = \cdots = \alpha_a\\~\\ H_1 : \text{存在第i个水平不为0，即} \alpha_i\neq 0$$

在效应模型中：

$$\mu_i = \mu+\alpha_i,i=1,2\cdots,a$$

总之，无论是均值模型还是效应模型，都仅考虑了一个因子，所以，称这两个模型为单因子方差分析模型

误差假定

现在我们来假定随机误差：独立同分布条件下，随机误差是以均值为0，方差为$\sigma^2$的正态分布的随机变量

$$\varepsilon \sim N(0,\sigma^2)$$

这表明：在不同水平下，响应变量的波动大小是一致的；观测到的数据是相互独立且均服从正态分布，即：

$$y_{ij}\sim N(\mu+\alpha_i,\sigma^2)$$

注意！： 观测到的数据是相互独立的，但并不是同分布的，因为每组的均值可能是不相等的。

总结

单因子方差的模型为：

$$y_{ij} = \mu+\alpha_i+\varepsilon_{ij},\varepsilon_{ij}\sim N(0,\sigma^2),\begin{cases} i=1,2\cdots,a \\ j=1,2\cdots,m \end{cases}\\~\\ \text{s.t. } \sum_{i=1}^a \alpha_i = 0$$

现在我们可以用单因子方差分析去写一个二样本t检验的模型，如下：

$$y_{ij} = \mu+\alpha_i+\varepsilon_{ij},\varepsilon_{ij}\sim N(0,\sigma^2),\begin{cases} i=1,2 \\ j=1,2,\cdots,m \end{cases}\\~\\ \text{s.t. } \sum_{i=1}^2 \alpha_i = 0$$

单因子方差分析的检验

我们再回到二样本t检验，我们在检验两组均值是否相等的本质就是比较两组样本均值差异与数据波动的大小。

所以，相比与数据的波动，两组样本均值的差异要大得多，那么我们才有足够的证据支撑说明这两组数据的均值是不一致的。

用一张图可以很清楚的解释：

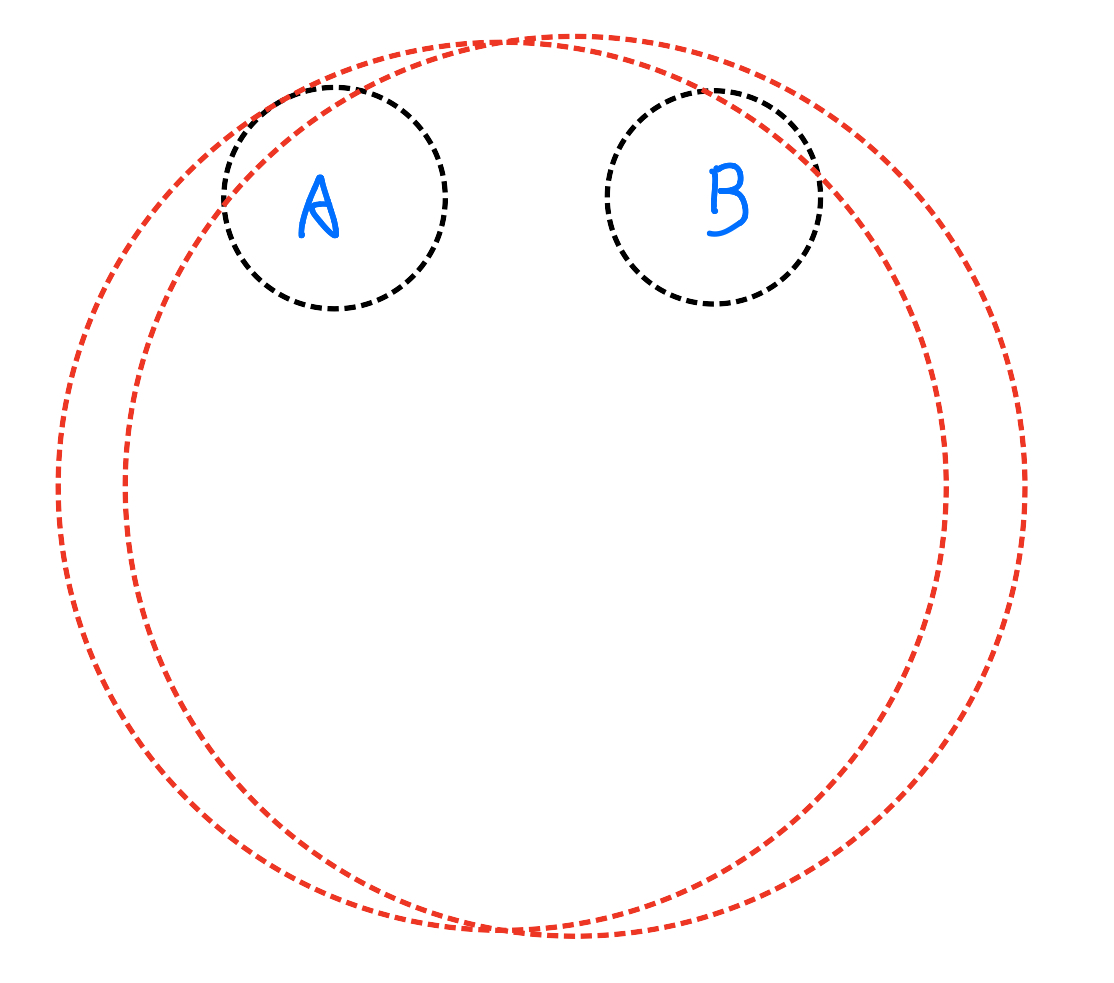
A和B是两组样本，如果取自两个黑圈，那么显然两组样本的均值是不相等的。但是如果取自两个红圈，那么相比于数据的波动，两组样本均值差异不明显，因此可以认为两组均值相等。

偏差平方和

那么当$a\geq3$时，我们又该怎么分析呢？如下图：

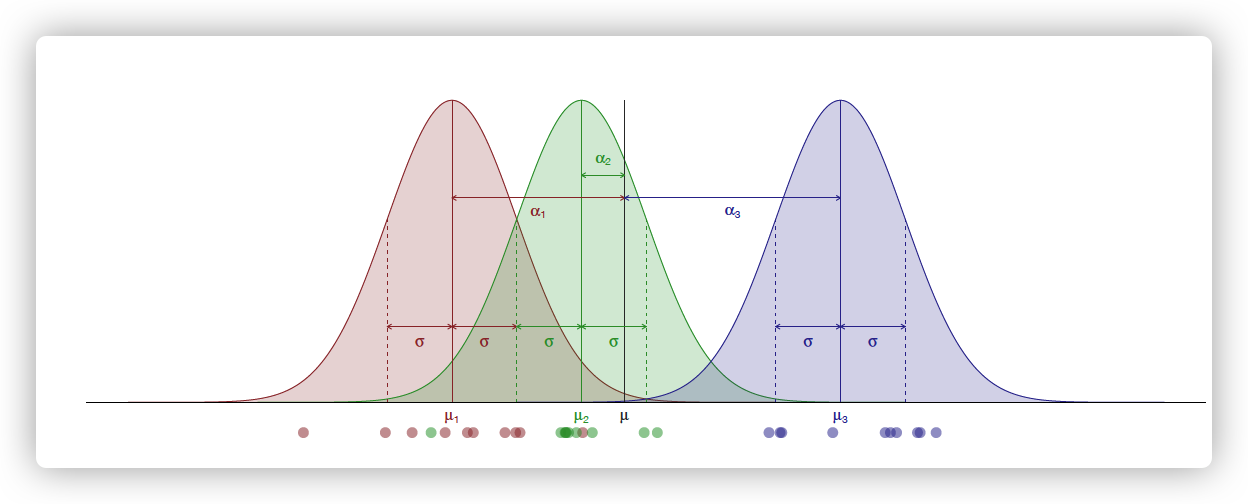
观测这张图，我们发现，不同组别的均值是和对应的效应值$\alpha_i$相关的。此外，我们将所有数据看成一个整体，那么这个整体的波动又是和整体的方差有关的。

为了分清楚这两者，我们需要推导一下偏差平方和的分解公式。

总偏差平方和等于所有点到所有响应变量的均值的偏差平方和

$$SS_T = \sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\overline y_{..})^2$$

$SS_T$​ 可以拆分成两部分，也就是在里面加一项减一项，这是概率论的常见技巧。

$$\sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\overline y_{..})^2 = \sum_{i=1}^a\sum_{j=1}^m((\overline y_{i\cdot}-\overline y_{\cdot\cdot})+(y_{ij}-\overline y_{i\cdot}))^2\\~\\$$

然后，第一部分是和j没有关系的，因此可以写为：

$$= m\sum_{i=1}^a(\overline y_{i\cdot}-\overline y_{\cdot\cdot})^2+\sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\overline y_{i\cdot})^2+2\sum_{i=1}^a\sum_{j=1}^m(\overline y_{i\cdot}-\overline y_{\cdot\cdot})(y_{ij}-\overline y_{i\cdot})$$

再来，我们要敏锐的发现，交叉项是0，这是因为：

$$2\sum_{i=1}^a\sum_{j=1}^m(\overline y_{i\cdot}-\overline y_{\cdot\cdot})(y_{ij}-\overline y_{i\cdot}) = 2\sum_i(\overline y_{i\cdot}-\overline y_{\cdot\cdot})\sum_{j}^m(y_{ij}-\overline y_{i\cdot})\\~\\ \sum_{j}^m(y_{ij}-\overline y_{i\cdot}) = y_{i\cdot}-m\overline y_{i\cdot} = y_{i\cdot}-y_{i\cdot} = 0$$

因此，平方和分解公式的最终结果如下：

$$\sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\overline y_{..})^2 = m\sum_{i=1}^a(\overline y_{i\cdot}-\overline y_{\cdot\cdot})^2+\sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\overline y_{i\cdot})^2$$

$SS_A$

其中，第一项为组间偏差平方和$SS_A$ ,即

$$SS_A = m\sum_{i=1}^a(\overline y_{i\cdot}-\overline y_{\cdot\cdot})^2$$

$SS_A$ 表示了不同水平下，数据的平均值与所有数据的总平均值之间的偏差平方和，既包含了因子A取不同水平引起的数据差异，又包含了随机误差对其的影响。

$SS_E$

第二项为组内偏差平方和 $SS_E$, 即：

$$SS_E =\sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\overline y_{i\cdot})^2$$

$SSE$ 表示同一水平下数据$y{ij}$与其平均值 $\overline y_{i\cdot}$的差异，是实验误差引起的

检验统计量

平方和分解公式可以简记为：

$$SS_T = SS_A+SS_E$$

对于给定的一组数据，总偏差平方和$SST$ 是不变的。如果原假设成立，$SS_A$仅仅收到随机误差方差的影响，取值应该不大。是因为每组的样本均值 $\overline y{i\cdot}$ 是$\mu_i$的一个合理的估计。

因此一个直观的想法是比较$SS_A/SS_T$ 。如果这个比值越大，说明$SS_A$ 不仅仅受到误差的影响，因此我们越有证据支持备择假设；反之，我们认为原假设更合理

但是在单因子反差分析模型中，我们所构造的检验统计量是基于： $SS_A/SS_E$ 的。其实将$SS_E$ 带换掉，我们发现$SS_A/SS_E$是随着 $SS_A/SS_T$的增大而增大的。

定理1

在单因子方差分析模型中，有：

• 组内偏差平方和$SS_E$ 的分布为：

$$\frac{SS_E}{\sigma^2} \sim \mathcal{X}^2(n-a)$$

证明

根据单因子方差分析模型： $y{ij} = \mu+\alpha_i+\varepsilon{ij}$​​ ，将其带入$SS_E$公式可得

$$SS_E = \sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\overline y_{i\cdot})^2 \\ =\sum_{i=1}^a\sum_{j=1}^m ((\mu+\alpha_i+\varepsilon_{ij})-\frac{1}{m}\sum_{j=1}^m(\mu+\alpha+\varepsilon_{ij}))^2$$

我们将求和符号打散，发现前两项可以保持不变(m消掉)，最后一项变为 $\frac{1}{m}\sum{j=1}^m\varepsilon{ij}$​ ，也就是每组的误差均值

$$SS_E=\sum_{i=1}^a\sum_{j=1}^m ((\mu+\alpha_i+\varepsilon_{ij})-\mu-\alpha-\frac{1}{m}\sum_{j=1}^m\varepsilon_{ij})^2\\~\\ =\sum_{i=1}^a\sum_{j=1}^m(\varepsilon_{ij}-\overline \varepsilon_{i\cdot})^2$$

同时，我们要知道 $\varepsilon_{ij}$是独立同分布的正态随机变量，即：

$$\varepsilon_{ij} \sim N(0,\sigma^2)$$

那么，在因子 A 的第i个水平下，$\varepsilon{i1},\cdots,\varepsilon{im}$ 可以看做来自正态总体 $N(0,\sigma^2)$的一组样本量为m的样本，而$\overline\varepsilon{i\cdot} = m^{-1}\sum{j=1}^m\varepsilon_{ij}$​可以看做是这组样本的样本均值。那么构造卡方就呼之欲出了。

$$\frac{SS_E}{\sigma^2}=\sum_{i=1}^a[\frac{1}{\sigma^2}\sum_{j=1}^m(\varepsilon_{ij}-\overline \varepsilon_{i\cdot})^2],i=1,2\cdots,a\\~\\ \text{其中:}\frac{1}{\sigma^2}\sum_{j=1}^m(\varepsilon_{ij}-\overline \varepsilon_{i\cdot})^2\sim\mathcal{X}^2(m-1)$$

又由于不同水平下的偏差平方和是相互独立的，因此根据卡方分布的可加性，有：

$$\frac{SS_E}{\sigma^2} \sim \mathcal{X}^2(a(m-1))\\~\\ \text{注意到：~~} a(m-1) = am-a = n-a$$

定理2

在单因子方差分析模型中，有：

• 组间偏差平方和的期望为:

$$E(SS_A) = (a-1)\sigma^2+m\sum_{i=1}^a\alpha_i^2$$

特别的，在原假设 $H_0$成立时，有：

$$\frac{SS_A}{\sigma^2} \sim \mathcal{X}^2(a-1)$$

证明

证明策略与定理1类似，也是将$y{ij} = \mu+\alpha_i+\varepsilon{ij}$​ 代入

$$\begin{align} SS_A &= m\sum_{i=1}^a(\overline y_{i\cdot}-\overline y_{\cdot\cdot})^2\\ &=m\sum_{i=1}^a (\frac{1}{m}\sum_{j=1}^m(\mu+\alpha_i+\varepsilon_{ij})-\frac{1}{n}\sum_{i=1}^a\sum_{j=1}^m(\mu+\alpha_i+\epsilon_{ij}))^2\\ &= m\sum_{i=1}^a (\alpha_i+\overline \varepsilon_{i\cdot}-\overline\varepsilon_{\cdot\cdot})^2 \end{align}$$

到这一步都很顺利。 现在我们看到括号里面有 $\alpha_i$ 和$\varepsilon$ ，这两个参数分别是确定的和随机的，我们要做的就是拆分他们。

$$=m\sum_{i=1}^a\alpha_i^2+m\sum_{i=1}^a(\overline\varepsilon_{i\cdot}-\overline\varepsilon_{\cdot\cdot})+2m\sum_{i=1}^a\alpha_i(\overline\varepsilon_{i\cdot}-\overline \varepsilon_{\cdot\cdot})$$

对于交叉项，这是一个数我们没办法再化成0了，但是我们可以求交叉项的期望。

因为 $\varepsilon_{ij}\sim N(0,\sigma^2)$ 且相互独立，所以：

$$\overline\varepsilon_{i\cdot} = \frac{1}{m}\sum_{j=1}^m\varepsilon_{ij}\sim N(0,\frac{\sigma^2}{m})\\ \overline \varepsilon_{\cdot\cdot} = \frac{1}{n}\sum_{i=1}^a\sum_{j=1}^m\varepsilon_{ij}\sim N(0,\frac{\sigma^2}{n})$$

因此：

$$E(2m\sum_{i=1}^a\alpha_i(\overline\varepsilon_{i\cdot}-\overline \varepsilon_{\cdot\cdot})) = 2m\sum_{i=1}^a\alpha_iE(\overline\varepsilon_{i\cdot}-\overline \varepsilon_{\cdot\cdot})=0$$

但这样一来就需要对整个$SS_A$​求期望。

$$E(SS_A) = m \sum_{i=1}^a\alpha_i^2+mE(\sum_{i=1}^a(\overline\varepsilon_{i\cdot}-\overline \varepsilon_{\cdot\cdot})^2)$$

现在我们又要来凑卡方了

• 首先，$\overline \varepsilon{i\cdot}$ 是第i个水平下随机误差的样本均值，因为不同水平下的随机误差是相互独立的，所以，这些随机误差的样本均值 $\overline\varepsilon{1\cdot},\overline\varepsilon{2\cdot},\cdots,\overline\varepsilon{a\cdot}$是相互独立的。
• 又因为

$$\overline\varepsilon_{\cdot\cdot} = \frac{1}{n}\sum_{i=1}^a\sum_{j=1}^m\varepsilon_{ij}=\frac{1}{a}\sum_{i=1}^a\overline\varepsilon_{i\cdot}$$

可以看成是 a个$\overline\varepsilon{1\cdot},\overline\varepsilon{2\cdot},\cdots,\overline\varepsilon_{a\cdot}$ 的样本均值，因此卡方分布就呼之欲出了。

$$m(\sum_{i=1}^a(\overline\varepsilon_{i\cdot}-\overline \varepsilon_{\cdot\cdot})^2)/\sigma^2 \sim\mathcal{X}^2(a-1)\\ \sigma^2 E(m(\sum_{i=1}^a(\overline\varepsilon_{i\cdot}-\overline\varepsilon_{\cdot\cdot})^2)/\sigma^2 ) = \sigma^2(a-1)$$

综上，原式可以化简为：

$$E(SS_A) = m\sum_{i=1}^a\alpha_i^2+(a-1)\sigma^2$$

那么，当原假设 $H_0$成立时，因为 $\alpha_1=\alpha_2\cdots=\alpha_a =0$,我们有：

$$SS_A =m\sum_{i=1}^a(\overline\varepsilon_{i\cdot}-\overline \varepsilon_{\cdot\cdot})^2\\ SS_A/\sigma^2 =m\sum_{i=1}^a(\overline\varepsilon_{i\cdot}-\overline \varepsilon_{\cdot\cdot})^2/\sigma^2\sim\mathcal{X}^2(a-1)$$

定理3

在单因子方差分析模型中，有：

• 组间偏差平方和与组内偏差平方和独立。即

$$SS_A \bot~ SS_E$$

这是因为，

$$SS_A = m\sum_{i=1}^a(\alpha_i+\overline\varepsilon_{i\cdot}-\overline\varepsilon_{i\cdot})^2$$

这是关于$\overline\varepsilon{1\cdot},\overline\varepsilon{2\cdot},\cdots,\overline\varepsilon_{a\cdot}$ 的函数。

同时，我们也要知道 $\sum{j=1}^m(\varepsilon{ij}-\overline\varepsilon{i\cdot})^2$ 与 $\overline\varepsilon{i\cdot}$是相互独立的，而且因子不同水平下的随机误差是相互独立的。

所以，$SS_A$ 和 $SS_E$ 独立

由于$SS_E$​和$SS_A$ 都可以化成卡方分布的形式，那么我们就可以这样来确定检验统计量

$$F_A = \frac{SS_A}{a-1}/\frac{SS_E}{n-a}$$

在原假设 $H_0$成立下服从自由度分别为$a-1$和n-a 的F分布，即 $F_A\sim F(a-1,n-a)$

拒绝域法

在显著性水平 $\alpha$下，如果：

$$F_A\geq F_{1-\alpha}(a-1,n-a)$$

那么，我们会拒绝原假设。

p值法

计算p值来进行判断，即

$$p_A = P(F\geq F_A)$$

其中，$F_A$是通过样本计算而得的检验统计量，F为一个自由度为$a-1$和$n-a$的卡方分布的随机变量。如果 $p_A\leq \alpha$ 那么，我们会 拒绝原假设，否则我们无法拒绝原假设

单因子方差分析的参数估计

点估计

由于

$$y_{ij}\sim N(\mu+\alpha_i,\sigma^2)~~i=1,2\cdots,a ,j=1,2\cdots,m$$

我们可以用极大似然估计来估计参数

$$(\mu,\alpha_1,\alpha_2,\cdots,\alpha_a,\sigma^2)$$

似然估计为：

$$L(\mu,\alpha_1,\alpha_2\cdots,\alpha_a,\sigma^2) = \prod_{i=1}^a\prod_{j=1}\bigg\{\frac{1}{\sqrt{2\pi\sigma^2}}\exp\big\{-\frac{(y_{ij}-\mu-\alpha_i)^2}{2\sigma^2}\big\}\bigg\}$$

其对数似然函数为：

$$l(\mu,\alpha_1,\alpha_2\cdots,\alpha_a,\sigma^2) = \ln L(\mu,\alpha_1,\alpha_2\cdots,\alpha_a,\sigma^2)\\ =-\frac{n}{2}\ln(2\pi\sigma^2)-\sum_{i=1}^a\sum_{j=1}^m\frac{(y_{ij}-\mu-\alpha_i)^2}{2\sigma^2}$$

接下来对各个参数求偏导，得到似然方程为：

$$\begin{cases} \frac{\partial l}{\partial \mu}=\frac{1}{\sigma^2}\sum_{i=1}^a\sum_{i=1}^m(y_{ij}-\mu-\alpha_i)=0 \\~\\\frac{\partial l}{\partial\alpha_i} =\frac{1}{\sigma^2}\sum_{j=1}^m(y_{ij}-\mu-\alpha_i)=0 ~~i=1,2\cdots,a \\~\\ \frac{\partial l}{\partial\sigma^2} = -\frac{n}{2\sigma^2}+\frac{1}{2\sigma^4}\sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\mu-\alpha_i)^2 = 0 \end{cases}$$

其中，第一个方程式多余的，因为第二行中，a个方程组相加以后，就等于第一个方程式。因此我们还需要加上一个条件才能解出来，这个条件就是 $\sum_{i=1}^a\alpha_i=0$

于是，我们可以求出各个参数的极大似然估计为：

$$\begin{cases} \hat\mu=\overline y_{\cdot\cdot} \\~\\ \hat\alpha_i = \overline y_{i\cdot}-\overline y_{\cdot\cdot},i=1,2\cdots,a \\~\\ \hat\sigma^2_{MLE} = \frac{1}{n} \sum_{i=1}^a\sum_{j=1}^m(y_{ij}-\overline y_{i\cdot})^2 = \frac{SS_E}{n} \end{cases}$$

由极大似然估计的不变性，各个水平的均值$\mu_i$的极大似然估计为：

$$\hat\mu_i =\overline y_{i\cdot}$$

因为 $E(SSE)=\sigma^2(n-a)$ ，所以 $\hat\sigma^2{MLE}$ 并不是$\sigma^2$的一个无偏估计。

区间估计