软件优化-宾利法则

Posted on
Words count in article: 4.8k | Reading time ≈ 20

软件优化-宾利法则

现在我们来讲宾利法则，这个宾利不是车企，而是一个计算机学家。他提出了软件优化的若干法则。主要分为四个部分：数据结构，循环，逻辑，函数。每个部分又分为若干小点，现在我们来一一讲解

Data structures

Packing and encoding 压缩和编码

压缩的概念是用相同的机器语言表示尽可能多的数据，编码优化则是用尽可能少的bits去表示数据的值。

比如说，字符串”September 11,2018“ 能以18 bytes的大小被存储，这需要两个double(64-bits) words 才能放下。 这对于日期信息来说，是比较庞大的一段空间了。其实，要是计算公元前后4096年的日期，大概只要

就可以了，只需要 single word(32-bit) 就可以存储了

但是，修改了编码方式，并不意味着可以提升程序的性能。因为虽然空间上减少了很多。但是要计算得到这个编码，需要消耗更多的CPU性能，所以在这个情况下修改编码并不是一个很好地选择。

我们另辟蹊径，用另外一种数据结构来存储这些信息：

1
2
3
4
5
typedef struct {
	int year: 13;
	int month: 4;
	int day: 5;
} date_t;

用struct来存储这些信息，同样只要消耗22 bits(存储年份需要13位，一位表示公园前后)，但是计算速度要比上面那种编码快很多。

Augmentation 扩充策略

有些时候，我们对一个普通的数据结构加上一些信息，来让数据结构做更少的计算。

比如说，现在有两个链表，我们需要将它们头尾相连：正常的方法是，我们要先找到一个链表的尾部，然后再将其连到一个拎一个链表的头部，如下图所示

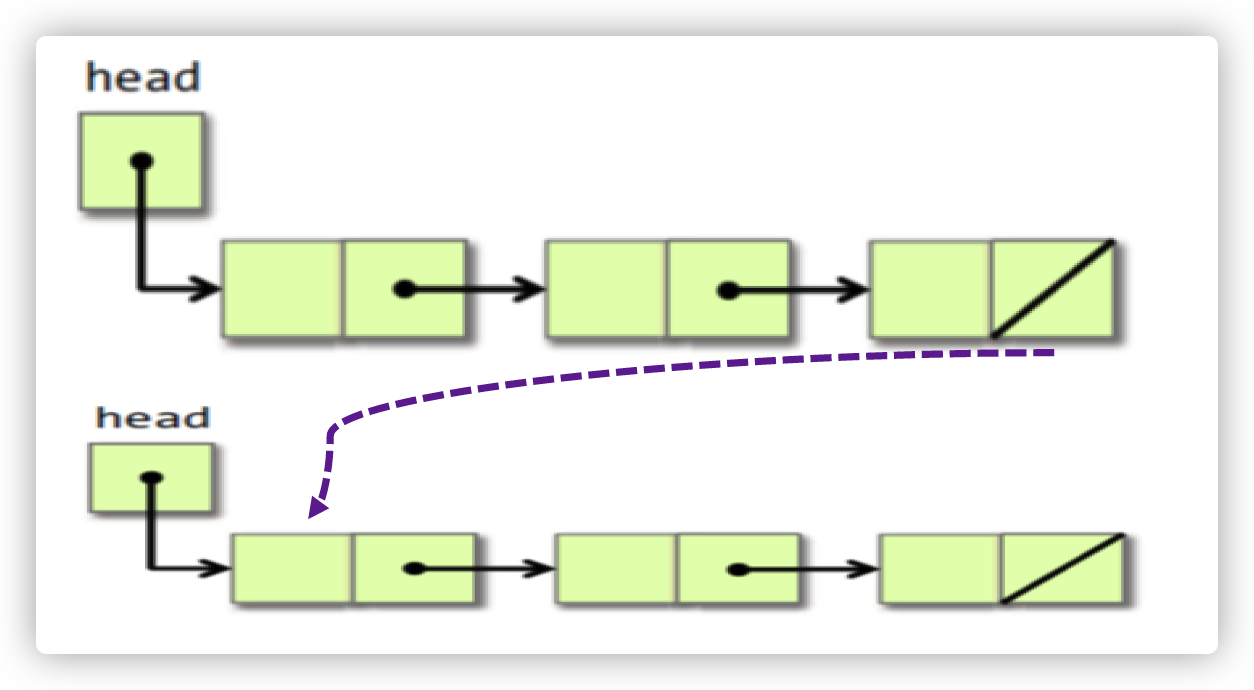
但是，我们可以在链表中添加一点东西，比如说，在head节点添加一个tail指针，让其指向该链表的尾部。这样一来，就可以迅速地找到链表的尾部了，如下图所示：

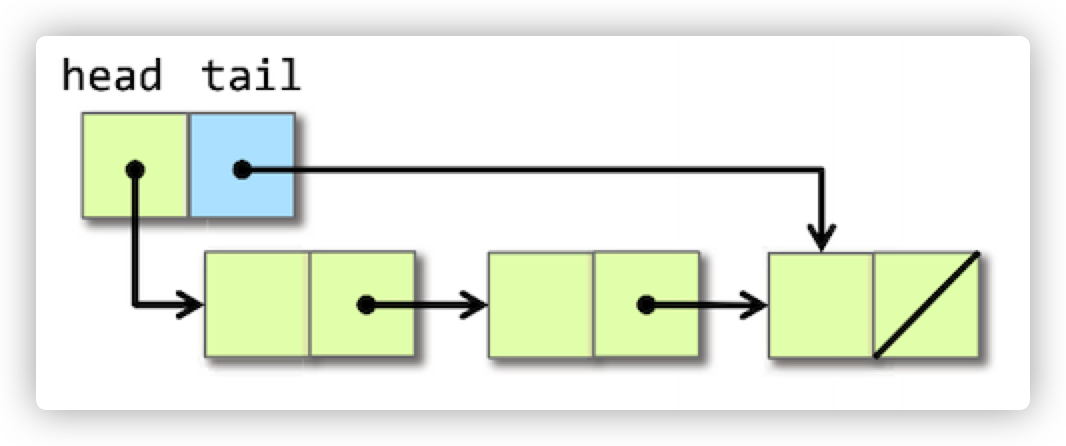
Precomputation 预计算

预计算就是在程序里面先将要算的值存储下来。比如说要计算二项式系数，我们可以用递归的方法来做：

但是递归可能会消耗很多CPU性能，因此我们可以使用动态规划的方法，将预计算得到的值存储起来，如下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# define CHOOSE_SIZE 100
int choose[CHOOSE_SIZE][CHOOSE_SIZE];

void init_choose(){
	for(int n = 0;n < CHOOSE_SIZE ;n++){
		choose[n][0] = 1;
		choose[n][n] = 1;
	}
	
	for(int n = 1;n < CHOOSE_SIZE; ++n){
		choose[0][n] = 0;
		for (int k = 1;k<n;++k){
			choose[n][k] = choose[n-1][k-1]+choose[n-1][k];
			choose[k][n] = 0;
		}
	}
}

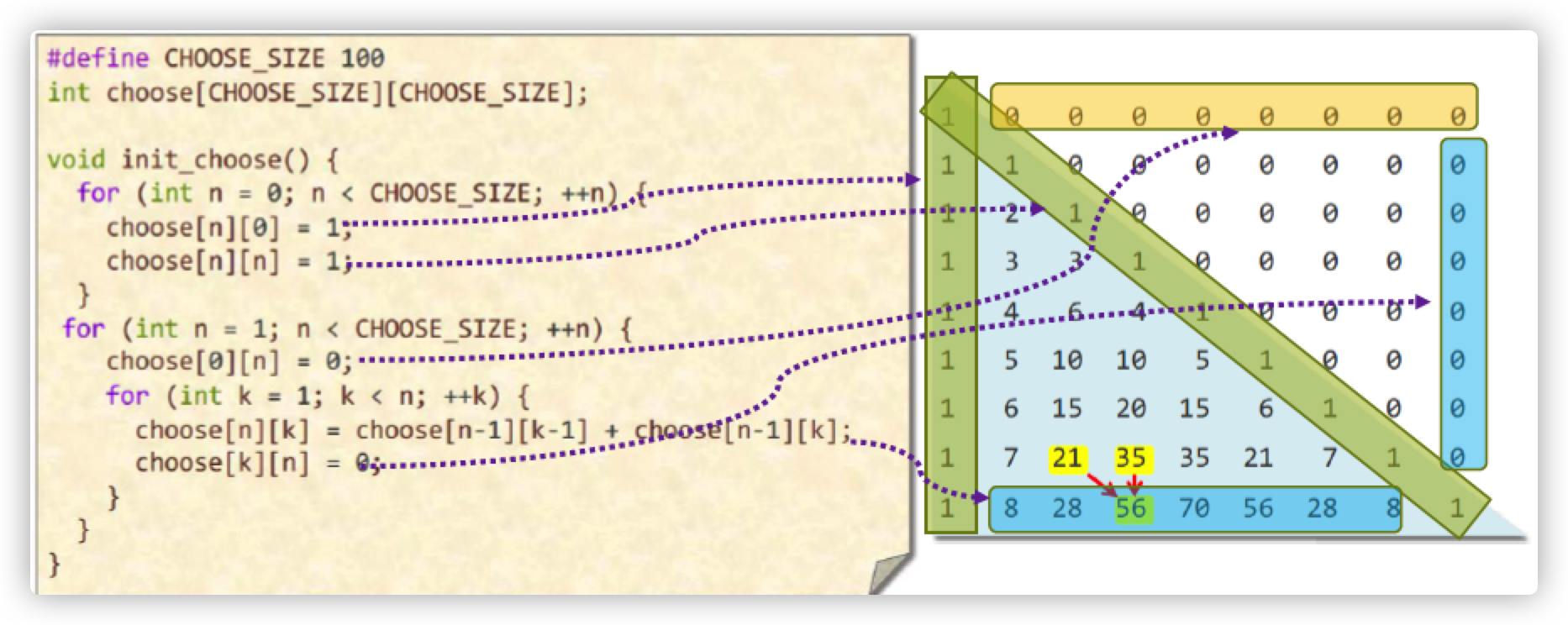
使用了动态规划以后，我们就不用做很深的递归了，只要在数组中取数即可。只要数组规模小于100x100即可

Compile-time initialization 编译时初始化

编译时初始化就是在编译时存储一些常量，这样就可以减少计算的次数。还是以上面的pascal三角形为例，我们可以直接将二维数组存储起来。

元编程

还有一种预计算的方法就是元编程(metaprogramming)。先看看 meta-data：

「我的电话是 +86 123 4567 8910」
——这是一条数据；
「+86 123 4567 8910 有十三个数字和一个字符，前两位是国家代码，后面是一个移动电话号码」 —— 这是关于前面那条数据的数据。

那么照猫画虎，怎样才算 meta-programming 呢？泛泛来说，只要是与编程相关的编程就算是 meta-programming 了——比如，若编程甲可以输出 A - Z，那么写程序甲算「编程」；而程序乙可以生成程序甲（也许还会连带着运行它输出 A - Z），那么编写程序乙的活动，就可以算作 meta-programming，「元编程」。注意，程序甲和程序乙并不一定是同一种语言.

比如说，要生成一张C语言的二维数组，可以这么编写C语言：

1
2
3
4
5
6
7
8
9
10
11
12
int main(){
	init_choose();
	printf("int choose[10][10] = {\n");
	for (int a = 0; a < 10;++a){
		print(" {");
		for (int b = 0;b < 10;++b){
			print("%3d, ",choose[a][b]);
		}
		printf("},\n");
	}
	print("};\n");
}

Caching 缓存

缓存的想法就是将最近访问过的数据放到内存里，这样再次访问时就可以快速从内存里取出，而不用到磁盘里面去找。比如说求平方根的一个函数

1
2
3
inline double hypotenuse(double A,double B){
	return sqrt(A*A+B*B);
}

可以写成是

1
2
3
4
5
6
7
8
9
10
11
12
13
double cached_A = 0.0;
double cached_B = 0.0;
double cached_C = 0.0;

inline double hypotenuse(double A,double B) {
	if (A == cached_A && B == cashed_B){
		return cached_h;
	}
	cached_A = A;
	cached_B = B;
	cached_h = sqrt(A*A + B*B);
	return cached_h;
}

如果缓存能有2/3的概率击中的话，那么就可以第一种方法快30%。但是这种缓存也不是很好，毕竟在现实情况下能击中的概率是很低的，还要进行判断等操作，弄不好就会得不偿失。

Sparsity 稀疏

稀疏矩阵的存储

比如我们要做矩阵-向量乘法，如下：

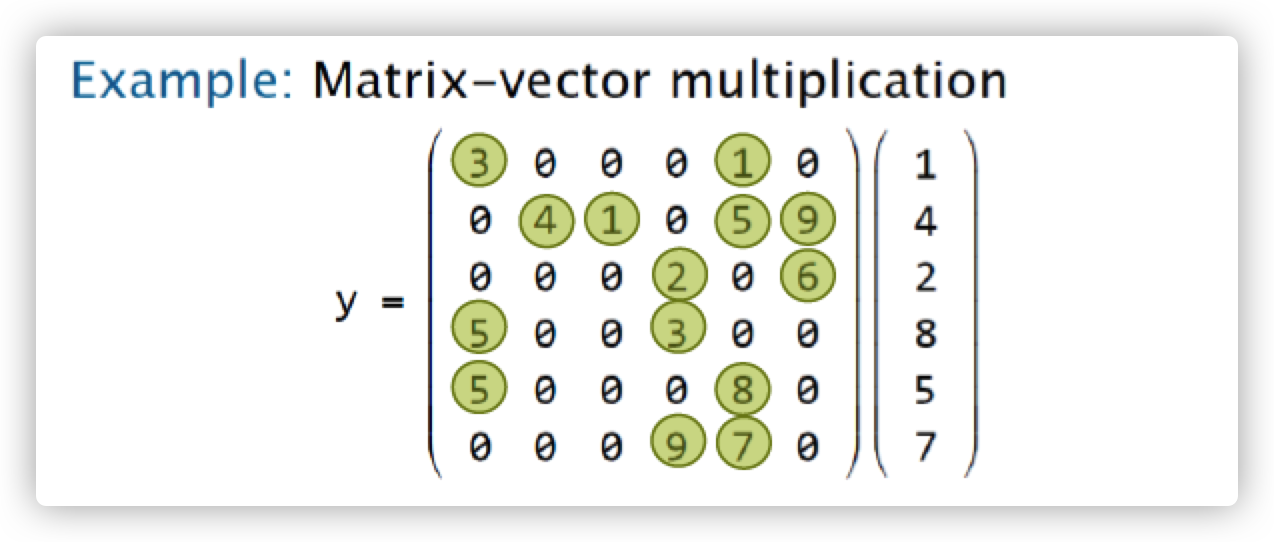
如果我们就这样计算，那么需要计算36次乘法，还要很多次加法。但事实上我们看到系数矩阵有很多的值都是0，有效值只有14个，因此我们可以对其进行压缩。

我们采取CSR的方法，将稀疏矩阵变成这样的形式：

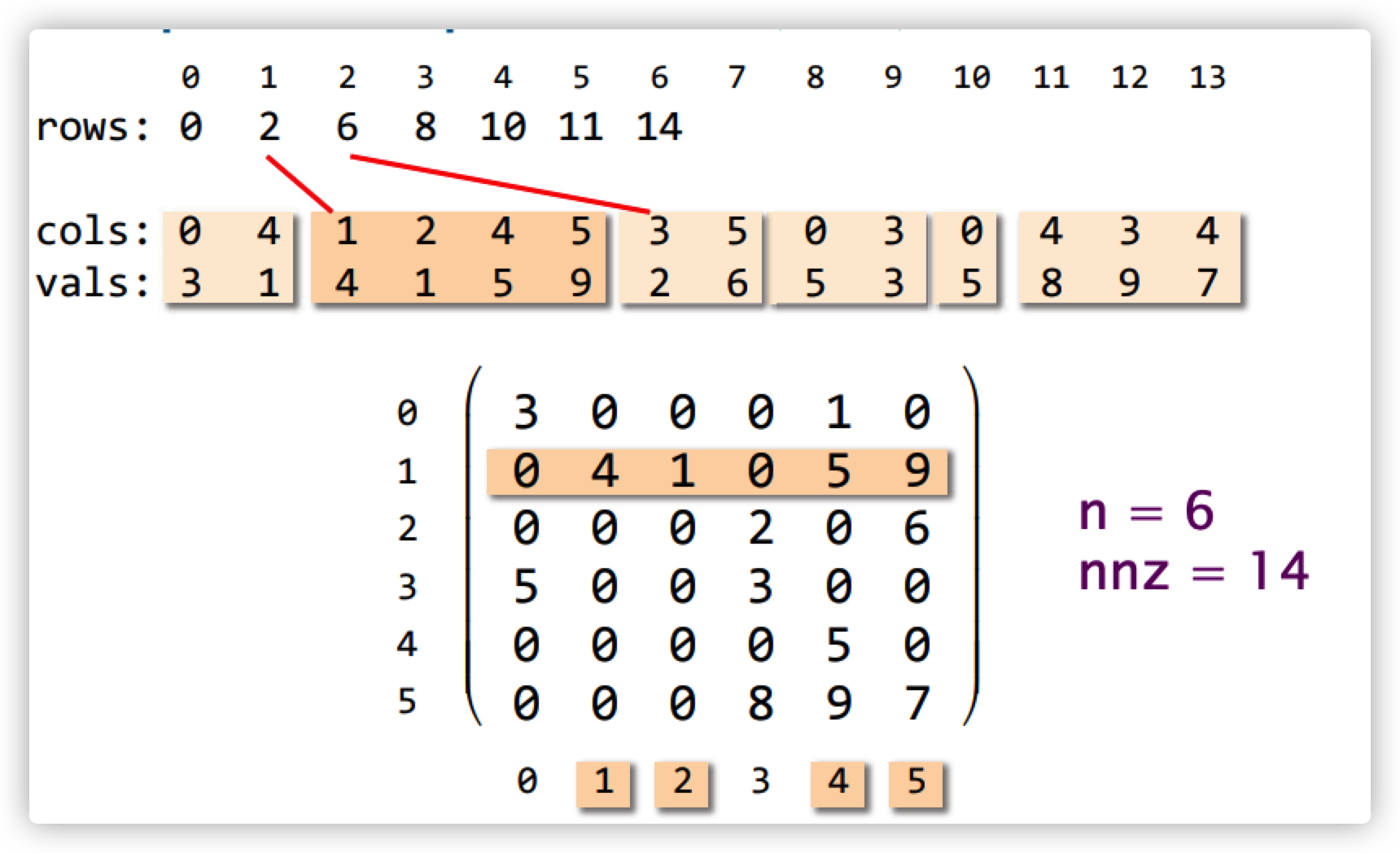
也就是说，采用三个一维数组来存储二维矩阵中的所有非零元素。这三个数组分别为：rows，cols和values。

  • value数组存储所有的非零元素
  • column 数组存储所有非零元素的列下标
  • row 数组存储所有的非零数组的行下标。最原始的存储方式就是：[0,0,1,1,1,1,2,2,3,3,4,5,5,5]。 但是，我们通过row行可以看到，很多重复的数值，也就是每一行的多个元素，每个元素都对应着同样的行号，这样也浪费的空间，因此，我们引入csr稀疏矩阵存储方式，该存储方式将重复的行号压缩，只记录，开头和结尾元素的位置，也就变成了 [0,2,6,8,10,11,14]

其中，nnz就是整个稀疏矩阵中非零值的个数。

这样，存储的空间复杂度就从$O(n^2)$ 变成了 $O(n+nnz)$ ，在n很大的时候，可以有效地减小复杂度。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
typedef struct {
	int n ,nnz;
	int *rows;			// length n
	int *cols;			// length nnz
	double *vals;		// length nnz
} sparse_matrix_t;

void spmv(sparse_matrix_t *A,double *x,double *y) {
	for (int i = 0; i< A-> n ; i++){
		y[i] = 0;
		for (int k = A-> row[i];k<A->rows[i+1];k++){
			int j = A->cols[k];
			y[i] += A->vals[k]*x[j];
		}
	}
}

稀疏图的存储

在数据结构中，通常会用矩阵来存储图。如果这个图的边很少，那么显然这个矩阵就是一个稀疏矩阵了。因此，我们可以用CSR的方法来存稀疏图。如下图所示：

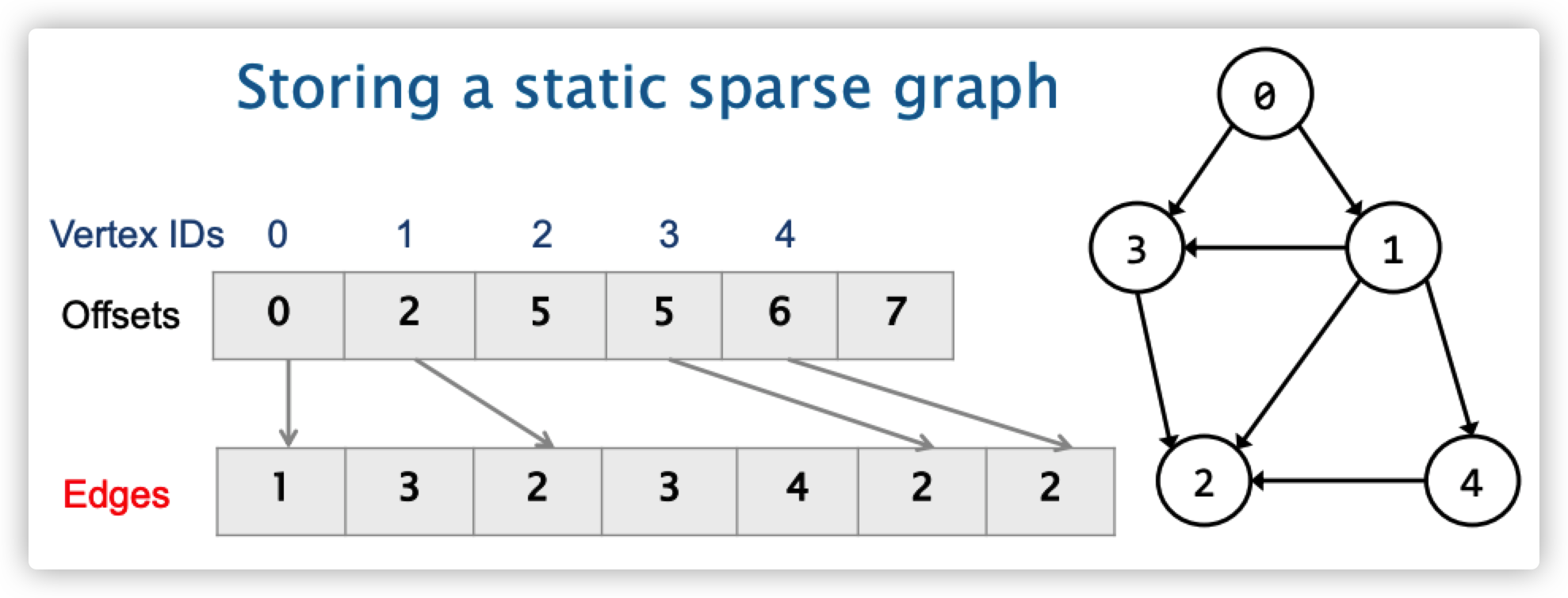
  • 节点0出来，指向1、3

  • 节点1出来，指向2、3、4

  • 节点2没有出度

  • 节点3出来，指向2

  • 节点4出来，指向2

    如果这个边有权重的话，可以再添加一个和Edges长度一样的数组，记录每条边的权重。

Logic

Constant folding and propagation 常量折叠与常量传播

常量折叠与常量传播的想法就是在编译的过程中，用常量表达式去替换在代码中要用到的表达式。

比如下面几个例子，我们已经申请了一系列常量

1
2
3
4
5
6
7
# include <math.h>
void orrery(){
	const double radius = 6371000.0;
	const double diameter = 2*radius;
	const double circumference = M_PI * disameter;
	//...
}

多数的现代编译器不会真的产生计算的指令再将结果储存下来，取而代之的，他们会辨识出语句的结构，并在编译时期将数值计算出来（在这个例子，在处理diameter的时候，就会直接计算得到其值为12742000）

Common-subexpression elimination 公共子表达式消除

公共子表达式消除是一项启发式的查询转换技术，它将反意连接词（如 OR）连接的谓词进行合并，消除不必要的子表达式。如果两个表达式等价但是复杂度不一样，我们就可以用低复杂度的表达式替换掉高复杂度的表达式

任何一个编译器都遵循两个原则：语义等价原则和保守原则。保守原则是说，如果不能确定能不能做，那么编译器就不会去做。

那么我们看到这个例子：

1
2
3
4
a = b+c;											a = b+c;
b = a-d;						——>				b = a-d;
c = b+c;						——> 			c = b+c;
d = a-d;											d = b;

我们可以用赋值语句替换掉原来的加运算。这样可以减少cpu的计算次数。但是要注意，在上例中第三句不能写成是c=a因为在第二句中，b的值进行了修改。

Algebraic identities 代数恒等式

代数恒等式的想法就是将代数等价的低复杂度表达式替换掉高复杂度的式子。

比如说，我要判断两个圆形是否相交，原始的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# include <stdbool.h>
# include <math.h>
typedef struct {
	double x;			// x-coordinate
	double y;			// y-coordinate
	double z;			// z-coordinate
	double r;			// radius of ball
} ball_t;

double square(double x){
	return x*x;
}

bool collides(ball_t *b1, ball_t *b2){
	double d = sqrt(square(b1->x-b2->x)+square(b1->y - b2->y)+square(b1->z-b2->z));
	return d <= b1->r + b2->r;
}

也就是判断一下是否两个球圆心之间的距离是否大于两个球的半径之和。若大于说明未相交，反之则相交

但是这样的代数式比较复杂的，因为sqrt函数会消耗更大的计算机新能。因为$\sqrt u\leq v \text{~~~完全等价于} ~~u\leq v^2$我们可以用更简单的代数恒等式来替代上面这个逻辑：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# include <stdbool.h>
typedef struct {
	double x;			// x-coordinate
	double y;			// y-coordinate
	double z;			// z-coordinate
	double r;			// radius of ball
} ball_t;

double square(double x){
	return x*x;
}

bool collides(ball_t *b1, ball_t *b2){
	double d =  square(b1->x-b2->x)+square(b1->y - b2->y)+square(b1->z-b2->z) ;
	return d <= square(b1->r + b2->r);
}

Short-circuiting 抄近路

Short-circuiting 的想法是当我知道了答案以后，我们就没必要把整套逻辑都做完，直接返回答案即可

比如说：

1
2
3
4
5
6
7
8
9
# include <stdbool.h>
//All elements of A are nonnegative
bool sum_exceeds(int *A,int n,int limit){
	int sum = 0;
	for (int i = 0;i<n;i++){
		sum += A[i];
	}
	return sum > limit;
}

我们可以把最后的判断逻辑放到循环里面，一旦发现sum大于limit，直接跳出循环返回，如下：

1
2
3
4
5
6
7
8
9
10
11
12
# include <stdbool.h>
//All elements of A are nonnegative
bool sum_exceeds(int *A,int n,int limit){
	int sum = 0;
	for (int i = 0;i<n;i++){
		sum += A[i];
		if (sum > limit) {
			return true;
		}
	}
	return false;
}

但是这两个程序都存在明显的逻辑漏洞。因为整数相加后有溢出的风险。

同样的，修改了这个逻辑之后，也不一定会拿到好处。因为我们在每一次循环中都要做if判断，如果前面很多数都很小，没有到达limit，那么程序就会一直执行if判断，运行速度反而会变慢。

Ordering tests 判断条件的顺序

我们知道代码是根据顺序逻辑执行的。 Ordering tests的思想是在很少成功的case之前执行那些更经常“成功”的case（测试选择了特定的替代方案）。同样，代价少的测试应该先于代价高的测试。比如说下面这个例子：

1
2
3
4
5
6
7
# include <stdbool.h>
bool is_whitespace(char c){
	if (c == '\r' || c=='\t' || c==' '||c == '\n'){
		return true;
	}
	return false;
}

在一篇文章里面，最常见的肯定是空格，换行回车符是比较少的。若采用上面这个策略，那么大多数字符要经过前两个比较才能成功判断为空格并退出判断。因此我们可以修改case的顺序：

1
2
3
4
5
6
7
# include <stdbool.h>
bool is_whitespace(char c){
	if (c == ' ' || c=='\r' || c=='\t'||c == '\n'){
		return true;
	}
	return false;
}

这样大多数字符已进入if-case就会落入c==' '的判断并跳出判断，节省了判断次数

Creating a fast path

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# include <stdbool.h>
typedef struct {
	double x;			// x-coordinate
	double y;			// y-coordinate
	double z;			// z-coordinate
	double r;			// radius of ball
} ball_t;

double square(double x){
	return x*x;
}

bool collides(ball_t *b1, ball_t *b2){
	if (
	(abs(b1->x - b2->x)>(b1->r + b2->r))||
	(abs(b1->y - b2->y)>(b1->r + b2->r))||
	(abs(b1->z - b2->z)>(b1->r + b2->r))
	)

	double d =  square(b1->x-b2->x)+square(b1->y - b2->y)+square(b1->z-b2->z) ;
	return d <= square(b1->r + b2->r);
}

Combining tests

Combining tests的想法就是用一个if-case或者switch case 来替换多分支的if判断

比如我们要实现下面这张逻辑表。用if-case 来写，会非常非常复杂：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
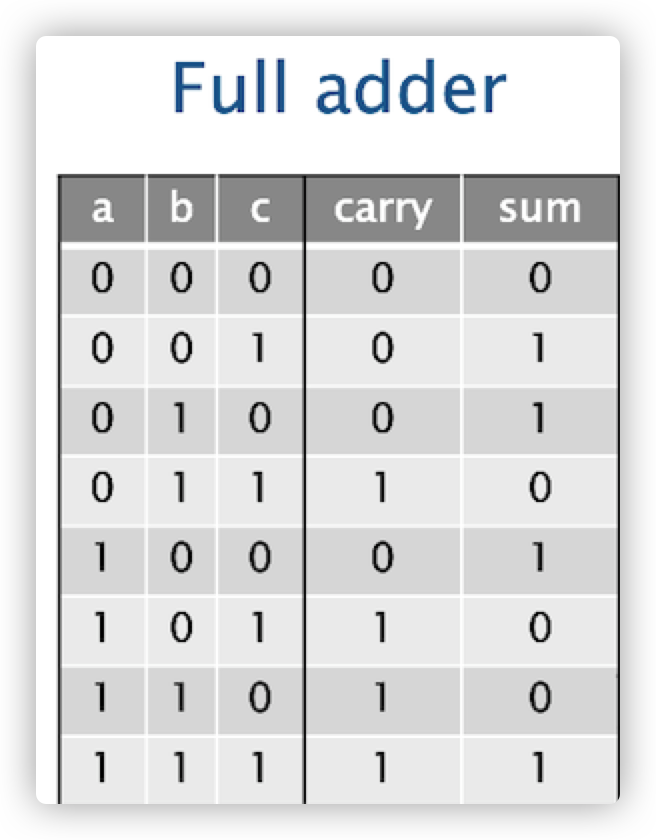
43
void full_add (	int a,
								int b,
								int c,
								int *sum,
								int *carry){
		if( a == 0){
			if(b == 0){
				if(c == 0){
					*sum = 0;
					*carry = 0;
				}else {
					*sum = 1;
					*carry = 0;
				}
			}else {
				if(c == 0){
					*sum = 1;
					*carry = 0;
				}else {
					*sum = 0;
					*carry = 1;
				}
			}else {
				if(b == 0){
					if(c == 0){
						*sum = 1;
						*carry = 0;
					} else {
						*sum = 0;
						*carry = 1;
					}
				}else {
					if (c == 0){
						*sum = 0;
						*carry = 1;
					}else {
						*sum = 1；
						*carry = 1；
					}
				}
			}
		}
}

因为计算机会进行预测，会把预测得到的结果拿到内存里，但是这样的预测的正确性是很低的，因此会导致执行效率大大降低。为了解决这个问题，我们可以采用switch-case

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
void full_add (	int a,
								int b,
								int c,
								int *sum,
								int *carry){
			int text = ((a==1)<<2)((b == 1)<<1)(c == 1);
			switch(text){
				case 0:
					*sum = 0;
					*carry = 0;
					break;
				case 1:
					*sum = 1;
					*carrt = 0;
					break;
				case 2:
					*sum = 1;
					*carrt = 0;
					break;
				case 3:
					*sum = 0;
					*carrt = 1;
					break;
				case 4:
					*sum = 1;
					*carrt = 0;
					break;
				case 5:
					*sum = 0;
					*carrt = 1;
					break;
				case 6:
					*sum = 0;
					*carrt = 1;
					break;
				case 7:
					*sum = 1;
					*carrt = 1;
					break;
			}
}

Loops

Hoisting

hoisting 也叫做循环不变式的代码移动，就是将循环中不变的式子移动到循环外。这样就不用每次循环都进行计算了。比如下面这个例子：

1
2
3
4
5
6
# include <math.h>
void scale(double *X,double *Y,int N){
	for (int i = 0;i<N;i++){
		Y[i] = X[i]*exp(sqrt(M_PI/2));
	}
}

我们发现这个 exp(sqrt(M_PI/2))是一个不变的量，但是放在循环里面每次都要计算一遍，很浪费，所以可以这样改

1
2
3
4
5
6
7
# include <math.h>
void scale(double *X,double *Y,int N){
	double factor = exp(sqrt(M_PI/2))
	for (int i = 0;i<N;i++){
		Y[i] = X[i]*factor;
	}
}

Sentinels 哨兵

哨兵是一些在数据结构中的dummy value，用来简化边界条件的一些逻辑。

这是一个判断是否溢出的程序，如果sum变成了负数，说明溢出了，那么返回真。

1
2
3
4
5
6
7
8
9
10
11
#include <stdint.h>
#includer <stdbool.h>
bool overflow (int64_t *A, size_t n) {
  // All elements of A are nonnegative
  int64_t sum = 0;
  for ( size_t i = 0; i < n; ++i ) {
    sum += A[i];
    if ( sum < A[i] ) return true;
  }
  return false;
}

我们对这个程序进行优化，如果说sum加到最后发现小于A[i]了，说明溢出了，这时候i肯定是小于n的，所以返回true；如果加到A[n-1]之后，没有溢出，那么下一次就落入sum <= A[n]的判断，必为真，此时i=n返回false

我们需要给这个程序添加一个哨兵，也就是 A[n+1]=1 ，为了防止 A[0]到A[n-1]都是0的情况。否则加到A[n]后无法跳出循环，设定 A[n+1]=1 是为了sum=INT64_MAX之后再+1变为负值，跳出循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <stdint.h>
#includer <stdbool.h>
//  Assumes that A[n] and A[n+1] exist and can be clobbered
bool overflow (int64_t *A, size_t n) {
  // All elements of A are nonnegative
  A[n] = INT64_MAX;
  A[n+1] = 1;
  size_t i = 0;
  int64_t sum = A[0];
  while( sum >= A[i]){
  	sum += A[++i];
  }
  if (i <n) return true;
  return false;
}

Loop unrolling 循环展开

循环展开尝试在一次迭代中执行多次迭代的内容。因此可以减少迭代的次数，因为迭代的过程需要消耗更多的机器指令。并且能让编译器优化更多内容。

但是，也不要展开太多。否则会导致指令缓存的滥用。因此，我们有两种展开方式，全展开和部分展开

Full Loop unrolling

所有循环展开对于次数不多的循环是有效的，比如：

1
2
3
4
int sum = 0;
for (int i = 0;i<10;i++){
	sum += A[i];
}

可以换成：

1
2
3
4
5
6
7
8
9
10
11
12
int sum = 0;
sum += A[0];
sum += A[1];
sum += A[2];
sum += A[3];
sum += A[4];
sum += A[5];
sum += A[6];
sum += A[7];
sum += A[8];
sum += A[9];
sum += A[10];

Partial Loop unrolling

部分循环展开更好一些，我们可以这样写：

1
2
3
4
5
6
7
8
9
10
11
int sum = 0;
int j ;
for(j = 0;j < n-3;j+=4){
	sum += A[j];
	sum += A[j+1];
	sum += A[j+2];
	sum += A[j+3];
}
for (int i = j ; i< n;++i){
	sum += A[i]
}

Loop fusion 循环融合

Loop fusion是将循环次数相同的若干循环给放到一个循环当中，同样是用来减少循环次数

1
2
3
4
5
6
7
for (int i = 0;i<n;++i){
	C[i] = (A[i] <= B[i])? A[i]:B[i];
}

for (int i = 0;i<n;++i){
	D[i] = (A[i] <= B[i])? B[i]:A[i];
}

可以把上述两个循环合并

1
2
3
4
for (int i = 0;i<n;++i){
	C[i] = (A[i] <= B[i])? A[i]:B[i];
	D[i] = (A[i] <= B[i])? B[i]:A[i];
}

Eliminating wasted iteration

消除多余迭代同样是要减少迭代的次数。比如说在下面这个例子中，我们可以将双重循环和ifcase结合起来

1
2
3
4
5
6
7
8
9
for (int i = 0;i<n; ++i){
	for (int j = 0;j < n; ++j){
		if(i > j){
			int temp = A[i][j];
			A[i][j] = A[j][i];
			A[j][i] = temp;
		}
	}
}

可以写成是：

1
2
3
4
5
6
7
for (int i = 1;i < n;++i){
	for (int j = 0;j<i;++j){
		int temp = A[i][j];
		A[i][j] = A[j][i];
		A[j][i] = temp;
	}
}

Functions

Inlining 内联函数

内联函数也是在编译上下功夫，和宏不一样，宏是直接替换代码，不做语义上的检测。但是内联函数的话，编译器会在编译时进行语义上的检测，比用宏更加安全。

比如说：

1
2
3
4
5
6
7
8
9
10
11
double square (double x){
	return x*x;
}

double sum_of_squares (double *A,int n){
	double sum = 0.0;
	for (int i = 0;i<n;++i){
		sum += square(A[i]);
	}
	return sum;
}

可以将square变成内联函数，可以在编译时进行替换。减少调用所花费的指令

1
2
3
double inline square (double x){
	return x*x;
}

Tail-recursion elimination

Coarsening recursion

-------------本文结束，感谢您的阅读-------------