抽样算法
在聊抽样算法之前,我们首先谈一下样本。
样本是总体的一个子集,对其进行观察以获得关于总体的信息。研究样本的目的在于得到有关总体的有效结论(概率论中学过,详见参数估计博客)
常见的抽样技术有:
- 简单随机抽样
- 系统抽样
- 分层抽样
- 聚类抽样
- 多阶段抽样
所有的这些方法都属于概率抽样
常见抽样
简单随机抽样
这是最简单的抽样算法。
在抽样过程中,若是有放回的抽样统计,那么选择每个对象的概率是相同的。
如果是无放回的抽样统计,在总体容量很大的时候,无放回抽样可以近似看做是等概率抽样。
方法: 令N 为总样本数,$X_i$ 为一随机变量。
其中$P(X_i=1)=p$ ,为抽样率
系统抽样
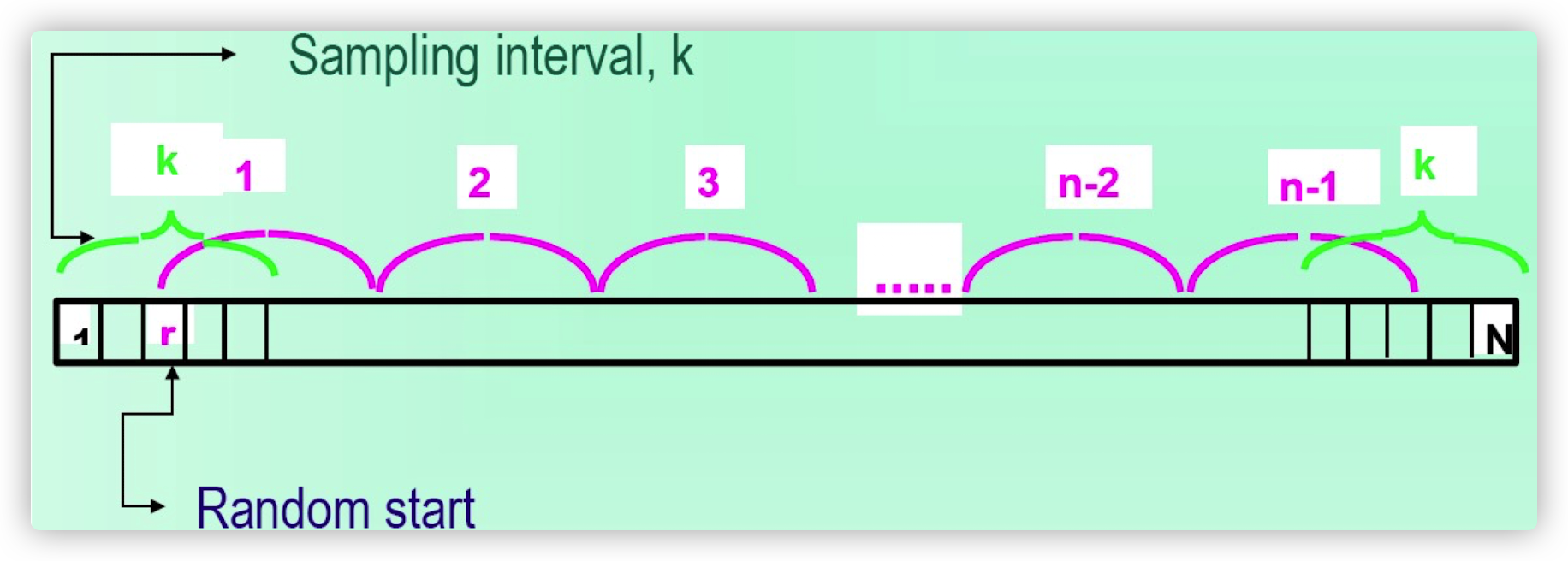
假设我们要从容量为N的总体中抽取容量为n的样本,有两种系统抽样的策略:
直线等距抽样
如果N能被n整除
- 那么就可以确定样本大小n并计算跳跃间隔 $k = \frac{N}{n}$
- 在1到k之间(包含1和K)随机选择一个起始点r。
- 然后,反复地在选定第$(r+k\cdot i)$ 个样本点,其中,$i = 1,2\cdots,n-1$
相当于总体被分为n组,然后每组有k个样本,每个样本点被选择的概率为$\frac{1}{k}$
在这种情况下,线性系统抽样方法是等概率的。
但N如果不能被n整除
- 最后一组样本点个数不及k个
- 此时系统抽样就不是等概率的了。
循环系统抽样
首先确定间隔 k, 使得 $k = \lfloor\frac{N}{n}\rfloor$
从1到N之间随机开始,选择第$(r+k\cdot i)/\mod N$,知道选择了n个样本为止。
- 因此,可能选择N个不同的样本集,而不是k个
- 在此时,这种抽样方法也是一种等概率抽样。
系统抽样有以下优缺点:
- 优点
- 操作简单,容易取样
- 它使样本更均匀地分布在总体中
- 比简单随机抽样更有效,尤其是当列表中的样本点顺序与关注变量的特征无关时
- 缺点
- 一个不好的样本点排列可能会产生一个不具有代表性的样本集。比如我要统计公园一年来的客流量,那么如果起始点抽到了礼拜六,间隔又是一个礼拜,那么显然我采样得到的客流量要比平均客流量要多很多。
- 非严格等概率抽样,抽样误差计算复杂
分层抽样
分层抽样是根据某种属性(比如性别、职称、院系、地域等)将总体分为多个不同的组。
然后,由满足分层变量值设定条件的样本点组成
这样做的好处是
- 减少估计的标准误差
- 提供总体不同组别的单独估计(“域”估计)
- 对不同组别,可以使用不同的抽样方法并行地提高抽样效率
样本量分配方法
水库抽样
水库抽样是一种针对流数据的高效等效率抽样方法
我们想象流数据应用场景:谷歌搜索引擎的关键词查询,电信骨干网络中转发的数据包。
那么如果想从流数据中抽取容量为1000的样本,怎么办?这是比较困难的,因为在流数据应用场景中,总体容量是无法事先知晓的。另外,可能需要随时返回样本。
现在,我们来介绍水库抽样:
首先,创建一个长度为1000的数组,作为水库。如果流数据不超过1000个元素,每个元素都存入该数组中。
那么,处理第i(i>=1001)个元素,该如何做?
例子
设 $S = {59,100,2,30,63,\cdots}$ 且$k=3$
前k个项直接添加到水库中,即样本集合为 ${59,100,2}$
当第4个元素30到达时,程序会随机生成一个1到4之间的随机整数,假定生成随机数$x=4$, 因为 $x>k$ ,则钙元素直接被忽略。
当第5个元素63到达时,程序会随机生成一个1到5之间的随机整数,假定生成随机数$x=2$,因为$x<k$ ,元素63直接替换水库中的第2个元素100. 因此,最终的样本集合为${59,63,2}$
分布式水库抽样方法
假如说,利用多台机器,能否加快水库抽样的速度呢?水库抽样是否可以扩展成分布式算法呢?
我们可以在每台机器上维护同样大小的水库,分别执行水库抽样算法。然后,对每个水库的样本进行重抽样,逻辑如下:

分布式水库抽样算法也非常高效,时间复杂度为$O(1)$
分布式水库抽样中,每个元素被重样的概率是相同的,且任意两个元素被抽样是相互独立的。
例题
1
设总体有14个个体,按照1~14进行编号。欲以系统抽样法抽取容量为 $n=4$ 的样本,且第一个抽中的样本编号为1,则其余3个样本编号为多少?
这是系统抽样问题
首先,我们要计算间隔 $k = \lfloor \frac{14}{4} \rfloor = 3$ ,也就是要跳跃3个样本取下一个样本,因此取 $1,5,9,13$
2.
某校高一年级500名学生中,血型为O的有200人,血型为A的有125人,血型为B的有125人,血型为AB型的有50人.为了研究血型与色弱的关系,要从中抽取一个容量为40的样本,应如何抽样?写出血型为AB型的抽样过程.
这是分层抽样算法
首先,在500名学生中取40名样本,概率为 $\frac{2}{25}$
所以,应用分层抽样法抽取
- 血型为O型的: $\frac{2}{25}\times 200 = 16$
- 血型为A型的: $\frac{2}{25}\times 125 = 10$
- 血型为B型的: $\frac{2}{25}\times 125 = 10$
- 血型为AB型的: $\frac{2}{25}\times 50 = 4$
AB型的4人可以这么抽取:
第一步:将50人随机编号,1~50
第二步:把以上50人的编号分别写在号签上
第三步:从袋子里抽取四个号签,找出对应的4人。
其余血型的人也可以用这种方法来抽取。