数据科学与工程算法-哈希算法
引入
首先我们提出两种情境:
- 判断用户名是否被注册
我们当然可以对用户名建立B+树索引,这样可以提高查询效率,复杂度为$O(\ln n)$ ,其中n为集合大小。
但是我们能不能找到$O(1)$复杂度的方法呢?
- 文本冗余检测
假设我们有搜索引擎定期爬取网页内容,但是爬取太多冗余文本会浪费存储空间。然而,将海量文本逐篇对比过于低效了,如何判断网页的内容是否冗余呢?
哈希函数我们都不陌生,用数学公式来表达就是:
用图片来显示就是: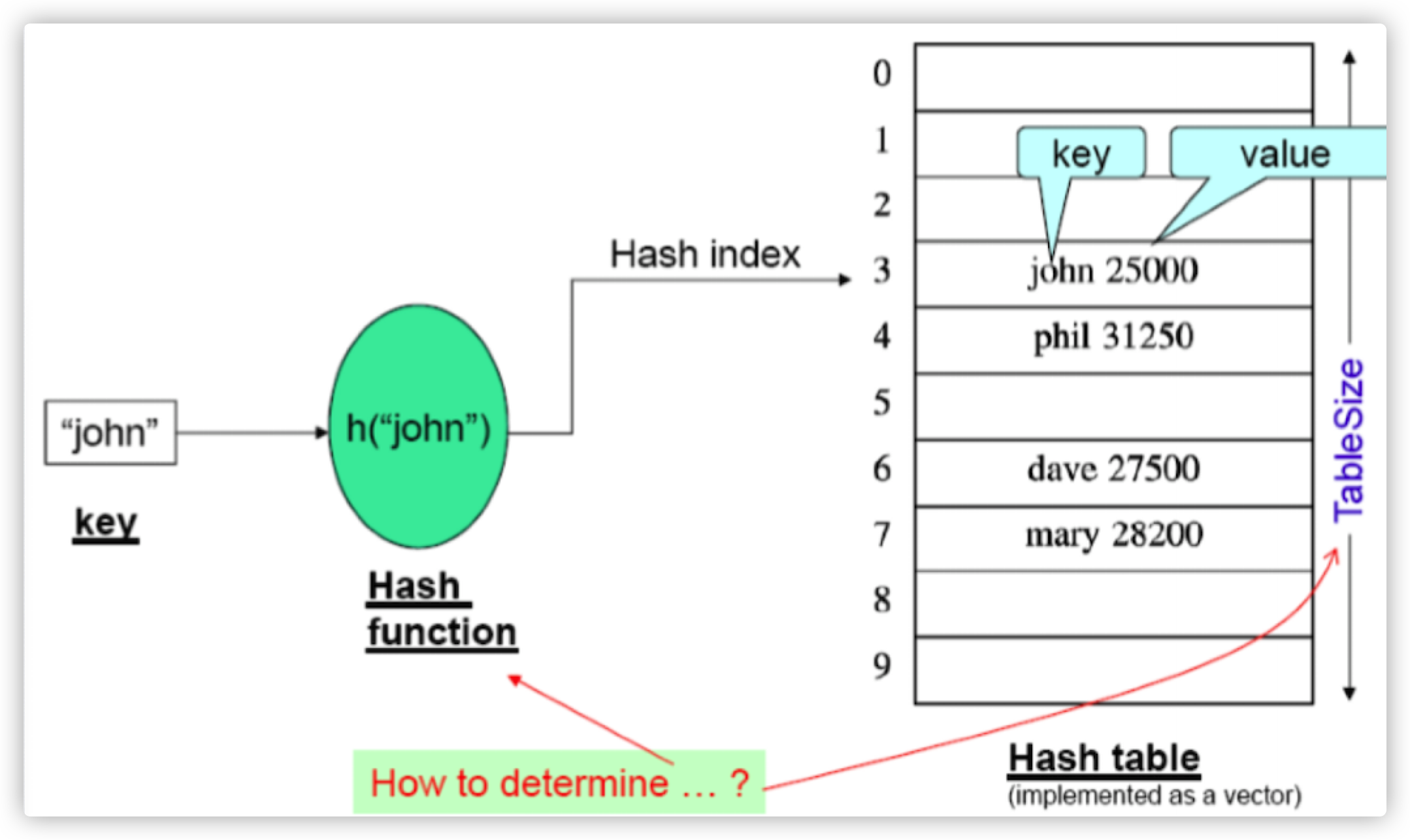
哈希函数的作用:
- 压缩存储:哈希值所需的存储空间远小于输入关键词占用的空间
- 网页URL哈希到某个未知,可以表示为一个整数
- 邮件地址哈希成一个整数
- 无冲突:理想状态下,输入不同的关键词会得到不同的哈希值
- 即使是两个差异很小的关键词也会得到两个完全不同的哈希值
- 相同关键词被相同哈希函数哈希,不可能得到两个不同的值
- 不可逆:在不知道哈希函数的情形下,仅知道哈希值,不可能轻易地猜到此哈希值对应的关键词
- 唯一找到关键词的方法是暴力算法
- 正是因为这一点,哈希函数称为最重要的密码学工具之一
哈希表性能
- 哈希函数:将冲突最小化,使得key和value均匀地分布在整个表中
- 冲突解决策略:将key/value存储在不同的位置,或将多个key/value用链表串起来
- 哈希表大小:表过大会降低碰撞的可能,单会造成内存空间的浪费。过小的哈希会增加碰撞的可能性
布隆过滤器
布隆过滤器是为了应对碰撞而提出的一种高空间效率的概率数据结构,用于判断一个元素是否属于一个集合的成员。
布隆过滤器有广泛的应用:
- 垃圾邮件地址过滤器:可以有效过滤垃圾邮件地址
- 拼写检查:能很快发现文字编辑软件中输入的错
- 重复检查:用于网络爬虫判断某个URL是否已经被爬取过了,或用户名是否被注册过
那么布隆过滤器是怎么被提出的呢?我们已经知道哈希面临的问题是冲突,假设哈希函数是良好的,那么如果我们的位阵列长度为m个点,那么如果我们想将冲突率降低到例如 $1\%$ ,这个散列表就只能容纳 $m/100$ 个元素。显然这很浪费空间效率。解决的办法也很简单,就是使用多重哈希,如果他们有一个判断出元素不在集合中,那肯定是不在的;如果它们都说在,虽然也有一定的可能性它们在说谎,不过直觉上判断这种事情的概率是比较低的。这就是布隆过滤器。
优点
它的优点是空间效率和查询时间都比一般的算法要好的多。隆过滤器存储空间和插入/查询时间都是常数。另外, Hash函数相互之间没有关系,方便由硬件并行实现。布隆过滤器不需要存储元素本身,在某些对保密要求非常严格的场合有优势。
缺点
但是布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加,误算率随之增加。常见的补救办法是建立一个小的白名单,存储那些可能被误判的元素。但是如果元素数量太少,则使用散列表足矣。
另外,一般情况下不能从布隆过滤器中删除元素。我们很容易想到把位列阵变成整数数组,每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。
示例
假定集合中有n个元素,位数组初始长度为m,每个位置都被置为0,那么给定一组k个哈希函数 $h_1,\cdots,h_k$ ,其中$h_i$ 的范围为${0,\cdots,m-1}$ ;这个例子中 $m=18,k=3$
那么我们要插入三个元素${x,y,z}$ ,每个元素就会被哈希到位数组中的三个位置。如下图所示:
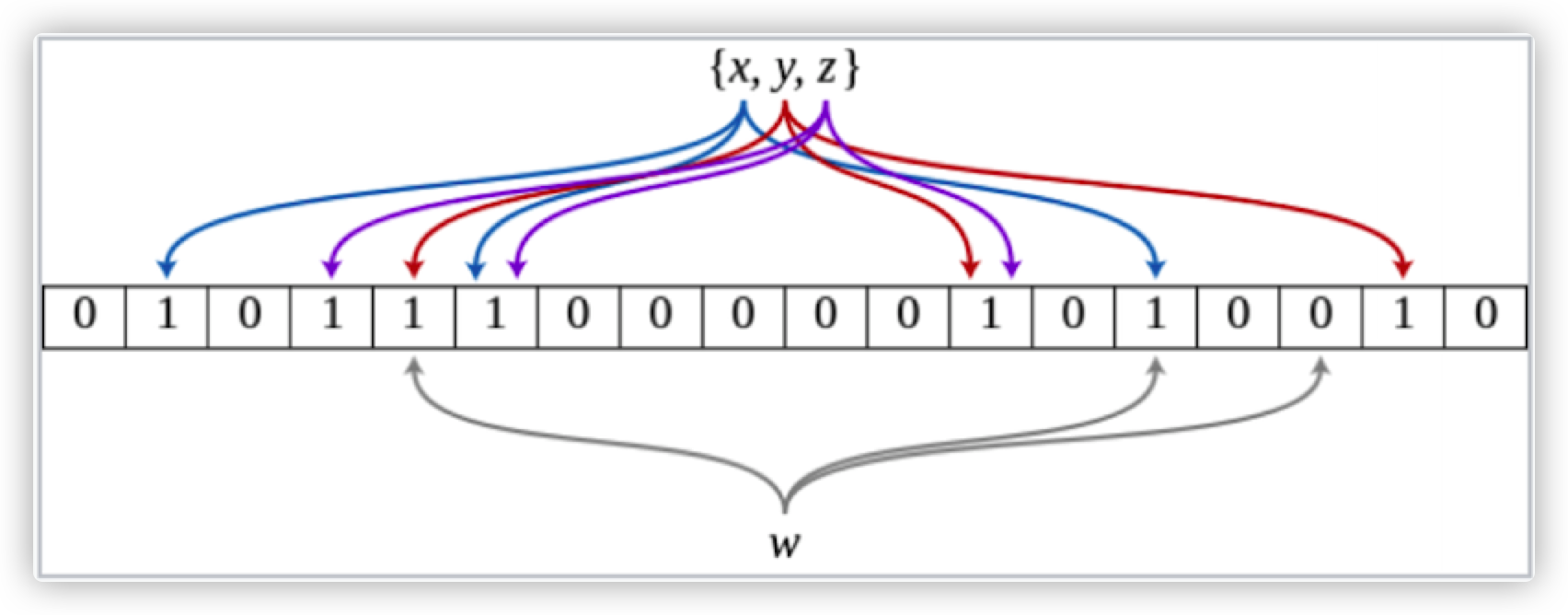
元素插入
现在我们约定3个哈希函数$h_1,h_2,h_3$,其中$h_i$的范围为 ${0,1,\cdots,9}$ ,初始状态长度为10 的位数组每个位置为置为0.

然后,元素$x_1$被映射到了 ${1,4,9}$, 于是将1、4、9都改成1

接着元素$x_2$被映射到了${4,5,8}$, 于是4、5、8置为1,因为4已经是1了,所以不变

元素查询
现在位数组中存放着两个元素,我们要查询的时候,流程如下:
- 查询 $y_1$, $H(y_1)= {1,4,9}\longrightarrow Yes$
- 查询 $y_2$, $H(y_2) = {0,4,8}\longrightarrow No$
- 查询$y_3$, $H(y_3)={1,5,8}$ 这并不是存入的元素,但是在1、5、8这三个位置上的值却都是1,因此出现了假阳性的情况
所以说,布隆过滤器会出现误判的情况:
- 虽然不会出现拒真的情形(假阴性不会出现 ), 是真的不会给你判成假的
- 但是可能会出现纳伪的情形(假阳性)
误判率分析
当插入一个元素到布隆过滤器,一个哈希函数未将某个特定位置置为1的概率为 $1-\frac{1}{m}$
当一个元素插入布隆过滤器后,k个哈希函数未将特定位置置为1的概率为 $(1-\frac{1}{m})^k$
将n个元素插入布隆过滤器后,特定位置未被置为1的概率为 $(1-\frac{1}{m})^{kn}$
因此,某个特定位置为1的概率为 $(1-(1-\frac{1}{m})^{kn})$
现在,在查询某个元素的时候,当k个哈希函数对应的位置均为1,则过滤器声称该元素属于该集合。但如果这个元素不属于集合,就会发生误判。其概率是:
可以近似是因为极限:
从这个概率可知:
- 误判概率随着布隆过滤器位数组的长度m的增大而减小
- 随着更多元素的加入,误判概率随元素个数n的增加而增加
那么如何降低误判概率呢?
- 集合中元素个数相对固定,空间大小可能受限
- 可以通过适当选择哈希函数的个数即k值来最小化概率$(1-e^{-\frac{kn}{m}})^k$
局部位置敏感哈希(LSH)
现在有一个情境,就是对冗余文本的检测,将文章一一对比查找在性能上肯定说不过去。因此我们可以将文本分块, 然后将相似的块大概率会被哈希到同一个桶中,而不相似的文档大概率会被哈希到不同的桶中。到时候,我们就只在一个桶里进行比较就可以了。
利用这种技术,我们可以用来做抄袭检测、镜像网站的发现。
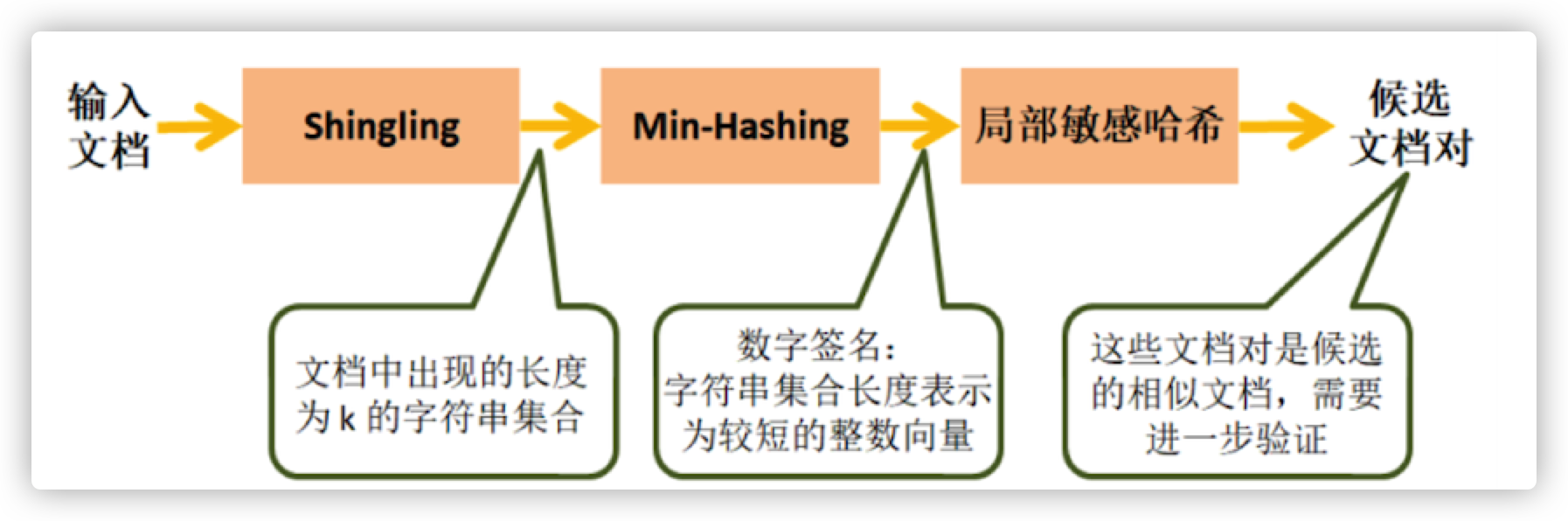
局部位置敏感哈希可以用来在海量文档中查找其中的冗余文本。步骤如下:
- Shingling :将文档转换为集合
- Min-Hashing:将大的几何转换为短的签名,同时保留相似性
- 局部敏感哈希:筛选或寻找相似文档候选对
Jaccard相似度
给定集合A和B,Jaccard相似度定义为:
给定集合A和B,Jaccord距离定义为:
Jaccard 相似度可以用来衡量文本之间的相似度
Shingling文档的集合表示
首先,要对文本建模。
- 定义Document为文档出现的单词集合
- 因为简单的分词会损失上下文信息,那么为了关注单词的顺序,我们需要定义Shingles
文本中的 K-Shingles 是文本中连续k个token(字符、单词等)组成的序列。比如说,给定字符串 D = abcab,令k=2,则字符串的2-Shingles为
如果k-Shingles看做是multiset(可重复),那么
当我们得到了两个文档的$S(D)$ 之后,我们就可以计算器Jaccord相似度.但是,当文档数量非常庞大时(假设为1000000),那么待计算相似度的文档对有:
计算机需要非常长时间才能进行如此庞大的计算。因此,我们需要在得到了k-Shingling之后,运用某个哈希函数将长度为k的字符串映射为桶编号。进一步将一系列集合表示成特征矩阵。其中,每行代表一个桶,每列代表一个文档。给定4篇文档:其转换图如下
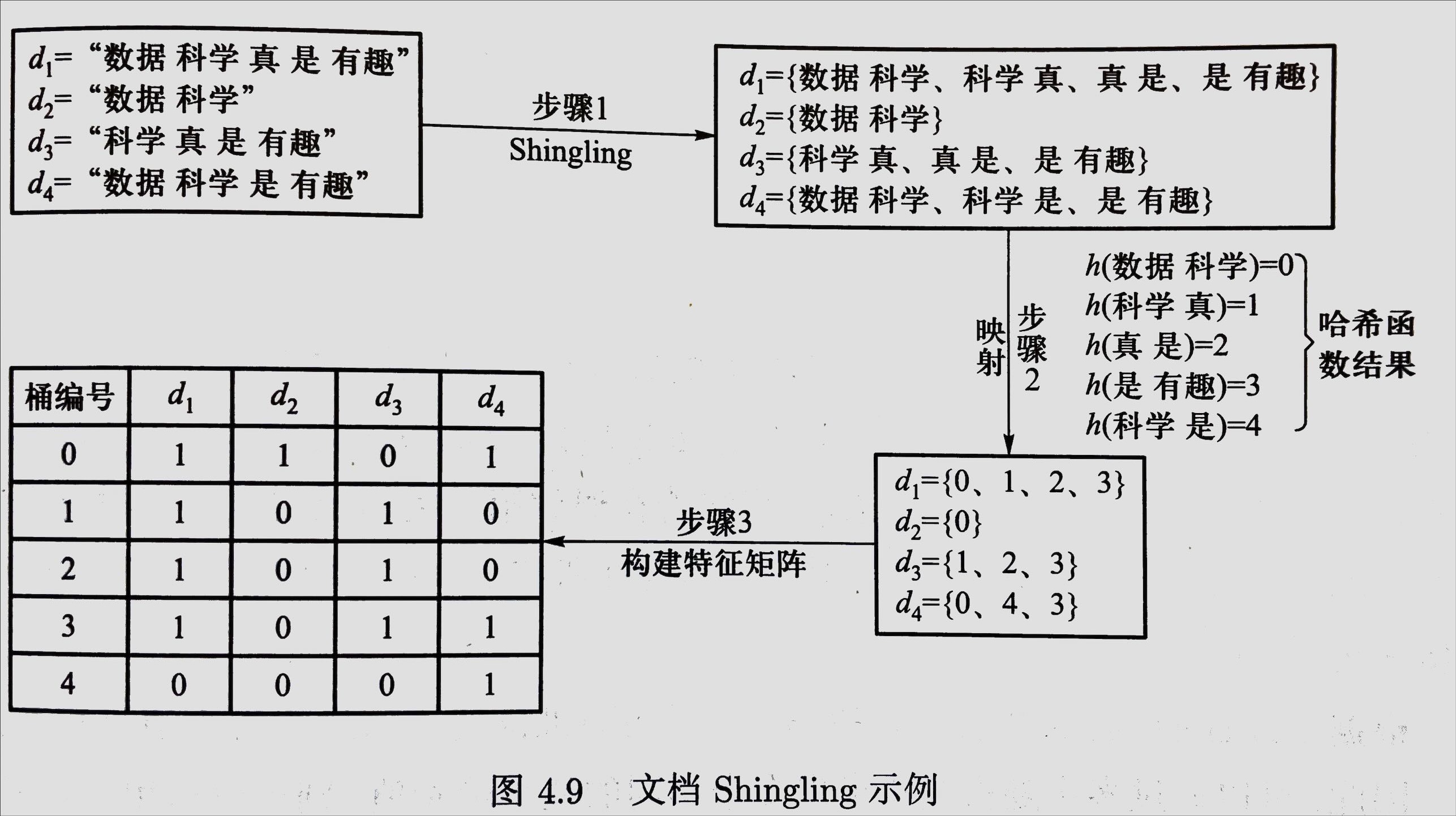
Min-Hashing
最小哈希是一类特殊的哈希函数。其定义:
给定布尔向量$\bold{v}$ 和随机排列$h$ ,$h(v)$ 为布尔向量$\bold{v}$ 经过随机排列后得到的新向量,$mh(\bold{v})$ 为新得到的布尔向量$h(\bold v)$ 中第一个不为0的行号。函数$mh(\bold v)$被称为是最小哈希函数
比如说,我将上面这个表格打乱,得到:
| S1 | S2 | S3 | S4 | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 | 0 |
| 4 | 1 | 1 | 0 | 1 |
这里打乱之后,行号仍然按顺序标注,否则打乱就没有意义了。
按照竖着来看,$mh(\bold{v})$ 为新得到的布尔向量$h(\bold v)$ 中第一个不为0的行号。因此可以求出每个个文档的最小哈希值分别为:
最小哈希与Jaccard相似度
现在我们可以证明:在经过打乱后的两个集合计算得到的最小哈希值相等的概率,是等于这两个集合的Jaccard相似度的。
我们仅考虑集合S1和S2 这两列.那么这两列所在的行有以下三种类型:
- 这一行的S1和S2都为1,记为X类
- 这一行只有一个值为1,一个值为0,记为Y类
- 这一行两个值都为0,记为Z类。
假设属于X类的行有x个,属于Y类的行有y个,所以S1和S2交集的元素个数为x,并集的元素个数为x+y,所以$Jaccard(S_1,S_2) = \frac{x}{x+y} $
接下来计算最下哈希$h(S_1)=h(S_2)$ 的概率,经过打乱之后,对特征值从上往下进行扫描,在碰到Y类行之前碰到X行的概率为$\frac{x}{x+y}$; 又因为X类行中$h(S_1)=h(S_2)$ ,所以$h(S_1)=h(S_2)$的概率为$\frac{x}{x+y}$,即这两个集合Jaccard相似度。
因此,我们可以通过多次随机重排来求出多个不同的最小哈希值,则可以运用$mh(S_1)=mh(S_2)$ 发生的频率估计事件 $mh(S_1)=mh(S_2)$ 发生的概率。
由此我们来引出最小哈希签名:
最小哈希签名
上面是用一个行打乱来处理特征矩阵,然后就可以得到每个集合最小哈希值,这样多个集合就会有多个最小哈希值,这些值就可以组成一列
当我们用多个随机行打乱(假设为n个,分别为$h_1,h_2\cdots h_n$)来处理特征矩阵时,然后分别计算打乱后的这n个矩阵的最小哈希值;这样,对于集合S,就会有n个最小哈希值,这n个哈希值就可以组成一个列向量,为$[h_1(S), h_2(S)\cdots h_n(S)]$;
因此对于一个集合,经过上面的处理后,就能得到一个列向量;如果有m个集合,就会有m个列向量,每个列向量中有n个元素。把这m个列向量组成一个矩阵,这个矩阵就是特征矩阵的签名矩阵;
这个签名矩阵的列数与特征矩阵相同,但行数为n,也即哈希函数的个数。
通常来说,n都会比特征矩阵的行数要小很多,所以签名矩阵就会比特征矩阵小很多。
最小哈希签名矩阵的计算
现在我们来举一个具体的计算样例来理解最小哈希签名
首先我们用n来代表哈希函数的个数,通过哈希函数,我们可以来模拟行打乱的效果。
令$SIG(i,c)$表示签名矩阵中第$ i$ 个哈希函数在第$c$列上的元素。开始时,将所有的$SIG(i,c)$初始化为 Inf(无穷大),然后对第r行进行如下处理:
- 计算$h_1(r), h_2(r)\cdots h_n(r)$;r为行数
- 对于每一列c:
- 如果c所在的第r行为0,则什么都不做;
- 如果c所在的第r行为1,则对于每个$i=1,2\cdots ,n$,将SIG(i,c)置为原来的$SIG(i,c)$和$h_i(r)$之间的最小值。
例如,考虑上面的特征矩阵,将abcde换成对应的行号,在后面加上两个哈希函数,其中$h_1(x)=(x+1) \mod 5\h_2(x) = (3\cdot x+1) \mod 5$,注意这里x指的是行号:
| s1 | s2 | s3 | s4 | h1 | h2 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 2 | 4 |
| 2 | 0 | 1 | 0 | 1 | 3 | 2 |
| 3 | 1 | 0 | 1 | 1 | 4 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 | 3 |
接下来计算签名矩阵。一开始时,全部初始化为Inf:
| s1 | s2 | s3 | s4 | |
|---|---|---|---|---|
| h1 | Inf | Inf | Inf | Inf |
| h2 | Inf | Inf | Inf | Inf |
接着看特征矩阵中的第0行;这时S2和S3的值为0,所以无需改动;S1和S4的值为1,需改动。h1= 1,h2= 1。1比Inf小,所以需把S1和S4这两个位置对应的值替换掉,替换后效果如下:
| s1 | s2 | s3 | s4 | |
|---|---|---|---|---|
| h1 | 1 | Inf | Inf | 1 |
| h2 | 1 | Inf | Inf | 1 |
接着看第1行;只有S3的值为1;此时h1= 2,h2= 4;对S3那一列进行替换,得到:
| s1 | s2 | s3 | s4 | |
|---|---|---|---|---|
| h1 | 1 | Inf | 2 | 1 |
| h2 | 1 | Inf | 4 | 1 |
接着看第2行;S2和S4的值为1;h1=3,h2=2;因为签名矩阵S4那一列的两个值都为1,比3和2小,所以只需替换S2那一列:
| s1 | s2 | s3 | s4 | |
|---|---|---|---|---|
| h1 | 1 | 3 | 2 | 1 |
| h2 | 1 | 2 | 4 | 1 |
接着看第3行;S1,S3和S4的值都为1,h1=4, h2= 0;替换后效果如下:
| s1 | s2 | s3 | s4 | |
|---|---|---|---|---|
| h1 | 1 | 3 | 2 | 1 |
| h2 | 0 | 2 | 0 | 0 |
接着看第4行;S3值为1,h1=0, h2= 3,最终效果如下:
| s1 | s2 | s3 | s4 | |
|---|---|---|---|---|
| h1 | 1 | 3 | 0 | 1 |
| h2 | 0 | 2 | 0 | 0 |
这样,所有的行都被遍历一次了,最终得到的签名矩阵如下:
| s1 | s2 | s3 | s4 | |
|---|---|---|---|---|
| h1 | 1 | 3 | 0 | 1 |
| h2 | 0 | 2 | 0 | 0 |
基于这个签名矩阵,我们就可以估计原始集合之间的Jaccard相似度了。由于S1和S4对应的列向量完全一样,所以可以估计$SIM(S1,S4)=1$; 又比如说对于 S1和S3,两个元素中有一个一样,因此$SIM(S1,S3) = 0.5$
虽然用最小哈希签名矩阵可以近似估算两个集合的相似度,但是当哈希函数个数比较少的时候,估算误差可能会比较大,因此,需要选择恰当数量的哈希函数来降低估算误差。
局部敏感哈希
通过上面的方法处理过后,一篇文档可以用一个很小的签名矩阵来表示,节省下很多内存空间;但是,还有一个问题没有解决,那就是如果有很多篇文档,那么如果要找出相似度很高的文档,其中一种办法就是先计算出所有文档的签名矩阵,然后依次两两比较签名矩阵的相似度;这样做的缺点是当文档数量很多时,要比较的次数会非常大。那么我们可不可以只比较那些相似度可能会很高的文档,而直接忽略过那些相似度很低的文档。
因此接下来我们就讨论这个问题的解决方法——局部敏感哈希
首先,我们可以通过上面的方法得到一个签名矩阵,然后把这个矩阵划分成$b$个行条(band),每个行条由$r$行组成。
对于每个行条,存在一个哈希函数能够将行条中的每r个整数组成的列向量(行条中的每一列)映射到某个桶中。可以对所有行条使用相同的哈希函数,但是对于每个行条我们都使用一个独立的桶数组,因此即便是不同行条中的相同列向量,也不会被哈希到同一个桶中。
这样,只要两个集合在某个行条中有落在相同桶的两列,这两个集合就被认为可能相似度比较高,作为后续计算的候选对;
而那些在所有行条中都不落在同一个桶中的两列,就会被认为相似度不会很高,而被直接忽略。下面直接看一个例子:

可以看出,行条1中第2列和第4列的内容都为[0,2,1],所以这两列会落在行条1下的相同桶中,因此无论在剩下的3个行条中这两列是否有落在相同桶中,这两个集合都会成为候选对。在行条1中不相等的两列还有另外的3次机会成为候选对,因为他们只需在剩下的3个行条中有一次相等即可。
经过上面的处理后,我们就找出了相似度可能会很高的一些候选对,接下来我们只需对这些候选队进行比较就可以了,而直接忽略那些不是候选对的集合。这个方法适合用来计算相似度超过某个值的文档的相似度,而不适用于计算所有文档的相似度,因为那些相似度可能很低的文档已经被直接忽略了。
现在我们来定量分析一下:
假定将某个最小哈希签名矩阵划分为b组,每组有r行组成。此外,假定两个集合的Jaccard相似度为s。那么,两个集合被哈希到同一个桶中的概率与其Jaccard 相似度存在如下关系:
- 在具体某个组中,这对集合所有的最小哈希值都相等的概率是$s^r$
- 在这个组中,这对集合至少有一个位置的最小哈希值不相等的概率是$(1-s^r)$,即它们没有被映射到同一个桶中。
- 在任何一个组中,这对集合都没有被映射到同一个桶中的概率是$(1-s^r)^b$
- 进而,在整个最小哈希签名矩阵中,至少在一个组中的两个集合被映射到同一个桶中的概率为$1-(1-s^r)^b$
我们给定任意的r和b的值,以相似度s的值为横坐标,以概率$1-(1-s^r)^b$的概率为纵坐标,则在二维坐标系中展示了一条S曲线, 如下图所示:
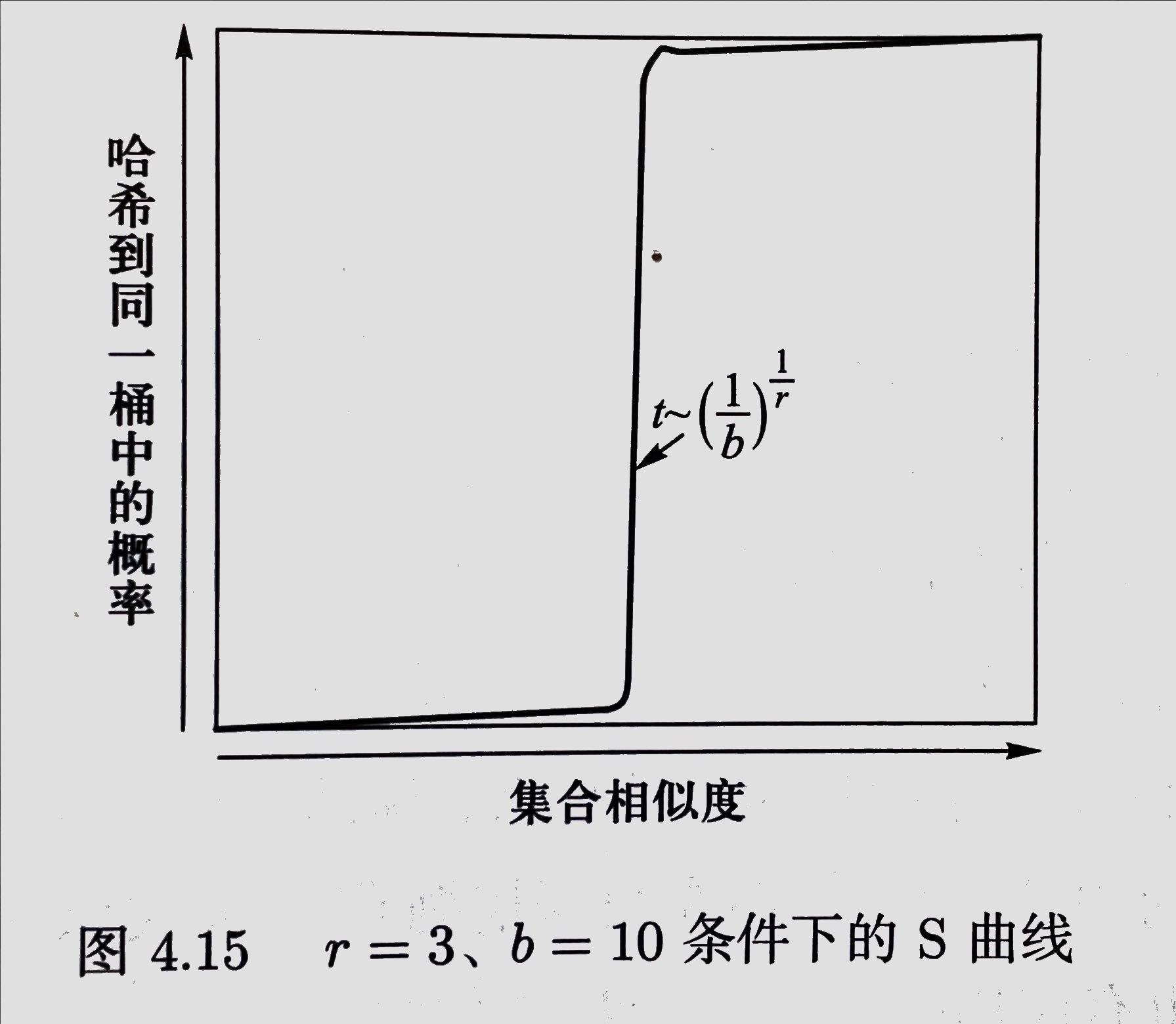
通常被映射到同一个桶中的概率的$\frac{1}{2}$处对应的s值被称为是相似度阈值。是一个关于b和r的函数。这一阈值的估计为$(1/b)^{1/r}$ 。对于较大的b和r,s值大于相似度阈值的几何对很有可能被哈希到同一个桶中,而小于相似度阈值的不太可能被哈希到同一个桶中。
例题
1
假设一个布隆过滤器的容量是 $8\times 10^9$ 位,集合中有 $1\times 10^9$ 个元素。如果使用3个哈希函数,试计算误判率。如果使用4个哈希函数,误判率如何?
- 当 $k=3$ 的时候
- 当$k=4$时候
2
假定全集A有n个元素,随机从中抽取出两个子集 $A_1,A_2$ ,且每个自己都有m 个元素,求$A_1$和$A_2$ 两个集合的期望相似度。
首先,我们写出两个子集 Jacorrd 相似度的表达式. 为我们令两者的交集大小为a
因此,我们可以计算期望
但是,我们要分情况讨论,因为 $m\leq \frac{n}{2}$ 和 $m>\frac{n}2$ 是不一样的