多重比较和双因子方差分析

之前我们学习了单因子方差分析，单因子方差分析是用来比较分组之间均值是否相等的问题，但是当我们拒绝原假设之后，我们不知道哪些组是相等的，哪些组是不相等的。因此我们需要进一步考虑这个问题。

多重比较

水平均值差的置信区间

首先我们要想，到底是原假设成立的时候，因子A是显著的还是备择假设成立的时候因子A是显著的。答案是备择假设，因为当原假设成立的时候，不同组之间的均值是相等的，因此因子A是不显著的。

当因子A显著时，有充分的理由认为因子A的各个水平中至少存在一对的均值是不相等的。但这并不说明，所有的水平均值都是不相等的。那么，我们就想知道哪些水平的均值是不相等的。一个很自然的想法就是，给定一对水平$(i,i’)$ ，构造$\mui-\mu{i’}$​ 的区间估计。如果该区间不包括0，就说明$\mui$和$\mu{i’}$必不相等。

我们来构造区间估计的枢轴量：

• 分布为：

$$\overline{y_{i\cdot}}\sim N(\mu_i,\frac{\sigma^2}{m})~ \text{和}~~\overline{y_{i'}}\sim N(\mu_{i'},\frac{\sigma^2}{m})$$

因为两者独立，所以 $\overline y{i\cdot}-\overline y{i’}\sim N(\mui-\mu{i’},2\sigma^2m^{-1})$​ . 对其进行标准化：

$$\frac{(\overline y_{i\cdot}-\overline y_{i'})-(\mu_i-\mu_{i'})}{\sqrt{2\sigma^2m^{-1}}}\sim N(0,1)$$

因为这个分布中$\sigma^2$是未知的，我们要用其估计 $\hat\sigma^2$来代替。估计哪里来呢？在两样本方差t检验中，定义的是和方差。那么在这个情况下，每一组都是对方差的一个估计，那么我们只要对每一组方差都进行一个加权平均就可以了。即$SS_E/n-a$ ，分母是由a个水平，每个水平是(m-1) 乘起来就是 $n-a$​​ 。 这样的估计更加稳定，因为有更多的组，波动更小。

多重比较问题

问题又来了，如果是两样本t检验的区间估计，只存在一个区间，但是在这个问题中,一共有a个不同的水平，总共有 a(a-1)/2 对不同的水平组合，每一对水平都有一个置信水平为1的置信区间。然而，要求其同时成立的话，其联合置信水平就无法达到$1-\alpha$了

比如说，若$A_1,A_2\cdots,A_k$ 表示k个随机事件，且每个事件发生的概率均为$1-\alpha$ ,即 $P(A_i)=1-\alpha.i=1,2\cdots,k$ 则其共同发生的概率为：

$$\begin{align} P(\cap_{i=1}^k A_i) &\leq P(A_1) = 1-\alpha\\ P(\cap_{i=1}^k A_i) &= 1-P(\cup_{i=1}^k\overline A_i)\\ &\geq 1-\sum_{i=1}^k P(\overline A_i) = 1-k(1-(1-\alpha))\\ &=1-k\alpha \end{align}$$

这说明它们同时发生的概率实际上要在$1-k\alpha$ 和 $1-\alpha$ 之间，可能要比 $1-\alpha$ 小很多

那么，为了使得它们同时发生的概率不低于$1-\alpha$ ，一个很自然的方法就是把每个事件发生的概率都提高。也就是让$\alpha$ 取得更小，让置信水平从 $1-\alpha/2$ 提高到 $1-\alpha/(a(a-1)/2)$

于是：

$$P(\cap_{i=1}^{a(a-1)/2}A_i) \geq 1-a(a-1)/2\cdot\frac{\alpha}{a(a-1)/2} = 1-\alpha$$

这叫做Bonferroni方法，虽然这种方法非常简单，但是会导致所得到的置信区间过于保守，精度很差

概述

在方差分析中，经F检验拒绝原假设，表明因子A是显著的，即a个水平的均值不全相等。进一步，我们需要确定哪些水平之间是存在差异的，哪些水平之间是没有差异的。

在$a(a>2)$ 个水平均值中同时比较任意两个水平均值间有无明显差异的问题叫做多重比较，也就是说，在显著性水平为 $\alpha$ 同时检验 $a(a-1)/2$ 个假设

$$H_0^{ii'}:\mu_i = \mu_{i'} .\\1\leq i<i'\leq a$$

当$H0^{ii’}$​ 成立时，$|\overline y{i\cdot}-\overline y_{i’}|$​ 不应过大，过大就应该拒绝 $H_0^{ii’}$​

于是，在同时考察这些 $H_0^{ii’}$ 时，这些$H_0^{ii’}$中至少有一个不成立就构成了多重比较检验的拒绝域，即拒绝域的形式就是：

$$W=\bigcup_{1\leq i<i'\leq a}\{|\overline y_{i\cdot}-\overline y_{i'\cdot}|\geq c_{ii'}\}$$

其中$c_{ii’}$是临界值，由原假设 $H_0^{ii’}$成立时$P(W)=\alpha$ 来确定。

Tukey方法

由多重比较我们可以得出，要求 $a(a-1)/2$​​​ 个临界值$c{ii’}$​​ 这是很烦的一件事， 而Tukey方法则对其进行了简化，对所求的临界值提出一些合理的假设。因为由于各个水平下重复次数均相等，基于对称性一个很自然的要求是$c{ii’}$​​是相等的，我们记为c。

$$P(W) = P(\bigcup_{i\leq i<i'\leq a}\{|\overline y_{i\cdot}-\overline y_{i'\cdot}|\geq c\})\\ =1-P(\bigcap_{1\leq i<i'\leq a}\{|\overline y_{i\cdot}-\overline y_{i'\cdot}|< c\})\\ =1-P(\max_{1\leq i<i'\leq a}\{|\overline y_{i\cdot}-\overline y_{i'\cdot}|< c\})\\ =P(\max_{1\leq i<i'\leq a}\{|\overline y_{i\cdot}-\overline y_{i'\cdot}|\geq c\})\\ =P(\max_{1\leq i<i'\leq a}|\frac{(\overline y_{i\cdot}-\mu)-(\overline y_{i'\cdot}-\mu)}{\hat\sigma/\sqrt m}|\geq \frac{c}{\hat\sigma/\sqrt m}\})\\ =P(\max_{i}\frac{(\overline y_{i\cdot}-\mu)}{\hat\sigma/\sqrt m}-\min_{i}\frac{\overline y_{i\cdot}-\mu}{\hat\sigma/\sqrt m}\geq \frac{c}{\hat\sigma/\sqrt m}\})\\$$

第一步就是 德摩根公式。

第二步：要求交集小于c，就是要让这里面最大的差值要小于c

第三步：正常转换

第四步：标准化，分子让其减去$\mu$和加上$\mu$,分母上除以$\hat\sigma/\sqrt m$

第五步：我们要求第四步式子的最大值，一定是最大减最小值。

我们要确定c的值，就要将c反解出来。

我们令不等号左边的式子为一随机变量：这是一个很复杂的随机变量，既有矩又有次序统计量。

$$q(a,df)=\max_{i}\frac{(\overline y_{i\cdot}-\mu)}{\hat\sigma/\sqrt m}-\min_{i}\frac{\overline y_{i\cdot}-\mu}{\hat\sigma/\sqrt m}$$

因为

$$\frac{\overline y_{i\cdot}-\mu}{\hat\sigma/\sqrt m}\sim t(n-a)$$

在原假设成立的情况下，$\mu_i$都为$\mu$

$q(a,df)$ 可以看做a个独立同分布的自由度为df的t分布的随机变量的极差。一般称q为t化极差统计量。

这个分布并不是常见的分布，它与水平数目a和t分布的自由度 df=n-a有关，但是与$\mu,\sigma^2,m$​ 无关。

概述

那么，如何获得t化极差统计量的分布？可以通过蒙特卡罗方法获得：

反解

我们可以由：

$$P(W) = P(q(a,df)\geq \sqrt m c/\hat\sigma) = \alpha$$

来推出：

$$c=q_{1-\alpha}(a,df)\hat\sigma/\sqrt m$$

其中，$q_\alpha(a,df)$表示$q(a,df)$的$\alpha$分位数

步骤

在给定的显著性水平$\alpha$下，确定t化极差统计量的分位数$q{1-\alpha}(a,df)$ 并计算 $c=q{1-\alpha}(a,df)\hat\sigma/\sqrt m$

比较每一组样本均值的差与临界值c的大小，如果$|\overline y{i\cdot}-\overline y{i’\cdot}\geq c$

那么认为水平i与水平 $i’$ 之间有显著差异，反之则认为这两个水平之间无差异

双因子方差分析

主效应与交互效应

事实上，在实际问题中，影响响应变量的因子数量不止一个，在这里我们考虑两个因子A和B。假定因子A有a个不同的水平，因子B有b个不同的水平，那么因子A和因子B的组合共有ab种。而且，在每一种因子组合下，对响应变量有m次重复观测。

当某一因子的水平改变时导致了响应变量发生变化，称该现象为因子效应。

某一因子对响应变量的直接影响，称为主效应

主效应

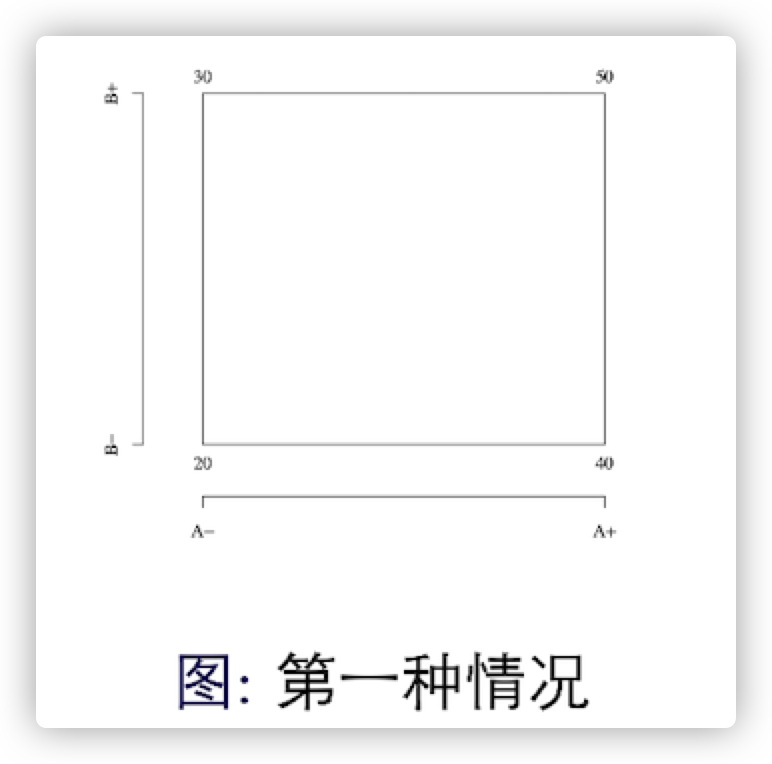
在这种情况下：

因子A的主效应： $= \frac{40+50}{2}-\frac{20+30}{2}=20$

因子B的主效应： $=\frac{30+50}{2}-\frac{20+40}{2}=10$​

这表明了：

因子A从低水平增至高水平时，其平均响应变量增加了20个单位

因子B从低水平增至高水平时，其平均响应变量增加了10个单位

交互效应

除了主效应之外，因子对响应变量的影响还存在另外一种形式：

• 在一些化工生产中，温度和材料都是影响产品质量的重要因素，不同材料在不同温度水平下对产品质量的影响是不同的
• 在线上购物行为中，消费者会存在从众心理，而线上商家会利用优惠券的让利形式进一步刺激消费者购买，因此在这些因素的共同作用下，电商主播直播带货非常火爆

所以说，当对于两个因子来说，因子A和因子B给响应变量产生的影响有影响，这种影响不是因子A对响应变量直接的影响，而是一种间接作用，称为交互效应。比如说这种情况：

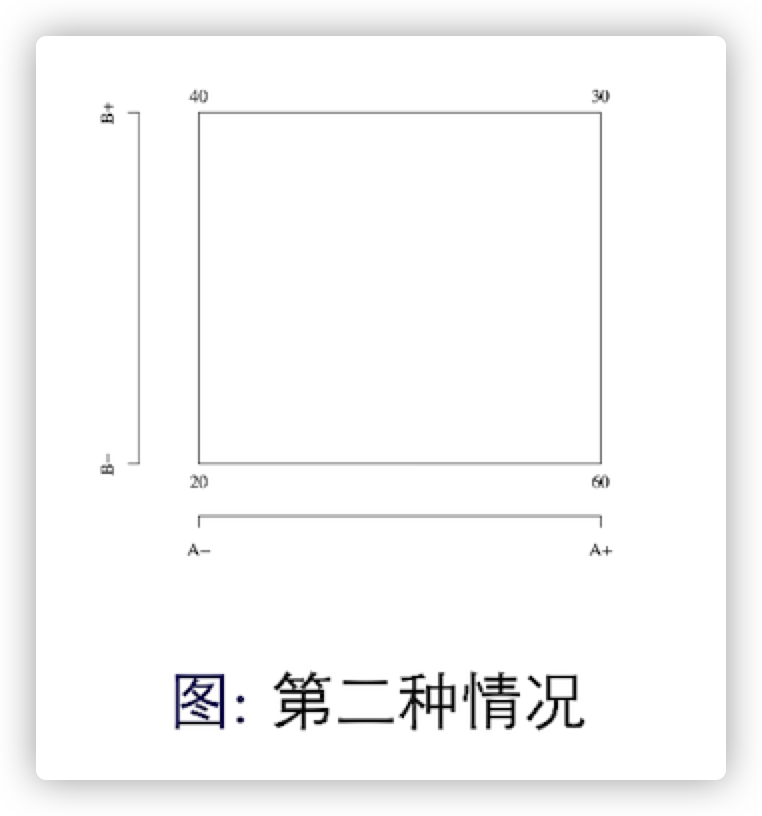
• 在因子B处于低水平时，因子A的效应为：$60-20=40$
• 在因子B处于高水平时，因子A的效应为：$30-40=-10$

这表明了，因子A的效应是依赖于因子B所选择的水平，由此可见因子A和因子B之间存在交互作用。交互作用的大小可以用因子B处于不同水平下因子A的效应的平均差来表示，即：

因子A和B的交互效应$=\frac{-10-40}{2}=-25$

判断方法

我们可以通过图像来判断两个因子之间是否存在交互效应：

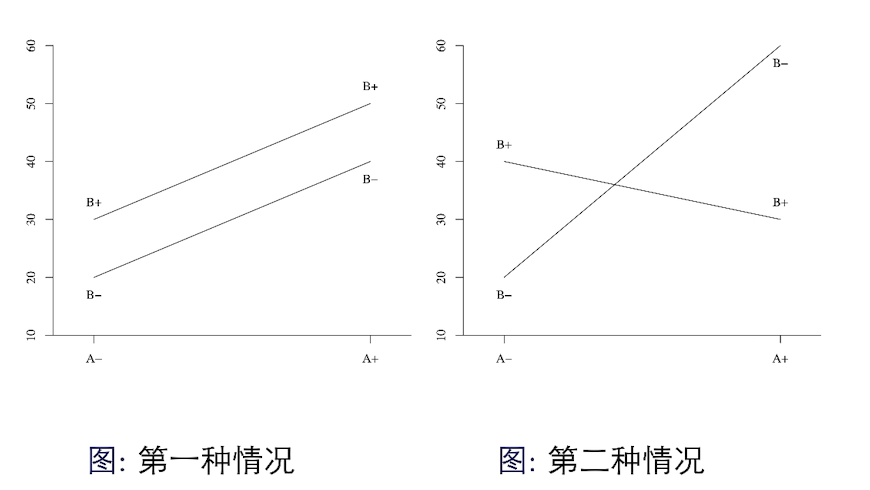
在第一种情况下，因子A无论在什么水平下，因子B的增量是一样的，因此可以判断A和B是不交互的

在第二种情况下，因子A的水平高低对B的增量产生影响，反之亦然，因此可以判断A和B是互相交互的。

双因子方差分析的模型及假设

那么我们有没有一个量化的方法来考虑这个问题呢？

首先，我们要给出一些假定：

• 因子A有a个水平，$i=1,2\cdots,a$

• 因子B有b个水平，$j=1,2\cdots,b$

• $y_{ijk}$​ 表示因子A处于第i个水平和因子B处于第j个水平时响应变量的第k个观测值，$k=1,2\cdots,m$

• 在这个模型中，样本量为$n=abm$

通常，数据按照下表的形式呈现：

和单因子方差分析的模型一样，双因子方差分析模型也有均值模型和效应模型

均值模型

在双因子方差分析的均值模型可以定义为：

$$y_{ijk} = \mu_{ij}+\epsilon_{ijk}\cases{i=1,2\cdots,a\\~\\j=1,2\cdots,b\\~\\k=1,2\cdots,m}$$

$\mu{ij}$可以认为是不同因子水平组合下响应变量$y{ijk}$的均值

效应模型

我们可以将$\mu_{ij}$分为四个部分，在双因子方差分析的效应模型可以定义为：

$$y_{ijk} = \mu+\alpha_i+\beta_j+(\alpha\beta)_{ij}+\epsilon_{ijk}\cases{i=1,2\cdots,a\\~\\j=1,2\cdots,b\\~\\k=1,2\cdots,m}$$

• $\mu$ 表示总体均值
• $\alpha_i$表示因子A(行因子)的第i个水平效应(主效应)
• $\beta_i$表示因子B(列因子)的第j个水平效应(主效应)
• $(\alpha\beta){ij}$表示因子A和B之间的交互关系，注意不等价于$\alpha_i\cdot\beta_j$ , 我们需要将$(\alpha\beta){ij}$​看成是一个新的符号？为什么不成立呢？因为一旦成立，交互效应就会等于主效应的乘积，那么就成为一个约束、一个假设了

此外，类似于单因子方差分析效应模型，为避免参数不可识别的问题，我们对这些效应参数需要一些约束

$$\begin{align} &\sum_{i=1}^a \alpha_i = 0,\\ &\sum_{j=1}^b\beta_j = 0,\\ &\sum_{i=1}^a(\alpha\beta)_{ij} = \sum_{j=1}^b (\alpha\beta)_{ij} = 0 \end{align}$$

此外我们要对实验误差$\varepsilon_{ijk}$ 进行一个假设，将其看成是均值为0且方差为$\sigma^2$ 的正态分布随机变量，即：

$$\varepsilon_{ijk} \sim N(0,\sigma^2)$$

总结

双因子方差分析模型的一般形式为：

$$\begin{align} &y_{ijk} = \mu+\alpha_i+\beta_j+(\alpha\beta)_{ij}+\varepsilon_{ijk},\varepsilon_{ijk}\sim N(0,\sigma^2)\\~\\ &i=1,2\cdots,a;j=1,2\cdots,b;k=1,2\cdots,m\\~\\ s.t.&\sum_{i=1}^a \alpha_i = 0,\sum_{j=1}^b \beta_i = 0\\ &\sum_{i=1}^a(\alpha\beta)_{ij}=\sum_{j=1}^b{(\alpha\beta)_{ij}}=0\ \end{align}$$

双因子方差分析的检验

检验问题

我们要检验的问题是：在双因子方差分析模型中，我们不仅关心因子A和B的主效应是否显著，还关心因子A和B的交互作用是否显著。

我们要针对以下三组问题进行检验

• 其一，判断因子A是否对响应变量有直接影响，即：

$$H_0:\alpha_1=\alpha_2\cdots=\alpha_a = 0~~vs~~H_1:\text{因子A至少存在一个水平}\alpha_i\neq 0$$

• 其二：判断因子B是否对响应变量有直接影响，即：

$$H_0:\beta_1=\beta_2=\cdots=\beta_b = 0 ~~vs~~H_1:\text{因子B至少存在一个水平}\beta_j\neq 0$$

• 其三，判断因子A和B是否对响应变量有交互作用，即：

$$\begin{align} &\text{H}_0 : \text{对于任意} i=1,2\cdots,a;j=1,2\cdots,b,(\alpha\beta)_{ij} = 0 ~~\text{均成立}\\~\\ &\text{H}_1: \text{因子A和B至少存在一组水平组合}(\alpha\beta)_{ij}\neq 0 \end{align}$$

检验统计量

我们采用方差分解的想法来构建检验统计量。在介绍总偏差平方和分解公式之前，我们先来定义写必需符号

• $y_{i\cdot\cdot}$ 表示在因子A第i个水平下响应变量的总和
• $y_{\cdot j\cdot}$ 表示在因子B第j个水平下响应变量的综合2
• $y_{ij\cdot}$ 表示在因子A第i个水平下且因子B第j个水平下响应变量的总和
• $y_{\cdots}$ 表示所有响应变量的总和
• $\overline y{i\cdot\cdot},\overline y{\cdot j\cdot},\overline y{ij\cdot},\overline y{\cdots}$ 表示相应的均值

我们可以用公式来表示这些符号，即：

$$\begin{align} &y_{i\cdot\cdot} =\sum_{j=1}^b\sum_{k=1}^m y_{ijk}&\overline y_{i\cdot\cdot}=\frac{1}{bm}y_{i\cdot\cdot}\\ &y_{\cdot j\cdot} = \sum_{i=1}^a\sum_{k=1}^m y_{ijk}&\overline y_{\cdot j\cdot} =\frac{1}{am} y_{\cdot j\cdot}\\ &y_{ij\cdot} = \sum_{k=1}^m y_{ijk}&\overline y_{ij\cdot} = \frac{1}{m}y_{ij\cdot}\\ &y_{\cdots} = \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^m y_{ijk} &\overline y_{\cdots} = \frac{1}{n}y_{\cdots} \end{align}$$

模仿单因子方差分析，我们可以给出$SS_T$的式子：

$$\begin{align} \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^m(y_{ijk}-\overline y_{\cdots})^2 &= \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^m((\overline y_{i\cdot\cdot}-\overline y_{\cdot\cdot\cdot})+(\overline y_{\cdot j\cdot}-\overline y_{ij\cdot})+(\overline y_{ij\cdot}-\overline y_{i\cdot\cdot}-\overline y_{\cdot j\cdot}+\overline y_{\cdot\cdot\cdot})+(\overline y_{ijk}-\overline y_{ij\cdot}))^2\\~\\ &=bm\sum_{i=1}^a (y_{i\cdot\cdot}-\overline y_{\cdot\cdot\cdot})^2+am\sum_{j=1}^b(\overline y_{\cdot j\cdot}-\overline y_{\cdot\cdot\cdot})^2+m\sum_{i=1}^a\sum_{j=1}^b(\overline y_{ij\cdot}-\overline y_{i\cdot\cdot}-\overline y_{\cdot j \cdot}+\overline y_{\cdot\cdot\cdot})^2+\sum_{i=1}^a\sum_{j-1}^b\sum_{k=1}^m(y_{ijk}-\overline y_{ij\cdot})^2 \end{align}$$

其中，中间项都是等于0的。用单因子的技巧就可以证明

• 注意到，第一项是根据因子A对数据进行划分从而引起的偏差平方和，我们记为$SS_A$
• 第二项类似地可以记为$SS_B$
• 第三项可以写为$m\sum{i=1}^a\sum{j=1}^b((\overline y{ij\cdot}-\overline y{\cdot\cdot\cdot})-(\overline y{i\cdot\cdot}-\overline y{\cdot\cdot\cdot})-(\overline y{\cdot j\cdot}-\overline y{\cdot\cdot\cdot}))^2$ , 记为 $SS_{AB}$
• 最后一项，为了排除因子A和B的效应之外响应变量的剩余偏差平方和，我们记为$SS_E$

总的偏差平方和的分解公式可以简记为：

$$SS_T = SS_A+SS_B+SS_{AB}+SS_E$$

类似于单因子方差分析模型，在双因子方差分析模型中，我们可以类似地利用三个比值：

$$\frac{SS_A}{SS_E},\frac{SS_B}{SS_E},\frac{SS_{AB}}{SS_E}$$

我们需要推导出$SSE$ 和在原假设成立时$SS_A,SS_B,SS{AB}$的分布

因为$SSA,SS_B,SS{AB},SSE$均为偏差平方和，所以一个合理的猜测是，这些偏差平方和的分布可能是一个卡方分布。根据Cochran定理，这些偏差平方和可以看做是多少个独立的随机变量的平方和。例如，$SS_A=bm\sum{i=1}^a(\overline y{i\cdot\cdot}-\overline y{\cdot\cdot\cdot})$ 可以将数据按因子A的a个水平来进行分组，在第i组内响应变量的均值$\overline y{i\cdot\cdot}$ 看作一个独立的样本，而$\overline y{\cdot\cdot\cdot}$​​可以看做a组数据的样本均值。

$SSA$​ 可以看做是这a个数据的离差平方和乘以一个常数。对于离差平方和来说，自由度可以看作样本个数减一。于是，$SS_A$​ 的自由度为a-1。类似地，我们可以得到$SS_B,SS{AB},SS_E$ 的自由度，如下表

类似于在单因子方差分析模型中的定义，偏差平方和除以相应的自由度之后所得到的被称为均方

其实，构造检验统计量实际上是均方的比值，而不是偏差平方和的比值，这是因为F分布随机变量的构造方式。根据之前的定理，我们发现 $MS_E$​​​ 一直在$\sigma^2$​​​ 附近波动。

只有当原假设成立时，$MSA,MS_B,MS{AB}$​​ 都会在$\sigma^2$​​ 附近波动的。于是，$\frac{MSA}{MS_E},\frac{MS_B}{MS_E},\frac{MS{AB}}{MS_E}$​​ 都应该比较接近于1的，并不会特别大。如果差得比较远，就说明某一效应非常明显，我们就会拒绝原假设。

因此，我们可以通过这三个比值，是否大于临界值，从而判断原假设成立，还是备择假设成立

均方的期望

在双因子方差模型中，均方$MSA,MS_B,MS{AB},MS_E$ 的期望分别为：

$$\begin{align} &E(MS_A)=E(\frac{SS_A}{a-1})=\sigma^2 +\frac{bm\sum_{i=1}^a \alpha_i^2}{a-1}\\ &E(MS_B)=E(\frac{SS_B}{b-1})=\sigma^2 +\frac{am\sum_{j=1}^b\beta_i^2}{b-1}\\ &E(MS_{AB})=E(\frac{SS_{AB}}{(a-1)(b-1)})=\sigma^2 +\frac{m\sum_{i=1}^a\sum_{j=1}^b(\alpha\beta)_{ij}^2}{(a-1)(b-1)}\\ &E(MS_E) = E(\frac{SS_E}{ab(m-1)})=\sigma^2 \end{align}$$

如何确定临界值？

当原假设成立的时候，类似单因子方差分析模型，我们可以推出

$$\begin{align} &SS_A\sim \mathcal{X}^2(a-1)\\ &SS_B\sim \mathcal{X}^2(b-1)\\ &SS_{AB}\sim \mathcal{X}^2((a-1)(b-1))\\ &SS_E\sim \mathcal{X}^2(ab(m-1)) \end{align}$$

而且$SSA,SS_B,SS{AB},SS_E$ 都是相互独立的

于是，一个显而易见的结论是我们所需要的比值都是服从F分布的，即

$$\begin{align} &\frac{MS_A}{MS_E}\sim F(a-1,ab(m-1))\\ &\frac{MS_B}{MS_E}\sim F(b-1,ab(m-1))\\ &\frac{MS_{AB}}{MS_E}\sim F((a-1)(b-1),ab(m-1))\\ \end{align}$$

由此，我们可以确定相应F分布的临界值