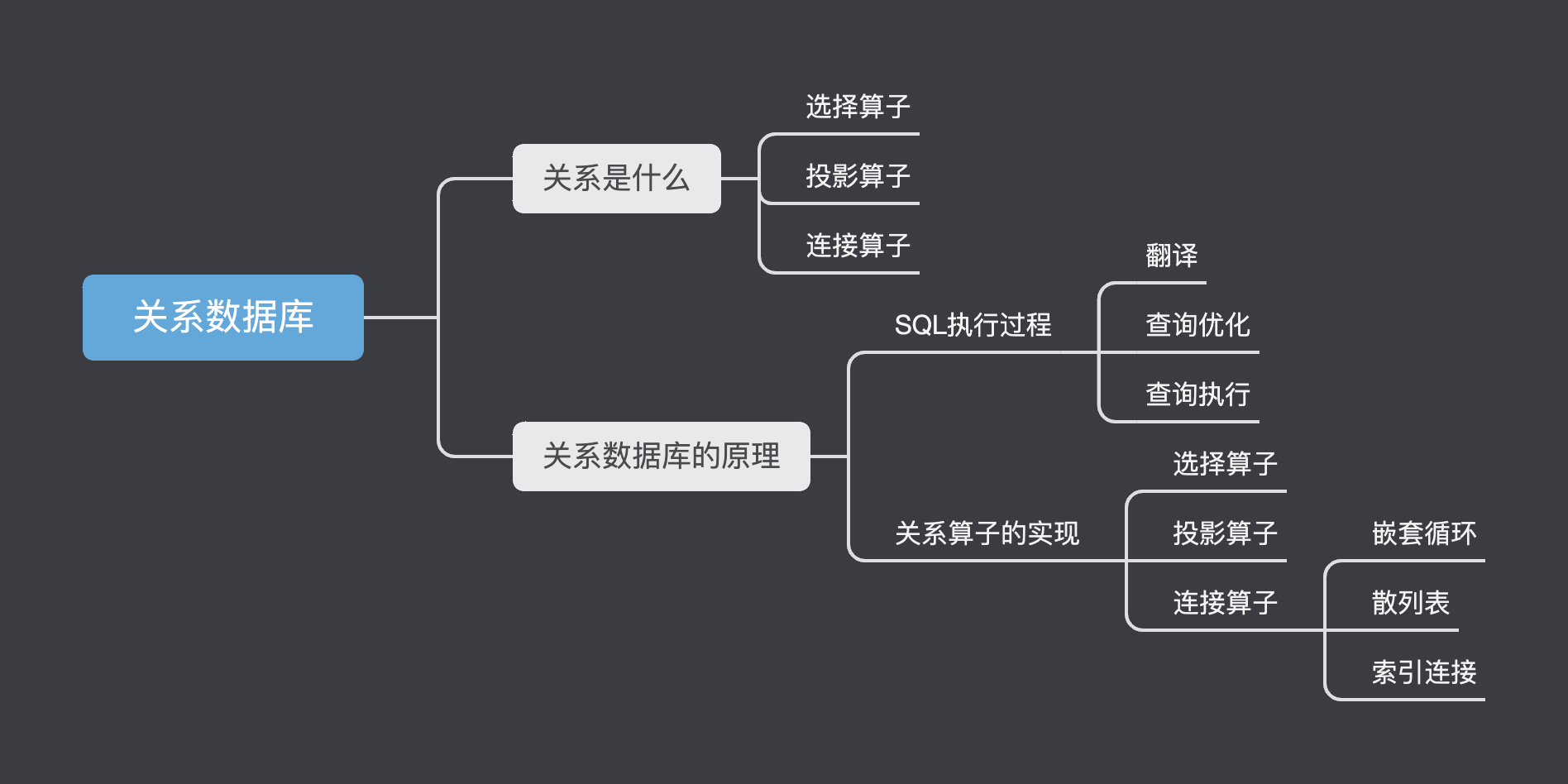
关系数据库及其基本实现原理

关系数据库

关系数据库简介

之前我们学了文档数据库，文档数据库更像是面向对象的一种表示模式。但是关系数据库用表格来存储数据，我们将表格的每一列看成是一个属性。

工程师们一开始并没有提出关系模型，一种叫做网状模型，一种叫做层次模型。在六十年代，IBM推出的IMS系统就是使用层次模型，GE推出的IDS使用的是网状模型

后来，Ted Codd提出了关系模型，其思想就是将数据管理系统从软件中解耦合出来形成一套独立的系统

网状模型问题

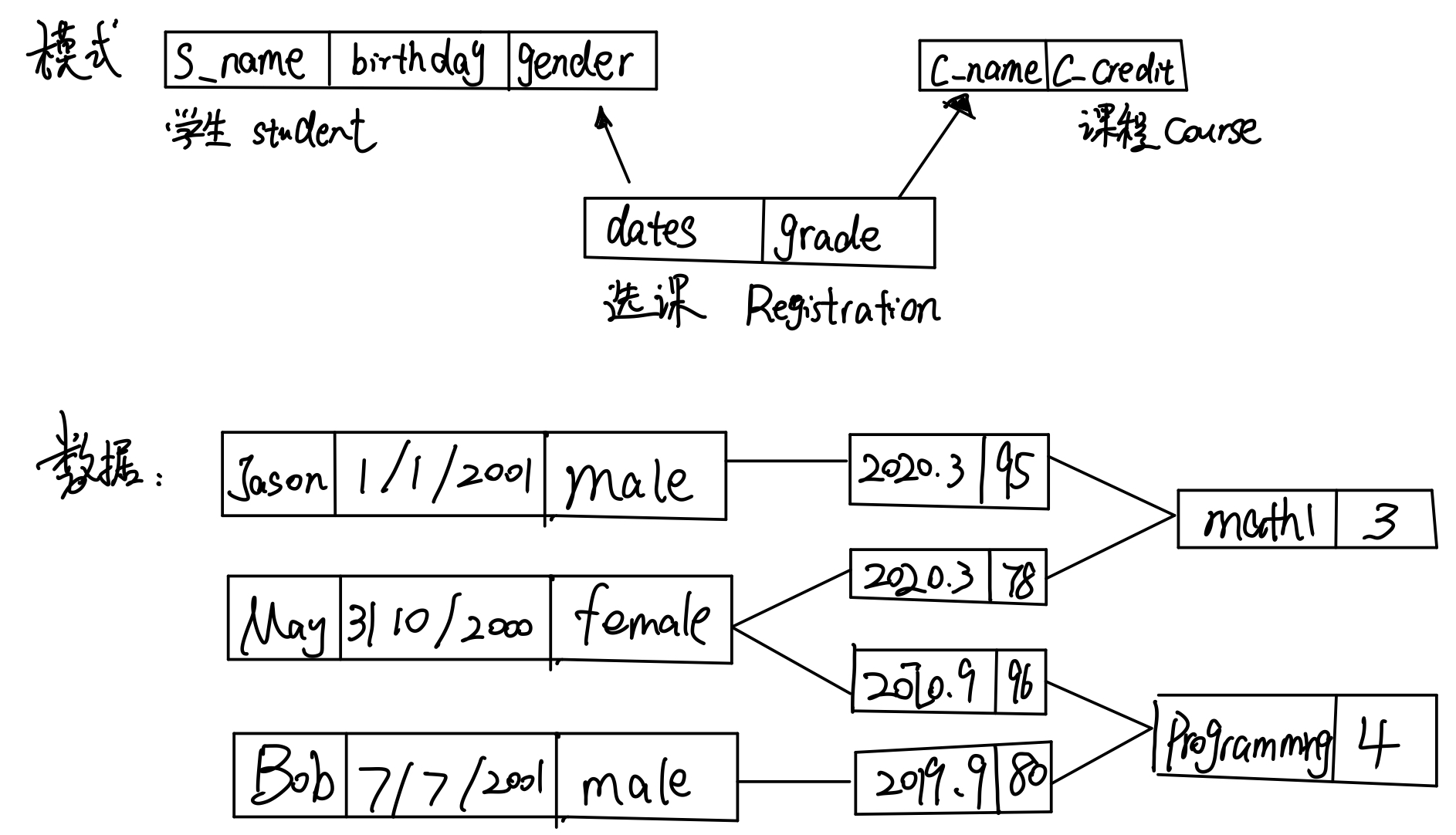
上图是网状数据结构的一个定义，在定义里有三个对象：学生、课程、选课。学生有三个属性，课程和选课各有两个属性。图下方的s数据就是根据上面的结构来存储的。

解决了数据存储的模式，程序员可以在程序中通过一些接口来访问数据库中的对象了。比如说：

-- 定义变量
student;course;registration;
-- 程序
Course.C_name = "math1";
find course using C_name;
while DB-status = 0 do
	get next Registration;
	get student;
	print Student.S_name;
	End;

• 用math1这个名称找到这门课
• 然后通过while循环，利用 get 来获取到每一个选择这门课的学生

我们发现要找到信息，完全是通过程序来实现的。但是Ted Codd认为，这样就让数据管理系统和应用系统之间的耦合度太高了，太复杂了。我们需要经常对数据机构和程序逻辑进行修改。他认为，这些查询的逻辑应该交给数据库自己做。因此他提出了关系型数据库。

关系数据库的构建思想

上面我们用程序实现了查找所有选择数学课的学生姓名，但这个程序时比较复杂的。能不能用很简单的方式来表达我们的需求呢？——谓词逻辑

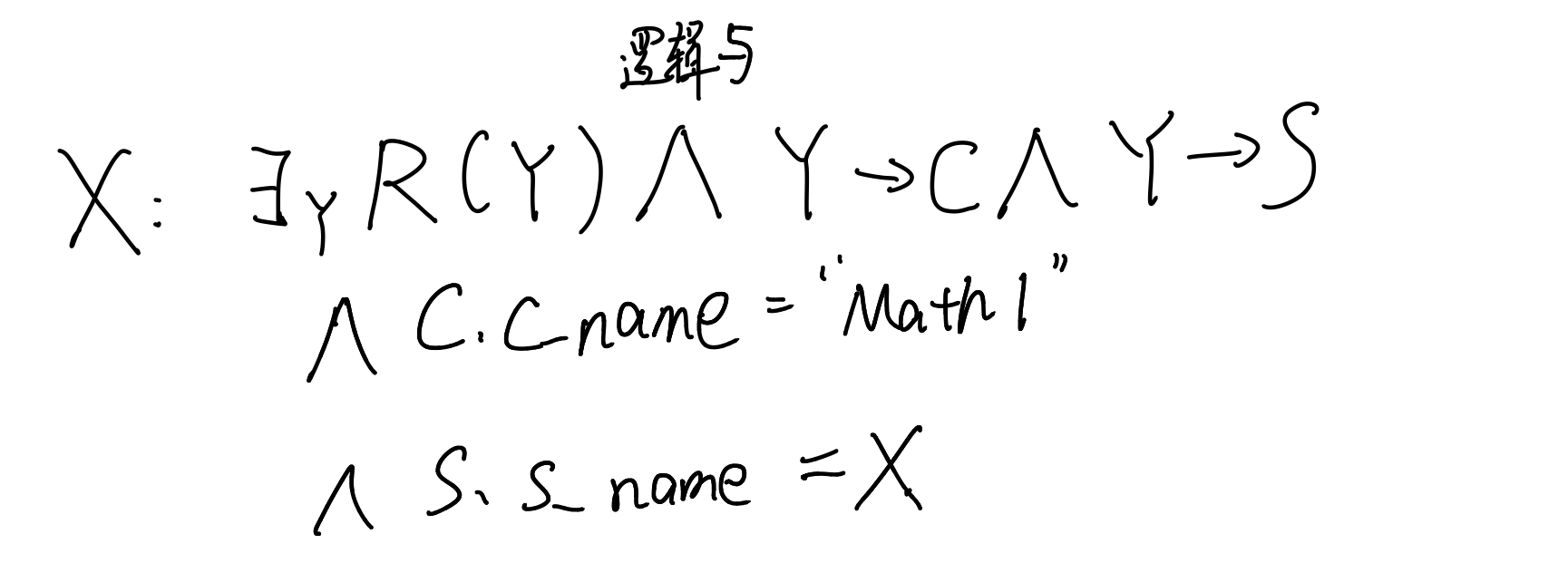
我们的需求可以用这样一段为此逻辑来表示。

存在这样一个选课的对象Y，这个选课对象和class有联系，和student也存在联系。并且，课程的名称为 “Math1”而学生的名字是X。我们要找的就是这个X

这是一种声明式的方式，相比于之前写的程序，这种方式更加简洁简单。对于怎么根据声明表达式来获得所需要的数据，交给数据库去处理。

但是并不是所有的逻辑表达式都可以被计算机以很高效的方式来处理，因此我们必须要考虑逻辑抽象的层次和表达能力的范围。Codd在这种谓词逻辑表达式中找到了一个子集，称为 Relational Calculus(关系演算) ，通过这种方式，计算机可以很快地理解我们的逻辑表达式。进而，这种模式演化成了关系数据库

关系模型

关系模型是将数据组织成表，这张表在关系模型中被称为关系。接下来我们给出一些定义：

• 域(domain)——> 集合(同一数据类型)，比如说{Jason,May,Bob}、{male,female}. 我们可以将其理解为数据库里某一属性的所有取值。有了域的概念，就可以来定义笛卡尔积
• 笛卡尔积：是数据的组合。从每个域中取出一个值形成一个集合，那么穷尽所有的集合就是这几个域的笛卡尔积。比如说对上面的两个域，其笛卡尔积中一共有 3X2 = 6 个组合。
• 有了上面的两个概念，我们可以定义关系(relation), 关系就是笛卡尔积的一个子集。子集中的组合可以构成一张表格，即关系

关系代数的概念

现在我们有三个关系，分别是student,course,sc 每一张表格的表头中存放的信息我们称之为属性 ，表中的每一行我们称之为元组。

现在我们要在这些关系上做计算，计算的方法叫做 关系代数(Relational Algebra) 。关系代数需要用到很多算子：

Operation	中文	符号	LATEXLATEX
Projection	投影	$\Pi$	\Pi
Selection	选择	$\sigma$	\sigma
Renaming	重命名	$\rho$	\rho
Aggregate Function	聚合函数	$\mathcal{G}$	\mathcal{G}
Union	交	$\cap$	\cap
Intersection	补	$\cup$	\cup
Natural Join	自然连接	$\bowtie$	\bowtie
Left Outer Join	左外连接	⟕	… 这几个直接复制吧
Right Outer Join	右外连接	⟖
Full Outer Join	全外连接	⟗
Cartesian product	笛卡尔乘积	$\times$	\times
Divide	除	$\div$	\div
Assignment	赋值	$\leftarrow$	\leftarrow
And	条件并列	$\land$	\land or \vee
Negation	非	$\neq$	\neg
Exist	存在	$\exists$	\exists
For All	对所有	$\forall$	\forall

选择操作

首先我们关注选择算子，用小写的$\sigma$ 来表示。它可以通过计算，将一个关系变为另一个关系。其使用方式如下：

$$\sigma_A(R)$$

R 代表要选择的关系

A代表选择的条件

计算的结果就是一个包含了所有在R里面且符合A条件的元组的关系

比如说：$\sigma_{\text{s.name=’Jason’}}(\text{Student})$​​ 最后得到的结果就是 $(S001,Jason,1/1/2001,male)$​。就是在Student关系中选择名字为‘Jason’的元组。

投影操作

投影我们用$\Pi$​​来表示，起作用是对一个关系进行纵向的切分，将一些属性剔除并返回一个关系。其参数和选择算子是一样的：

$$\Pi_A(R)$$

A 代表属性的一个集合

R 代表要投影的关系

值得注意的是，当切分结束的时候，可能会得到 重复的元组，因此在投影结束之后还需要去重

连接操作

连接和选择、投影是不一样的，连接是一个二元算子，也就是需要两个关系。用法如下：

$$S \bowtie_A R$$

S，R代表两个关系

A 代表连接条件

其操作逻辑就是将S和R先做一个笛卡尔积，再在其基础上做一个条件为A的选择，也就是 $S \bowtie_A R=\sigma_A(S\times R)$

比如说：

$$\text{Student}\bowtie_{\text{student.sno = sc.sno}}\text{SC}$$

这里，$\text{student.sno=sc.sno}$ 称之为等值连接

关系代数表达式

现在，我们想要所有选了Math1这门课的学生的名字，怎么用关系代数表达式来表述呢？

我们需要将Course和SC进行一个连接，这样就能知道学生的学号了。

$$\Pi_{\text{student.sname}}(\text{Student}~~~~~\overset\bowtie{\text{student.sno=sc.sno}}~~~~(\text{SC}~~~~ \overset\bowtie{\text{sc.cno=course.cno}}~~~~~~ \sigma_{\text{cname="math1"} }(\text{Course})))\\$$

首先，在Course关系里面选择课程名称为math1的课，和SC关系做连接，连接条件为cno相等。接着，连接Student关系，连接条件为sno相等。最后做一个投影，投影条件是学生名字

基于这样的关系表达式，工程师开发了SQL语言。

例题

假设学校的教务系统里有三张表：学生表(学号，姓名，生日，性别，学院)、课程表(课程号，课程名称，学分，主讲老师)、选课表(学号，课程号，学期，成绩)。其中，学生表记录了10万个学生的信息，课程表记录了2000门课的信息，选课表中有200万条选课记录。假设我们在学生表的”学号”、课程表的“课程号”、选课表的“学号”和“课程号”上分别创建了四个索引，其余的属性上都没有索引。以下三个关系代数表达式的目的都是查询“所有在张三老师的课上成绩超过90分的学号和姓名”

$$a.~\Pi_{\text{学号,姓名}}(\text{学生表}\bowtie(\sigma_{\text{成绩}>90}(选课表)\bowtie\sigma_{\text{主讲老师='张三'}}(课程表)))\\ b.~\Pi_{\text{学号,姓名}}(\text{学生表}\bowtie\Pi_{学号}(\sigma_{成绩>90\and\text{主讲老师='张三'}}){(\text{选课表}\bowtie\text{课程表})})\\ c.~\Pi_{\text{学号,姓名}}(\text{学生表}\bowtie(\sigma_{\text{成绩>90}}(\text{选课表}\bowtie\sigma_{\text{主讲老师='张三'}}(课程表))))$$

上面三种方法，那种执行方法最好？

答案是：C.

因为选课表有200万张，对于a来说，$\sigma_{\text{成绩>90}}(选课表)$的范围太大了，可能会导致效率很拉跨。
对于b，$\text{选课表}\bowtie\text{课程表}$ 需要选课表和课程表做一个笛卡尔积，这边没有任何条件，因此要做一个200万*2000的笛卡尔积，非常慢

对于c，我们现从选课表中找到主讲老师为张三的课程号，这些课程是很少的。而且在课程号上有索引，因此查询会比较快。在做笛卡尔积的时候会减少很多的量，然后再去筛选成绩大于90的同学。

关系数据库的基本实现原理

关系数据库的基本架构

我们知道，sql语言是声明式语言。我们告诉数据库系统我们想要什么，数据库会通过内置的算法帮我们找到。这类似于一个黑箱操作，我们学会了sql语言但却并不了解数据库中的原理，那么现在我们就来学习一下其中的操作。

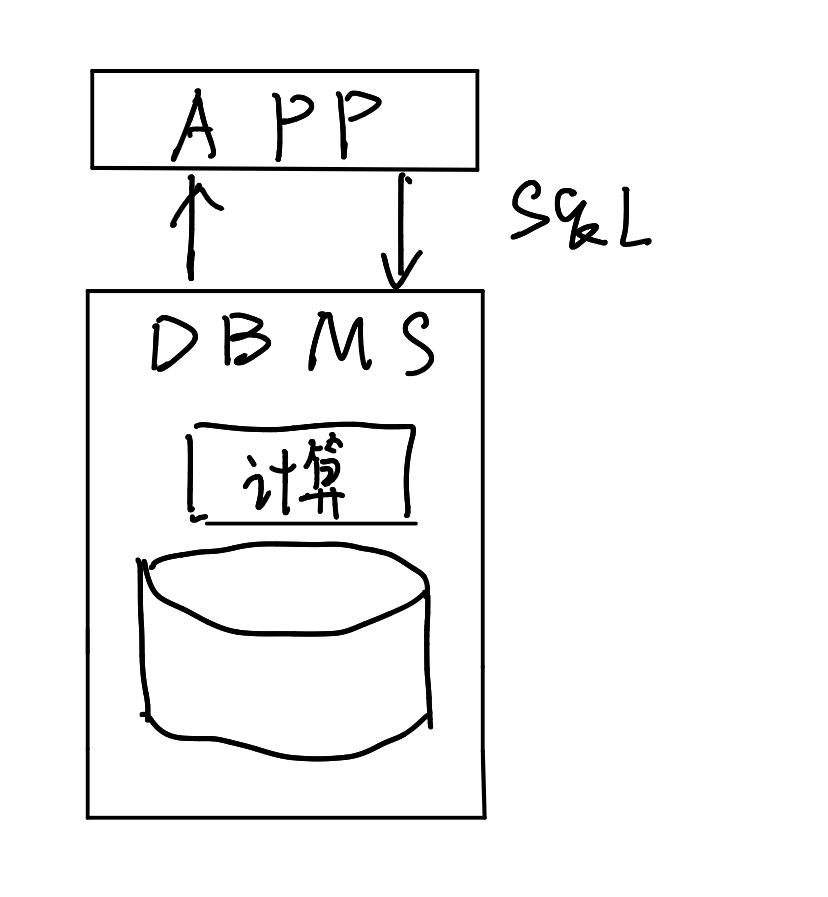
现在我们通过上面这张图来介绍一下查询的流程。首先，应用将SQL查询提交给DBMS。接着系统要从存储层获取数据到计算层，计算完成后将结果返还给APP。因为SQL语言还是比较直白的，因此在获取了数据之后，计算层需要通过复杂的计算才能获得结果。

首先我们看存储层，关系型数据库是怎么存储的呢？首先，关系是由一张一张表构成的，而我们知道数据库里需要用页来存储才能有效利用空间。于是，我们需要对表进行分页处理，每页里面存放着若干元组，通过若干页面将整张表的信息存储下来，最后通过一个结构(表头)将所有页存储下来(可以是索引、inode):

解决了存放的方式之后，我们可以对数据进行很简单的访问，比如说对数据表进行整体的扫描，对是否称为sql查询的结果进行比对。但是通过扫描或者索引的访问，并不能完成整个sql的查询，因此在计算层需要进行相对复杂的计算

SQL查询的执行过程

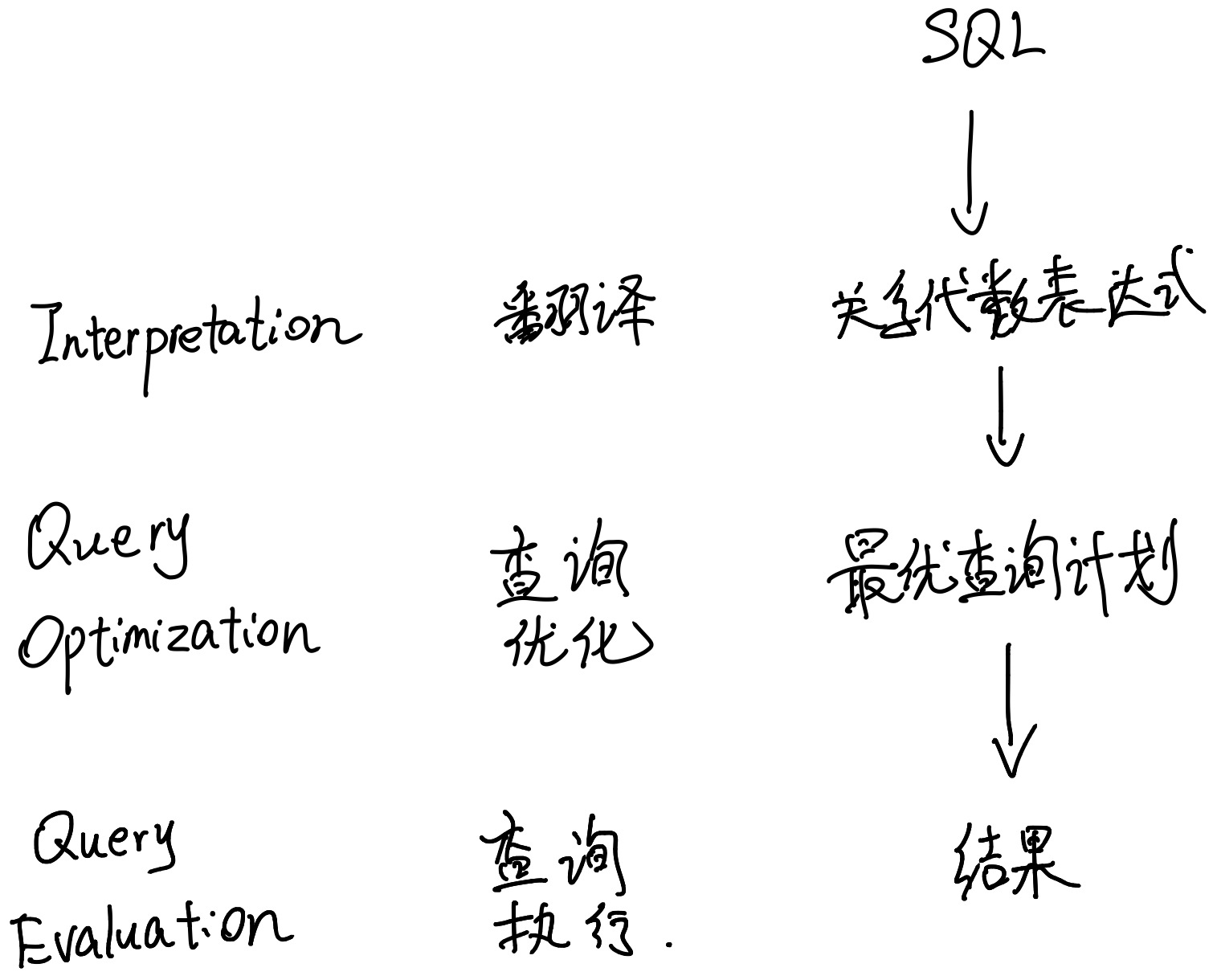
翻译

首先，要将SQL语句翻译成关系代数表达式。

比如说有这么一段简单的sql语句：

SELECT sname
FROM student,sc
WHERE student.sno = sc.sno
AND sc.grade < 60

经过翻译，可以将其变成不同形态的关系代数表达式

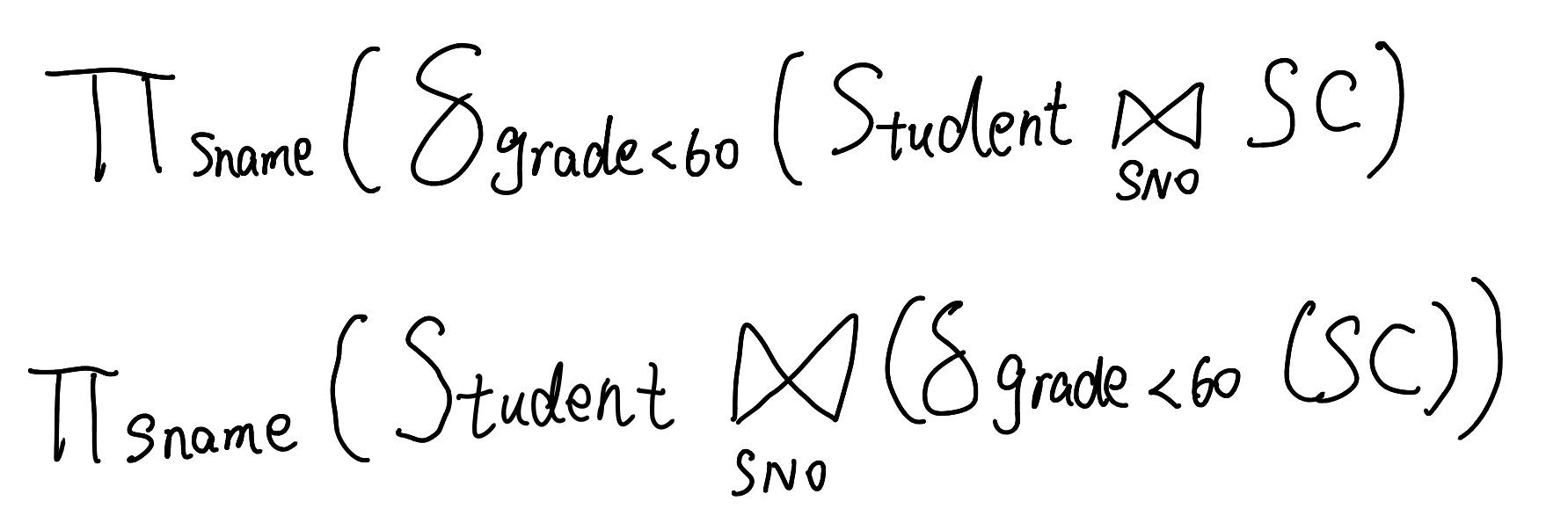
他们的执行步骤可能是不一样的，但是执行的结果确实相同的。比如说第一条关系代数表达式。首先让Student、SC两张表通过SNO进行等值连接，形成一张大表；然后在表里面做选择，选择成绩小于60分的信息；最后在名字这个属性上进行一个投影，最后得到我们想要的结果。

因此，关系表达式确定了一段sql语句在数据库里应该做什么。但是就如上面生成的两条关系代数表达式，如果一段sql非常复杂，他可能生成不计其数的关系代数表达式，那么这时候我们需要做的就是在这里面选择查询效率最高的表达式来执行。

查询优化

在查询优化这一步，计算机做的更多是一种预测，预计哪一种查询计划最有效。因此在这一步需要一些AI来选择最优解

查询执行

接下来我们要讲的几节就关注于查询执行。我们要学习每种算子在计算层中是如何实现的。

数据处理的性能问题

因为数据绝大部分都是存储在DISK上的，而硬盘和内存之间的交互时间非常长，因此在数据密集型计算中，cpu 长时间处于空闲状态，在等待内存和硬盘之间的I/O交互。因此我们用 I/O 次数来衡量数据处理的性能，一个好的算法约等于 I/O次数低的算法

选择算子的实现

接下来我们来看选择算子的实现。我们知道数据库是将表存放在多个页里面的，然后通过一个结构来把所有页联系起来；此外我们还可以用索引的方式将页给联系起来。

访问一张表，我们可以采用两种方式：

• 扫描/Scan
• 索引访问 / Index Access

比如说我要进行一个 SELECT * FROM R WHERE A= 100

情况如下：采用结构存储的形式，需要在结构中存放100页的地址；采用索引查找的方式有三层索引；

如果使用索引访问，且刚好A是索引，那么我们需要访问4个页面，4次I/O才能访问到单独的页

如果使用扫描的方法，需要100次I/O才能找到。

当满足选择条件的元组特别多的话，那么I/O开销会更加大。

投影算子的实现

比如说做完 $\Pi_{\text{major}}(R)$​​​​ 投影之后，关系剩下 {(CS),(Math),(CS)} 这三个元组, 我们需要考虑去重。

对于乱序的遗传数据，直接去重是比较复杂的，因此我们可以对其先进行一次排序，然后再去重就比较容易了。因此如何高效率得排序就成了最关键的问题。当然可以使用快排的东西，但是数据量大的话没有办法将其全部存放到内存里面，我们的想法是增强数据访问的局部性来降低 I/O 操作的次数。因此这里介绍外部排序

对于25212245434215213 这一串数据，假设它无法全部放到内存中，一次只能调入6个，那么首先要对其进行局部排序。

• 从磁盘读取252122 ，进行排序，122225，然后写回到硬盘上
• 从磁盘中读取454342，进行排序，234445，写回
• 从磁盘中读取15213，进行排序，11235，写回

对每次写回的数据的头部插入一个指针，然后进行归并操作(类似于归并排序)。最后需要写入硬盘中

通过这种方式，可以大大减少I/O的次数，虽然计算的次数比较多，但是在数据密集型计算中，减少I/O次数节省的时间要远远多于增加计算次数所花费的时间

连接算子的实现

嵌套循环

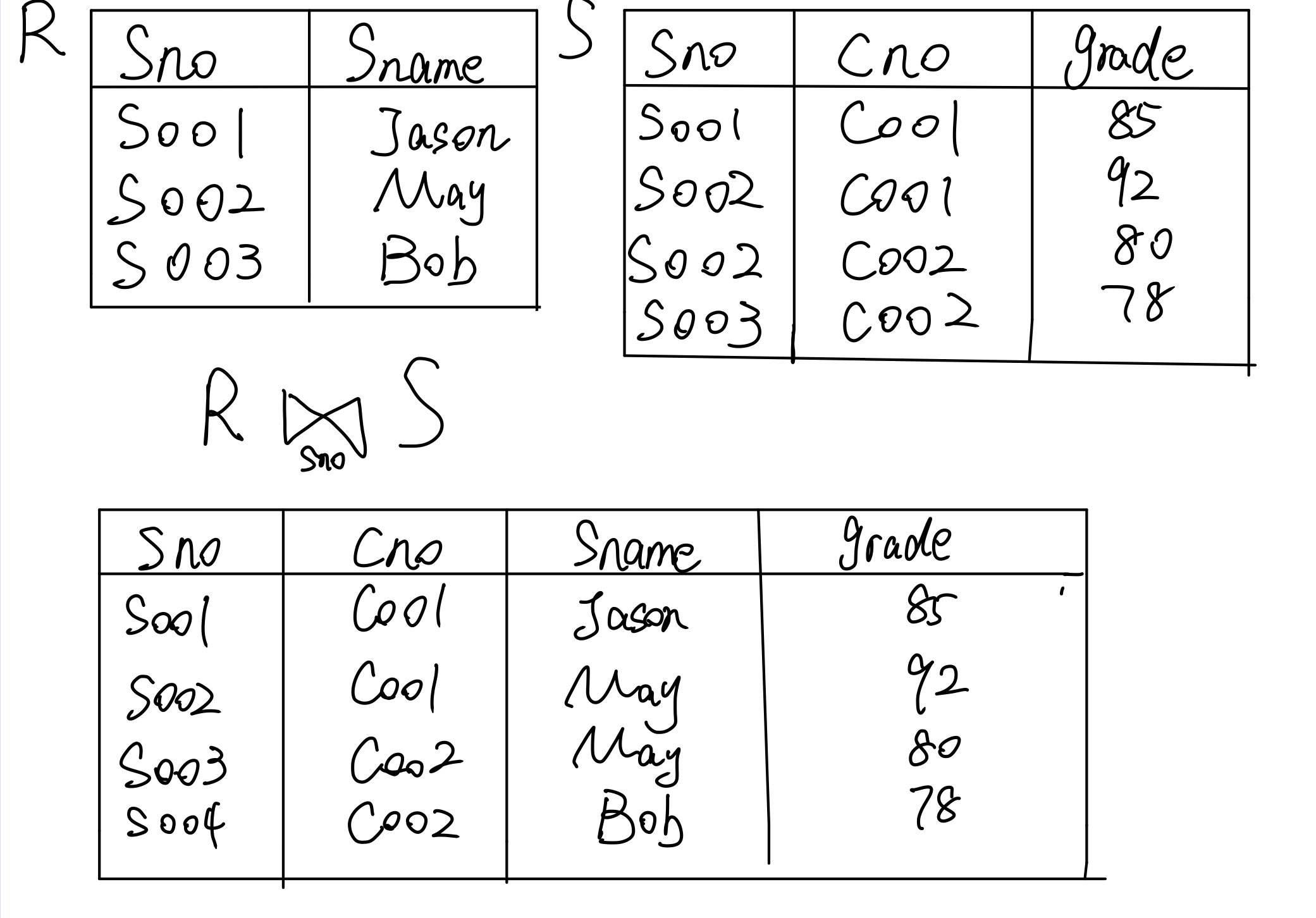
现在我们来介绍一下嵌套循环的实现。假设有两个关系R和S，我们对其进行 sno相等的连接操作，那么很朴素的一种想法是做一个双重循环，R中的每一个Sno和 S中的 Sno一一比对，如果匹配上了，就将其连接起来，放到新关系中去。用简单的逻辑表达式，可以这样写：

$$\text{For r in R:}\\ ~~~~~~~~~~~ \text{For s in S:}\\ ~~~~~~~~~~~~~~~~~~~~~~ \text{if(r }\bowtie ~\text{s)}\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \text{output r}\cdot \text{s}$$

我们可以采取另一种策略，就是将R中的n个元组拿出来和S表进行扫描。我们可以把磁盘中的R中的M个元组放到内存里去，然后用S和M个元组一起作比较。在这种情况下需要 $|R|\times B(S)$​

这时候，逻辑如下：

For M in R
	For s in S
		if(M \bowtie s)
			output ...

这时候可以有效减少 I/O 的次数

即： $B(R)/M \cdot B(S)$

适用于查询的选择性强、约束性高并且仅返回小部分记录的结果集。通常要求 外表的记录（符合条件的记录，通常通过高效的索引访问） 较少，且 内表连接列有唯一索引或者选择性强的非唯一索引时，嵌套循环连接的效率是比较高的。

MYSQL中的嵌套连接

在Mysql中使用Join，有很多规矩：比如两表 join 要小表驱动大表，阿里开发者规范禁止三张表以上的 join 操作

Nested Loop Join 是扫描驱动表，每读出一条记录，就根据 join 的关联字段上的索引去被驱动表中查询对应数据。它适用于被连接的数据子集较小的场景，它也是 MySQL join 的唯一算法实现，关于它的细节我们接下来会详细讲解。

MySQL 中有两个 Nested Loop Join 算法的变种，分别是 Index Nested-Loop Join 和 Block Nested-Loop Join(接近于Hash Join)。

Index Nested-Loop Join 算法

下面，我们先来初始化一下相关的表结构和数据

CREATE TABLE `t1` (
  `id` int(11) NOT NULL,
  `a` int(11) DEFAULT NULL,
  `b` int(11) DEFAULT NULL,
  PRIMARY KEY (`id`),
  KEY `a` (`a`)
) ENGINE=InnoDB;

delimiter ;;
# 定义存储过程来初始化t1
create procedure init_data()
begin
  declare i int;
  set i=1;
  while(i<=10000)do
    insert into t1 values(i, i, i);
    set i=i+1;
  end while;
end;;
delimiter ;
# 调用存储过来来初始化t1
call init_data();
# 创建并初始化t2
create table t2 like t1;
insert into t2 (select * from t1 where id<=500)

有上述命令可知，这两个表都有一个主键索引 id 和一个索引 a，字段 b 上无索引。存储过程 init_data 往表 t1 里插入了 10000 行数据，在表 t2 里插入的是 500 行数据。

为了避免 MySQL 优化器会自行选择表作为驱动表，影响分析 SQL 语句的执行过程，我们直接使用 straight_join 来让 MySQL 使用固定的连接表顺序进行查询，如下语句中，t2是驱动表(较小)，t1是被驱动表(较大)。

select * from t2 straight_join t1 on (t2.a=t1.a);

我们看到，t1表上的a字段是有一个索引的，Join过程中使用了该索引，因此SQL语句得执行流程如下：

• 从t2表中读取一行数据L1
• 使用L1的a字段，去t1表中作为条件进行查询，此时会用到索引查询
• 取出t1中满足条件的行，跟L1组成相应的行，成为结果集的一部分
• 重复执行，直到扫描完t2表

这个流程我们就称之为 Index Nested-Loop Join，简称 NLJ，它对应的流程图如下所示。

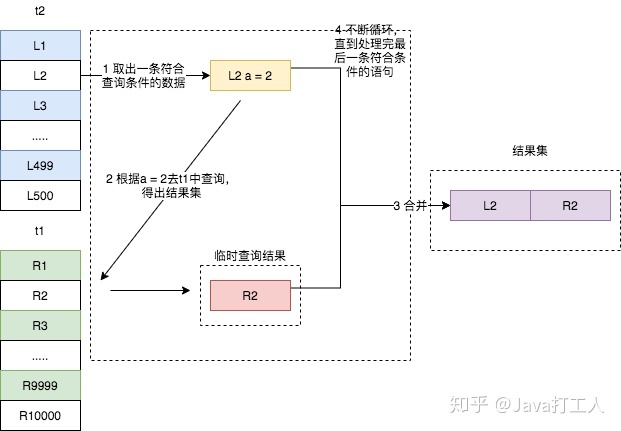
需要注意的是，在第二步中，根据 a 字段去表t1中查询时，使用了索引，所以每次扫描只会扫描一行(从explain结果得出，根据不同的案例场景而变化)。

假设驱动表的行数是N(这里是500)，被驱动表的行数是 M(这里是10000)。因为在这个 join 语句执行过程中，驱动表是走全表扫描(Explain中显示为ALL)，而被驱动表则使用了索引，并且驱动表中的每一行数据都要去被驱动表中进行索引查询，所以整个 join 过程的近似复杂度是 $O(N\log_2M)$。显然，N 对扫描行数的影响更大，因此这种情况下应该让小表来做驱动表(外表)。

当然，这一切的前提是 join 的关联字段是 a，并且 t1 表的 a 字段上有索引。

如果没有索引时，再用上图的执行流程时，每次到 t1 去匹配的时候，就要做一次全表扫描。这也导致整个过程的时间复杂度变成了 $O(N * M)$，这是不可接受的。所以，当没有索引时，MySQL 使用 Block Nested-Loop Join 算法。

Block Nested-Loop Join 算法

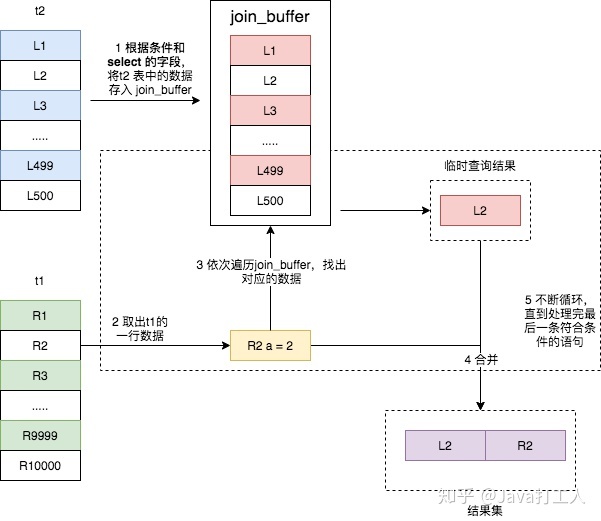
Block Nested-Loop Join的算法，简称 BNL，它是 MySQL 在被驱动表上无可用索引时使用的 join 算法，其具体流程如下所示：

• 把表 t2 的数据读取当前线程的 join_buffer 中，在本篇文章的示例 SQL 没有在 t2 上做任何条件过滤，所以就是讲 t2 整张表 放入内存中；
• 扫描表 t1，每取出一行数据，就跟 join_buffer 中的数据进行对比，满足 join 条件的，则放入结果集。

比如下面这条 SQL

select * from t2 straight_join t1 on (t2.b=t1.b);

这条语句的 explain 结果如下所示。可以看出

可以看出，这次 join 过程对 t1 和 t2 都做了一次全表扫描，并且将表 t2 中的 500 条数据全部放入内存 join_buffer 中，并且对于表 t1 中的每一行数据，都要去 join_buffer 中遍历一遍，都要做 500 次对比，所以一共要进行 500 * 10000 次内存对比操作，具体流程如下图所示。

主要注意的是，第一步中，并不是将表 t2 中的所有数据都放入 join_buffer，而是根据具体的 SQL 语句，而放入不同行的数据和不同的字段。比如下面这条 join 语句则只会将表 t2 中符合 b >= 100 的数据的 b 字段存入 join_buffer。

select t2.b,t1.b from t2 straight_join t1 on (t2.b=t1.b) where t2.b >= 100;

join_buffer 并不是无限大的，由 join_buffer_size 控制，默认值为 256K。当要存入的数据过大时，就只有分段存储了，整个执行过程就变成了：

• 扫描表 t2，将符合条件的数据行存入 join_buffer，因为其大小有限，存到100行时满了，则执行第二步；
• 扫描表 t1，每取出一行数据，就跟 join_buffer 中的数据进行对比，满足 join 条件的，则放入结果集；
• 清空 join_buffer；
• 再次执行第一步，直到全部数据被扫描完，由于 t2 表中有 500行数据，所以一共重复了 5次

这个流程体现了该算法名称中 Block 的由来，分块去执行 join 操作。因为表 t2 的数据被分成了 5 次存入 join_buffer，导致表 t1 要被全表扫描 5次。

	全部存入	分5次存入
内存操作	10000*500	10000*(100+100+100+100+100)
扫描行数	10000+500	10000*5+500

如上所示，和表数据可以全部存入 join_buffer 相比，内存判断的次数没有变化，都是两张表行数的乘积，也就是 10000 * 500，但是被驱动表会被多次扫描，每多存入一次，被驱动表就要扫描一遍，影响了最终的执行效率。

基于上述两种算法，我们可以得出下面的结论，这也是网上大多数对 MySQL join 语句的规范。

• 被驱动表上有索引，也就是可以使用Index Nested-Loop Join 算法时，可以使用 join 操作。
• 无论是Index Nested-Loop Join 算法或者 Block Nested-Loop Join 都要使用小表做驱动表。

因为上述两个 join 算法的时间复杂度至少也和涉及表的行数成一阶关系，并且要花费大量的内存空间，所以阿里开发者规范所说的严格禁止三张表以上的 join 操作也是可以理解的了。

但是上述这两个算法只是 join 的算法之一，还有更加高效的 join 算法，比如 Hash Join 和 Sorted Merged join。可惜这两个算法 MySQL 的主流版本中目前都不提供，而 Oracle ，PostgreSQL 和 Spark 则都支持，这也是网上吐槽 MySQL 弱爆了的原因(MySQL 8.0 版本支持了 Hash join，但是8.0目前还不是主流版本)。

其实阿里开发者规范也是在从 Oracle 迁移到 MySQL 时，因为 MySQL 的 join 操作性能太差而定下的禁止三张表以上的 join 操作规定的 。

散列连接

散列连接(Hash Join)的实现思路不太一样。其实现逻辑如下：

现在有两张表 R和S，我们对R进行一次扫描，通过哈希函数$H(x)$将里面的元组放到k个桶里。然后对S进行相同的操作，结果如下：

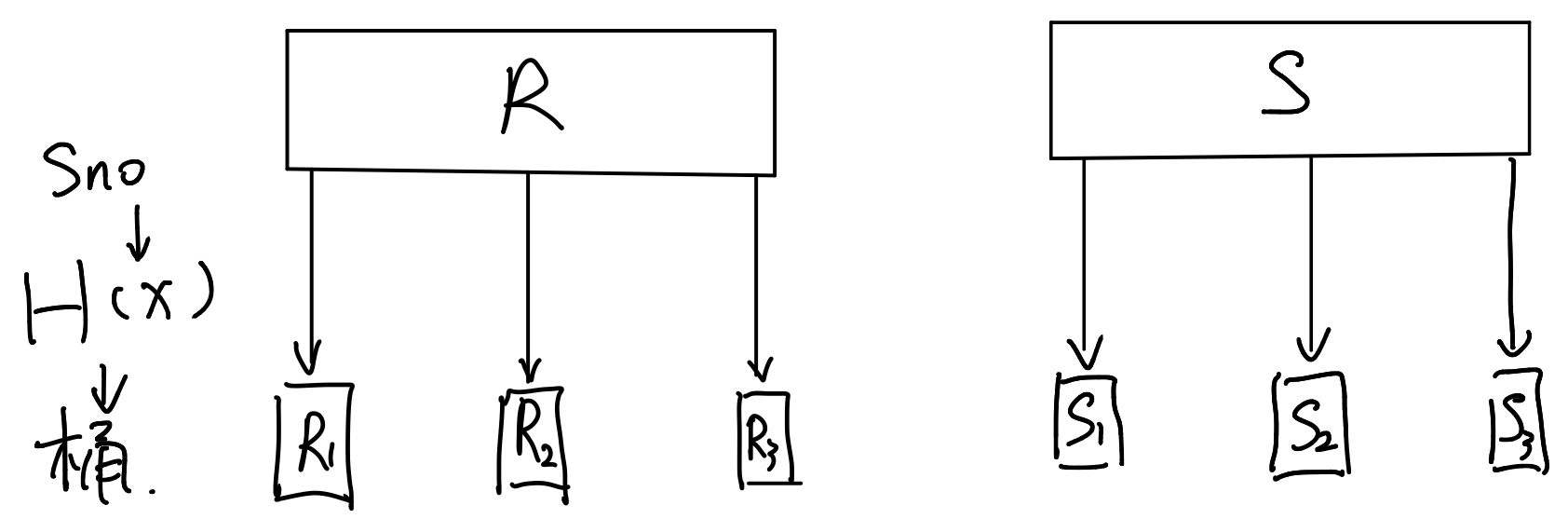
最后我们得到了两组桶，每个桶对应的sno(连接属性)是不一样的。但是，因为我们使用了同样的哈希函数，对于$ R_1S_1$ ,$R_2S_2$ ,$R_kS_k$​​ 所对应的 sno都是相同的。相当于对R表和S表进行了切分，使得两张表内能够连接的元组放在编号相同的桶中。

之后，我们可依次将$R_iS_i$调入到内存当中进行连接操作，然后输出，直到结束

那么这个方法的IO代价是多少呢？首先要做哈希操作的话，需要将R和S都读入内存一遍，记为$B(R),B(S)$

然后需要写出到桶里，写的代价为$B(R),B(S)$

最后要把桶两两之间做一个连接，需要扫描一遍，代价为$B(R),B(S)$

总的来说整个连接操作的IO代价为 $3\times (B(R)+B(S))$

嵌套循环和散列循环相比，哪个效率更高呢？这需要分情况讨论。

• 嵌套循环 ：外表数据量*内表单条（带连接条件）访问性能

• 散列循环 ：内表全结果集（无连接条件）访问性能

如果是内表没有索引，使用hash join

如果是内表是复杂运算后的结果集，使用hash join 。

使用场景

（ 1 ）外表可能记录数相对大

（ 2 ）内表通过连接条件没有合适的索引。

局限

（ 1 ）必须是等值连接

（ 2 ）要求连接条件有一定的区分度。

MYSQL8 中的散列连接

Hash Join 是扫描驱动表，利用 join 的关联字段在内存中建立散列表，然后扫描被驱动表，每读出一行数据，并从散列表中找到与之对应数据。它是大数据集连接操时的常用方式，适用于驱动表的数据量较小，可以放入内存的场景，它对于没有索引的大表和并行查询的场景下能够提供最好的性能。可惜它只适用于等值连接的场景，比如on a.id = where b.a_id

还是上述两张表 join 的语句，其执行过程如下

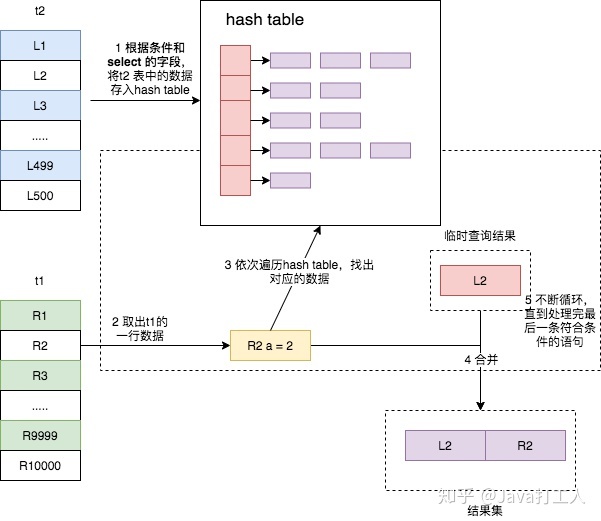
• 将驱动表 t2 中符合条件的数据取出，对其每行的 join 字段值进行 hash 操作，然后存入内存中的散列表中；
• 遍历被驱动表 t1，每取出一行符合条件的数据，也对其 join 字段值进行 hash 操作，拿结果到内存的散列表中查找匹配，如果找到，则成为结果集的一部分。

可以看出，该算法和 Block Nested-Loop Join 有类似之处，只不过是将无序的 Join Buffer 改为了散列表 hash table，从而让数据匹配不再需要将 join buffer 中的数据全部遍历一遍，而是直接通过 hash，以接近 O(1) 的时间复杂度获得匹配的行，这极大地提高了两张表的 join 速度

Sorted Merge Join 算法

Sort Merge Join 则是先根据 join 的关联字段将两张表排序(如果已经排序好了，比如字段上有索引则不需要再排序)，然后在对两张表进行一次归并操作。如果两表已经被排过序，在执行排序合并连接时不需要再排序了，这时Merge Join的性能会优于Hash Join。Merge Join可适于于非等值Join（>，<，>=，<=，但是不包含!=，也即<>）。

需要注意的是，如果连接的字段已经有索引，也就说已经排好序的话，可以直接进行归并操作，但是如果连接的字段没有索引的话，则它的执行过程如下图所示。

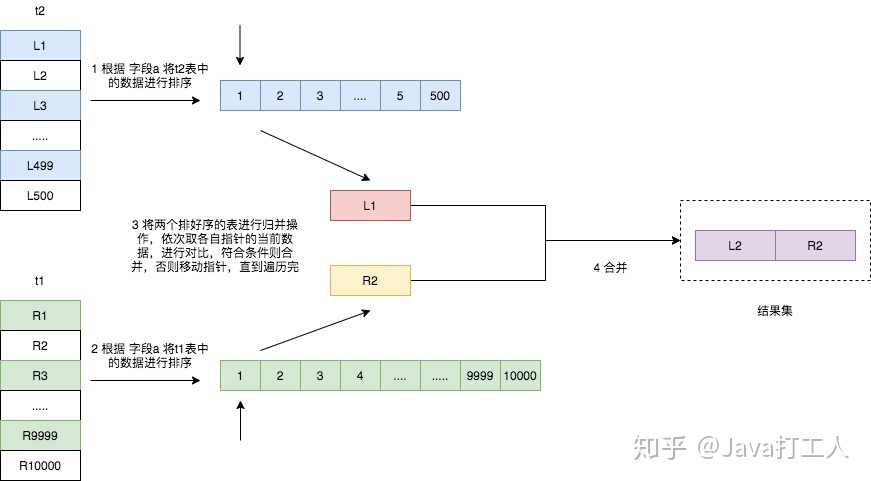
• 遍历表 t2，将符合条件的数据读取出来，按照连接字段 a 的值进行排序；
• 遍历表 t1，将符合条件的数据读取出来，也按照连接字段 a 的值进行排序；
• 将两个排序好的数据进行归并操作，得出结果集。

Sorted Merge Join 算法的主要时间消耗在于对两个表的排序操作，所以如果两个表已经按照连接字段排序过了，该算法甚至比 Hash Join 算法还要快。在一边情况下，该算法是比 Nested Loop Join 算法要快的。

	Nested Loop Join	Hash Join	Sorted Merge Join
连接条件	适用于任何条件	只适用于等值连接	等值或非等值连接，除了$<>$
主要消耗资源	CPU、磁盘I/O	内存、临时空间	内存、临时空间
特点	当有高选择性索引或进行限制性搜索时效率比较高，能够快速返回第一次的搜索结果。此时使用的是Index Nested Loop Join	当缺乏索引或者索引条件比较模糊时，Hash Join比Nested Join 快。在数据仓库环境夏，如果表的记录数多，则其效率高	当缺乏索引或者索引条件模糊时，Sort Merge Join 比 Nested Loop Join有效。当里安桀字段有索引或者提前排好序时，比Hash Join还快，并且支持更多的连接条件
缺点	无索引或者记录多的时候，效率很低	建立哈希表需要大量内存，第一次的结果返回比较慢	所有的表都需要排序，它为最优化的吞吐量而设计，并且在结果没有全部找到前不返回数据
需要索引	是(没有索引效率太低)	否	否