数据流模型及频繁项挖掘
在这一讲我们要学习什么是数据流,什么是数据流算法,怎么去评价一个数据流算法的好坏。
数据流和数据流模型
首先我们要认识数据流,其具有一下几个特征
- 数据总量不受限制,因此我们很难准确估算数据量大小
- 数据到达速率块,比如大型强子对撞机可以每秒产生40EB的数据
- 数据到达次序不受约束,我们无法预测数据的到达次序。
- 除非可以保存,每个数据只能”看“一次。因为很少有系统能把海量的数据都放在内存中,而且数据到达的速度很快,分析的时间很短,否则就会出现数据拥塞
我们可以将数据流看做是一个无限的元组序列 $\sigma=
因此我们对处理数据流的算法也提出了如下要求:
- 实时性:实时、连续地输出查询结果
- 低空间复杂度:数据流规模理论上是无限的,为了保证算法高效稳定运行,需降低算法的空间开销
- 结果准确性:数据规模大,速率快,因此对于一些复杂问题,不太可能通过数据的一次遍历就获得准确答案。在实际应用中,往往不要求精准的查询结果
- 适应性:在很多应用中,涉及多个数据流的处理,需设计具备适应性的算法
| 传统算法 | 数据流算法 | |
|---|---|---|
| 数据类型 | 有限&静态 | 无限&动态&高速 |
| 存储 | 硬盘 | 内存&空间限制 |
| 效率 | 非实时 | 实时& Ad-hoc |
| 返回值类型 | 精确/近似 | 近似 |
因为数据流的大小是不确定的,因此我们希望算法的空间消耗和时间消耗是次线性的($O(\log n)$),或者与流的大小无关。
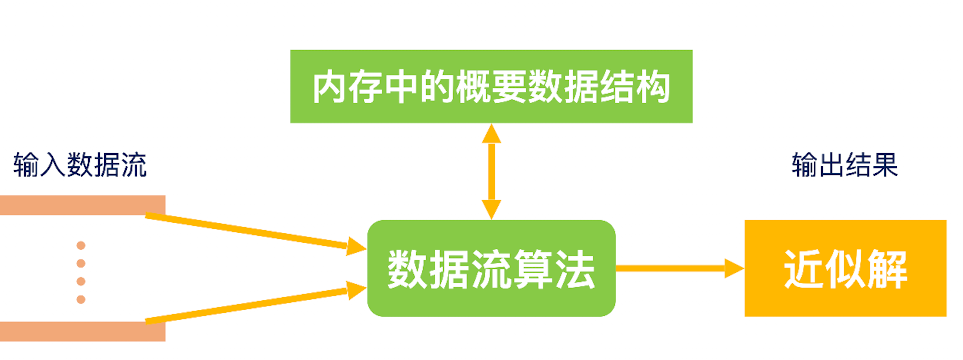
数据流子模型
按照数据流中数据元素对数组A的不同影响方式划分
数据流模型可以划分为三个子模型:时间序列模型,收音机模型,十字转盘模型
- 时间序列模型。每个数据项 $a_i = A[i]$ 按照i增加的顺序出现,相当于时间序列
- 收音机模型。每个数据项$ai=(j,I_i),I\geq 0$ 表示对$A[i]$的增量,即$A_i[j] = A{i-1}[j]+I_{i_0}$ 如同多个收音机一样,多个$a_i$ 表示一段时间上$A[j]$的增量。这是一种更为普遍的数据流模型
- 十字转盘模型。每个数据项$ai= (j,U_i)$ 表示对$A[j]$ 的更新,即 $A_i[j]=A{i-1}[j]+U_i$ ,其中$U_i$可正可负。该模型适合描述数据流动态的出入状态,单位时间内流入和流出的数量不必相同
按照数据流上个元素的重要程度划分
数据流可以分成另外三种子模型:界标模型、滑动窗口模型、衰减窗口模型
- 界标模型。如下图,界标模型有起始点和终止点两个时间点。其中起始点是固定的,终止点随时间推移而不断递增。在界标的任意终点和起点之间,数据的重要性均等。这是最容易理解的模型

- 滑动窗口模型。令W为窗口大小,在这个模型中,数据流算法仅仅考虑最近的W个元素,即查询范围是$[\max (0,d-W),\cdots,d-1]$ .处在查询范围之外的元素其重要性为0;处在查询范围之内的元素重要性均等。滑动窗口模型也有起始点和终止点,但是会随着时间的推移而同步递增。

- 在这个模型中,数据流算法的范围是$[0,\cdots,d-1]$ 。处在查询范围中的各个元素的重要程度是不同的。新到达的元素,其重要程度比较高;到达时间较长的元素,其重要程度较低

近似算法与随机算法
由于存储空间和时间的限制,我们在数据流上做到精确计算非常困难。
近似算法:寻找误差在一定范围内的近似解。之前我们学的Morris算法、布隆过滤器以及局部敏感哈希算法,都是近似算法
- 比如说,寻找一个误差在10%以内的解
- 比如说:近似解落在真实值的$(1\pm \epsilon)$ 范围内,其中$\epsilon=0.1$
随机算法:比近似算法更加宽松,是允许小概率失败的(即不在误差范围内)
- 例如,估计值有 1/100 的概率不在误差范围内,即成功地概率为$1-\delta$ ,其中$\delta = 0.01$
我们可以这样来理解: 随机算法就等于 $(\epsilon,\delta)$-近似算法 ,接下来会详细介绍各种类型的近似算法
$\epsilon$-近似算法(相对误差)
其实很好理解,我们假设数据流$\sigma$和其精确输出$\xi(\sigma)$,其近似算法的输出记为$\mathcal{A}(\sigma)$ 。那么如果是相对误差版本的话:
$\epsilon$-近似算法(绝对误差)
绝对误差更好理解,就是要把误差控制在$\epsilon$里面 ,即
$(\epsilon,\delta)$-近似算法(相对误差)
$(\epsilon,\delta)$ 近似算法往往比$\epsilon$近似算法更加宽松一点,它只要大部分情况下算法给出的估计值满足$\epsilon$近似即可。即:
用语言来解释就是说一个$(\epsilon,\delta)$ 近似算法的数据结果可能会出现 $|\mathcal A-\xi (\sigma)|>\epsilon\xi(\sigma)$的情况,但这种情况发生的概率不会超过$\delta$
$(\epsilon,\delta)$-近似算法(绝对误差)
当然,我们也可以给出绝对误差版本的定义
这是一个数据流分析挖掘框架:
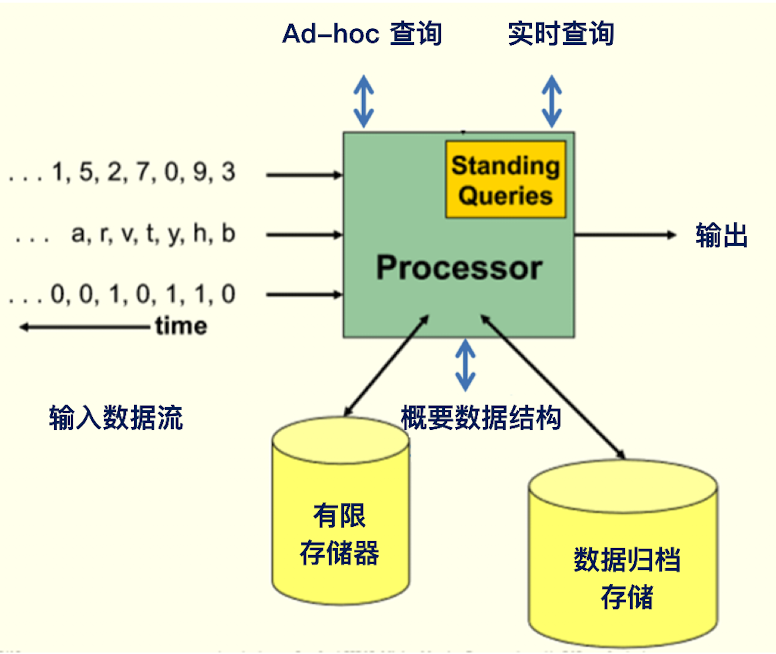
频繁项挖掘
我们本章的重点就在于找到数据流的频繁项,接下来要介绍的一些算法都是围绕这频繁项展开的。那么首先我们就来介绍频繁项估计
定义
在数据流$\sigma =
其中,n为该数据流中不同元素的个数,$fi$ 为元素$a_i$ 的频数,且满足$\sum{i=1}^nf_i = m$
然后,我们可以找出满足需求的元素,比如频繁项。
- 对于大多数问题,如果$\exists a_j : f_j > m/2$, 则输出$a_j$, 否则输出空集$\empty$
- 频繁项:给定一个参数k,输出频繁元素集合${a_j:f_j\geq m/k}$; 或者给定一个参数$\psi$,输出频繁元素集合 ${a_j:f_j>\psi m}$
比如说:对给定的数据流$\sigma =
- $\sigma$中不存在大多数问题,因为没有大于4的元素
- 当k等于4的时候,m/k=2,因此频繁项为a,b,c
- 当$\psi=0.3$ 时候,$m\cdot \psi = 2.4$,因此频繁项为a
确定性近似频数算法 Misra Gries
Misra Gries算法是一个确定性求解频繁元素的近似算法。其思想和俄罗斯方块非常类似,伪代码如下:
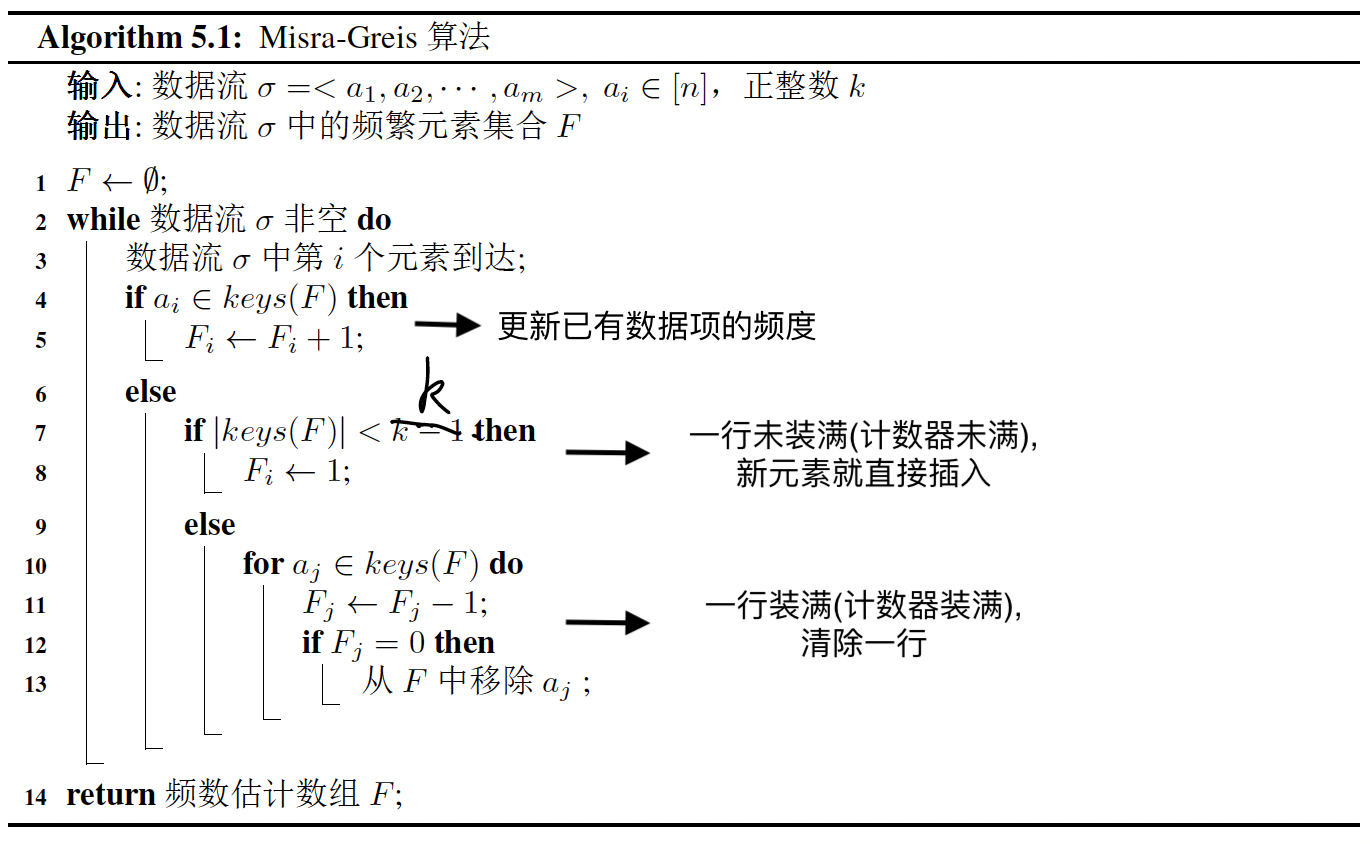
算法的输入流$\sigma =
该算法的核心思想如下:
- 对到达的元素$a_m$,如果已经为其创建了计数器,便将相应的计数器加1;
- 如果没有相应的计数器,且计数器的个数少于k(意味着内存中还有足够的空间创建新的计数器),那么则为该元素分配一个新的计数器,并置为1;
- 如果当前计数器的个数为k (意味着内存中已经没有足够的空间来创建新的计数器),则把所有计数器减1,然后删除值为0的计数器
给出一个例题:
给定输入流$
| 输入 | 操作 | 结果 |
|---|---|---|
| b | 插入 | $F={(b,1)}$ |
| a | 插入 | $F={(b,1),(a,1)}$ |
| c | 插入、删除 | $F={(a,1),(b,1),(c,1)}\Rightarrow F={}$ |
| a | 插入 | $F={(a,1)}$ |
| d | 插入 | $F={(a,1),(d,1)}$ |
| e | 插入、删除 | $F={(a,1),(d,1),(e,1)}\Rightarrow F={}$ |
| a | 插入 | $F={(a,1)}$ |
| f | 插入 | $F={(a,1),(f,1)}$ |
| a | 更新 | $F={(a,2),(f,1)}$ |
| d | 插入、删除 | $F={(a,2),(f,1),(d,1)}\Rightarrow {(a,1)}$ |
算法分析
在 Misra Gries 算法中,算法最后的输出结果可能是不频繁的。试想,如果最后一个元素是数据流中一个新出现的元素,而且最后一个元素到达后,k位置中还有空位,那么这个新元素会出现在最后的结果中。也就是说,Misra Gries算法可能会出现误报。虽然可能出现误报,但是频繁元素一定在最后的输出结果中。
不能否认,Misra Gries算法是一个构思非常巧妙的算法,只需要k个计数器就能找到一个数据流中所有的频繁项元素。
随机近似频数算法 Counting Sketch
对于给定的数据流,Misra Gries 算法输出的结果中,每个元素的频数是无从知晓的,而随机近似频数算法Count Sketch 则可以估计频繁元素的频数。
简单抽样算法
首先我们来介绍一下简单抽样算法。这是一种非常简单的计算元素频数的算法。该算法的核心思想是:对于到达的元素$a_i$, 以概率 $p=M/m$ 对该元素的频数+1.其中,M表示抽样后的数据流大小,m表示原数据流大小。伪代码如下:

比如说现在给定一个数据流$<2,2,1,2,2,4,5,4,4,2>$ ,$p=\frac{1}{3}$ ,如下图所示,估计元素2的频数为:$f’(2)=\frac{c_2}{p}=6$
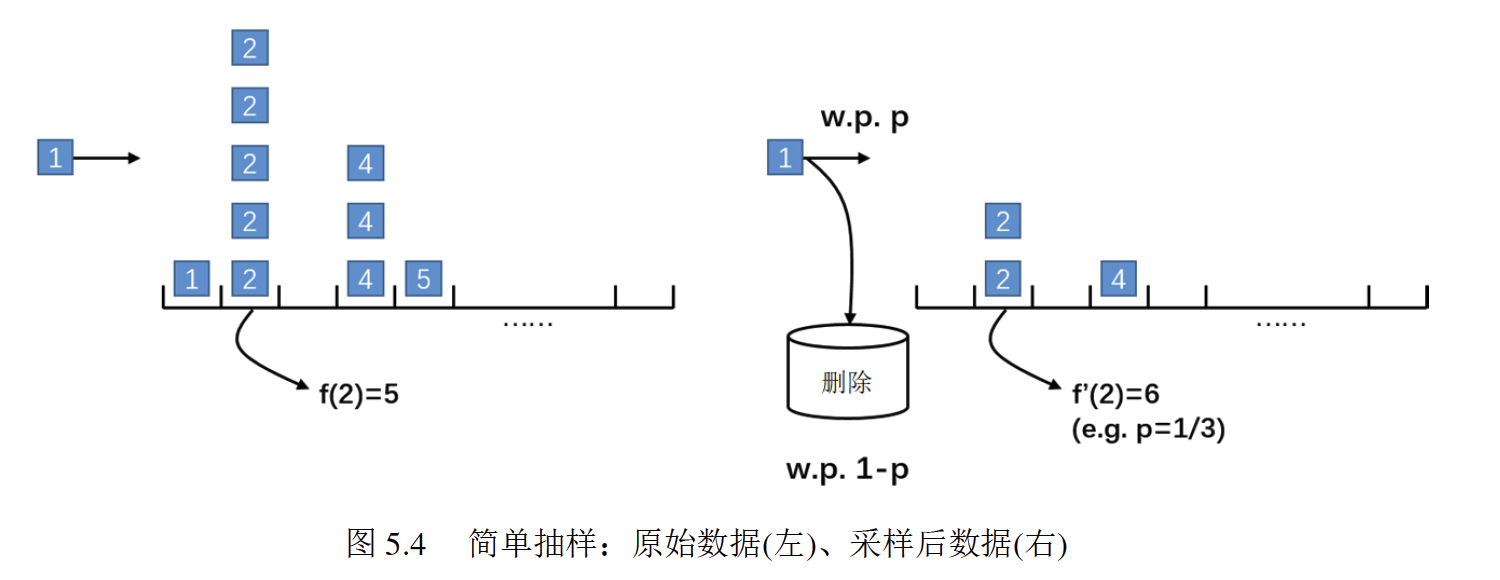
算法分析
简单抽样算法称为 $(\epsilon,\delta)-$近似算法的空间需求是: $M = O(\frac{m\log {1}/{\delta}}{\epsilon^2})$ ,其中,m为原数据流的大小,$\epsilon$是误差因子,$\delta$是控制误差在一定范围的尾概率上界。
从空间需求看出,简单抽样算法所需空间与数据流大小有关,当数据流规模较大时,该算法所需的空间必将大幅增加。因此我们需要提出更高效的基于概要数据结构的频数估计算法
Basic Count Sketch算法
从简单抽样算法的空间需求来看,找到一个更为紧凑的数据结构来维护数据流中高频元素的近似计数时非常必须的。
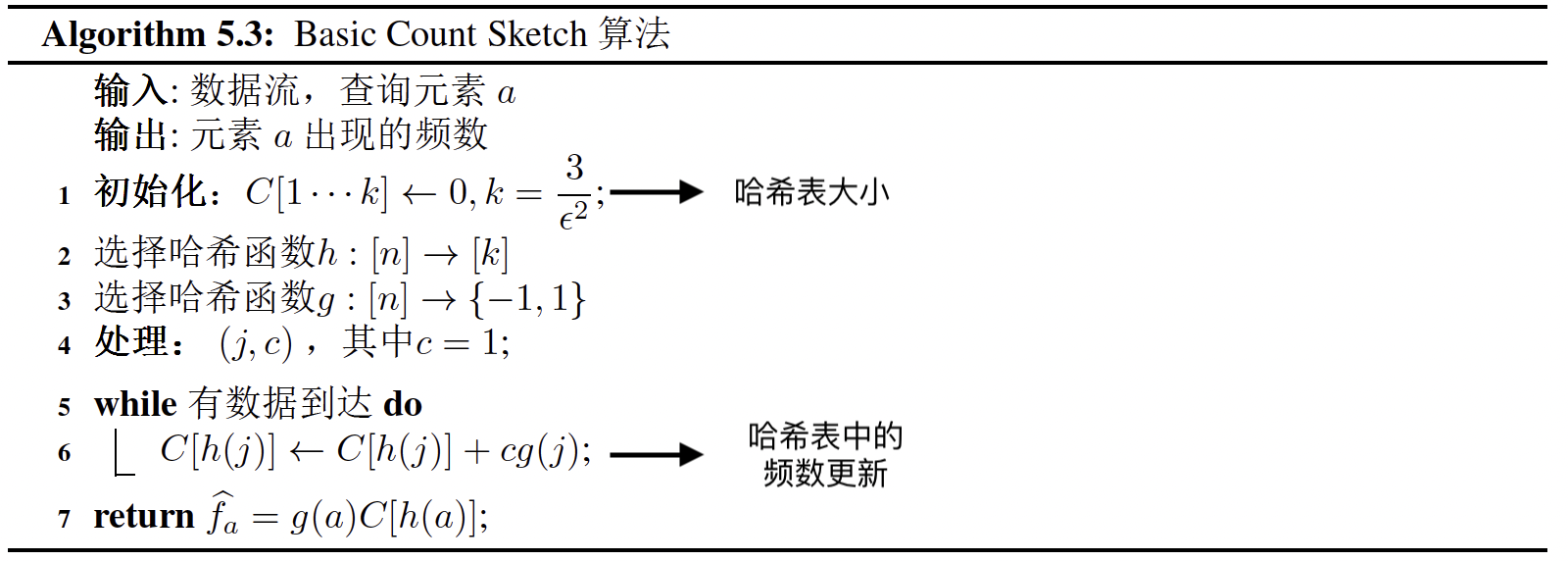
Basic Count Sketch 算法维护一个计数数组C 和两个哈希函数$h(\cdot),g(\cdot)$。 哈希函数$h(\cdot)$将n个元素均匀的映射到k个位置(算法第二行);哈希函数$g(\cdot)$将n个元素映射为$-1$或者$+1$(算法第三行)。
对于一个新到达的元素,将其位置上的计数加1或者减1,对于查询元素a,估计出的频数为 $\hat f_a = g(a)C[h(a)]$
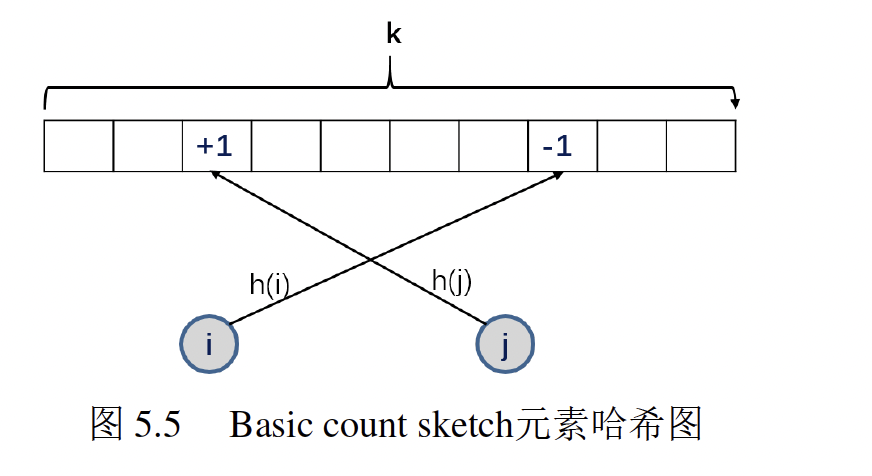
两个哈希函数的操作如图所示。对于元素i,$h(i)$将其映射到第7个位置上,$g(i)$控制该位置计数减1;对于元素了$j$ ,$h(j)$将其映射到第2个位置上,$g(j)$控制该位置计数加 1。
比如说现在有一个数据流 $
但是只有两个计数器(只有两个位置来存放频数),因此设计一个哈希函数,使得$h(a)=h(b)\neq h(c)$, 我们用这个算法来计算各个元素的频数:
首先,我们还要知道一共有8种($2^3$)可能的哈希函数$g(\cdot)$来使得${a,b,c}\rightarrow {-1,+1}$,如下图:
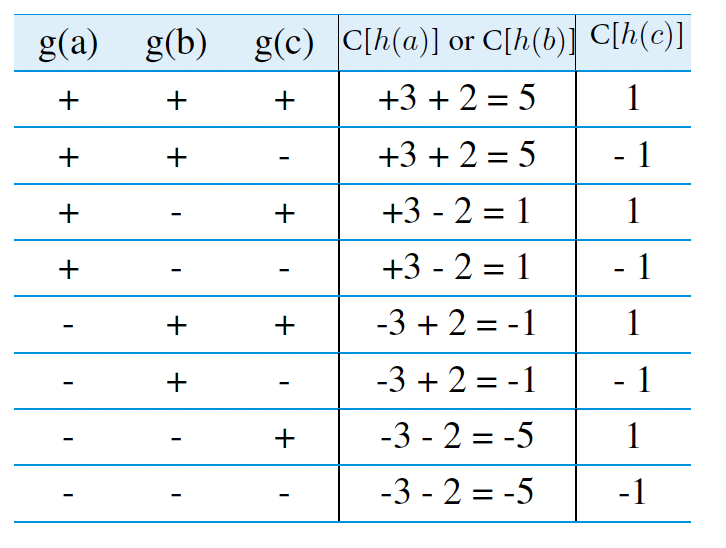
比如说对于第一种哈希函数, $g(a),g(b),g(c)$都是$+1$,因为$h(a)$和$h(b)$在同一个位置上,所以凡是遇到$a$和$b$,就在这个位置上+1,最后得到的频数为5;$h(c)$是另外一个位置,且只出现了一次,因此最后得到的频数为1
那么我们穷举8种 $g(\cdot)$,最终得到了上表,接下来我们要对$a,b,c$三个数的频数进行分别计算。
根据 算法$\hat f_a = g(a)C[h(a)]$,我们对8个哈希函数的结果求均值,如下:
可以看到,在经过多次实验(取多次不同哈希函数)之后,频数的估计和实际频数相同,这并不是一个巧合
对于每一个 $j\in [n]$ ,根据h函数哈希的结果,定义一个指示变量$Y_j$ 如下:
这里的$Y_j$是一个随机变量,表示元素j与元素a是否哈希到了同一个位置。最终,对元素a的频数估计是计数器$h(a)$位置的值。因此所有哈希到h(a)位置上的元素都对元素a的频数估计起到了作用,因此:
如果只有1个计数器
同样是上面的数据流 : abcaba, 如果只有一个计数器会怎么样?
| g(a) | g(b) | g(c) | C[h(a)]=C[h(b)]=C[h(c)] |
|---|---|---|---|
| + | + | + | 3+2+1= 6 |
| + | + | - | 3+2-1=4 |
| + | - | - | 3-2-1= 0 |
| + | - | + | 3-2+1=2 |
| - | - | + | -3-2+1=-4 |
| - | - | - | -3-2-1=-6 |
| - | + | - | -3+2-1=-2 |
| - | + | + | -3+2+1 = 0 |
Count Sketch算法
Count Sketch 算法基于$t$次频数估计的中位数和真实值很接近的想法,在Basic Count Sketch 算法的基础上,将哈希函数$h(\cdot)$个数增加到$t$个,将每个元素映射到 $t$ 个位置上,同时也有t个函数决定每个位置上的计数加1或者减1。(这里,$t = \log(1/\delta)$)
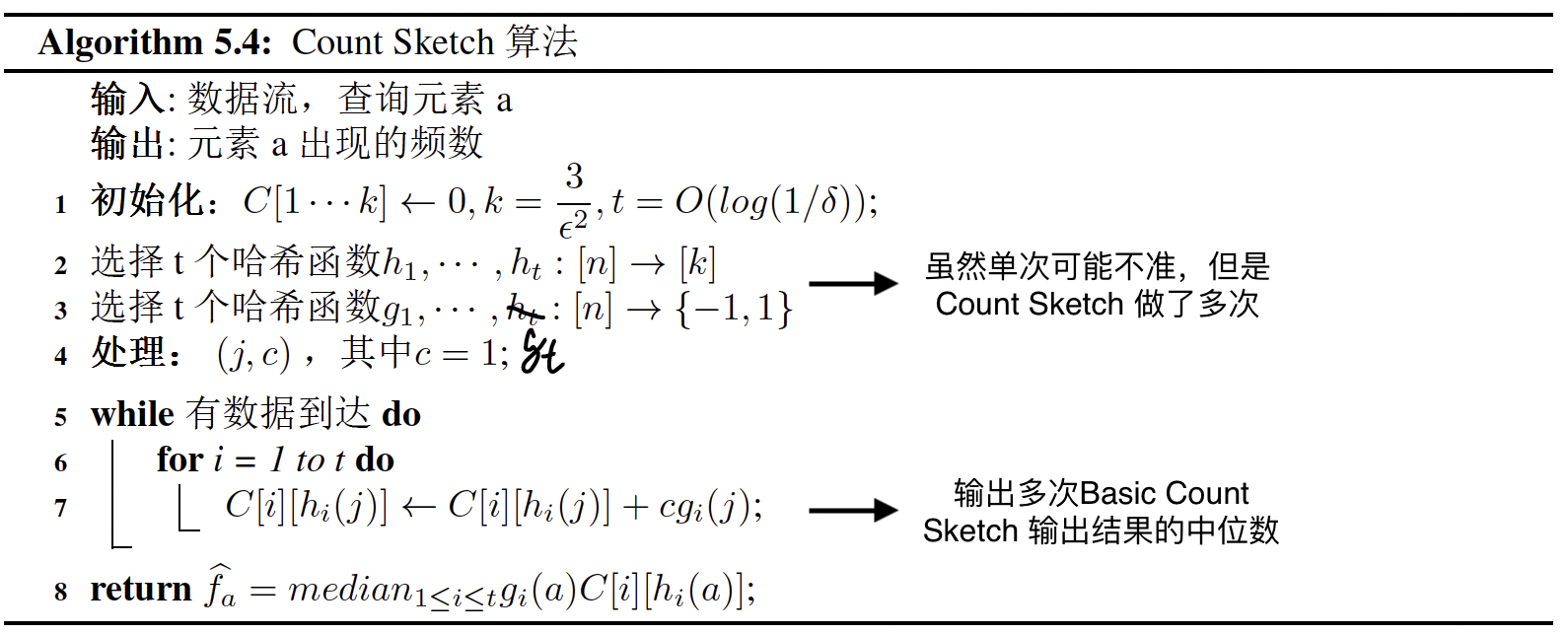
Count Sketch 算法最终是一个空间消耗为$O(\frac{\log ({1}/{\delta})}{\epsilon^2})$ 的 $(\epsilon,\delta)$近似估计
哈希函数个数是 $t = O(\log(1/\delta))$
Count-min Sketch算法

在CM-sketch算法中,其数据结构是一个宽度为w,深度为d(代表哈希函数的个数)的计数器数组:
初始化时,每个元素均为0. 另有d个哈希函数使得:
一旦w和d确定下来,CM-sketch所需要的空间便确定了,我们发现哈希表相对于Count Sketch的($\frac{3}{\epsilon^2}$)更加小了 ,因此空间性能提升了$1/\epsilon$ 倍左右。
例题
给定数据流$<4,1,3,5,1,3,2,6,7,0,9>$, 若哈希函数形如 $h(x)=(ax+b) ~\text{mod~} 8$ ,其中a和b是任意给定的常数。假定给定如下哈希函数:
试解答以下问题:
- 利用 Count-Min Sketch 算法估计频繁项
这种情况下,$d=3,w=8$
| 哈希值表 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| $h_1(x)$ | 2 | 5 | 0 | 3 | 6 | 1 | 4 | 7 | 5 |
| $h_2(x)$ | 5 | 4 | 3 | 2 | 1 | 0 | 7 | 6 | 4 |
| $h_3(x)$ | 3 | 0 | 5 | 2 | 7 | 4 | 1 | 6 | 0 |
对于三个哈希函数, 将上述哈希到整个表中的不同位置并计数
比如说,第一个到达的数据是4,那么查询上面的哈希值表,在4这个位置,$h_1(x) = 6,h_2(x)=1,h_3(x)=7$ ,那么我们就在下面这个dw表格中,在$h_1(x) = 6,h_2(x)=1,h_3(x)=7$ 的位置上分别加上1。
这样,把整个数据流过一遍,就得到了下面这张表格
| dw表格 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| $h_1(x)$ | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 1 |
| $h_2(x)$ | 1 | 1 | 2 | 1 | 3 | 1 | 1 | 1 |
| $h_3(x)$ | 3 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
然后,对于每一个元素,我们都要取到哈希到的格子中的最小值
- 比如说对于元素0,哈希到$h_1(x)=2,h_2(x)=5,h_3(x)=3$ 这三个格子,格子中的值分别是1、1、1,最小值为1,因此对元素0的频数估计为1.
- 比如说对于元素1,哈希到$h_1(x)=5,h_2(x)=4,h_3(x)=0$ 这三个格子,格子中的值分别是3、3、3,最小值为3,因此元素1的频数估计为3
以此类推,得到:
这里不存在大多数项。因为没有频数大于4的元素
当$k=3$时,大于$8/3=2.6$的元素就可以被认为是频繁项,因此 1和9是频繁项
当$k=4$时,大于$8/4=2$的元素就可以被认为是频繁项,因此 1、3、9是频繁项。
但是我们知道在这个数据流中9只出现了1次,因此这个算法也存在误判的概率,这就是一次collision。Count-min Sketch的确会有这种问题,因为这个模型是从Bloom Filter衍生过来的。所以说Count-min Sketch是一个概率模型,返回的结果是一个上限值(upper-bound)。
- 给定任意元素i,题⽬中的CM Sketch可以达到何种精度
因为 哈希函数 $k = \lceil \log(1/\delta) \rceil = 3$ 因此 $ \frac{1}{8}<\delta<\frac{1}{4}$, 也就是说,算法错误的概率在 $12.5\%—25\%$ 之间;
数组宽度 $d = \lceil 2/\epsilon\rceil =8$ ,$\frac{1}{4}<\epsilon <\frac{2}{7}$,也就是说,算法估计精度误差在 $25\%—28.6\% $ 之间
- 如果想找到$(\epsilon,\delta)$ 估计,需要如何修改算法?(从哈希函数的个数入手)
可以增加数组宽度,达到更高的算法精度
也可以增加哈希函数的个数,达到更高的准确度
算法解释
在算法开始时,构造一个d行w列的空数组,可以认为每一行是独立的,算法在运行时同时记录了d个这样的数组。在每出现一个流数据的时候,对每一个数组进行一次更新,注意元素的第二个下标用的是数据的哈希值。
算法在运行的过程中可能产生冲突,也就是两个不同的流数据的哈希值可能相同,这个时候就会导致结果偏大,但是因为有相当于t次的重复计算,通过取最小值的方法来进行一些弥补,但是这样的方法也不能完全避免冲突。
算法分析
设计一个最优的 Count-min Sketch模型的过程是:
- 估算数据流n 的大小
- 选择一个合理的 $\epsilon$ 值
- 选择一个合理的概率值 $1-\delta$
- 哈希函数的个数 $k = \lceil(\ln\frac{1}{\delta})\rceil$, 数组的宽度 $w = \lceil\frac{2}{\epsilon}\rceil$
可以看出,要想错误范围越小,就需要更大的w,也就是表格的宽度
想要更高的概率,就需要更大的k,也就是更多的哈希函数
假设我们现在需要为 $10^6$ 的数据计数,规定精度 $\epsilon = 0.002$ ,由此可知 $d = 1000$ ; 规定准确率为$99\%$ , 可知$\delta = 0.01$, 因此需要的哈希函数个数为 $k = \lceil(\ln100)\rceil= 5$
假设每个计数单元占内存大小为 4 byte,那么,该模型将占用内存
总结
几种方法的总结
| 算法 | 空间需求 | 参数 |
|---|---|---|
| 简单抽样算法 | $M = O(\frac{m\log(1/\delta)}{\epsilon^2})$ | m:数据流大小 $\delta$: 误差 $\epsilon$: 估计精度 |
| Basic Count Sketch算法 | $M = O(\frac{1}{\delta\epsilon^2})$ | 和数据流大小无关,确定精度和误差即可 计数器个数 $k = \frac{3}{\epsilon^2}$ |
| Count Sketch算法 | $M = O(\frac{log(1/\delta)}{\epsilon^2})$ | 相比于Basic Count Sketch,更低 计数器个数 $k=\frac{3}{\epsilon^2}$ 哈希函数个数 $t = \lceil \ln(1/\delta)\rceil$ |
| CM Sketch算法 | $M = O(\frac{log(1/\delta)}{\epsilon})$ | 复杂度最低,计数器减少 数组的宽度 $w = \lceil\frac{2}{\epsilon}\rceil$ 哈希函数的个数 $k = \lceil(\ln\frac{1}{\delta})\rceil$ |