数据科学算法ch7-随机游走

随机游走

引入

首先我们来复习一下联合概率分布

给定n个离散随机变量 $X_1,X_2,\cdots,X_n$ 分别取值为$x_1,x_2\cdots,x_n$的联合概率 $f(x_1,x_2\cdots,x_n)$ 表示为：

$$f(x_1,x_2\cdots,x_n) = P(X_1 = x_1,X_2= x_2,\cdots,X_n=x_n)$$

如果n个离散随机变量$X_1,X_2\cdots,X_n$ 是相互独立的，那么它们取值$x_1,x_2\cdots,x_n$ 的联合概率可以很方便得计算为

$$f(x_1\cdots,x_n) =\prod_{i=1}^nP(X_i=x_i)=\prod_{i=1}^n f_{X_i}(x_i)$$

但是，如果$X$之间并不相互独立，那么

$$f(x_1,\cdots,x_n) = \prod_{i=2}^m P(X_i = x_i|X_{i-1}=x_{i-1},\cdots,X_1 = x_1)\\$$

这就是链式法则

但是，对于大规模的数据，会很难处理，因为联合概率的计算复杂度会非常高。此时，需要对数据间的相关关系进行简化。对文本数据或者音频数据建模时，常常假设序列数据点之间存在一阶相关关系，即

$$P(X_i = x_i|X_{i-1}=x_{i-1},\cdots,X_1 = x_1) =P(X_i = x_i |X_{i-1}=x_{i-1})$$

因为有些词常常是一前一后出现的。比如在”今天天气炎热，我们去游泳“这一句话中，”天气”与“炎热”这两个词常常一前一后出现，但是“天气”和”游泳”不太可能会出现前后出现。

同样的，对股票价格数据建模时，会假设序列数据点之间存在t阶相关关系，即

$$P(X_i = x_i|X_{i-1}=x_{i-1},\cdots,X_1 = x_1) = P(X_i = x_i|X_{i-1} = x_{i-1}\cdots,X_{i-t}=x_{i-t})$$

随机过程

现在我们来学习随机过程，随机过程${X(t,\omega),t\in T ,\omega\in \Omega}$ 是与时间t有关的一个随机变量序列，现实生活中有很多问题都可以用随机过程来建模，比如说文本数据、语音数据、股票价格和用户上网行为等等。

例子	时间集合	状态空间
浏览网页	步数	所有网页
自然语言	单词位置	字典
股票价格	交易日	价格
赌博	下注次数	筹码数量
液体分子	时间	容器空间

现在我们来具体讲几个随机过程的例子：

抛币游戏

游戏规则：

• 假设开始有 $10, 参加一场公平无限期抛硬币游戏
  • 正面朝上，赢得1
  • 反面朝上，输掉1
• 我们用$X_n$ 表示n次抛币后手上剩余的美元
• 如果$X_0 = 10$,则 ${X_n:n\in N}$ 构成一个随机序列
  • 假设$Xn = 12$，则$X{n+1}=11$或者13
  • 在第(n+1)次抛币后手上剩余的美元和$X{n-1}$​​​​​值没有关系。是一阶相关关系，即：$P(X{i+1} = x{i+1}|X{i}=x{i},\cdots,X_1 = x_1) = P(X{i+1} = x{i+1}|X{n} = x_{n})$​​​​​

在这个抛币游戏中，手上剩余的钱是一个随机过程

• 时间：抛币次数
• 状态：非负集合

在这个游戏中，稳定状态就是输光所有的钱

象棋

象棋中帅的位置变化

• 按照规则，帅在每个位置都可以向周围移动
• $X_n$ 表示n步后帅所在的位置
  • 如果 $Xn = 2$, 则$X{n+1}=1,3,5$
  • $(n+1)$步帅所在的位置和$X{n-1}$ 的值没有关系，即：$P(X{i+1} = x{i+1}|X{i}=x{i},\cdots,X_1 = x_1) = P(X{i+1} = x{i+1}|X{n} = x_{n})$​

因此${X_n:n\in N}$ 构成一个随机过程

• 时间：步数
• 状态：1到9之间的整数

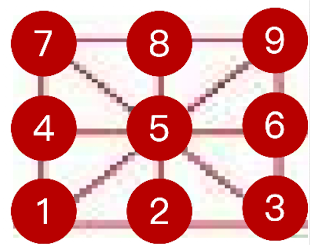
网页浏览

每个网页都有可能对外的锚连接，

• $X_n$ 表示n步之后停留的页面
  • 如果$X=ECNU$， 则$X_{n+1}$ 可以是 MOE、DASE、或者SEI
  • (n+1)步停留的页面和 $X{n-1}$的所停留的页面无关，即$P(X{i+1} = x{i+1}|X{i}=x{i},\cdots,X_1 = x_1) = P(X{i+1} = x{i+1}|X{n} = x_{n})$

因此${X_n:n\in N}$ 构成一个随机过程

• 时间：步数
• 状态：所有网页组成的集合

马尔科夫过程

马尔科夫性质

如果随机过程 ${X(t)\in S,t\in I }$​ , 满足

$$P(X(t_{n+1}) = x_{n+1}|X({t_0})=x_{0},\cdots,X(t_n) = x_n) = P(X(t_{n+1}) = x_{n+1}|X(t_{n}) = x_{n})$$

其中，$t0<t_1<\cdots<t_n<t{n+1}\in I,x_i\in S$​,则称该随机过程满足马尔科夫性质

• 如果 $tn$ 表示当前时间，$t{n+1}$ 表示将来，$t1,\cdots,t{n-1}$ 则表示过去
• 可以理解为：已知现在，将来与过去独立

之前我们说的，咖啡溶质的扩散、网络、赌博、象棋，都是满足马尔科夫性质

马尔科夫过程

若随机过程满足马尔科夫性质，则称其为马尔科夫过程

设 ${X(t),t\in T}$ 的空间状态为S，如果$\forall n \geq 0,\forall t0<t_1<\cdots<t_n<t{n+1}\in T$,在条件 $X(ti) = x_i,x_i\in S,i=0,1\cdots,n$ 下，$X(t{n+1})$ 的条件概率刚好等于在条件$X(t_n)=x_n$ 下的条件概率，即：

$$P(X(t_{n+1}) = x_{n+1}|X({t_0})=x_{0},\cdots,X(t_n) = x_n) = P(X(t_{n+1}) = x_{n+1}|X(t_{n}) = x_{n})$$

则称${X(t),t\in T}$ 为马尔科夫过程

马尔科夫链

马尔科夫链是特殊的马尔科夫过程，它满足：

• 离散的时间集合：步数、下注次数
• 离散的状态空间：网页、计数

因此，布朗运动是马尔科夫过程，但不是马尔科夫链。

在本章举的例子，马尔科夫过程等于马尔科夫链

转移概率

假定随机游走的状态空间为 $\Omega =[n]$ 矩阵 $\bold{P}^{(t+1)}\in\mathbb R^{n\times n}$ 被称为该随机游走的第(t+1)步概率转移矩阵，如果$p{x,y}^{t+1} = P(X{t+1}=y|X_t=x)$​

• 其中 $p_{x,y}^{(t+1)}$ 表示在$(t+1)$ 步随机游走从状态x转移到y的概率
• 概率转移矩阵的每行概率和为1，即：

$$\sum_y p_{x,y}^{t+1} = \sum_{y} \frac{P(X_{t+1}=y|X_t= x)}{P(X_t = x)}=1$$

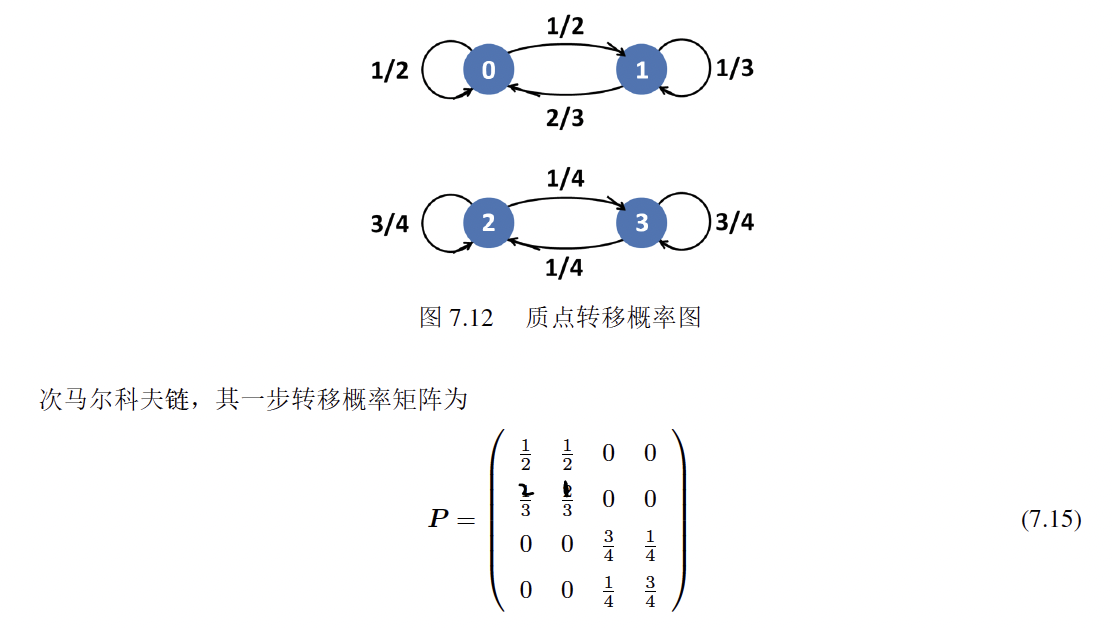
齐次马氏链

如果随机游走满足：

$$P(X_{t+s}=y|X_t = x)= P(X_s = y|X_0 = x)$$

• 即经过t步后，从状态x走到状态y的概率与起始步数s无关，则该随机游走是齐次的

也就是说，无论当前是第几步，只要起点相同，一步转移到目标顶点的概率是相同的马氏链被称为齐次马氏链。

例如：在抛币游戏中，无论是开始手上有10元，还是第100次抛币之后手上有10元，下一步手上有11元的概率是相通的，也就是说，抛币游戏中的马氏链是齐次的。也就是说是无记忆性的

例如：

给定图$G=(V,E)$ 如上图，假设$S=\mathbb Z$ ，无论当前是什么时刻，只要当前在状态a，那么下一步的转移概率为：

$$p_a(a-1)=\frac{1}{2}\\p_a(a+1)=\frac{1}{2}\\p_{ab} = 0(b\neq a\pm 1)$$

因此，这个马尔科夫链也是齐次的。如果$\pi(a)$ 表示该马尔科夫链初始时刻在状态a的概率，那么$\pi(10)=1,\pi(a)=0(a\neq 10)$ 意味着在时刻0马尔科夫链一定是从坐标10出发的

随机游走

在学习随机游走之前我们需要了解以下定义：图、度、无向图、路劲、连通分量、邻接矩阵、邻接表

现给出随机游走的定义：随机游走模型是针对图建立的抽象马氏链模型，因此图上的马氏链都可以被称为随机游走。图上的随机游走是指给定一个图和一个出发点，随机地选择一个邻居节点，移动到邻居节点上，然后把当前节点作为出发点，重复以上过程。那些被随机选出的节点序列就构成了一个该图上的随机游走。

我们可以将随机游走和之前说的齐次马尔科夫链结合起来理解：现在有状态转移图如下：

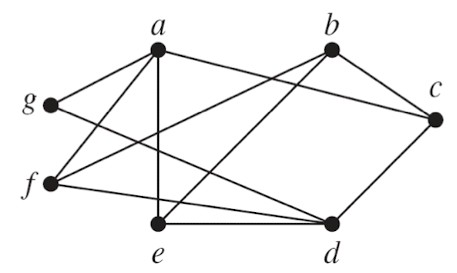
假设$\pi(a) = 1,\pi(i) = 0(i\neq a)$ 意味着在时刻0该随机游走从状态a出发。在第一步，该随机游走可能到达顶点c、e、f、g. 随机游走会随机选择一个顶点，其中：

$$p_{ac}=p_{ae}=p_{af}=p_{ag}= \frac{1}{4}\\$$

走到第二个点，又有好几种不同的选择。以此类推，可以得到在图G上的一个随机序列。因此，随机游走是一类特殊的马氏链

无论何时出发，只要当前停留在状态a,那么下一步到达c、e、f、g的概率是相同的。因此，该随机游走对应的马氏链也是齐次的

平稳分布

之前我们说了概率转移矩阵，基于概率转移矩阵我们提出了平稳分布的概念。

状态分布

我们令$\pi^{(t)}$为状态空间为S的马氏链在时刻t的状态分布，即：

$$\pi_x^{(t)} = P(X_t = x)$$

特别地，将$\pi^{(0)}$ 称为初始分布。

进一步，对于一个概率转移矩阵为P的马氏链，其状态分布$\pi^{(t)}$ 具有如下性质

• $\pi^{(t)}$​ 的每个分量满足$0\leq\pi_i^{(t)}\leq 1$
• $\sum_{j\in S}\pi_j^{(t)} = 1$ 即每行的和为1
• $\pi^{(t+1)}= \pi^{(t)}P(t)$

比如对于矩阵：

$$P=\begin{pmatrix}\frac{1}{2}&\frac{1}{2}&0&0\\\frac{1}{3}&\frac{2}{3}&0&0\\0&0&\frac{3}{4}&\frac{1}{4}\\0&0&\frac{1}{4}&\frac{3}{4} \end{pmatrix}$$

我们给定第t步的状态分布为$\pi^{(t)}=(0.4,0.6,0,0)$,那么:

$$\pi^{(t+1)} = \pi^{(t)} P = (0.4,0.6,0,0)\\$$

我们给定第t步的状态分布为$\pi^{(t)}=(0,0,0.5,0.5)$​,那么:

$$\pi^{(t+1)} = \pi^{(t)}P=(0,0,0.5,0.5)\\$$

我们给定第t步的状态分布为$\pi^{(t)}=(0.1,0.9,0,0)$​​,那么:

$$\pi^{(t+1)} = \pi^{(t)}P=(0.35,0.65,0,0)\\$$

平稳分布

对于一个转移概率矩阵为$\boldsymbol P$ 的有限状态马氏链，若状态分布$\pi$满足：

$$\pi\boldsymbol P = \pi$$

则称$\pi$​ 为该马氏链的平稳分布·

有矩阵为 $P =\begin{pmatrix}\frac{1}{2}&\frac{1}{2} \\frac{1}{4}&\frac{3}{4} \end{pmatrix} $​ 试求其平稳分布：

我们可以令$\pi = (x,y)$​, 那么 $\cases{\frac{1}{2}x+\frac{1}{4}y = x\\frac{1}{2}x+\frac{3}{4}y = y}$ 解得$y=2x$，又要满足平稳分布的行和为1，所以解为：$(\frac{1}{3},\frac{2}{3})$

可约与不可约

如果从状态x可以通过有限步转移到达状态y,并且从状态y可以通过有限步转移到达x，那么称状态x与y是连通的。如果马氏链中任意两个状态都是连通的，那么称该马氏链是不可约的

• 马氏链中任意两个状态都是联通的，那么就意味着存在一个n使得矩阵$\boldsymbol P^{(n)}$ 中任意一个元素都大于0
• 如果一张图是强连通的，那么它一定是不可约的，否则这个图所对应的马氏链是可约的

比如对于这张图，马氏链是可月的，因为对于状态2，他没有出边，因此它无法通过有限步到达其他状态。因此状态2与其他状态并不连通，因此该马尔科夫链是可约的

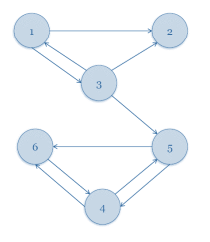
反周期

状态x的周期$dx$ 是集合${n|(P^n){x,x}>0}$的最大公约数，特别地，如果$\forall n\geq 1,(\boldsymbol P^{(n)})_{x,x}=0$,那么$d_x=\infty$ 。而如果一个马氏链所有的状态的周期都为1，则称这个马氏链是反周期的

比如说对于这张图，对于每一个状态其集合都为${2,4,6\cdots}$ 其最大公约数为2，因此这个马氏链是周期的。

例题

1

给定一个转移矩阵 $P$ 和状态向量$\pi$

$$\boldsymbol P = \begin{pmatrix}0.5&0.5\\0.25&0.75\end{pmatrix}&\pi = \begin{pmatrix}1\\0\end{pmatrix}$$

• 证明 $\pi P^n$ 的结果接近一个常数向量

这个常数向量，就是平稳分布。

我们令 $\pi P^n = (x{(n,1)},x{(n,2)})$，那么，对于$n\geq 1$, 我们有：

$$x_{(n,1)} = \frac{1}{2}x_{(n-1,1)} +\frac{1}{4}x_{(n-1,2)}\\ x_{(n,2)} = \frac{1}{2}x_{(n-1,1)} +\frac{3}{4}x_{(n-1,2)}\\$$

由于状态向量$\pi$ 的向量和一定为1，因此 $x{(n-1,2)}=1-x{(n-1,1)}$ ,带入得到：

$$\begin{align} x_{(n,1)} &= \frac{1}{2}x_{(n-1,1)}+\frac{1}{4}(1-x_{(n-1,1)})\\~\\ &=\frac{1}{4}x_{(n-1,1)} +\frac{1}{4} \end{align}$$

这是一个很简单的一阶递推

$$(x_{(n,1)}-\frac{1}{3})=\frac{1}{4}(x_{(n-1,1)}-\frac{1}{3})$$

解得：

$$x_{(n,1)} = \frac{2}{3}\times (\frac{1}{4})^n+\frac{1}{3},n\geq 1$$

当$n\rightarrow \infty$ 时，$x{(n,1)}=\frac{1}{3}$ ，进而可以知道 $x{(n,2)}= \frac{2}{3}$

2

对于一个转移概率矩阵为 $\boldsymbol P$ 的马氏链

$$\boldsymbol P = \begin{pmatrix}0.5&0.5\\p&1-p\end{pmatrix}\\$$

已知实验多次之后，转移概率矩阵对应的马氏链停在状态1的概率大约为 $20\%$, 停在状态2的概率为$80\%$ ，p为未知参数

1. 计算未知参数$p$ 的合理估计值，并给出解释

首先，根据题意是我们知道最终的平稳分布 $(0.2,0.8)$ ，又 $\pi \boldsymbol P = \pi $ ，可知 $0.1+0.8p = 0.2~~p=\frac{1}{8}$

1. 这个马氏链是否可约，是否反周期？

是否可约呢？我们看到这边只有两个状态，两个状态是相互联通的，因此是不可约的。

如图：

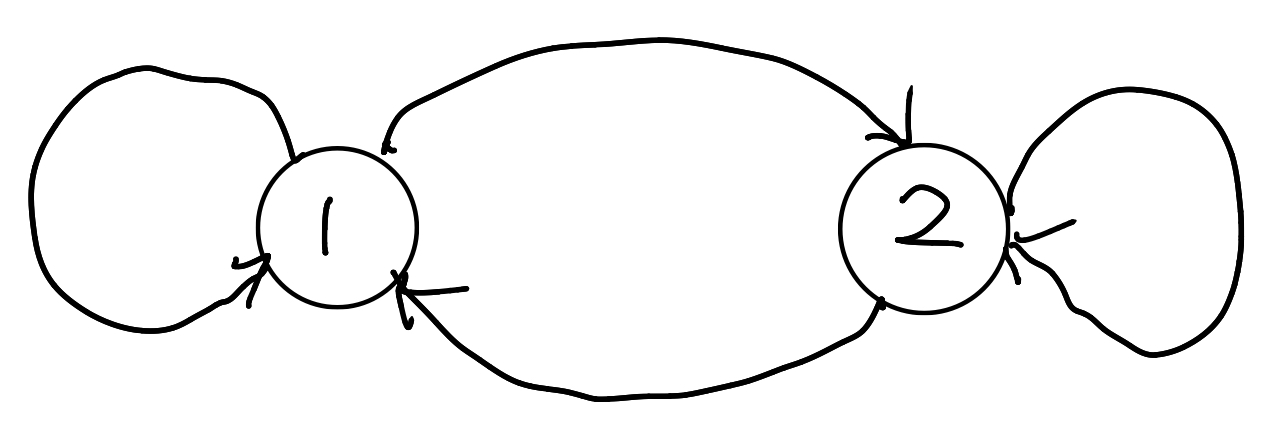
那么是否反周期呢？我们看到，状态1、2的集合为：${1,2\cdots}$ ，其最大公约数都是1，因此这个马氏链是反周期的。

3

• 对于7.5
  • 状态1和状态2都是相互连通的，因此是不可约的
  • 状态1的集合为 ${1,2,\cdots}$ ，状态2的集合为 ${2,3,4\cdots}$ ，两者最大公约数都是1，周期都是1，因此是反周期的
• 对于7.6
  • 一共有4个状态，所有状态都是连通的，因此是不可约的
  • 四个状态，每个状态的集合都是 ${2,4,6,\cdots}$ ，最大公约数都是2，因此是非反周期(周期)的

Page Rank