线性回归分析——PartII
为什么我们一开始不讲矩阵呢?这是因为如果一上来就研究多元线性回归,就会忽略掉很多细节,而且还听不懂
线性回归的模型与假设
多元线性回归就是多个x,其线性回归模型为:
y为响应变量/因变量,为一个随机变量;
x为协变量/自变量,通常假定是确定性的变量
$\beta_0,\beta_1\cdots,\beta_p $是$p+1$个未知参数:
$\varepsilon$为随机误差,并假定:$\cases{E(\varepsilon) = 0\~\Var(\varepsilon) = \sigma^2}$
那么,对于n组观测数据,$(x{i1},x{i2},\cdots,x_{ip},y_i)$,我们可以写出回归方程模型:
对于这些方程,我们可以将其抽象出来形成矩阵、向量的形式
吗线性回归模型的矩阵形式为:
我们看到,用矩阵的方式来表示模型,会比较简洁。
那么,我们要做的就是估计参数向量$\boldsymbol{\beta}$ ,带入模型,这样就可以预测出$\hat y$
线性回归的基本假定
为了便于参数估计,需要对回归方程进行一些假设:
- 关于设计矩阵$\boldsymbol X$
- 它是确定性变量,不是随机变量。在预测的时候,是给定确定的x的条件下去做的预测
- 要求$rank(\boldsymbol{X}) = p+1<n$,这表明了这是个列满秩的矩阵,每一维都不能被其他特征线性表出,每一列的自变量之间不相关。样本量应大于自变量的个数,$\boldsymbol X$是一个满秩矩阵
- 关于随机误差是零均值且等方差的
- $E(\varepsilon_i) =0,i=1,2\cdots,n$ 表示没有系统误差
- $Cov(\varepsilon_i,\varepsilon_j) = \cases{\sigma^2,i=j\0,i\neq j},i,j = 1,2\cdots,n$ 表明随机在不同的样本点之间是不相关的(在正态假定下即独立的),不存在序列相关,并且有相同的精度。只有自身和自身存在协方差(等于方差)
这个条件常被称为高斯-马尔可夫条件
- 假定随机误差服从正态分布
即:$\cases{\varepsilon_i\sim N(0,\sigma^2),i=1,2\cdots,n\~\\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n\text{相互独立}}$
在这个假设下,随机误差向量服从:
即每一维的误差都来自一个正态分布。
$\boldsymbol y$ 分为前后两部分,前面是确定性的,而后半部分$\boldsymbol\varepsilon$ 是随机性的,又 $X$也是服从正态分布的,因此等价于假定因变量$\boldsymbol y$ 服从n维正态分布,其期望向量和协方差矩阵分别为:
线性回归模型的参数估计
最小二乘估计
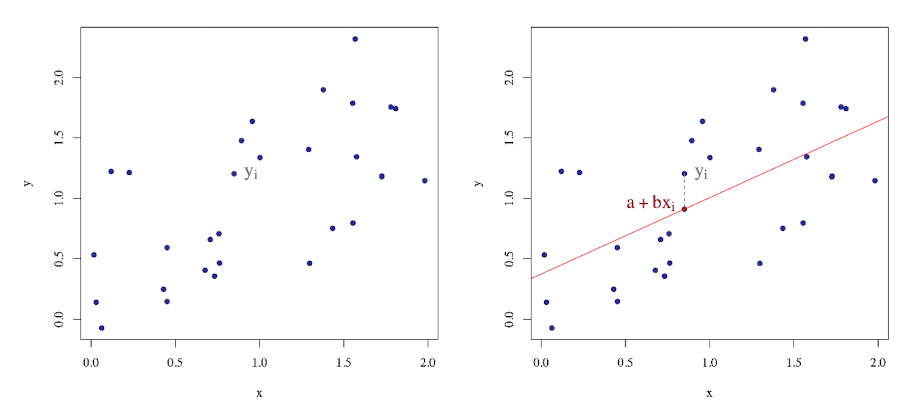
根据这张图我们可以定义离差,也就是实际观测值和估计值的差,即 $y_i-\boldsymbol x_i\boldsymbol \beta$
由此我们可以给出最小二乘估计:通过最小化离差平方和而得到的估计方法
对于线性模型,离差平方和可以定义为:
最小二乘估计为:
这其实是一个数,即行向量乘以列向量,我们可以这样改写上式:
我们要发现$\boldsymbol {y’X\beta}$和$\boldsymbol{\beta’X’y}$ 都是一个数因此可以合并同类项
这样写好以后,相当于一个$\boldsymbol\beta$ 的二次函数,我们可以通过对其求导来找到$\min \boldsymbol \beta$
补充
对于一个向量,我们怎么求其最小值呢,在这里我们补充一些求导的公式:
对于一个 p 维向量 $\boldsymbol x = (x_1,x_2\cdots,x_p)’$
- 线性函数求导:对于任意常向量 $\boldsymbol a = (a_1,a_2\cdots,a_p)’$, 我们有:
- 二次型求导:对于任意$p\times p$ 常值矩阵 $\boldsymbol B$ 我们有:
特别地,若 $\boldsymbol B$ 是一个对称矩阵,那么
具体计算方法
我们用 $Q(\boldsymbol \beta)$ 关于$\boldsymbol \beta$ 求导,可得:
令 $\frac{\partial Q(\boldsymbol \beta)}{\partial \boldsymbol \beta}=0$ 可得:
基于假设(1),$\boldsymbol {X’X}$ 是满秩的,因此 $(\boldsymbol{X’X})^{-1}$ 存在,由此,最小二乘估计为:
说明:
- 根据上式可知,在最小二乘估计$ \boldsymbol{\hat \beta}$ 时,需要$(\boldsymbol{X’X})^{-1}$ 必须存在。也就是说,$(\boldsymbol{X’X})$是一非奇异矩阵,即$\left| {\boldsymbol{X’X}} \right |\neq 0$
- 由线性代数可知 ,$rank(\boldsymbol X)\geq rank(\boldsymbol{X’X})$, 如果$\boldsymbol{X’X}$ 为 p+1阶满秩矩阵,也就是说 $rank(\boldsymbol{X’X})=p+1$,那么$rank(\boldsymbol X)\geq p+1$
- 另一方面,设计矩阵$\boldsymbol X$ 为 $n\times (p+1)$ 阶矩阵,于是应用 $n\geq (p+1)$ 这表明了采用最小二乘法估计方法求解线性回归的未知参数,样本量必须不少于模型的参数个数
拟合值
求得 $\boldsymbol {\hat\beta}_{LS}$之后,我们可以定义回归值或者拟合值为:
其中,$\hat y_i = \boldsymbol x_i’\boldsymbol{\hat\beta} ,~~i=1,2\cdots,n$
我们将 $\boldsymbol {\hat\beta}$ 用上面求得的最小二乘估计带入,得到:
矩阵 $\boldsymbol {X(X’X)^{-1}X’}$ : 将观测值$\boldsymbol y$ 变换为 $\boldsymbol {\hat y}$ ,从形式上来看,就是给$\boldsymbol y$ 戴上了一顶帽子 $\hat ~$ ,因为形象地称矩阵 $\boldsymbol{X(X’X)^{-1}X’}$ 为帽子矩阵,记为$\boldsymbol H$
于是: $\boldsymbol{\hat y} = \boldsymbol {Hy} $
帽子矩阵的性质
帽子矩阵 $\boldsymbol H = \boldsymbol {X(X’X)^{-1}X’}$ 具有以下的一些性质:
$\boldsymbol H$ 是n阶对称矩阵
$\boldsymbol H$ 是幂等矩阵,即$\boldsymbol H =\boldsymbol H^2$
$\boldsymbol H$ 的迹为 $p+1$,即 $tr(\boldsymbol H)=p+1$
证明1:
由于$\boldsymbol H$ 的转置矩阵等于$\boldsymbol H$ ,所以$\boldsymbol H$ 是对称的
证明2:
因此$\boldsymbol H$是幂等矩阵
证明3:
易知$\boldsymbol{X’X}$是一个 $(p+1)\times(p+1)$ 的满秩矩阵。于是我们计算$\boldsymbol H$ 的迹,即:
我们要知道矩阵迹的运算性质:多个矩阵相乘得到的方阵的迹,和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的,即:
残差
说完了拟合值,我们聚焦到最后一个部分——残差
我们把残差定义为拟合值和真实值之间的距离
也可以写为 :
几何上的关系:回归值 $\boldsymbol {\hat y}$与残差$\boldsymbol e$ 垂直,即:
然后,我们写出残差的协方差矩阵为:
由此,我们可以构造误差项方差$\sigma^2$ 的估计,用残差去估算即:
极大似然估计
现在我们介绍第二种方法——极大似然估计。$\boldsymbol y$ 是服从多元正态分布的,即:
因此 $\boldsymbol y$ 的联合密度函数为:
参数 $( \beta,\sigma ^2) $的 似然函数为
进而我们给出极大似然估计 :
具体计算方法
对数似然函数分布关于$\boldsymbol \beta$和和$\sigma^2$求导,即
反解得到:
说明:
$\boldsymbol{\hat\beta}{ML}=\boldsymbol{\hat\beta}{LS}$ ,因此,我们不用写下标了,一般记为 $\boldsymbol{\hat\beta} = (\boldsymbol{X’X})^{-1}\boldsymbol{X}’\boldsymbol y$
$\hat\sigma^2_{ML}$ 不是一个无偏估计,但是一个相合估计
参数估计性质
概率论 关于矩阵的期望方差复习。假设$\boldsymbol {x,y}$是n维随机变量。对任意一个$m\times n$ 维常矩阵 $\boldsymbol A$ 和一个$m’\times n$ 维常矩阵$\boldsymbol B$,以及一个m维向量$\boldsymbol c$
- $E(\boldsymbol {Ax+c})=\boldsymbol{A}E(\boldsymbol {x})+\boldsymbol c$
- $Var(\boldsymbol{Ax+c})=\boldsymbol A\text{Var(x)}A’$
- $Cov(\boldsymbol{Ax,By})=\boldsymbol A Cov(\boldsymbol{x,y})\boldsymbol B’$
最小二乘估计的性质
最小二乘估计 $\boldsymbol{\hat\beta}=(\boldsymbol{X’X})^{-1}\boldsymbol{X’y}$ 那么$\boldsymbol{\hat\beta}$ 满足:
- $E(\boldsymbol{\hat\beta})=\boldsymbol{\beta}$, 即$\boldsymbol{\hat\beta}$是$\boldsymbol \beta$ 的无偏估计
- $Var(\boldsymbol{\hat\beta})=\sigma^2(\boldsymbol{X’X})^{-1}$
证明1:计算$E(\boldsymbol {\hat\beta})$
证明2:计算$Var(\boldsymbol{\hat\beta})$
最小二乘估计$\boldsymbol {\hat\beta}$与残差$\boldsymbol e$ 的关系
最小二乘估计$\boldsymbol \beta$与残差$\boldsymbol e$ 线性不相关,即
之前我们说到,最小二乘估计$\boldsymbol {\hat\beta}$与残差$\boldsymbol e$ 在数学层面是垂直的。那么反映在统计中,就是线性无关的。也就是他们两的协方差等于0
说明:特别地,在正态分布的假定下,最小二乘估计$\boldsymbol{\hat\beta}$与残差$\boldsymbol e$ 独立。基于此,最小二乘估计$\boldsymbol {\hat\beta}$ 与残差平方和 $SS_E=\boldsymbol{e’e}$独立
证明:
根据上面所说的协方差的性质,又知道帽子矩阵$\boldsymbol H = \boldsymbol {X(X’X)^{-1}X’}$ ,以及$\text{Cov}(\boldsymbol{y,y})=\sigma^2$,原式可化简为:
因为 $(\boldsymbol{X’X})^{-1}=\boldsymbol X^{-1}{\boldsymbol X’}^{-1}$, 所以:$\boldsymbol{I}_n-\boldsymbol{X(X’X)^{-1}X’}=0$
因此$\text{Cov}=0$ ,得证
中心化和标准化
中心化
矩阵知识补充
假定$\boldsymbol A$ 是$m\times m$ 可逆矩阵,$\boldsymbol B$是 $m\times n$矩阵,$\boldsymbol C$ 是$n\times m$ 矩阵,$\boldsymbol D$是$n\times n$ 矩阵。如果$\boldsymbol D-\boldsymbol{CA^{-1}B}$ 是$n\times n$ 可逆矩阵,那么:
其中,
中心化步骤
所谓中心化,就是把矩阵的中心拉到0 ,我们用$x_{ij}^,y_i^,\boldsymbol X^*$ 来表示中心化后的数据:
令
其中,$\boldsymbol xj^*=(x{1j}^,\cdots,x_{nj}^)’$
中心化前后的关系
标准化前,原数据集为:
因为根据模型,$\boldsymbol X$的第一列都是1,所以在上面做一个拼接
最小二乘估计为:
其中 $\boldsymbol A_o=(\boldsymbol X_o’\boldsymbol X_o-n^{-1}\boldsymbol X_o’\boldsymbol 1_n\boldsymbol 1_n’\boldsymbol X_o)^{-1}$
对于中心化的数据,我们有相似的:
其中 $\boldsymbol A_c=(\boldsymbol X_c’\boldsymbol X_c-n^{-1}\boldsymbol X_c’\boldsymbol 1_n\boldsymbol 1_n’\boldsymbol X_c)^{-1}$
中心化的因变量与为中心化的因变量之间的关系:
其中 $\boldsymbol H_{1n} = \boldsymbol 1_n(\boldsymbol 1_n’\boldsymbol1_n)^{-1}\boldsymbol1_n’$是对称幂等矩阵, 即一个$\boldsymbol 1_n$张成的帽子矩阵
中心化的自变量与未中心化的自变量之间的关系:
而且 $\boldsymbol1n$向量和它张成的空间的补空间$(\boldsymbol I_n-\boldsymbol H{1n})$ 是垂直的,可以有如下证明
然后我们要找$\boldsymbol A_c$和$\boldsymbol A_o$的关系
因为前面的$(\boldsymbol In-\boldsymbol H{1n})$是幂等且对称的矩阵
后面 $(\boldsymbol Xo’(\boldsymbol I_n-\boldsymbol H{1n})\boldsymbol Xo)^{-1} = \boldsymbol A_0$中有$1_n’(\boldsymbol I_n-\boldsymbol H{1n})$ 因此直接等于0
因此:
已知经验回归方程为:
我们把中心化的数据用到最小二乘估计模型中,即估算回归常数和回归系数:
估计 $\hat\beta_{\text{c,intercept}}$
对于回归常数,我们代入数据
我们发现,括号中的后两项都有$\boldsymbol 1n’\boldsymbol X_c’$ ,也就是 $\boldsymbol 1_n’(\boldsymbol I_n-\boldsymbol H{1n})\boldsymbol X_o$ .我们刚刚证明了这是垂直的,乘积为0
因此:
估计$\hat\beta_{\text{c,slope}}$
因为$\boldsymbol 1n$ 是 竖向量,因此 $\boldsymbol1_n’\boldsymbol1_n$ 是一个常数,为 $\frac{1}{n}$因此,我们有 $\boldsymbol H{1n} = \boldsymbol 1_n(\boldsymbol 1_n’\boldsymbol1_n)^{-1}\boldsymbol1_n’ =\frac{1}{n}\boldsymbol (\boldsymbol 1_n\boldsymbol 1_n’) $
因此
采用了中心化的数据得到的经验回归方程为:
也就是说,$\beta_1,\beta_2\cdots,\beta_p$的估计是不会变的
标准化
步骤
其中,$L_{jj}$是自变量 $x_j$ 的离差平方和,即:
而$L_{yy}$是因变量y的离差平方和,即
进而我们可以定义向量$\boldsymbol y^{**}$和矩阵$\boldsymbol X_s$
我们从$x{ij}^*$的定义可以知道,其实就是中心化的$x{ij}$ ,因此$\boldsymbol X_s$可以被写为:
其中,$\boldsymbol L=diag{\frac{1}{\sqrt{L{11}}},\cdots,\frac{1}{\sqrt{L{pp}}}}$
参数估计
标准化后的最小二重估计为:
回归系数为:
那么$\boldsymbol{\hat\beta}{\text{s,slope}} $ 和 $\boldsymbol{\hat\beta}{\text{c,slope}} $ 的关系又如何呢?我们先把$\boldsymbol{\hat\beta}_{\text{c,slope}} $化简成 $\boldsymbol X_c$的表达式
注意: $\boldsymbol {\hat\beta_{\text{c,slope}}} $ 还不是最终形态,我们可以这样来化简:
因为上面证过了,$\boldsymbol A_c$展开后后面一项等于0,因此:
因此:
其中每一个分量为:
显著性检验
概述
我们做了这么多参数估计,现在我们进一步判断因变量y和自变量$x_1,x_2\cdots,x_p$ 之间是否存在显著的线性关系。
因此,我们可以采用F检验和t检验这两种统计检验方法:
- F检验: 用于检验回归方程的显著性
- t检验:用于检验回归系数的显著性
我们之前学过,在一元线性回归模型中,F检验(研究方差分析)和t检验(枢轴量法)、相关系数这三类检验是等价的
在多元线性回归模型中,F检验和t检验就不等价了。而且在多元线性回归中,两个变量之间的相关性是很难定义的,因为会受到其他变量的影响
F检验
F检验是检验回归方程的显著性。对多元线性回归方程的显著性检验是要看自变量 $x_1,x_2\cdots,x_p$ 从整体上对因变量y是否有明显的影响
原假设为
备择假设为:
如果$H_0$ 为真,则表明因变量y与$x_1,x_2\cdots,x_p$ 之间的关系用线性回归模型来刻画是不合适的
检验过程
离差平方和:
我们记为
拟合值: $\hat y_i = \boldsymbol x_i’\boldsymbol {\hat\beta}$
偏差: $e_i = y_i-\hat y_i$