数据科学算法ch11-整数规划
引入
这章我们来学习离散变量的优化问题。这些问题的描述非常简单,但是由于”组合爆炸”的原因,导致求解此类问题的最优解变得非常困难。典型的问题有:旅行商问题(TSP),集合覆盖问题(SCP)等。这里给出几例
旅行商问题
给定一组城市以及每两个城市间的旅行成本(或距离),旅行商问题(TSP)旨在:在经过每个城市一次的情况下最后回到出发的城市,应该如何选择行进路线以使总行程最短?
即输入:包含n个点的几何,以及两两间的成本
输出:如果遍访所有顶点,对 对称TSP问题 的可行解决方案为$\frac{(n-1)!}2$
目标函数:最小化旅行成本(或距离)的大小
那么TSP就可以定义在一个无向图上:$G=(V,E)$,其中$V$为顶点集合 $E$为边的集合,且每条边的成本为 $c_{jj}$

约束的第一个式子:保证从一个城市出发只能去一个城市
约束的第二个式子:保证每个城市只能被访问一次
约束的第三个式子:保证只有n个顶点构成的一个环,从而回到出发的城市。如果地图上有两个环,就不是TSP问题的解
集合覆盖问题(SCP)
输入:
- 全集 $U = {u_1,u_2,\cdots,u_n}$
- 子集簇 $S = {S_i|S_i\subseteq U ,i\in [1,\cdots,m]}$
- 成本 $C = {c_1,\cdots,c_m}$
目标:找到一个指标集 $I\in {1,\cdots,m}$ ,使得$\sum{i\in I}c_i$ 最小且满足 $\bigcup{i\in I}S_i = U$
集合覆盖问题具有广泛的应用:
- 全覆盖和最大覆盖
- 顶点覆盖
- 信息传播
- 文本摘要
Fiver 游戏
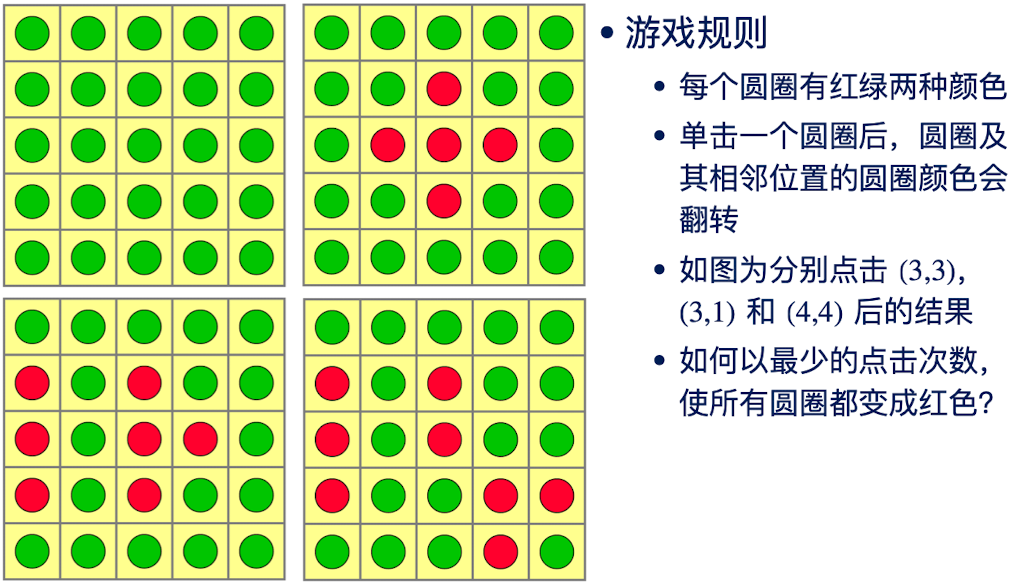
问题定义:我们注意到,同一个圆圈被点击两次,又恢复了原样,若一个圆圈为红色,这个圆圈及其周围4个圆圈总共被点击的次数一定为一个奇数。
因此我们可以定义:
该问题可以建模为:
然而,这并不是一个规划问题,因为其中的约束条件并不是线性的。我们知道最坏的条件就是一个圆圈被点击了五次变为红色(自己+左右上下),那通过引入一个自由变量$y_{ij}$, 令其取值为$[0,2]$,我们就可以将这个问题转化成一个整数规划的问题:
这里,$y{ij}=0$,就是取1的情况;$y{ij}=1$ 就是取3的情况;$y_{ij}=2$ ,就是填5的情况。也就是覆盖了所有情境,将自然语言转换成了优化条件
以上举的三个例子,最后都转换成了线性整数规划,其要求就是输入和输出都是线性函数,可行解是所有满足这些线性等式(不等式),且要满足完整性(即整数),接下来详细来介绍一下:
整数规划
线性整数规划化在我们初中的时候就已经学过了,就是一类需要用画图解决的应用题。但是难点就在于如何建模,使得自然语言转换成约束条件。
线性整数规划类型可以分成下面三种:
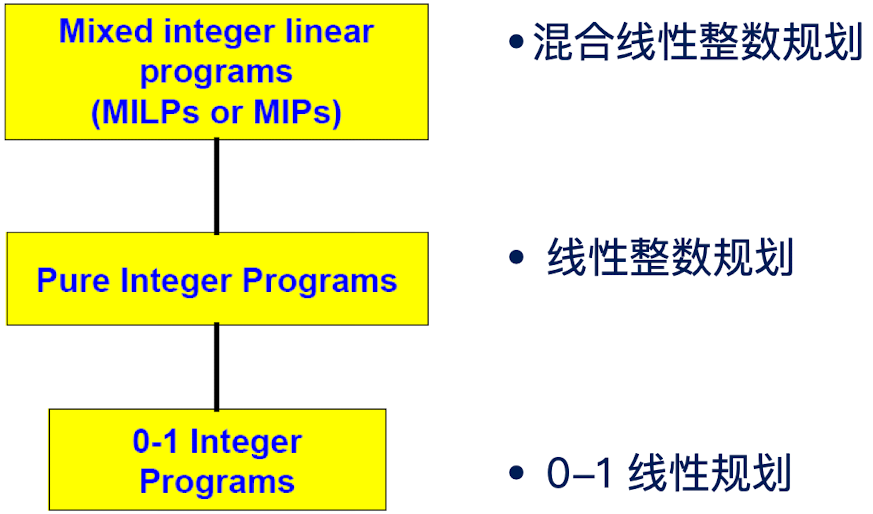
第一种 混合线性整数规划。在这章中没有涉及,没有特别有效的方法来解决。
第二种 线性整数规划,即目标函数是线性的,约束是线性条件,解的类型是整数
第三种 0-1线性规划,是线性整数规划的一种特殊类型,比如Fiver问题、TSP问题。其特点就是变量的类型都是布尔型。
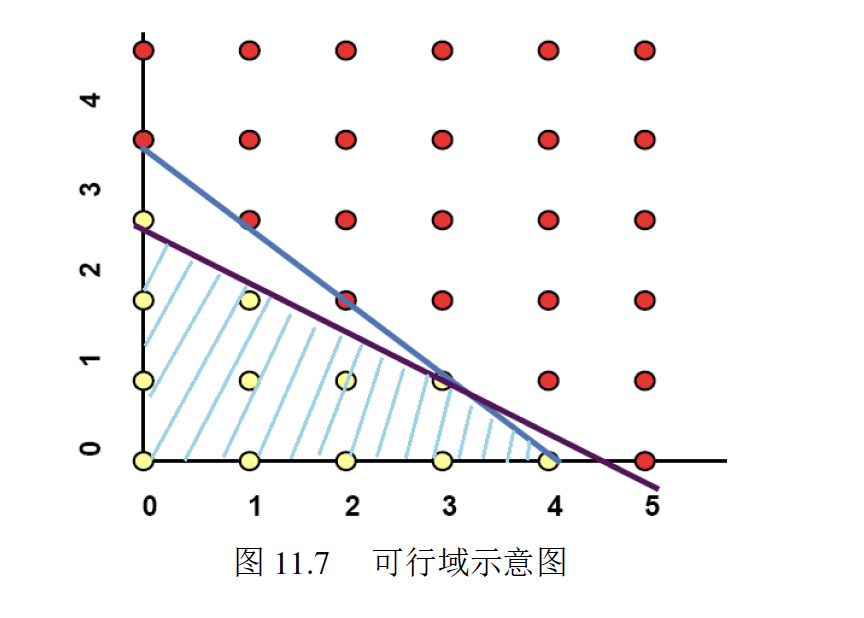
比如说这里有一个整数规划的问题:
其可行域就是由空心点组成的集合:
分支定界法
上面这个整数规划的例子,只有两个决策变量,即使每个可行解都试一遍,也很快就能得到该整数规划问题的解,那么如果有很多决策变量的情况该怎么办呢?
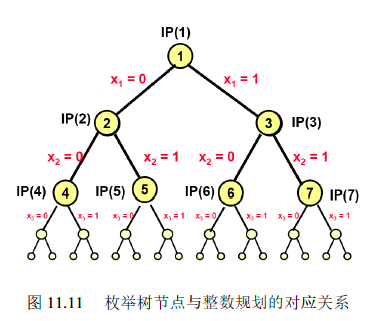
我们要学习:枚举树
比如下面这个例子
如果我们一一枚举,那么所有可能的取值有$2^4$种,但是在现实生活中,决策变量的数量可能为n,如果一个一个去,那么可行域的大小就可能是$2^n$ 。因此,如何有效地遍历整个可行域成为一个关键的问题。
通常,我们可以利用枚举树把整个可行域迭代地分割为越来越小的子集,每个子集称为一个分支。
在枚举树中,每个节点对应一个整数规划的问题,其中根节点是原始的整数规划问题,每个节点的孩子,是在父亲节点对应的整数规划问题上,通过固定某个决策变量的取值来得到一个新的整数规划问题。
以上面这个整数规划问题为例,那么$IP(1)$ 对应的整数规划问题是:
那么根节点的两个孩子节点$IP(2)$和$IP(3)$ 分别为如下的整数规划问题:
以此类推,每个节点都有两个孩子节点,对于整数规划问题$IP(1)$ ,可以构建下图所示的枚举树
松弛和定界
但这样也并不能解决变量一多以后的运算问题,如果能够去掉一些明显不会称为最优解的分支,那么求解整数规划的问题会变得更为高效。
比如说对于上面这棵枚举树中的 $IP(4)$和$IP(7)$.
关于$IP(4)$ ,我们的整数规划的定义如下:
我们已经知道了它的最优解,那么$IP(4)$ 的所有子孙结点都不需要在进行计算,因为$IP(4)$的最优解一定是其子孙结点的一个上界。
我们需要把$IP(4)$中的整数约束去掉,问题就转化为如下的一个线性规划问题,这样的目的是,LP问题的最优解一定是IP问题的最优解的上界。
记作$LP(4)$:
我们很容易发现对于线性规划问题 $LP(4)$ ,很容易发现它的最优解是 $x_1=0,x_2=0,x_3=1,x_4=1,z=24$ .
关于$IP(7)$ ,我们将其转化为线性规划问题:
同样可以发现其最优解为:$x1=1,x_2=1,x_3=0,x_4=0,z{IP(7)}=26$ .
如果$IP(8)$的最优解不会超过$IP(7)$ ,那么包括节点$IP(8)$ 和它的自己孙节点也都不需要再进行计算了。
重点:
整数规划的松弛线性规划问题的解释整数规划问题解的上界。如果$IP(8)$ 对应的松弛线性规划问题$LP(8)$ 的解都不超过$IP(7)$,即:
因此,通过整数规划问题的松弛找到了响应节点整数最优解的上界
分支定界算法
现在我们来对枚举树进行剪枝规则
- 已经找到了某个节点的最优解,该节点的所有子孙结点都不需要再解。因此其所有的子孙结点都可以从枚举树中删除
- 如果已知枚举树中某个节点的最优解,而当前节点的松弛线性规划问题的最优解都比已知的最优解要小,那么当前结点对应的整数规划问题不可能成为最优解,当前节点及其子孙结点都不用再解、因此当前节点及其子孙结点都可以直接从枚举树中删除
- 如果当前结点对应的松弛线性规划问题没有可行解,那么当前节点及其子孙结点都不可能存在可行解。因此可以直接从枚举树中删除。
我们可以用一下伪代码概括

算法中的 active结点,意味着这些节点对应的整数规划问题可能是该整数规划的最优解。只要枚举树中还有active结点,分支定界算法就要继续执行,直到没有为止
算法记录当前位置所发现的最优解,记为$Z_I$ ,初始值为$-\infty$ 。算法基于线性规划问题$LP(j)$的最优解$x(j)$来判断:
- 第一种情形:线性规划问题$LP(j)$无解,则枚举树中的节点$IP(j)$及其子孙结点会被剪枝
- 第二种情形:如果$Z_{LP}(j)\leq Z_I$ ,则枚举树中的节点$IP(j)$及其子孙结点会被剪枝
第三种情形:如果$Z{LP}(j)>Z_I$ ,且$x(j)$为整数解,即$x(j)$也是$IP(j)$ 的可行解,算法找到一个比当前最优解还要更优的一个可行整数解$x(j)$, 因此当前最优解$Z_I$ 更新为$Z{LP}(j)=Z_{IP}(j)$,并将枚举树中的节点$IP(j)$ 及其子节点全部剪枝
第四种情形:如果$Z_{LP}(j)>Z_I$,但是$x(j)$为非整数解,即 $x(j)$ 不是$IP(j)$ 的可行解,算法无法判断节点$IP(j)$的子孙结点中是否存在更优的解,因此将节点$IP(j)$的孩子标记为active结点
例子
我们还是用刚才的整数规划例子:
迭代1
初始状态$IP(1)$的松弛线性规划$LP(1)$作为枚举树根节点,标记为active,当前最优解$Z_I=-\infty$
通过解决线性规划问题$LP(1)$,得到$LP(1)$的最优解为:
(关于如何解决线性规划问题,可以通过python的pulp包来求解)
因为$Z_{LP}(1)>Z_I$ ,且$x(1)$为非整数解,即$x(1)$不是$IP(1)$的可行解,属于第4种情形,那么将$IP(1)$标记为inactive,并将$IP(1)$的两个孩子结点$IP(2)$和$IP(3)$ 标记为active结点
迭代2
迭代2选择了结点$IP(2)$,如图所示
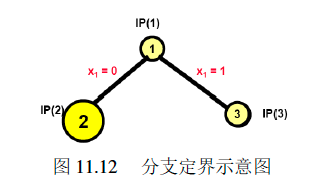
这里枚举树中的结点$IP(2)$ 的松弛线性规划问题为$LP(2)$。通过解决线性规划问题$LP(2)$可以得到最优解:
由于$Z_{LP(2)}>Z_I$ ,且$x(2)$ 为非整数解,即$x(2)$ 不是$IP(2)$ 的可行解,属于第4种情形。
分支定界算法将$IP(2)$标记为inactive,并将$IP(2)$ 的两个孩子节点$IP(4)$和$IP(5)$ 标记为active结点
迭代3
第三次迭代选择$IP(3)$,如图所示:
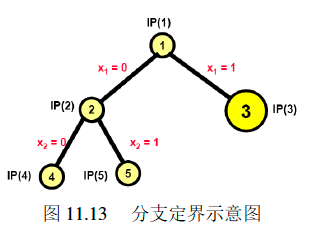
这里枚举树中的结点$IP(3)$ 的松弛线性规划问题为$LP(3)$。通过解决线性规划问题$LP(3)$可以得到最优解:
由于$Z_{LP(3)}>Z_I$ ,且$x(3)$ 为非整数解,即$x(3)$ 不是$IP(3)$ 的可行解,属于第4种情形。
分支定界算法将$IP(3)$标记为inactive,并将$IP(3)$ 的两个孩子节点$IP(6)$和$IP(7)$ 标记为active结点
迭代4
第四次选择了$IP(4)$,如下图:
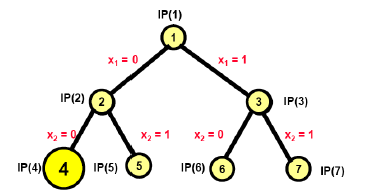
这里枚举树中的结点$IP(4)$ 的松弛线性规划问题为$LP(4)$。通过解决线性规划问题$LP(4)$可以得到最优解:
由于$Z_{LP(4)}>Z_I$ ,且$x(4)$ 是整数解,即$x(4)$ 是$IP(4)$ 的可行解,属于第3种情形。
因此,分支定界算法将当前的最优解更新为:$ZI=Z{LP(4)}=Z_{IP(4)}$,并进一步将$IP(4)$所有的孩子结点剪枝
迭代5
第5次迭代中,选择active结点$IP(5)$,如下图:
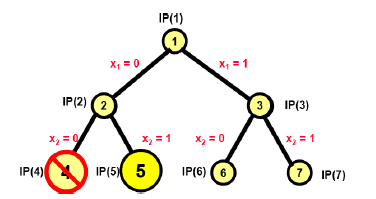
这里枚举树中的结点$IP(5)$ 的松弛线性规划问题为$LP(5)$。通过解决线性规划问题$LP(5)$可以得到最优解:
由于$Z_{LP(5)}>Z_I$ ,但$x(5)$ 为非整数解,即$x(5)$ 不是$IP(5)$ 的可行解,属于第4种情形。
分支定界算法将$IP(5)$标记为inactive,并将$IP(5)$ 的两个孩子节点$IP(8)$和$IP(9)$ 标记为active结点
迭代6
选择active节点 $IP(6)$ ,如下图:
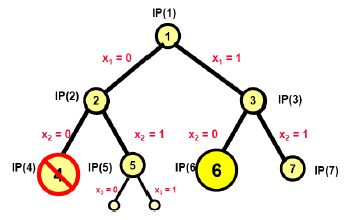
这里枚举树中的结点$IP(6)$ 的松弛线性规划问题为$LP(6)$。通过解决线性规划问题$LP(6)$可以得到最优解:
由于$Z_{LP(6)}>Z_I$ ,但$x(6)$ 为非整数解,即$x(6)$ 不是$IP(6)$ 的可行解,属于第4种情形。
分支定界算法将$IP(6)$标记为inactive,并将$IP(6)$ 的两个孩子节点$IP(10)$和$IP(11)$ 标记为active结点
迭代7
选择active节点 $IP(7)$ ,如下图:
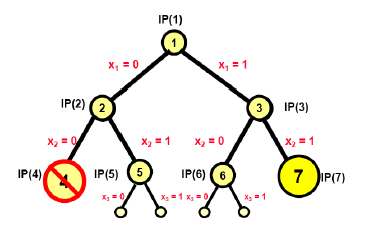
这里枚举树中的结点$IP(7)$ 的松弛线性规划问题为$LP(7)$。通过解决线性规划问题$LP(7)$可以得到最优解:
此时发现$Z{LP}(7)>Z_I$ 且$x(7)$为整数解,因此$x(7)$是$IP(7)$的可行解,属于第3种情形。因此,分支定界算法将当前的最优解更新为:$Z_I=Z{LP}(7)=Z_{IP}(7)$,并进一步将$IP(7)$所有的孩子结点剪枝
迭代8
选择active节点 $IP(8)$ ,如下图:
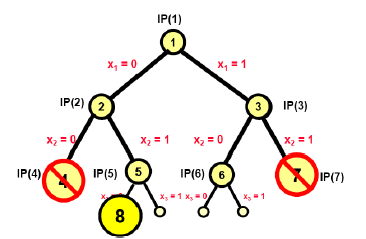
这里枚举树中的结点$IP(8)$ 的松弛线性规划问题为$LP(8)$。通过解决线性规划问题$LP(8)$可以得到最优解:
此时发现$Z_{LP}(8)<Z_I$ ,属于第2种情形,分支定界算法将$IP(8)$标记为Inactive,并将IP(8)的两个孩子结点全部剪枝
迭代9
选择active节点 $IP(9)$ ,如下图:
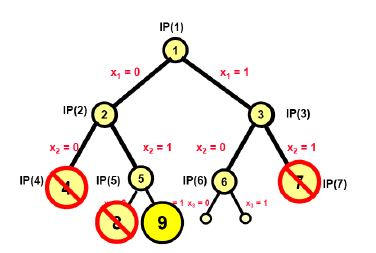
这里枚举树中的结点$IP(9)$ 的松弛线性规划问题为$LP(9)$。通过解决线性规划问题$LP(9)$可以得到最优解:
由于$Z_{LP(9)}<Z_I$ , 属于第2种情形,分支定界算法将$IP(9)$标记为Inactive,并将$IP(9)$的两个孩子结点全部剪枝
迭代10
选择active节点 $IP(9)$ ,如下图:
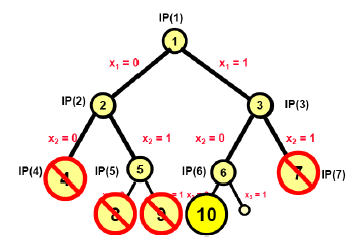
这里枚举树中的结点$IP(10)$ 的松弛线性规划问题为$LP(10)$。通过解决线性规划问题$LP(10)$可以得到最优解:
由于$Z_{LP(9)}<Z_I$ , 属于第2种情形,分支定界算法将$IP(10)$标记为Inactive,并将$IP(10)$的两个孩子结点全部剪枝
迭代11
选择active节点 $IP(11)$ ,如下图:
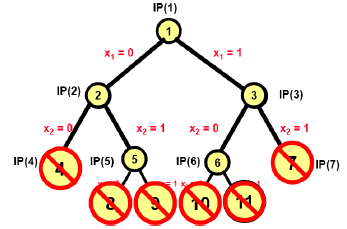
这里枚举树中的结点$IP(11)$ 的松弛线性规划问题为$LP(11)$。通过解决线性规划问题$LP(11)$可以得到最优解:
因此,最终得到的结果是 $Z = 26$
割平面法
找到合适的约束可以大大减低整数规划问题的求解过程,为了找到合适的约束条件,这里先定义有效不等式的概念。
有效不等式
给定一个整数规划问题,一个约束条件可以减小松弛线性规划问题的可行域,但却不减少任何整数的可行解,则称其为有效不等式,有事又被称为割平面或者割
例题
1
将下列条件改成整数规划的约束,保证两个不等式中至少有一个成立
其中 $x_j\geq 0,j=1,\cdots,4$, 并且每一个变量都是整数。
解:
我们可以把这个问题变成0-1整数规划问题,令:
令 $M>0$
则有:
其中 $w={0,1}$
这样, 不管 $w$ 的取值如何,$(1),(2)$ 至少有一个成立