数据科学算法ch12-子模函数

子模函数时边际效用递减规律的形式化表示。在机器学习和人工智能领域，子模函数有着广泛的应用，如文档摘要、信息扩散、传感器布置和图像采集描述等诸多问题

比如说：要在办公楼里面布置无线网络，由于在不同的位置安装无线路由器的效果是不同的，那么在那些地方安装无线路由器能满足上述条件且总花费越低？要知道，部署的无线路由器越多，对提升网络覆盖率的贡献就越低。

又比如说：在大数据时代，日常看到的信息可能是片面零散的，可以采用文本摘要技术来帮助人们解决碎片化阅读的问题。我们的目标是用尽量少的句子来覆盖用户感兴趣的关键词。当选择的句子越来越多，未被包含的关键词就越少，因此选择句子对文本中的关键词覆盖也符合边际效用递减的规律。

上面例子中都设计边际效用递减规律，在数学上这个规律可以被定义为子模函数

子模函数

在了解子模函数前，我们首先了解一下凸函数和凹函数：

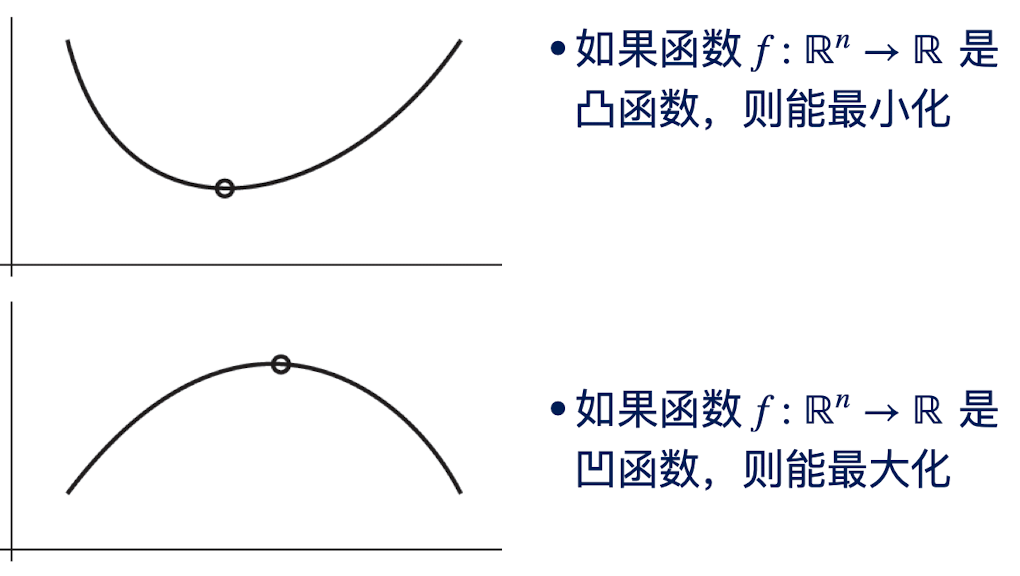
现在我们从凹函数到子模：

对于集合函数$f:{0,1}^n\rightarrow \mathbb R,\forall i,\partial_if(x)=f(x+e_i)-f(x)$ 是非增的，那么$f(x)$就是子模函数

也就是说，从集合中任意调出一个子集来，我们可以将其映射为一个实数，然后这个实数的变化趋势和凹函数是一致的。

但是对于集合函数来讲，单调性并不是说一个大小为5的子集对应的函数的值一定大于一个大小为4的子集。它只大于它自己的大于等于4的子集的函数值。

用集合的话来说：

集合函数： $f:{0,1}^n\rightarrow \mathbb R$ 是子模函数当且仅当对 $\forall A,B\subseteq V$, 以下不等式成立

$$f(A)+f(B)\geq f(A\cap B)+f(A\cup B)$$

子模函数的等价定义

子模函数有两个等价定义：

边际效用递减：

对任意的 $S\subseteq T\subseteq V$ 和 $v\in V \backslash T$

$$f(S\cup \{v\})-f(S)\geq f(T\cup \{v\})-f(T)$$

这实际上就是边际效用递减规律的形式化表述。

• 我们可以把边际效用看做是：$f(S\cup {v})-f(S)$ ，即在集合S中增加元素 $v$ 导致函数值变化。
• 进一步，随着集合$S$ 的不断增大，比如增加到集合T ,那么显然边际效用 $f(T\cup {v})-f(T)$ 是不断减少的。

因此，我们说当 $S\subseteq T$ 的时候，$f(S\cup {v})-f(S)\geq f(T\cup {v})-f(T)$

集合效用递减：

对于任意的$S\subseteq T\subseteq V$ 以及 $C\subseteq V \backslash T$

满足：

$$f(S\cup C)-f(S) \geq f(T\cup C)-f(T)$$

也很容易理解，上面是加一个元素，现在是加一个集合，归根到底就是边际效用递减

子模函数的性质

假设 $f(A)$ 和 $g(A)$ 为任意两个子模函数，则：

1. 对 $\forall a> 0$ ,$af(A)$ 也是一个子模函数
2. $f(A)+g(A)$ 也是一个子模函数
3. $\overline f(A)=f(A^c)$ 也是一个子模函数
4. 对任意固定的 $S\subset U$,$f(A|S)=f(A\cap S)$ 也是一个子模函数
5. 对任意固定的 $S\subset U$ ,$f(A|S^c) = f(A\cup S)-f(S)$ 也是一个子模函数

例题

例题1

给定一个集合$ V$，当$A\subseteq V$ 的时候，有 $f(A)$ 是一个子模函数

a. 证明 $\overline f(A)= f(A^c)$ 是一个子模函数

b. 证明 当$S\subset V,~g(A) = f(A\cap S) $ 是一个子模函数

证明什么函数是一个子模函数，我们一定要从定义入手，也就是 $f(S)+f(T)\geq f(S\cup T)+f(S\cap T)$

比如说a, 我们令 $A = S^c,B=T^c$, 带入到 $f(A)$中，得到

$$f(A)+f(B) \geq f(A\cup B)+f(A\cap B)\\~\\ f(S^c)+f(T^c)\geq f(S^c\cup T^c)+f(S^c\cap T^c)$$

已知：

$$A\cup B = S^c\cup T^c = (S\cap T)^c\\ A\cap B = S^c\cap T^c = (S\cup T)^c\\ f(S\cap T)^c = \overline f(S\cap T)\\ f(S\cup T)^c = \overline f(S\cup T)$$

又：

$$f(S^c) = \overline f(S)\\ f(T^c) = \overline f(T)$$

因此，上式可以化为：

$$\overline f(S)+\overline f(T)\geq \overline f(S\cap T)+\overline f(S\cup T)$$

得证

---

对于b，即：

$$\begin{align} f(A\cap S)+f(B\cap S) &\geq f\bigg((A\cap S)\cup(B\cap S)\bigg)+f\bigg((A\cap S)\cap(B\cap S)\bigg)\\ &\geq f\bigg((A\cup B)\cap S \bigg)+f\bigg( (A\cap B)\cap S \bigg)\\ \end{align}$$

我们令 $S = A\cap S, T = B\cap S$, 那么，根据上式，可知： $g(S)+g(T) \geq g(S\cap T)+g(S\cup T)$

例题2

a. 证明边际效用递减的等价定义

需要分充分性和必要性证明，首先证明必要性

令 $S\subset T$ ，给定集合 $S\cup{V}$ 和 $T$， 如果 $v\notin T$, 根据定义，我们有：

$$f(S\cup\{v\})+f(T)\geq f(S\cup \{v\}\cup T)+f(S\cup\{v\}\cap T)$$

注意到： $f(S\cup{v}\cup T)=f(T\cup{v}),f((S\cup{v})\cap T)=f(S)$

带入上式，有：

$$f(S\cup \{v\})-f(S)\geq f(T\cup\{v\})-f(T)$$

然后，我们来证明充分性

给定两个集合 $S$ 和 $T$ ,令 $T\backslash S = {v_1,v_2\cdots,v_k}$, $T_j = {v_1,\cdots,v_j}$ , 我们令：$A_j = (S\cap T)\cup T_j,B_j = S\cup T_j$ , 我们有：

$$f(A_j\cup{v_{j+1}})-f(A_j)\geq f(B_j\cup{v_{j+1}})-f(B_j),j = 0,\cdots,k-1$$

对上式的$k-1$ 个句子求和，可以得到：

$$f(S)+f(T)\geq f(S\cup T)+f(S\cap T)$$

b. 证明集合效用递减的等价定义

将上面的$v_i$ 换成集合$C$ 即可

例题3

设 $w: N\rightarrow R$ 表示有限集 $N$ 中元素的权重，考虑一个线性函数为：

$$f(S) = \sum_{i\in S}w_i ,\forall S\subseteq N$$

证明这个线性函数是一个子模函数

$$f(S) = \sum_{i\in S} w_i\\ f(T) =\sum_{i\in T} w_i\\ f(S\cup T) = \sum_{i\in {S\cup T}} w_i\\ f(S\cap T) = \sum_{i\in {S\cap T}} w_i\\ f(S\cup T)+f(S\cap T) = \sum_{i\in S\cup T}w_i+\sum_{i\in S\cap T} w_i= \sum_{i\in S}w_i+\sum_{i\in T}w_i-\sum_{i\in S\cap T}+\sum_{i\in S\cap T}=f(S)+f(T)\\$$

满足 子模函数对 $f(S)+f(T)\geq f(S\cup T)+f(S\cap T)$ 的定义，因此这个函数是一个子模函数

集合覆盖

首先给出覆盖及其相关定义：

集合覆盖

设A是非空集，C是集合A的非空子集组成的集合，即$C={A\alpha|A\alpha\in A,A_\alpha\neq \empty}$ ，C是集合A的覆盖，若C满足：

$$\bigcup_{A_\alpha\in C}A_{\alpha} = A$$

最小全覆盖问题

令U为一有限集，$\mathcal S = {s_1,\cdots,s_n}$ 为 由U的n个子集构成的集族，全覆盖问题是找到$\mathcal S$最小的子集盖 集合U

简单来说，就是找到最小的 句子集合包含所有的单词

k-最大覆盖问题

令$U$为一有限集，$\mathcal S={s_1,s_2\cdots,s_n}$ 为由$U$的n个子集构成的集族，给定正整数k，最大子覆盖问题就是从$\mathcal S$ 中找到k个子集，使得这k个子集覆盖集合$U$中最多的元素

简单来说，找到k个句子使得其包含的单词数量最多

例题

比如话务验业务技能全集$U={a,b,c,d,e,f,g,h,i,j,k,l}$，现在考虑有7名候选话务员的集合$S={A_1,A_2\cdots,A_7}$ ,其中，7位话务员的技能分别为：

$$A_1= \{a,b,c,d\},A_2= \{e,f,g,h\},A_3 = \{i,j,k,l\}\\ A_4 = \{a,e\},A_5 = \{i,b,f,g\},A_6 = \{c,e,h,j,k,l\},A_7 = \{l\}$$

对于最小全覆盖问题：

话务员集合 $C_1 = {A_1,A_2,A_3,A_4}$和$C_2={A_1,A_5,A_6}$ 中的话务员都能满足客户所有类型的需求。但是集族$C_1$需要4位话务员，而集族$C_2$ 只需要3为话务员。因此$C_1$并不可能是$U$的最小全覆盖，而不存在两位话务员的集合就能实现全覆盖，因此$C_2$ 是全集U的一个最小全覆盖。

当然，$S={A_1,A_2,A_3}$ 也是一个大小为3 的全覆盖

对于最大覆盖问题：

假定只能制定两名话务员向客户提供服务，应该选择那两位话务员呢？

由于第6位话务员包含了6种技能，是所有话务员中技能最多的，为了使得应对的客户需求尽可能的多，可以把第6位作为候选之一。而且${A_1,A_2,A_3,A_5}$都有4种业务技能，且：

$$A_1\cap A_6 = \{c\},A_2\cap A_6 = \{e,h\}\\ A_3\cap A_6 = \{j,k,l\},A_5\cap A_6 = \{\empty\}$$

进一步：

$$\abs{A_1\cap A_6} = 9,\abs{A_2\cap A_6} = 8\\ \abs{A_3\cap A_6} =7,\abs{A_5\cap A_6} = 10$$

因此，集族$C={A_5,A_6}$ 能够覆盖客户10类不同的需求，因此集族$C={A_5,A_6}$ 构成$k=2$时的最大覆盖

对于这种小数据量问题，从中发现最大覆盖还是比较容易的。但是很多应用中数据规模都很大，比如在文本摘要中全集可以是一些关键词。给定的语料中可能包含成千上万的句子，此时要发现最大覆盖就不那么容易了

抽取式文本摘要

给定用户定义的n个关键词组成的集合 $W={w_1,w_2\cdots,w_n}$ 和 m个候选句子集合$\mathcal S = {s_i|s_i\sub W,i=1,2\cdots,m}$ ，其中句子$s_i$ 表示该句子包含的关键词集合。抽取式文本摘要问题旨在选择k个句子，使得这k个句子能够包含最多数量的关键词

用整数规划的形式来表达，可以是：

令$\mathscr{C}$ 为找出的k个句子，那么设

$$x_i=\cases{1,S_i\in \mathscr C\\0,S_i\notin\mathscr C} \\~\\ y_i = \cases{1,w_j\in \bigcup_{S\in \mathscr T}S\\0,w_j\notin \bigcup_{S\in\mathscr T}S}$$

整数规划问题可写为：

$$\begin{align} &\max \sum_j y_j\\ s.t.&\sum_i x_i\leq k\\ &\sum_{w_j\in S_i} x_i\geq y_j\\ &x_i\in\{0,1\},\forall i\in[m]\\ &y_j\in\{0,1\},\forall j\in [n] \end{align}$$

爬山算法

爬山算法是一个解决子模优化问题的局部搜索算法。下图是爬山算法的一个实例，它解决了最大子覆盖问题。该算法在每次迭代过程中选择使得集合覆盖函数$f(A)$边际增幅最大 的候选元素u，通过不停地迭代，从一个候选结果想另一个候选结果”移动”直到终止条件满足

例子

假设给定的关键词集合为 $W={w_1,w_2\cdots,w_S}$ ，共有9个候选句子$D={s_1,s_2\cdots,s_9}$ ，用于文本摘要，其中这9个句子包含的关键词分别为：

$$\begin{align} &s_1 = \{w_1,w_2,w_8\}~s_2=\{w_1,w_3,w_7\}~s_3 = \{w_1,w_6\}\\ &s_4 = \{w_1,w_3,w_7,w_8\}~s_5=\{w_1,w_5,w_6\}~s_6 = \{w_1,w_5,w_8\}\\ &s_7 = \{w_5\},s_8 = \{w_1,w_4,w_6\} ,s_9 = \{w_2,w_8\} \end{align}$$

• 第一轮迭代：

子集	f(A)	$f(A\cup A_i)$	$\Delta$
$s_1$	0	3	3
$s_2$	0	3	3
$s_3$	0	2	2
$s_4$	0	4	4
$s_5$	0	3	3
$s_6$	0	3	3
$s_7$	0	1	1
$s_8$	0	3	3
$s_9$	0	2	2

我们看到，第一轮，一定是选择包含关键词最多的那个句子，也就是 $s_4$. 现在，$f(A) = {w_1,w_3,w_7,w_8}$

• 第二轮迭代：

子集	f(A)	$f(A\cup A_i)$	$\Delta$
$s_1$	4	5	1
$s_2$	4	4	0
$s_3$	4	5	1
$s_5$	4	6	2
$s_6$	4	5	1
$s_7$	4	5	1
$s_8$	4	6	2
$s_9$	4	5	1

在第二轮迭代中，边际效益就少了很多了，我们看到 边际效益最大的是 $s_5,s_8$，这里选择靠前的，也就是$s_5$, 更新 $f(A) = {w_1,w_3,w_5,w_6,w_7,w_8}$

• 第三轮迭代

子集	f(A)	$f(A\cup A_i)$	$\Delta$
$s_1$	6	7	1
$s_2$	6	6	0
$s_3$	6	6	0
$s_6$	6	6	0
$s_7$	6	6	0
$s_8$	6	7	1
$s_9$	6	7	1

第三轮迭代，大多数边际效益都为0了，这里选择 最靠前的边际效益最大的句子 $s_1$

因此，我们看见，爬山算法并不是只有一种结果，只要让$f(A)$ 到达终止条件即可