注意力机制
RNNs+attention
在写 循环神经网络 这篇博客的时候,我曾简单讲过注意力机制的原理及其作用。现在我们来详细学习一下注意力机制。
首先,我们要知道注意力机制在RNN中的作用有哪些?
- 计算机视觉中的应用: 图片描述
- 自然语言处理中的应用:机器翻译
不使用注意力机制-图像识别
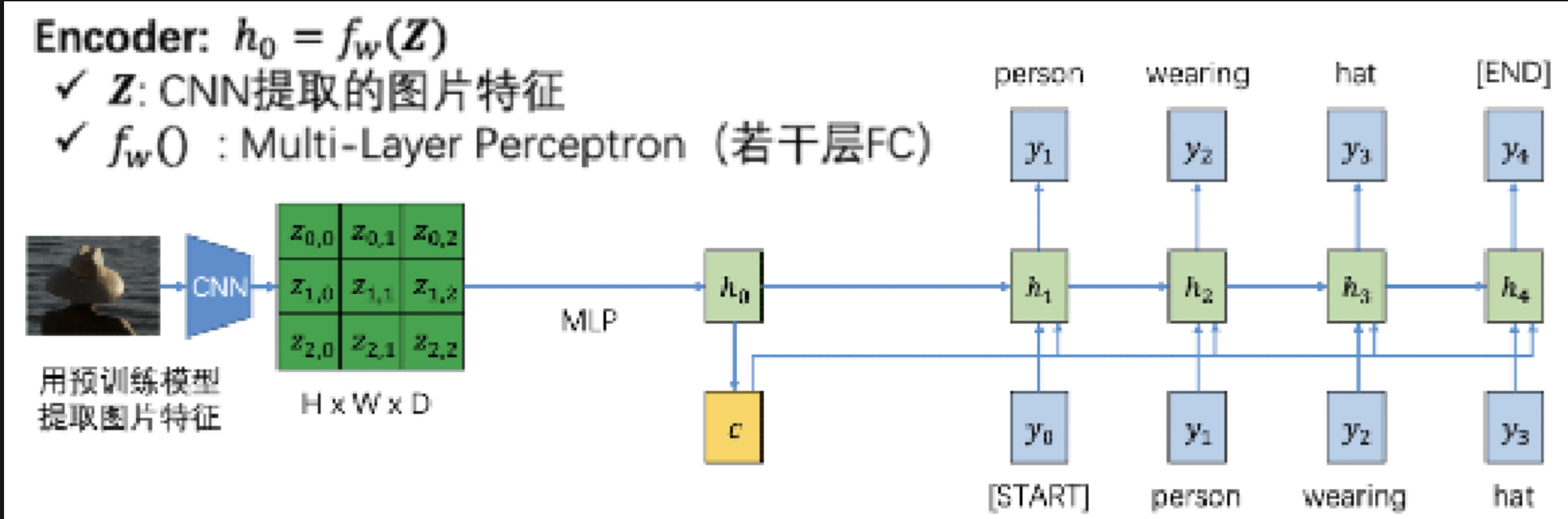
我们来讲不使用注意力机制的RNN是如何进行看图说话的。我们看到上图的左半侧是一个encoder,输入的是图片$I$, 右半侧是decoder,输出的是文本
首先,图像经过CNN卷积以后生成一张 feature map,也就是上面绿色的矩阵
然后,我们将feature map 经过 MLP (multi-layer perceptron,多层感知机)后,变成一个D维的$h_0$。 同时,利用 $h_0$ 转化出一个 context vector c(为了方便其实一般就是将$c$设置为整个$h_0$),使其保留了图片中的特征信息,可以用来辅助文本预测。
context vector 是可以作为选择性输入的,有没有都可以。如果将其作为一部分输入,那么神经元既有之前生成的文本信息,又有保留下来的图片信息,可以帮助RNN更好辅助生成单词。
但是这样做是有一个缺陷的,就是我们生成的context vector虽然拥有图片的全部特征,但对于每一个神经元的输入,都是相等的。因此,这并不利于在不同时刻捕捉差异化的图片信息,神经网络说话的时候就”抓不住重点“,导致看图说话效果不好。
使用注意力机制-图像识别
因此,看图说话借鉴了机器翻译中的注意力机制来提升看图说话的准确性
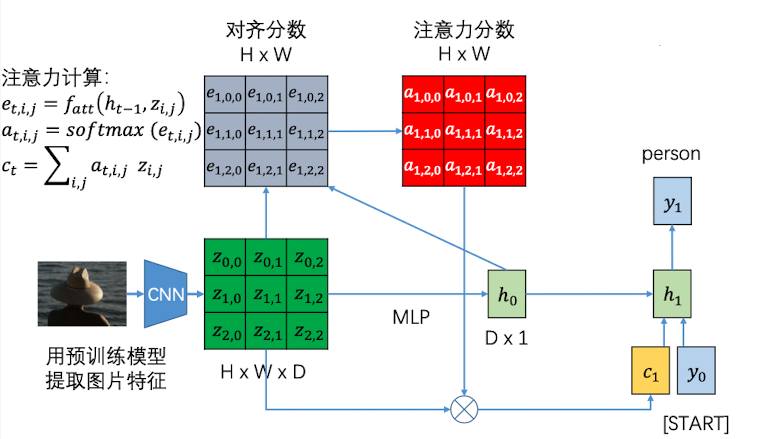
首先,还是图片通过CNN 生成一张feature map,然后通过MLP生成隐层向量$h_0$
用隐向量和feature map 相乘,生成一张 $H\times W$ 的对齐分数矩阵 $\boldsymbol e$。对齐分数越大,代表应该关注这部分特征越多。
对于对齐分数中的元素,利用 softmax 进行归一化,得到注意力分数矩阵 $\boldsymbol a$ , 这就代表了每一个部分应该被关注的概率
利用注意力分数矩阵和feature map 做对位相乘(加权聚合),得到加权之后的整张图片的特征向量context vector, 形状为 $D\times 1$
将 context vector 、输入值、以及上个隐层状态,共同作为下一个神经元的输入。接下来,每一步的$h_{i}$都会和feature map生成一个 context vector,告诉下一个神经元应该关注哪里。
通过这种方法,每个时刻 t 的 context vector 都是不一样的,是随着$h_{t-1}$ 变化而来的。因此,每个时刻都可以根据前一时刻的隐层状态去关注图片的不同区域
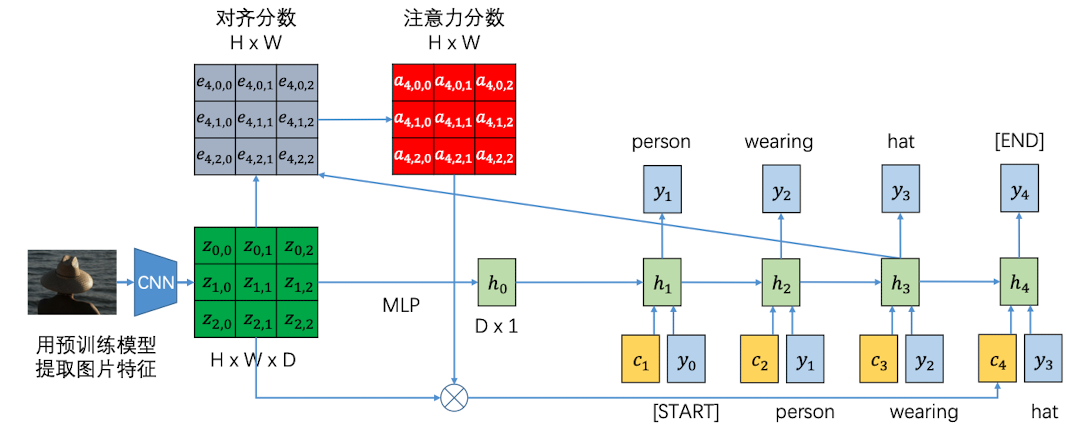
结果如下:

图像描述注意力计算
现在我们来具体看一下注意力分数是如何被计算出来的,如下图:
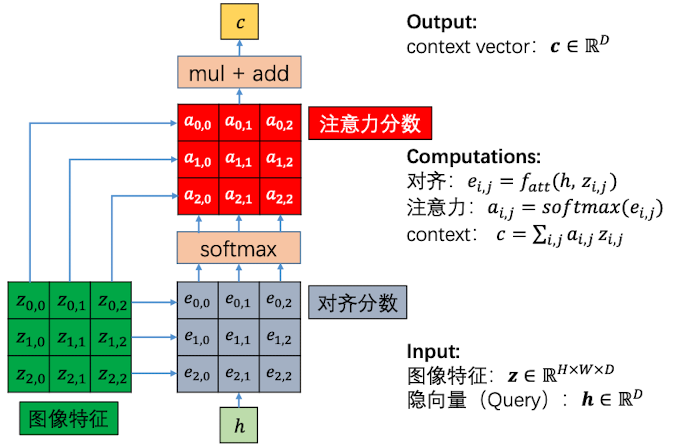
不使用注意力机制-机器翻译
机器翻译和图片识别的原理大致相同,只不过原本的encoder 是用来处理图片信息的,而现在是用来处理文字流的。因此我们不能使用CNN,而要使用RNN:
在Encoder中,一个一个输入法语单词,生成一个隐向量,聚合后经过MLP得到decoder的初始隐向量$h_0$
还可以保留一个 context vector 包含了这句法语中的所有特征,作为辅助输入来帮助文本预测,
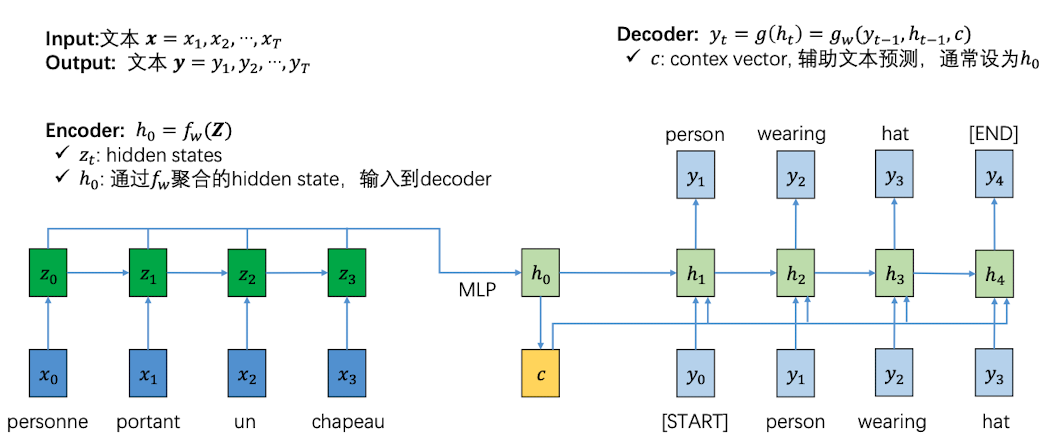
但是因为没有引入attention机制,导致decoder没有关注重点,翻译不准确
使用注意力机制-机器翻译
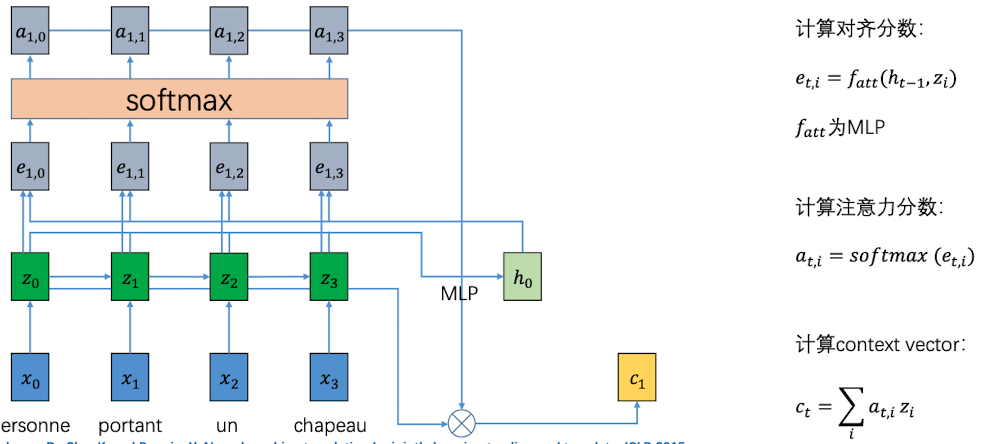
在机器翻译中引入注意力机制后,对于每一个输入层的隐向量$zi$ ,都和$h{t-1}$相乘得到对齐分数$\boldsymbol e$ ;
- 再经过 softmax 计算注意力分数$a_{t,i}$,t代表第t个时刻
- 用得到的$\boldsymbol a$和当前$z_i$ 聚合,得到context vector c, 作为下一层的输入。
这样,在decoder中,每个时刻t 的context vector 都会随着$h_{t-1}$的变化而变化,即每个时刻都可以根据前一时刻的隐层状态关注输入文本的不同部分
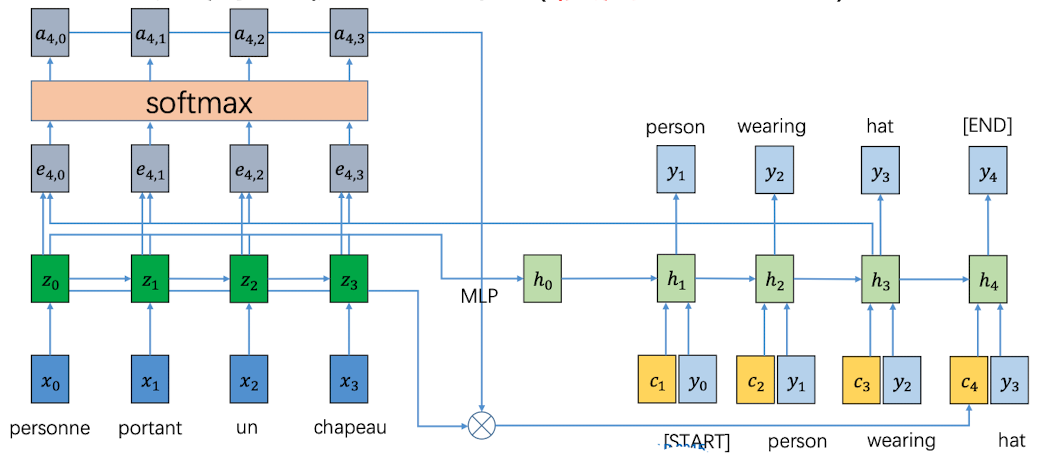
一般的注意力层结构
一般注意力层
之前我们介绍了如何在图像识别中进行注意力计算,现在我们来看看一般注意力层是如何计算的:
首先,因为一般注意力层的输入并不是feature map,而是单个的向量,因此原来的MLP变成了现在的点积,事实证明用点积计算可以在 Transformer 中取得很好的效果
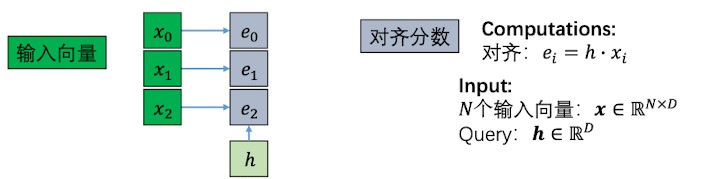
然而得到了对齐分数$e_i$,但是在向量长度很长的情况下,会造成对齐分数的方差很大(大的分数很大,小的分数很小)。这样的数据经过softmax层以后(指数运算),会使得注意力分数只集中在少数几个输入向量上。因此,单单点积还是不够的,我们需要除以$\sqrt D$ 以减轻这种效应,其中$D$为向量长度。
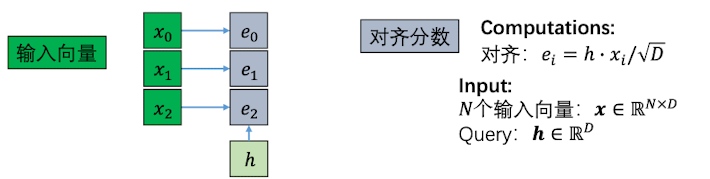
接着,对 对齐分数进行softmax以后,得到了注意力分数。在将注意力分数和输入值$x$做整合:
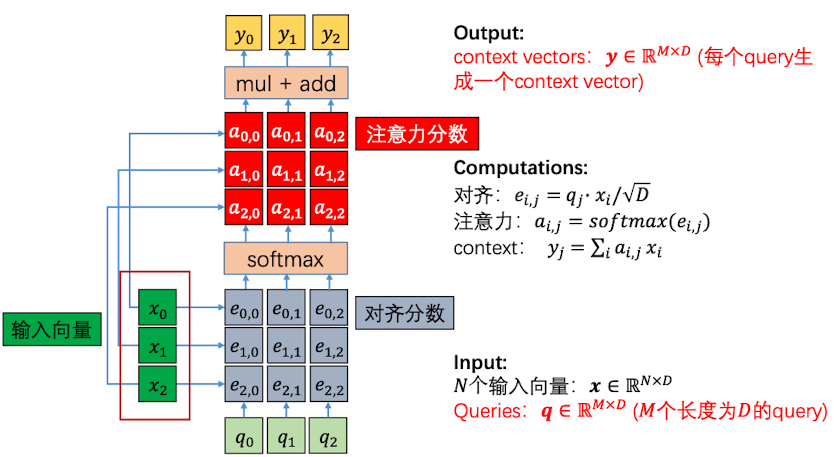
但是,这种一般注意力层是存在缺点的:输入向量既 作为对齐运算的输入,又 做为注意力运算的输入,有点缺乏输入特征上的变化。
自注意力层
因此,我们可以通过在计算对齐分数和注意力分数的时候,分别用一个线性层对输入向量进行转化来解决这个问题。这样存在一定的变化之后,可以使得 $y_i$ 的大小和输入$x_i$的大小是不一样的。
如下所示:
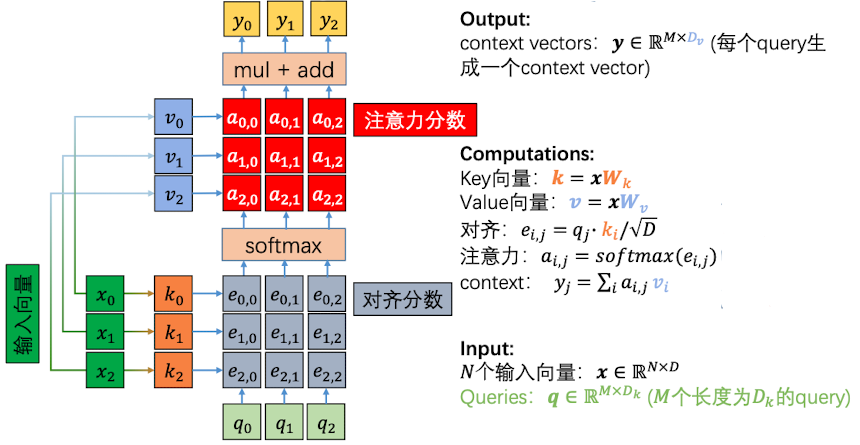
对于输入向量,我们可以将其乘以一个 $\boldsymbol W_k$矩阵将其变为 Key 向量,将其和Querie向量相乘得到对齐分数
然后再将输入值 乘以 $\boldsymbol W_v$矩阵相乘,得到 Value 向量,将其和softmax过后的对齐分数聚得到注意力分数
而且从RNN中我们也看到了,Queries 向量也是由输入向量经线性层得到的。
用自己来生成query、key去做对齐分数的计算,再与由自己来生成的value聚合,这就是自注意力层命名由来
简单来说,就是对一组输入向量的自我注意力运算,将中间的计算隐藏后,我们可以得到如下结构:
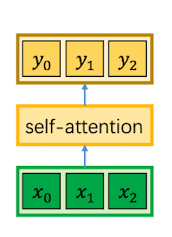
位置编码
运用自注意力层,可以完全抛弃循环神经网络中的迭代结构。因为在RNN中,context vectors是按照顺序,一个一个生成的,需要借助每一次循环的$h_{t-1}$ 。但是自注意力层只需要自己计算就可以得到 context vectors了。
因此也会导致一个问题,就是生成的编码$y_i$很可能无法学到输入向量的排列顺序信息,这对于处理文本和图片都是不利的。因此,我们要想一个办法,在输入向量中加入其在序列中的位置信息。使其能够表示每个向量的绝对位置和相对位置。
这就是位置编码 (positional encoding)的作用
关于位置编码$p_t$, 需要满足以下特性:
- 唯一性: 每个时刻的编码是唯一的
- 一致性:对于所有输入长度,两个时刻之间的距离是一致的
- 泛化性:对于所有输入长度都可以使用这套编码
因此,用三角函数来表示时刻、位置信息就是一个很好地选择。
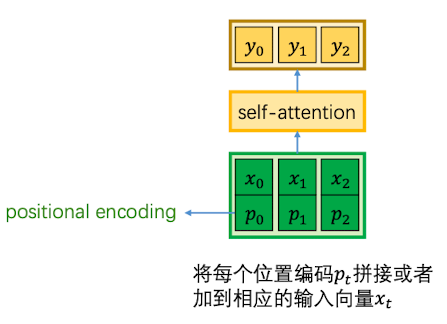
其中, $t\geq 0$ 代表时刻;$0\leq i<D$ 代表编码的第i个位置; $\omega_k = \frac{1}{10000^{2K/D}}$
最终,对于在t时刻、长度为D的输入,会得到一个长度为D的位置编码:
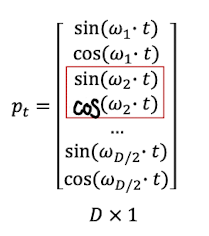
因为我们对$\omega_k$ 取得值是很小的,t乘以10000之后,可能会开始循环,但 t 一般只取128、256、512、1024。因此 $p_t$ 所有sin、cos的值都是在一个周期之内的,满足唯一性。
泛化性也很好理解,因为这套编码对任何长度的句子, 都是适用的
对于一致性,两个时刻之间的距离是一致的吗?我们可以用一个简单的方式来证明:我们考虑位置编码中任意一对sin和cos,运算以下公式:
我们发现,其距离只和两个时刻有关,和输入长度无关。因此一致性也会满足
遮挡的自注意力层
有了位置编码这个工具以后,输入向量就是由顺序性的。但现在又有一个问题,之前的注意力机制,输出结果的时候,后面的输入是看不到的。但现在有了位置编码之后,在输出$y_0$的时候却能看到后面的输入。
这是不可以的,每一个位置的输入编码是不应该提前看到后面的输入的,否则会导致过拟合的情况
因此,提出了遮挡的自注意力层。也就是说,在encode的时候,将当前向量后面的对齐分数设置为负无穷,在decode 的时候相应的注意力分数设置为0,如下图所示:
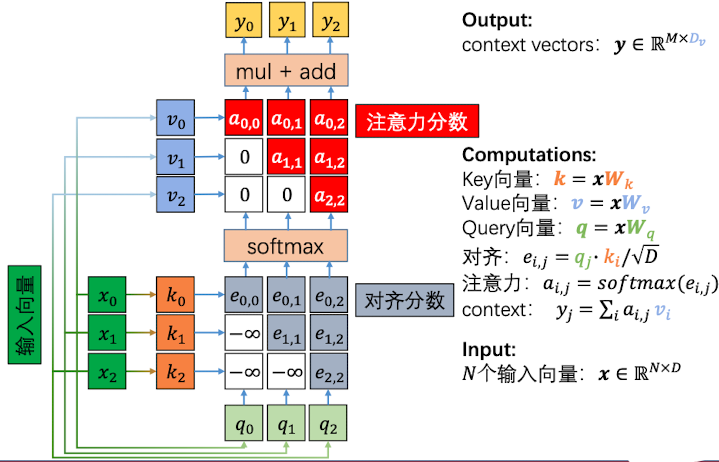
我们看到,对于第一个输入位置的$k_0$,我们把$k_1,k_2$的对齐分数置为$-\infty$;对于第二个位置输入的$k_1$,它可以看见$k_0$输入,但是$k_2$ 的对齐分数被设置为$-\infty$
多头自注意力层
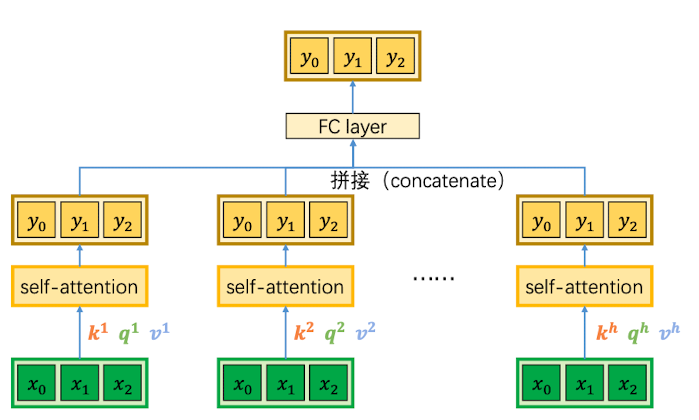
用多组不同的 $k/q/v$ 来计算多组不同的注意力分数,每组注意力分数关注输入中的不同部分,以提高对子空间的特征捕捉能力。
比如说我可以设置$h=8$,即8个head,每个 head 生成一组输出,最后将8组输出拼接
Transformers
完全基于注意力机制的全新的神经网络结构