生成模型

到现在为止，我们学习的所有模型都是有监督学习。

• 给定数据x和标签y，学习$x\rightarrow y$ 的映射，并以此预测新的数据的标签
• 应用场景如：图像分类，图像描述，目标检测，语义/实例分割，图像复原，风格转换等等。

那么，什么是无监督学习及其应用呢？

• 对于海量数据来讲，是没有标签的(或者标签就是数据本身)，给数据打标签是一件费时费力的工作。
• 应用场景如：机器学习中的聚类，降维，EM算法，表征学习，生成模型等等

这节课，我们主要来学习生成模型。简单来说，就是一个可以生成图像的模型——给定训练图像，生成行的随机图像，如下图所示：

左边是输入的数据，是真实世界里的照片；右边是模型随机生成的照片

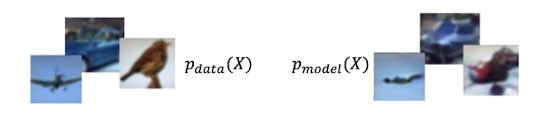
现在给出正式定义：给定观测数据 $X$ 和 目标变量$Y$,模拟联合分布$p(X,Y)$ 或 条件概率分布 $p(X|Y)$

给定观测数据和目标变量Y，模拟联合分布$p(X,Y)$ 或者条件概率分布$p(X|Y)$. 然后，由 $p(X,Y)$ 或者 $p(X|Y)$ 可以模拟概率密度函数$p(X)$

不管使用哪种方法，其底层逻辑都是极大似然函数。 在 极大似然估计与EM算法 中，我们已经学过极大似然函数是用来估计参数的。同样的在这里我们可以用到这个方法

• 构建参数模型表示图像的概率密度函数 $p{model}(x|\theta)$，(一般使用神经网络来模拟$p{model}(x|\theta)$ )
• 使用大量观测图像去估计参数$\theta$ , 使得 $\sum p_{model}(x|\theta)$ 去极大值 (优化目标)
• 使用估计(训练)好的 $p_{model}(x|\theta)$ 生成新的随机图像

$$\theta ^* = \arg\max_\theta \mathbb E_{x\sim p_{data}}\log p_{\text{model}}(x|\theta)$$

现在我们给出常用的生成模型以及他们的分类

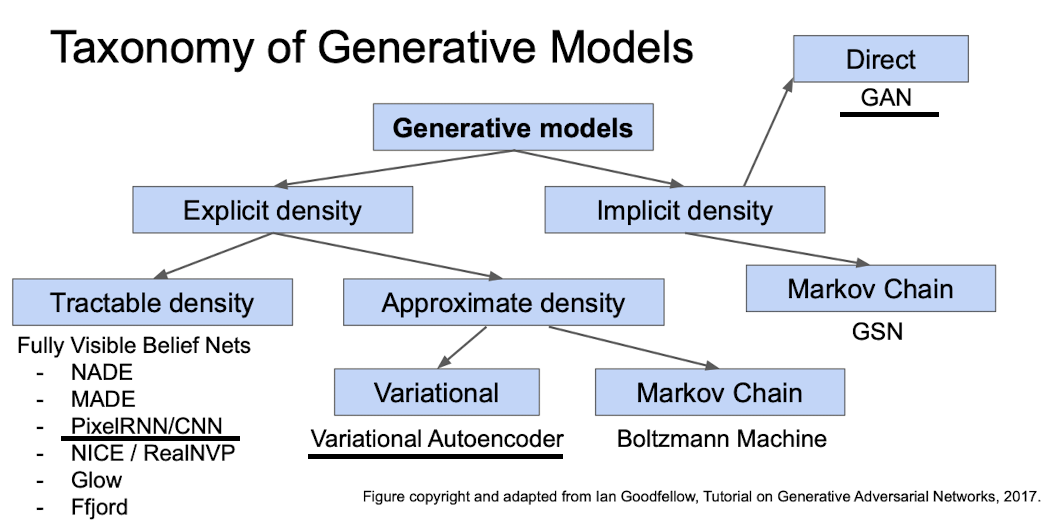
首先，生成模型分为两大类：显示的概率密度函数——即显式定义概率密度函数，然后用观测数据将其最大化；隐式的概率密度函数——预先没有定义，但是通过其他方式使得模型学习得到概率密度函数。

其中，显示概率密度函数又分为两种: 容易计算的概率密度函数和近似的概率密度函数。其中，前者最主要的技术是 完全可见信念网络 (Fully Visible Belif Nest, FVBN)，主要模型是PixelRNN/CNN； 后者主要技术为变分自编码器(Variational Auto Encoder)和马尔科夫链(玻尔兹曼机)

隐式概率密度函数中分为两种模型： GAN和GSN，GAN是我们今天要学习的模型，GSN中使用马尔科夫链，效率比较低。

显式概率密度函数

FVBN

首先我们来介绍显示概率密度函数类别下的完全可见信念网络的原理。然后来介绍一下这个网络下的PixelRNN模型

首先，我们令图片 $x ={x_1,x_2,\cdots,x_n}$为一组向量，$p(x)$ 是关于图片中所有像素值的联合概率分布。

其次，我们要计算$p(x)$ ，$p(x)$等于基于链式规则的条件概率乘积，即：

$$p(x) = \prod_{i=1}^nP(x_i|x_1,\cdots,x_{i-1})$$

• $p(x) $是代表图片x 的概率，我们可以使用神经网络来模拟高维数据的概率分布
• $p(x1,\cdots,x{i-1})$ 代表给定前面所有像素的情况想，第i个像素的值$x_i$的概率

最后，将联合概率学习转换为顺序预测：

• 根据已生成的像素预测下一个像素值
• 优化目标：最大化$L = \sum_x\log p(x)$

Pixel RNN/CNN

Pixcel RNN

从上面对 FVBN 的介绍，我们发现对像素的预测是呈序列状的，因此很适合用循环网络来解决这个问题。因此我们要定义一个比较规则的序列

最朴素的想法是：从左上角开始每次生成一个像素点，当前点为 output, 左边一个点为 input。如下图所示：

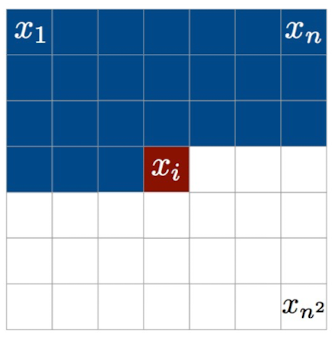
但这样训练和生成的效率都很低，我们想象一下生成512x512的图像，会导致像素序列非常长，而这么长的序列对RNN来说是非常不利的。

所以，在这篇文章中，作者提出了用Row LSTM方法和Diagonal BiLSTM方法来解决Pixel RNN的问题。

Row LSTM

Row LSTM的想法是：从上往下逐行生成像素点，即把前一行的像素全部作为 input ，如下图所示

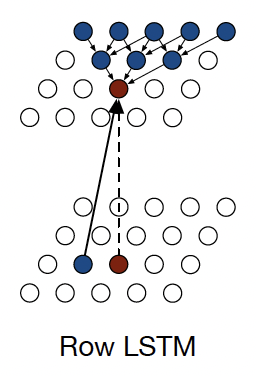
这种方法采用LSTM顺序去输出每一个像素点

$$[o_i, f_i, i_i, g_i] = (K^{ss} * h_{i-1} +K^{is} * x_i)$$

其中，$K^{is}*x_i$ 代表 $3\times 1$的卷积运算，训练时还可以让所有row 并行运算

不足之处：

• 每个像素点的 context 知识上面几行组成的三角区域，这和理想状态不符合、
• 生成时依然是每次只生成一个像素点，会存在一定的效率上的问题

Diagonal BiLSTM

要了解对角双向LSTM方法，我们首先要对双向LSTM有一个了解。其结构如下图所示：

• 两层LSTM结构，分别从正反两个方向顺序输入序列数据
• 同一个时间步的两个hidden state 拼接然后转化为输出

通过这个方法，就可以同时捕获当前时间步前面和后面的context，而不像前面Row LSTM方法那样只能捕捉前面的context

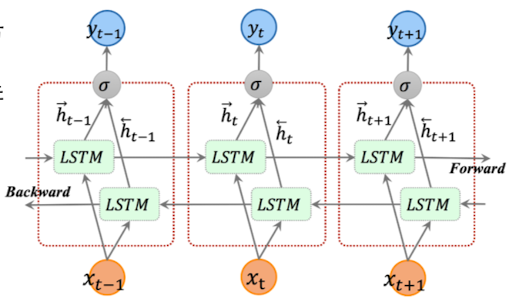
将BiLSTM应用于生成模型中去，我们看到，这里有两层LSTM：第一层从左上到右下；第二层从右上到左下。像素生成的示意图如下所示：

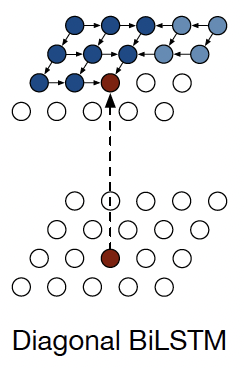
运用这种方法

• 输入为左边(右边)的像素点
• hidden state为左边(右边)和上方像素点的hidden values，并对其做$2\times1$ 卷积

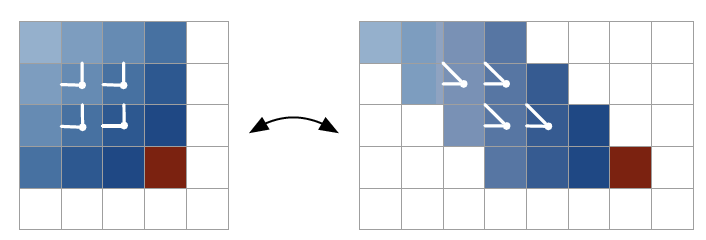
正常来说，输入值是左方和上方的像素点做卷积，但是这样不太方便矩阵计算。因此，我们每一行平移一个pixel的位置，使得左方像素和上方像素对齐，方便卷积计算。

不足之处

• 生成时依然每次生成一个像素点

  

我们看到Pixel RNN 生成的图片都非常小，因为尺寸一旦大了会导致梯度爆炸、梯度消失等问题。

Pixel CNN

使用CNN，可以用左边和上面的像素卷积后生成新像素点。在训练时可以高度并行来提高训练效率

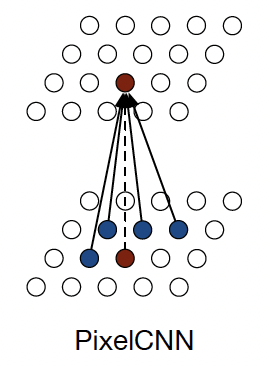
使用门结构层来代替 ReLU 层

• $t = \tanh (\boldsymbol W{k,f}*x)\odot\sigma(\boldsymbol W{k,g}*x)$
• 加强网络的 non-linearity

不足之处：

生成的时候仍然每次生成一个像素点。

总结

Pixel RNN和Pixel CNN的优点：

• 显示计算图像生成概率，生成图像直接和原式图像比较，易于优化，训练稳定

缺点：

• 虽然训练时候可以利用并行增加效率，但是测试的时候只能一个一个生成咸水沽。

改进：

• Sigmoid 代替 Softmax
• 将 RGB像素视为整体
• Res connections
• Dropout

总的来说， FVBN就是定义了一个离散的、易处理的(tractable) 密度函数，利用训练集直接优化似然(直接寻找极大似然).

$$p(x) = \prod_{i=1}^n p(x_i|x_1,\cdots,x_{i-1})$$

VAE

VAE的全称是(Variational Autoencoders) ，相比于FVBN，它定义了一个连续的、不易处理的密度函数，是通过优化似然的下界(lower bound)来逼近极大似然的方法.因此，这里要是用积分来定义公式

$$p(x) = \int p(z)p(x|z)dz$$

自编码器

那么要了解VAE，首先要对自编码器(Autoencoders ,AE) 有一定的了解。自编码器是一种通过无监督的方式去学习数据内在表征(降维)的神经网络，如下图所示：

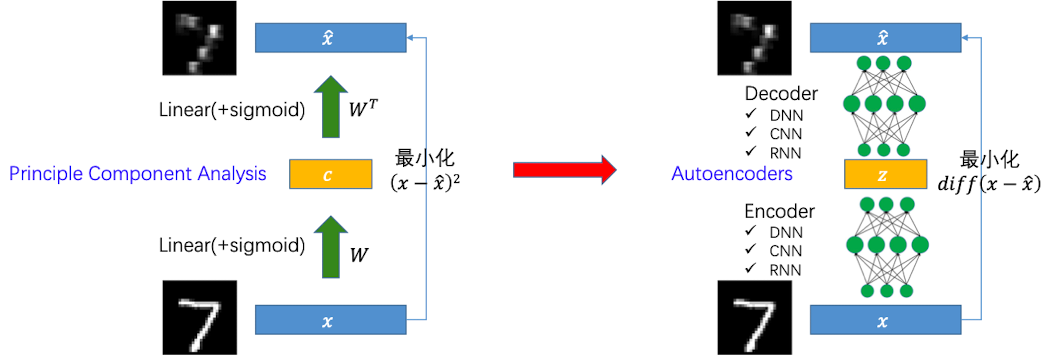
左侧是PCA的方法进行一个降维，右侧是通过自编码器方法对图片进行一个降维。它们的区别是：

• PCA是将矩阵经过sigmoid激活后保留主成分达到降维的目的，然后通过和$W^T$ 相乘获得新的压缩后的图片
• 自编码器则是通过一系列神经网络(编码器)将图片变成一个向量，然后再通过一些列神经网络(解码器)将这个向量复原成一张图片

他们的效果对比如下，我们看到自编码器相对于PCA有更多的参数，但复原后的图片也更加清晰

使用自编码器进行预训练

自编码器有什么应用场景呢？

首先，训练一个能够用于重构输入的隐层向量表示：

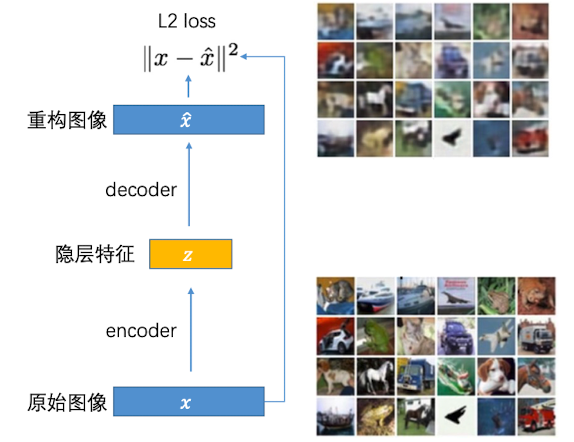
然后，训练完毕后，隐层特征就可以用于其他有监督训练任务(例如有大量数据，却只有少量标签)

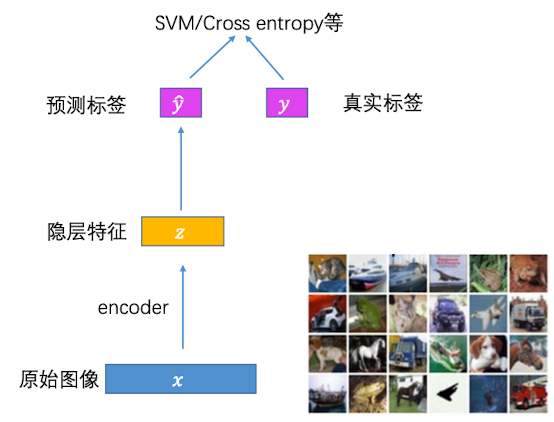
那么我们可不可以随机初始化一个隐层向量，然后通过decoder来生成图像呢？这是比较困难的。因为用固定的自编码器去生成图片的时候，虽然隐层向量空间是连续的，但是每张图片生成的向量是离散的。处于离散向量之外的其他向量，不一定能生成图片。

就如同下图，虽然自编码器可以压缩黑狗还原黑狗，压缩白狗还原白狗，但是处于黑狗和白狗之间的那部分向量，是不一定能生成斑点狗的

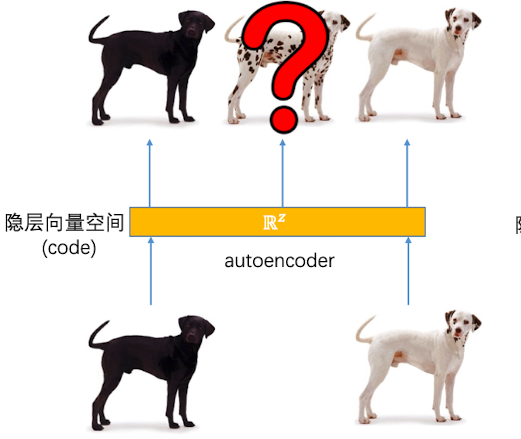
VAE的原理

由此，我们提出，在自编码器的隐层向量空间中加入一些噪音，使得自编码器也能够生成斑点狗的照片：

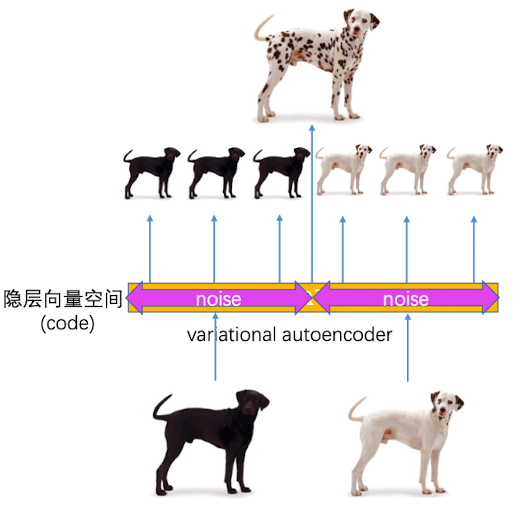
那么既然我们定义在连续空间上，因此VAE的概率密度函数也得是连续的，由此得到了公式

$$p(x) = \int p(z) p(x|z)dz$$

其中：$x$ 是图像，而$z$ 是可以是隐层向量空间里面的一个随机向量(连续变量)。所以对于每一个z可能会生成一张图片。

用VAE模型生成图像

VAE模型怎么去生成一张图像？

• 首先，从高斯分布中生成一个随机变量z，使得 $z\sim N(0,I)~$

• 让每个$z$ 去生成令一个正态分布 $N(\mu(z),\sigma(z))$

• 让 $x|z$ 服从正态分布 $N(\mu(z),\sigma(z))$
• $\mu,\sigma$ 两个函数可以用神经网络表示
• 因为z可以一直生成，因此理论上$p(x)$ 可以表示成无穷多个正态分布的mixture(即 $p(x) = \int p(z)p(x|z)dz$ ）。但事实上训练的图片是有限的，因此, 训练目标为最大化$\prod_xp(x)$或$\sum_x\log(p(x))$

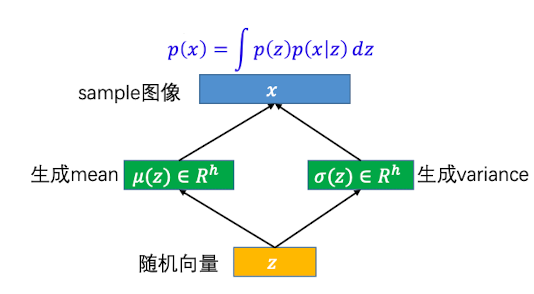
但事实上z不可能随机生成的，而是要根据我们的输入图片学习而来的(巧妇难为无米之炊)。放在数学层面上解释，就是我们要去寻找后验概率$p(z|x)$

这部分，就是自编码器中 decoder 的部分

后验概率

后验概率其实就是上述步骤反过来，扮演一个 encoder的部分

我们引入近似概率$q(z|x)$,使得：

• 每个x生成一个正态分布 $N(\mu(x),\sigma(x))$
• $z|x$ 服从正态分布$N(\mu(x),\sigma(x))$
• $\mu,\sigma$ 两个函数可以用神经网络表示，使得 $q(z|x)$尽可能逼近$p(z)$

将两部分放在一起看，如下所示

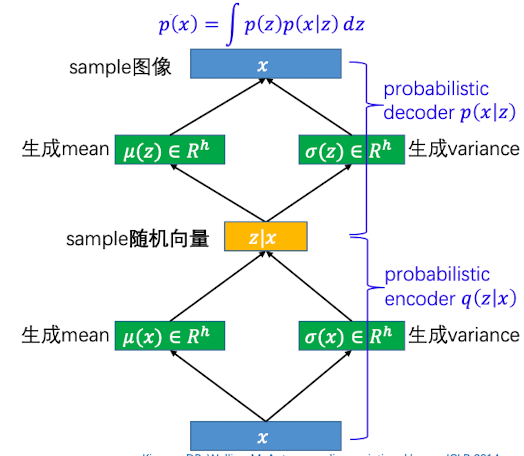
所以说，VAE和AE的原理是一样的，都是由图片生成向量，再由向量去还原图片。区别在于AE里面中间的向量是固定的，而VAE中间的向量是根据分布随机生成的。

极大似然估计

因为我们的目标是最大化$L = \sum_x\log p(x)$, 对于概率密度函数$p(x) = \int p(z)p(x|z)dz$ ，直接计算是不易处理的，因此我们需要用近似的方法将其变得更容易处理一点

$$\begin{align} \log p(x) &= \log p(x)\int q(z|x)dz\\ &= \int q(z|x)\log p(x)dz\\ &=\int q(z|x)\log (\frac{p(z,x)}{p(z|x)}) dz\\ &=\int q(z|x)\log(\frac{p(z,x)}{q(z|x)}\frac{q(z|x)}{p(z|x)}) dz\\ &=\int q(z|x)\log(\frac{p(z,x)}{q(z|x)})dz+\int q(z|x)\log (\frac{q(z|x)}{p(z|x)})dz \end{align}$$

其中，最后一式的第二部分是$KL$散度， 肯定是大于等于0的，因此

$$\log p(x) \geq \int q(z|x)\log (\frac{p(x|z)p(z)}{q(z|x)})dz$$

这个就是$\log p(x)$ 的下界，我们令其为 $L_b$。 因此，目标函数可以转化为 $L= \sum _x L_b$

下一步，我们知道了$Lb$的公式如下，我们就要去寻找$p(x|z)$和$q(z|x)$ ，求得$L_b$的极大似然估计，使得$\sum{x}L_b$最大化

$$L_b = \int q(z|x) \log(\frac{p(x|z)p(z)}{q(z|x)})dz\\$$ $$\begin{align} L_b& = \int q(z|x)\log p(x|z) dz + \int q(z|x) \log (\frac{p(z)}{q(z|x)})dz\\ &=\int q(z|x)\log(x|z)dz-\int q(z|x)\log(\frac{q(z|x)}{p(z)})dz\\ & = \text{E}_{q(z|x)}\log p(x|z)-D_{KL}(q(z|x)||p(z)) \end{align}$$

我们的目标是最大化前半部分$\text{E}_{q(z|x)}\log p(x|z)$ 重构图像概率，以及最小化后半部分后延概率分布$q(z|x)$和高斯分布$p(z)$之间的差异

VAE 的训练

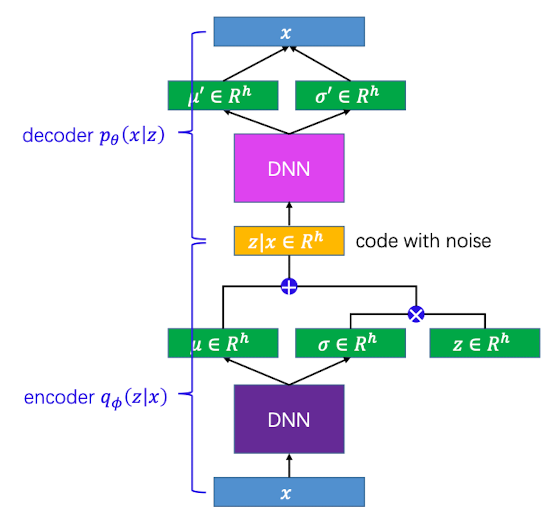
• 最小化 $D{KL}(q\phi(z|x)|| p(z))$ , 即 $\max L{q\phi} = \sum_j 1+\log(\sigma_j^2)-\mu_j^2-\sigma_j^2$
• 最大化$E{q\phi}\log p\theta(x|z)$ , 即 $\max L{p\theta} = \sum_l\log p\theta(x|z_l)$

我们的目标方程也变成了：$L = \sum_iL_i$, 其中：

• $Li = \frac{1}{2}L{q\phi}^i+\frac{1}{L}L{p_\theta}^i$

我们可以用随机梯度上升的方式来最大化$L$

VAE 图像生成

训练完毕后，我们已经得到了$q(z|x)$ ，因此可以扔掉 encoder，只保留decoder.

因为我们加了noise，所以对于连续空间里面的每一个随机向量z，都保留了一定的特征，因此都可以生成一张随机的图片。

Input 为：随机向量$z\sim N(0,I)$

Output为：一张随机图像

VAE效果如下

总结

VAE 的优点：

• 显示计算图像生成概率，生成图像直接和原始图像进行比较，易于优化，训练稳定
• 相对于Pixel RNN 训练较快

缺点：

• 计算的是极大似然的下界
• 使用MSE计算原图和生成图像的差异，不能保证复原真实图片，导致生成图像比较模糊

这是因为，VAE只是通过采样正态分布来尝试记住真实图片的样子，将特征重新组合，并不是真正意义上生成新的图片

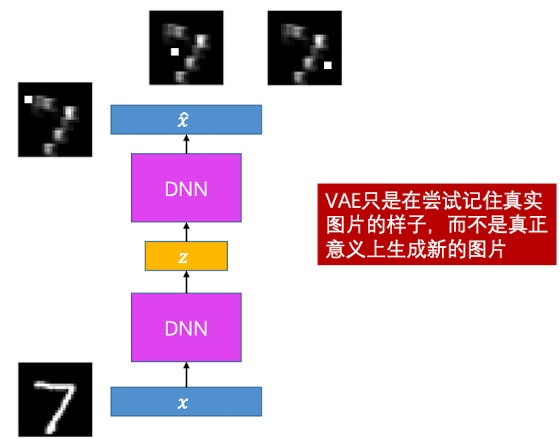
隐式的概率密度

当我们定义了显示的密度函数的话，就永远是根据已经存在的图片去生成新的图片。因此，还有一种方法是不定义显示的概率密度函数了，这样生成器就相当于从未见过真实的图片，只是根据Discriminator(鉴频器) 的反馈去不断逼近真实的图片，所以GAN也被认为是真正意义上的生成模型。

其原理如下所示：

Generator 直接从任何一个先验概率分布中生成图片，然后用一个专家 去判断这个图像是否是真的。直到专家无法分辨图像的真假的时候，就相当于生成了一张新的图片

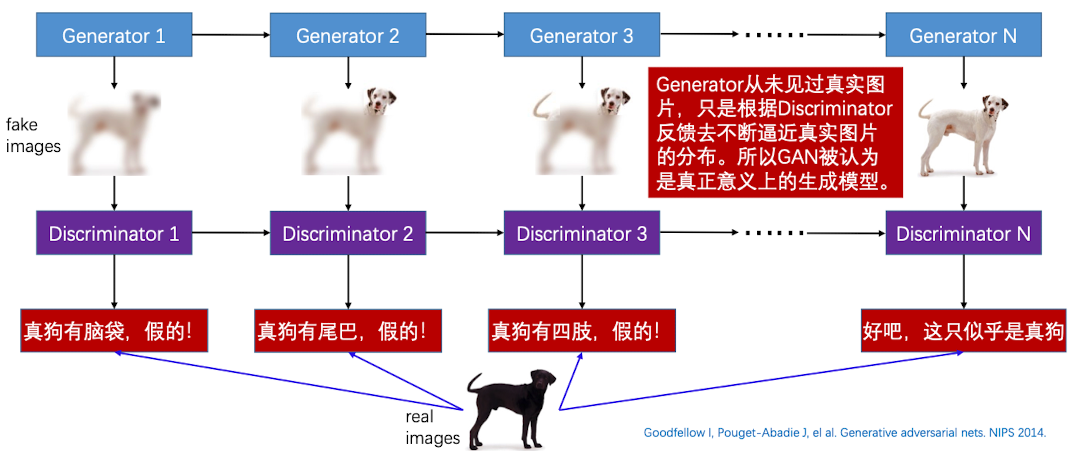
GAN

非正式解释

用非正式的语言来解释一下Gan的原理：

我们把每一张图片当一个点去看。黑色的点代表训练数据点的分布，而绿色代表GAN模型生成图片的分布。蓝色的县代表生成数据点为真的概率

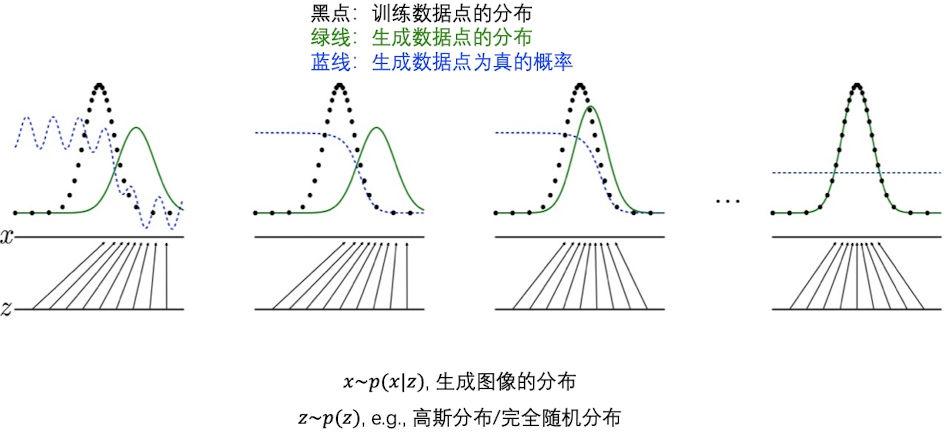
因此，我们可以看到，在一开始，数据点为真的概率是不断波动的，前半部分为1，后半部分为0(图2)。我们可以根据这个标准，让绿色的线不断逼近黑色的线，最后让它们重合。此时，蓝色的线停留在0.5处，也就是说，我不能鉴别这个绿色的点是真的还是假的图片。

模型结构

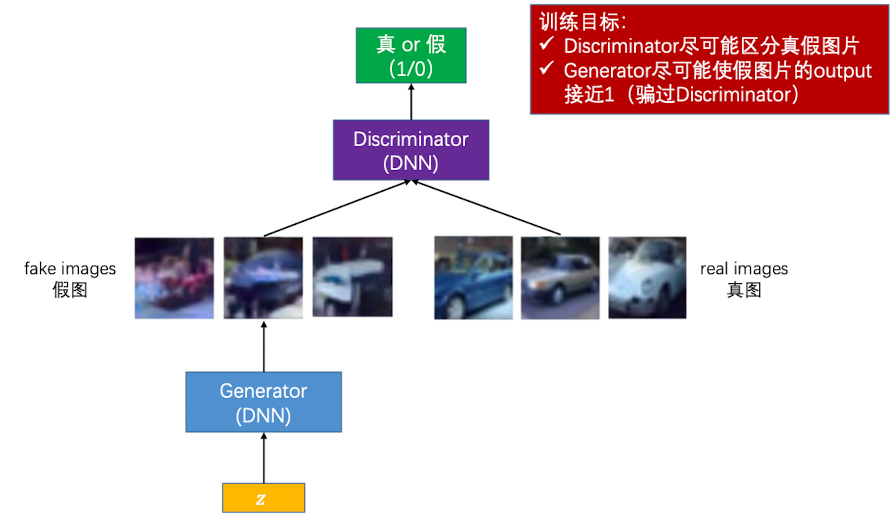
首先，给定一个假的随机向量，交给Generator生成图片，然后将生成图片和真图片共同交给 Discriminator去判断，给出真假判断。最后的训练目标就是，这个Discriminator没有办法区别生成的图片是真的还是假的。

目标函数

目标函数由两部分,如下：

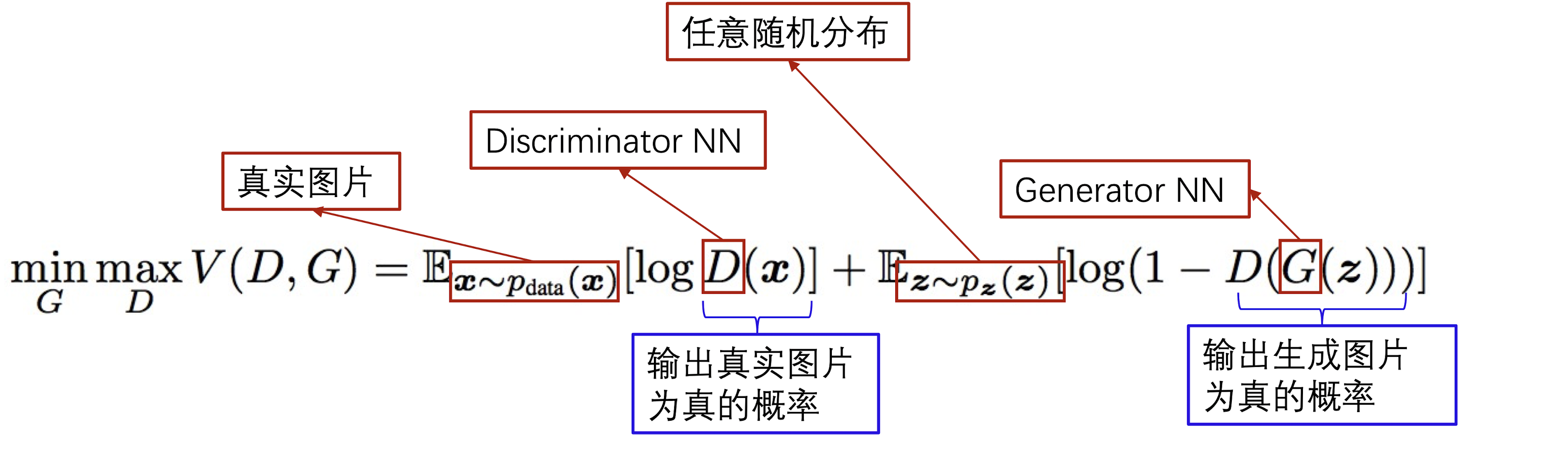
第一部分是$\max_D$,即对Discriminator的训练，让其可以尽可能区分真假图片的这个目标。因此他希望对于真的图片，对其的判断要尽量接近于1；而对于生成的图片，要尽量判断出他是假的。因此优化目标是$D(G(z))$尽量接近0

第二部分是$\min_G$ ，也就是对Generator的训练，让他生成的图片尽可能的逼近真图片，也就是让$D(G(z))$ 尽量接近1

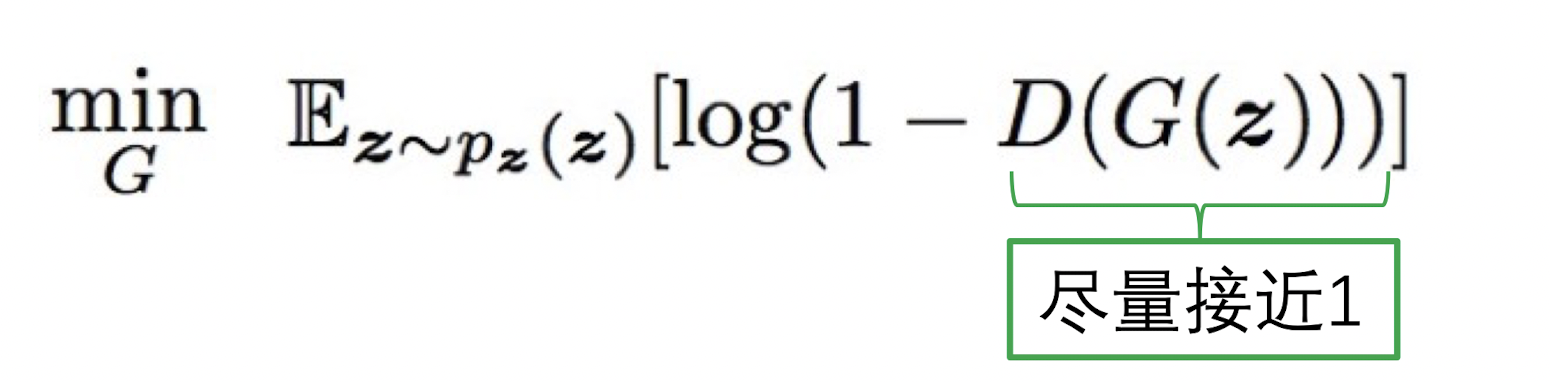
因此这就是为什么叫做生成对抗网络(GAN)了，因为两者的优化目的是相反的，一个是让 $D(G(z))$尽量接近0；另一个是让$D(G(z))$尽量接近1

GAN 训练方法

对于GAN，我们要训练n次。在每一次训练中，需要：

• 迭代k次 Discriminator：

  • 抽取 n 个随机向量${z^{(1)},\cdots,z^{(m)}}\in p(z)$ 组成 minibatch
  • 抽取 n 个图像${x^{(1)},\cdots,x^{(m)}}$ 组成minibatch
  • 使用SGA梯度上升算法更新Discriminator的参数：
  $$\nabla_{\theta_d}\frac{1}{m} \sum_{i=1}^m[\log D_{\theta_d}(x^{(i)})+\log(1- D_{\theta_d}\Big(G_{\theta_g}\Big(z^{(i)}\Big) )\Big)]$$

• 迭代一次 Generator：

  • 抽取 n 个随机向量${z^{(1)},z^{(2)},\cdots,z^{(m)} }\in p(z)$ 组成 minibatch

  • 使用SGA 更新Generator的参数：

    $$\nabla_{\theta_g} \frac{1}{m}\sum_{i=1}^m\log(D_{\theta_d}\Big(G_{\theta_g}\Big(z^{(i)}) \Big)\Big)$$

我们看到利用GAN生成的图片，每一张都是不一样的，而VAE和原图会比较相似

总结

GAN的优点：

• GAN可以完美模拟真是数据分布(只要有足够多的图片)
• Generator 根据 Discriminator 的反馈进行更新(不是尝试去记忆真实的图片)
• 生成图片的质量高

GAN的缺点

• 没有显示的概率密度函数，生成图像的可解释性比较差
• 训练具有不稳定性，即Generator 和 Discriminator 较难同步
• 需要足够的图片和足够的算力，不然可能需要算很久