计算机视觉-卷积神经网络

在卷积神经网路理论中，我们简单介绍了一下卷积神经网络的原理，现在我们来系统学习神经网络的相关知识。

正向传播

在 神经网络和反向传播 中，我们学习了全连接层，那么，全连接层有什么缺陷呢？

第一层假设是 $x\in \mathbb R^{100\times100\times 3}$ ，第二层假设有4096个神经元，那么这全连接一下，就需要第一层有$30000 \times 4096\approx 1.2\text{亿}$ 个参数，这是不能承受之重啊——因此我们需要用到新的方法。

其实我们也提出了解决的方法：

• 局部pattern：每个神经元捕获局部pattern，以减少权重参数。相当于每个神经元各司其职

  

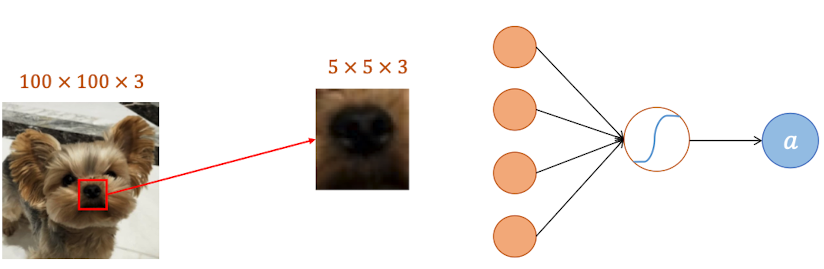
• 相似pattern：功能相似的神经元可以共享权重参数，比如两个神经元都是处理鼻子特征的，那么可以使用一套参数

  

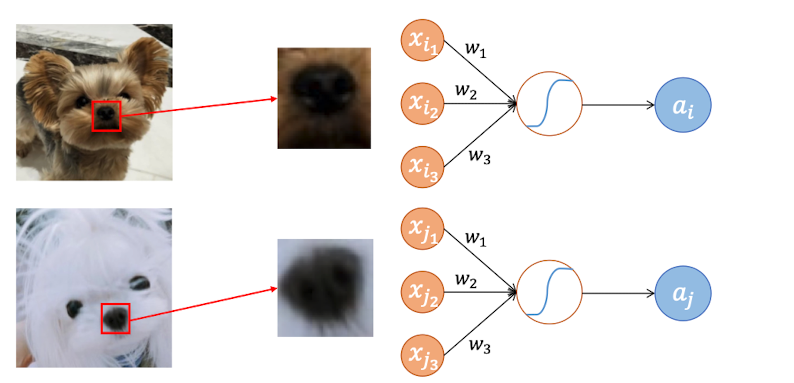
• 像素采样：可以通过压缩等方式，将像素下采样，以进一步减少参数数量

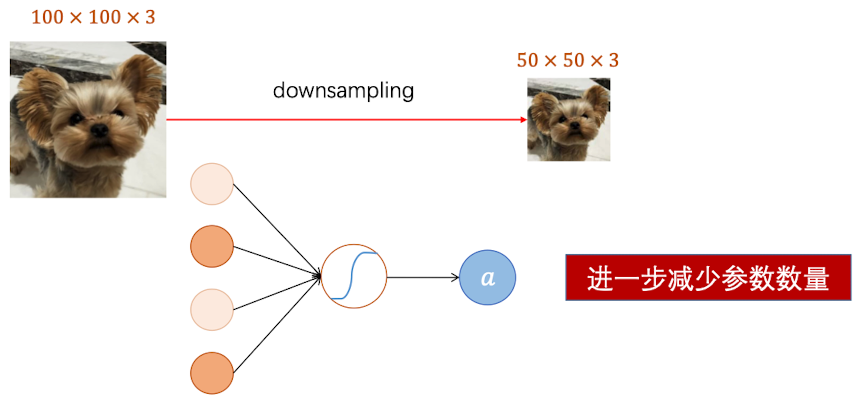
卷积神经网络

那么，把这三者结合起来，就是卷积神经网络的作用。首先，伸进网络最重要的就是理解卷积核(kernel/filter)的作用，卷积核就是一个权重矩阵(参数矩阵)，用来捕捉局部的特征，其深度和图像深度(信道数)是一样的。比如说 ,现在有一个 $32\times32\times3$ 的图像矩阵，卷积核一般很小，比如说$5\times 5$,那么其深度一定是3。

用这个卷积核和图像在$5\times 5\times3$的区域内做点积，这样就会得到一共75个值，然后将其求和，输出得到第一个神经元$a_1$ ，然后用ReLU函数激活——这整个过程就叫做一次卷积。这样一来，就避免了$32\times32\times3$的超大型权重矩阵，只需要一个小型权重矩阵即可。

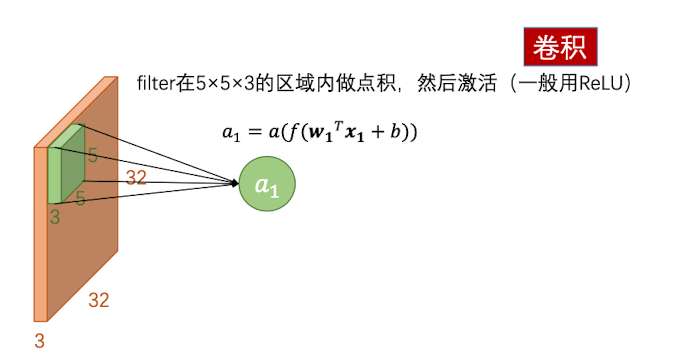
此外，由于一张图片多次出现同一个特征，因此一个卷积核对图片做一次卷积是远远不够的，需要扫描整张图片。那么该隔远扫描一次呢？这个距离就叫做步长(stride)，一般这个长度不会超过3。横向扫描一遍，接着跳到下一行再扫描一遍。整张图扫描下来，像素就会缩水一点。

比如，对$32\times32\times3$的图片用$5\times 5\times3$的卷积核卷积一遍，就会得到一张$28\times28\times1$的图片：

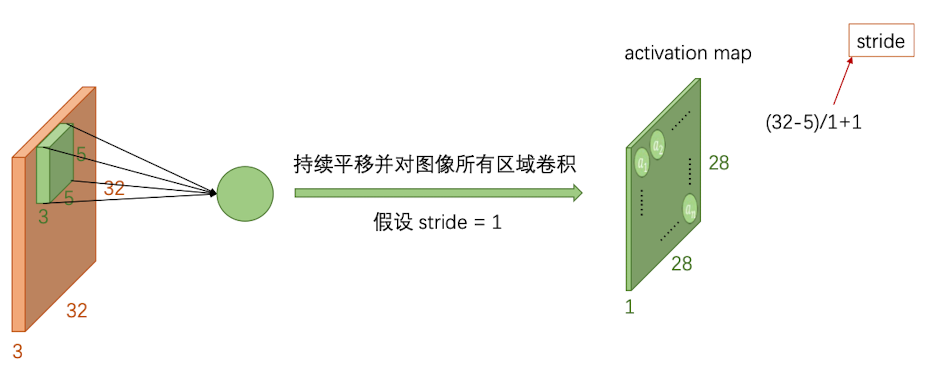
但是，一张图片不仅仅只有这一个特征，因此我们需要多个卷积核共同作用，每一个卷积核捕获不同的特征(在训练神经网络的时候会自动学习到不同特征)最后得到k层activation map

因此我们要记住：卷积核的深度和输入图片的信道数有关，而activation maps的深度适合卷积核的个数有关的

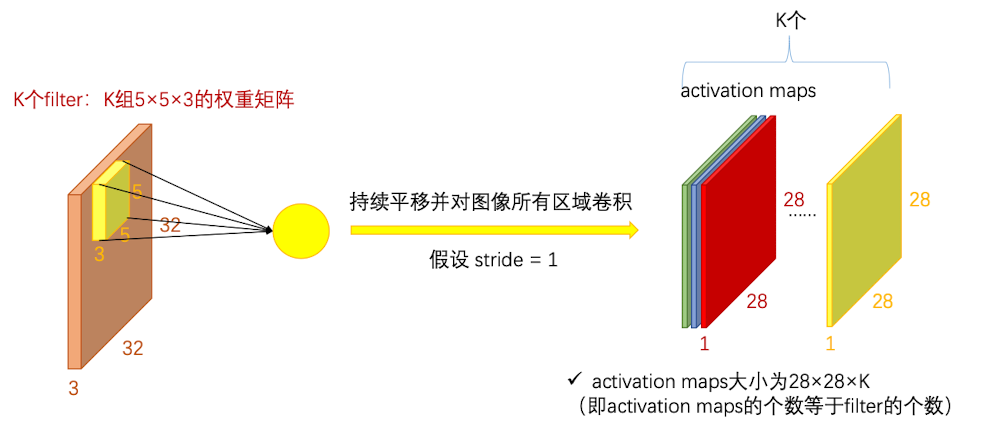
卷积层

上面得到的activation maps其实就是一个卷积层，而对于这个卷积层，又会有其他卷积核对其进行卷积，最后达成对原始图片进行不断地降维的目标。

FC层 vs 卷积层

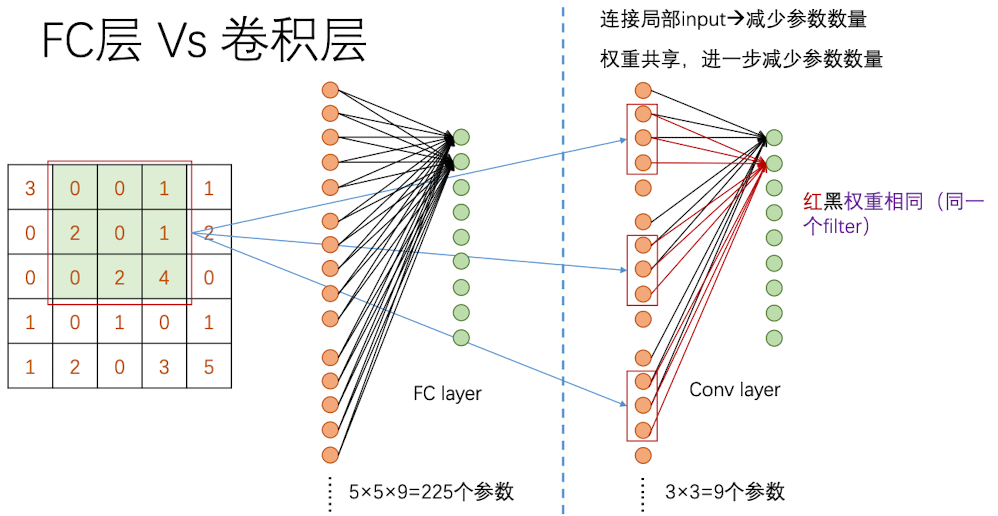
现在我们来看看全连接层(仿射层/FC层)和卷积层的对比。为了方便，我们拿$5\times5\times1$的输入图像作为例子；全连接层拿9个神经元作为例子，卷积核以$3\times3\times1$为例

如果是全连接层，要得到一个神经元的输入值，需要每个位置的像素点和权重做乘积后求和，那么这一层就一共需要$5\times5\times9=225$个参数。但是对于卷积层来说，不是一行一行去做卷积的，而是一个区域一个区域去做卷积。因此对整张图扫描一遍后会得到$3\times3\times1$的卷积层，同样是九个神经元。但是，因为使用同一个卷积核，其参数是不会变的——9个，也就是卷积核的大小。要达到和仿射层一样的参数水平，我们需要用到25个卷积核，但一般来说并不需要那么多捕捉特征的卷积核。

因此通过权重共享和局部全连接两种方式，可以明显减少参数的数量。

那么，如果当stride取2的时候，对于上述例子，一共只需要输出4个神经元就可以了，为后续减少了更多负担(当然也不可避免的失去一些信息)

Zero Padding

细心的同学们可能发现，图像边缘的像素做的卷积次数要比图像中间像素做的要少很多。因此有可能导致边缘的pattern无法被卷积核有效捕捉。为了解决这个问题，我们可以用0对图像的边缘进行补充，使得整张图片都位于图像里面：

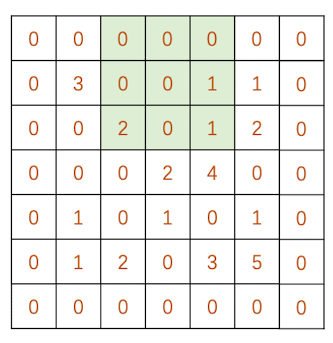
比如说，对于$N\times N$ 的图片，$F\times F$的卷积核，步长为1，padding为1，最终得到的activation map 的边长为：

$$(N+1\times2-F)/1+1$$

这是因为，padding会给图像的左右两边同时加上一列，因此我们要乘以2.

事实上，由于卷积核的大小不同，为了保持卷积后activation map的大小不变，一般我们会取不同的padding。

• 当F=3, padding 大小可取1， $2\times1-3=-1$
• 当F=5, padding 大小可取2， $2\times2-5=-1$
• 当F=7, padding 大小可取3， $2\times3-7=-1$

Activation Maps

现在我们来做一个小练习：考虑两层的卷积神经网络。输入层图像的大小为$32\times 32\times3$, 第一层一共有6个$7\times7 \times3$的卷积核，第二层是10个$5\times5\times6$的卷积核。第一层有大小为2的padding，两层的stride均为1。请给出每层的activation maps的大小、深度, 以及每一层参数的个数。

首先，我们计算第一个activation maps的边长：

$$(32+2\times2-7)/1+1=30$$

第一个activation maps的深度等于该层卷积核的个数，也就是6

因此，第一个activation map的大小为：$30\times30\times6$

参数个数为卷积核的个数 乘以 卷积核的大小加上偏置项(一般为1)，即 $6\times(7\times7\times3+1)=888$

然后计算第二层activation maps的边长：

$$(30-5)/1+1=26$$

第二层activation maps的深度等于该层卷积核的个数，也就是10

因此，第二个activation maps的大小为：$26\times26\times10$

参数个数为$10\times(5\times5\times 6+1)=1510$

小结

现在我们对卷积层做一个小结，并总结出一套通用的计算公式

• 设当前层的输入矩阵为： $W_1\times H_1\times D_1$
• 设置4个必要的超参数：
  • filter的个数$K$, 大小(边长)为 $F$, 因此可以确定有 $K$ 个偏置项
  • stride的大小为$S$
  • Zero padding的数量为 $P$

那么由上述数据，我们可以计算得到下一层的 activation maps 的大小为:

• $W_2 = \frac{W_1-F+2P}{S}+1$
• $H_2=\frac{H_1-F+2P}{S}+1$
• $D_2=K$

第 d 个activation map是第d个filter与输入层做卷积后的结果(每个卷积都加上第d个偏置量)

最后，我们给出常用的超参数设置：

• K=32,64,128,256 ……
• F=3,S=1,P=1
• F=5,S=1,P=1或2
• F=5,S=2,P=满足整除的数
• F=1,S=1,P=0 (这个就相当于全连接，但是参数都是一样的)

池化层

池化（Pooling）：也称为欠采样或下采样。主要用于特征降维，压缩数据和参数的数量，减小过拟合，同时提高模型的容错性。因为卷积过后 activation map可能还是具有较强的线性，使用池化可以有效降低这种线性

一般来说，每隔几个 Conv+ReLU 层后，会又一层 Pooling，以有效减小参数(像素采样)

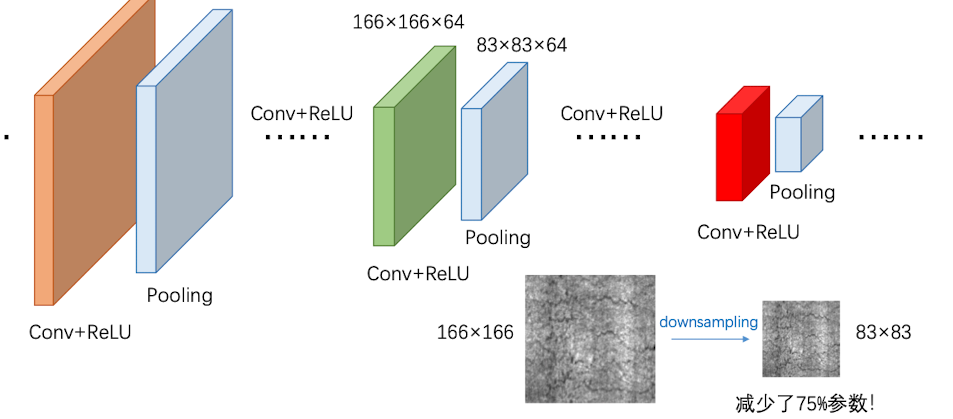
那么池化层该怎么做呢？

Pooling就相当于一个没有参数的卷积核，它对activation map中的一部分区域做mean、sum或者max操作，得到新的map。比如说，Max Pooling就是取一个部分中的最大值：(实际意义就是保留最突出的特征)

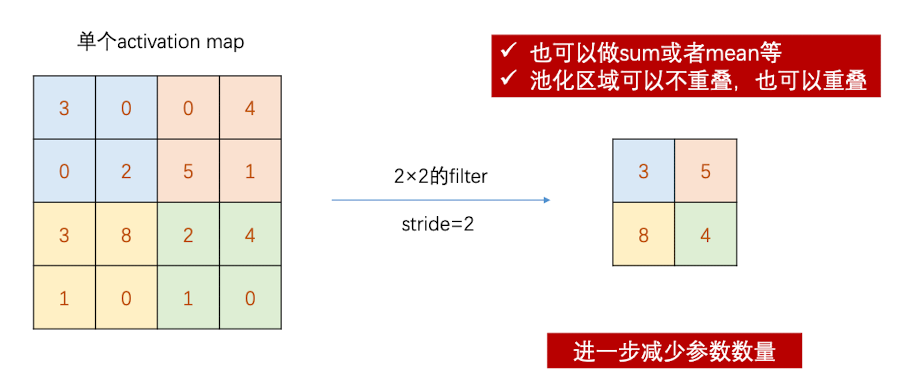
小结

假设 Conv+ReLU层的输出为 $W_1\times H_1\times D_1$

• 我们设置两个超参数

  • filter的大小(边长)为 $F$ ，只需要一个没有参数的 filter
  • Stride 大小为 $S$
  • 一般不做padding

• 一般，我们常用的设置为：

  • $F=2,S=2$
  • $F=3,S=2$

• 最后生成大小为 $W_2\times H_2\times D_2$的 feature maps

  • $W_2 = \frac{W_1-F}{S}+1$
  • $H_2=\frac{H_1-F}{S}+1$
  • $D_2=D_1$

FC层

当缩小到一定程度之后，我们对图像进行扁平化，将其压平成一列，并进行全连接，最后得到图像分类的结果

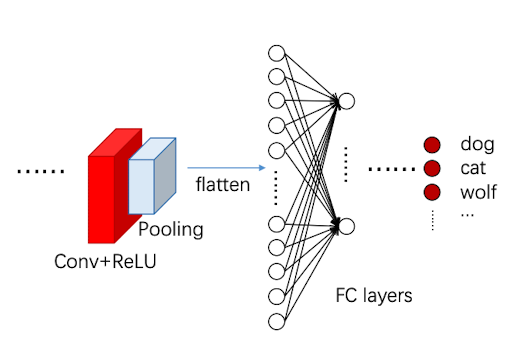
完整的CNN如下：

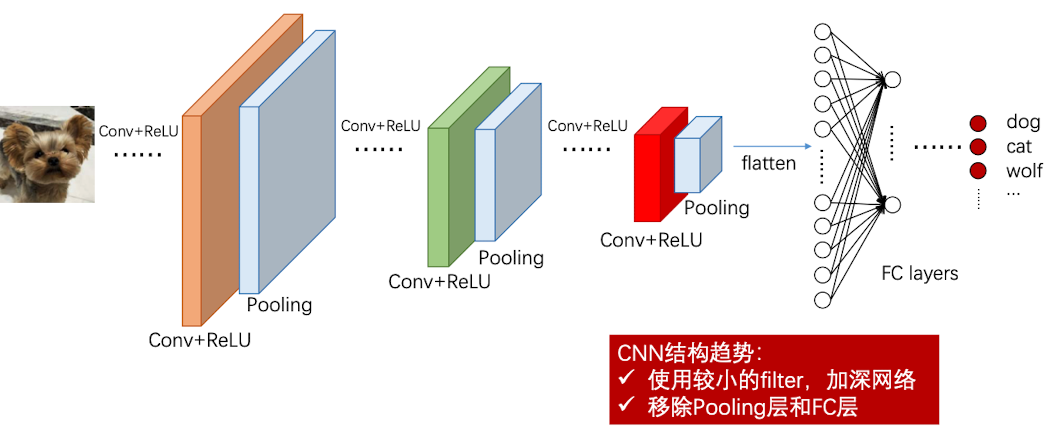
反向传播

反向传播我们倒过来看, 首先是池化层，然后是激活函数层(ReLU),最后看卷积层

Max Pooling

首先，最大池化的操作就是把一部分区域的最大值传给下一层。那么这就相当于梯度流的常见模式中的max gate。那么，在反向传播时，上游梯度就会回传到input最大的位置：

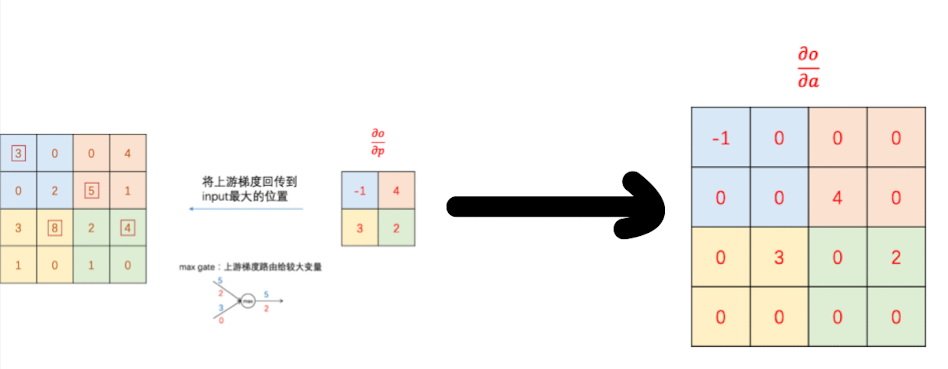
ReLU

ReLU的反向传播也很简单，如果输入层的像素大于0，那么就回传梯度，否则就回传0

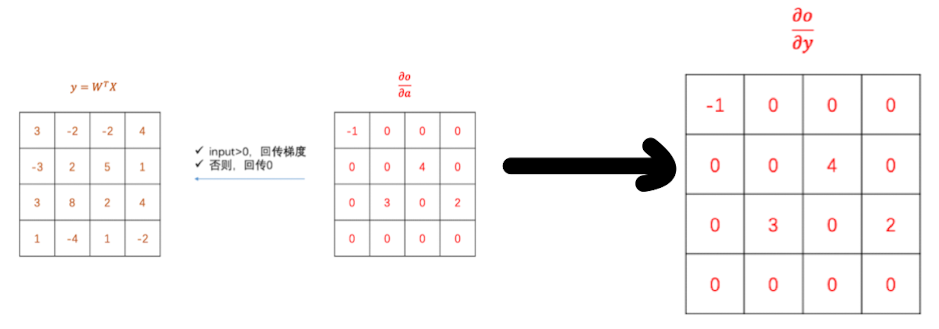
Conv

比较复杂的反向传播就是卷积层的反向传播，其实卷积层的反向传播也需要做一次卷积。

我们既要算权重的梯度，也要算输入的梯度

参考博客： https://www.cnblogs.com/pinard/p/6494810.html

我们用一个例子来推导，然后再一般化得到公式：

假设我们 $l-1$ 层的输出值 $a^{l-1}$是一个$3\times 3$的矩阵，第$l$ 层的卷积核 $W^{l}$ 是一个$2\times2$的矩阵，步长为1，那么输出的矩阵边长大小为$(3-2)/1+1=2$ 。我们不考虑偏置项，则有：

$$a^{l-1}\times W^l = z^l$$

我们列出 $a,W,z$的矩阵表达式如下：

$$\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23}\\a_{31}&a_{23}&a_{33} \end{pmatrix}*\begin{pmatrix}w_{11}&w_{12}\\w_{21}&w_{22} \end{pmatrix} = \begin{pmatrix}z_{11}&z_{12}\\z_{21}&z_{22} \end{pmatrix}$$

根据卷积的定义，我们很容易得出：

$$z_{11} = a_{11}w_{11}+a_{12}w_{12}+a_{21}w_{21}+a_{22}w_{22}\\ z_{12}= a_{12}w_{11}+a_{13}w_{12}+a_{22}w_{21}+a_{23}w_{22}\\ z_{21} = a_{21}w_{11}+a_{22}w_{12}+a_{31}w_{21}+a_{32}w_{22}\\ z_{22} = a_{22}w_{11}+a_{23}w_{12}+a_{32}w_{21}+a_{33}w_{22}$$

接着，我们模拟反向求导：

$$\nabla a^{l-1} = \frac{\partial J(\boldsymbol W,b)}{\partial a^{l-1}} = (\frac{\partial z^l}{\partial a^{l-1}})^T\frac{\partial J(\boldsymbol W,b)}{\partial z} = (\frac{\partial z^l}{\partial a^{l-1}})^T\delta^l$$

从上式可以看出，对于 $a^{l-1}$ 的梯度误差 $\nabla a^{l-1}$ ,等于第l层的梯度误差乘以 $\frac{\partial z^l}{\partial a^{l-1}}$ , 而 $\frac{\partial z^l}{\partial a^{l-1}}$ 对应上面的例子中相关联的 w 的值。假设我们的z矩阵对应的反向传播误差是 $\delta{11},\delta{12},\delta{21},\delta{22}$组成的$2\times 2$矩阵，则利用上面梯度的式子和4个等式，我们可以分别写出 $\nabla a^{l-1}$ 的9个标量梯度。

比如对于 $a{11}$ 的梯度，由于在4个等始终，$a{11}$只和$z_{11}$有关，从而我们有：

$$\nabla a_{11} = \delta_{11}w_{11}$$

以此类推，我们可以得到：

$$\begin{align} &\nabla a_{12} = \delta_{11}w_{12}+\delta_{12}w_{11}\\ &\nabla a_{13} = \delta_{12}w_{12}\\ &\nabla a_{21} = \delta_{11}w_{21}+\delta_{21}w_{11} \\ &\nabla a_{22} = \delta_{11}w_{22}+\delta_{12}w_{21}+\delta_{21}w_{12}+\delta_{22}w_{11} \\ &\nabla a_{23} = \delta_{12}w_{22}+\delta_{22}w_{12}\\ &\nabla a_{31} = \delta_{21}w_{21}\\ &\nabla a_{32} = \delta_{21}w_{22}+\delta_{22}w_{21} \\ &\nabla a_{33} = \delta_{22}w_{22}\\ \end{align}$$

　这上面9个式子其实可以用一个矩阵卷积的形式表示，即：

$$\begin{pmatrix}0&0&0&0\\ 0&\delta_{11} & \delta_{12} & 0 \\ 0 & \delta_{21} & \delta_{22}&0\\0&0&0&0 \end{pmatrix}*\begin{pmatrix}w_{22}&w_{21}\\w_{12}&w_{11} \end{pmatrix} =\begin{pmatrix} \nabla a_{11} & \nabla a_{12} & \nabla a_{13} \\ \nabla a_{21} & \nabla a_{22} & \nabla a_{23}\\\nabla a_{31}&\nabla a_{23}&\nabla a_{33} \end{pmatrix}$$

为了符合梯度计算，我们在误差矩阵周围填充了一圈0，此时我们将卷积核翻转后和反向传播的梯度误差进行卷积，就得到了前一次的梯度误差。

因此，我们可以将其一般化：

首先，在DNN中，我们知道$\delta^{l-1}$和 $\delta^{l}$(由后向前推)的递推关系为：

$$\delta^{l-1} = \frac{\partial J(\boldsymbol W,b)}{\partial z^{l-1}} = (\frac{\partial z^{l}}{\partial z^{l-1}})^T\frac{\partial J(\boldsymbol W,b)}{\partial z^{l-1}} = (\frac{\partial z^{l}}{\partial z^{l-1}})^T\delta^{l}$$

因此，要推得到 $\delta^{l-1}$ ，必须要先计算 $\frac{\partial z^l}{\partial z^{l-1}}$

因为 $z^{l-1}$ 和$z^{l}$是前向传播得到的，其关系为：

$$z^l = a^{l-1}*\boldsymbol W^l +b^l = \sigma(z^{l-1})*\boldsymbol W^l+b^l$$

因此：

$$\frac{\partial z^l}{\partial z^{l-1}} = rot180(\boldsymbol W')\odot \sigma'(z^{l-1})$$ $$\delta^{l-1}=(\frac{\partial z^l}{\partial z^{l-1}})\delta^l =\delta^l*rot180(\boldsymbol W')\odot \sigma'(z^{l-1})$$

这里的式子其实和DNN的类似，区别在于对于含有卷积的式子求导时，卷积核被旋转了180度。即式子中的$rot180$，翻转180度的意思是上下翻转一次，接着左右翻转一次。在DNN中这里只是矩阵的转置。那么为什么呢？由于这里都是张量，直接推演参数太多了。我们以一个简单的例子说明为啥这里求导后卷积核要翻转。

已知卷积层的$\delta^l$，推导该层的W,b的梯度

好了，我们现在已经可以递推出每一层的梯度误差$\delta^l$ 了，对于全连接层，可以按DNN的反向传播算法求该层W,b的梯度，而卷积层的W,b需要求出。

在第l层，某个卷积核矩阵 $\boldsymbol W$ 的导数可以表示如下：

$$\frac{\partial J(\boldsymbol W,b)}{\partial W_{pq}^l} = \sum_{i}\sum_j(\delta_{i,j}^la^{l-1}_{i+p-1,j+q-1})$$

假设输入的a是$4\times 4$矩阵，卷积核 $\boldsymbol W$是$3\times3$的矩阵，输出z是$2\times2$的矩阵，那么反向传播的z的梯度误差$\delta$ 也是$2\times 2$的矩阵。

那么根据上面的例子，我们有：

$$\frac{\partial J(\boldsymbol W,b)}{\partial \boldsymbol W_{11}^l} = a_{11}\delta_{11}+a_{12}\delta_{12}+a_{21}\delta_{21}+a_{22}\delta_{22}\\ \frac{\partial J(\boldsymbol W,b)}{\partial \boldsymbol W_{12}^l} = a_{12}\delta_{11}+a_{13}\delta_{12}+a_{22}\delta_{21}+a_{23}\delta_{22}\\ \frac{\partial J(\boldsymbol W,b)}{\partial \boldsymbol W_{13}^l} = a_{13}\delta_{11}+a_{14}\delta_{12}+a_{23}\delta_{21}+a_{24}\delta_{22}\\ (...)$$

最终一共得到9个式子，整理后可得：

$$\frac{\partial J(\boldsymbol W,b)}{\partial \boldsymbol W^l} =\begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44} \end{pmatrix}*\begin{pmatrix}\delta_{11}&\delta_{12}\\\delta_{21}&\delta_{22} \end{pmatrix}$$

从而可以清楚的看到这次我们为什么没有反转的原因。

而对于b,则稍微有些特殊，因为$\delta^l$是高维张量，而$b$只是一个向量，不能像DNN那样直接和$\delta^l$相等。通常的做法是将$\delta^l$的各个子矩阵的项分别求和，得到一个误差向量，即为$b$的梯度

$$\frac{\partial J(\boldsymbol W,b)}{\partial b^l} =\sum_{u,v}(\delta^l)_{u,v}$$

总结CNN

现在我们总结下CNN的反向传播算法，以最基本的批量梯度下降法为例来描述反向传播算法。

输入：m个图片样本，CNN模型的层数L和所有隐藏层的类型，对于卷积层，要定义卷积核的大小K，卷积核子矩阵的维度F，填充大小P，步幅S。对于池化层，要定义池化区域大小k和池化标准（MAX或Average），对于全连接层，要定义全连接层的激活函数（输出层除外）和各层的神经元个数。梯度迭代参数迭代步长$\alpha$,最大迭代次数MAX与停止迭代阈值$\epsilon$

输出：CNN模型各隐藏层与输出层的𝑊,𝑏