损失函数和优化

损失函数

对于线性分类器，常常需要定义一个衡量输出分数好坏的函数——损失函数。然后，我们可以通过这个损失函数，去反推参数，最终让损失函数达到最小值，这就是优化的过程。

我们来举一个例子：

我们令训练集为 ${(xi,y_i )}{i=1}^N$ , $x_i$ 为第i个图片，$y_i\in Z$ 为它的类别标签；$f(\boldsymbol W,\boldsymbol x_i)$ 为第i个图片的输出分数, $\boldsymbol W$ 是权重矩阵，计算公式如下所示：

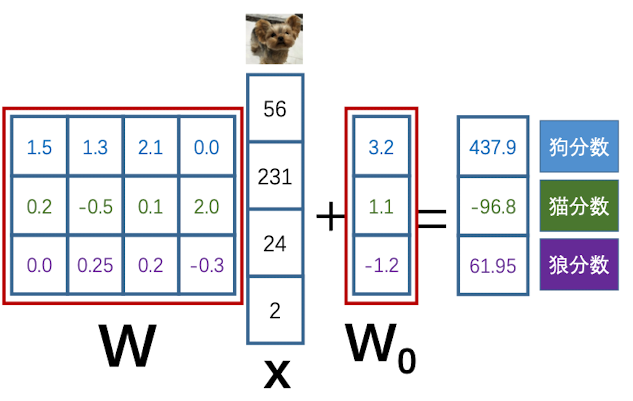
由此，我们可以计算损失函数

第 i 条数据的损失函数 $L_i = l(f(\boldsymbol W,\boldsymbol x_i),y_i)$
训练样本总体损失 $L = \frac{1}{N}\sum_{i=1}^N L_i$

接下来我们来介绍两种线性分类器常用的损失函数

SVM Loss

SVM loss 也叫做 multiclass SVM loss, 首先我们给出定义：

训练集为 ${(xi,y_i )}{i=1}^N$ , $x_i$ 为第i个图片，$y_i\in Z$ 为它的类别标签
我们令 $\boldsymbol s = f(\boldsymbol W,\boldsymbol x_i)$, 即图片i的所有类别分数
然后，我们令 SVM loss为： $Li = \sum{j\neq yi}\max(0,s_j-s{y_i}+1)$
- $s_j$ 代表第 $i$ 张图片在第 $j$ 个分类上的分数
- $s_{y_i}$ 代表这张图片原来类别的分数

为什么要加上1这个常数呢？

答：如果不加上1，想得到0损失的话，那么只要正确类别的分数比其他所有错误类别的分数大就可以了，具体大多少不用管。因此可能出现两个类的分数很接近，正确的类别并不突出。如果加上1以后，至少要让正确类别的分数比其他类别的分数大1。也就是进一步拉大正确类别与错误类别的差距，让模型更加高效。

如果全部正确得对图片进行分类，此时对所有的 $sj$ 肯定是远小于 $s{yi}$ 的。因此此时$L_i = \sum{j\neq y_i}0= 0$

画出图像后我们发现，SVM loss的函数形状就像一个铰链一样，因此也被称为 Hinge Loss

实例计算

现在，我们可以通过一个具体的例子来计算svm loss

	狗图片1	猫图片1	狼图片1	狗图片1
狗	7.9	3.3	-1.1	2.3
猫	5.8	-0.8	3.4	1.5
狼	-1.9	6.5	2.5	4.4

图片1-4的loss:

$\begin{align} &L_1 = \max(0,5.8-7.9+1)+\max(0,-1.9-7.9+1)=0\\ &L_2 = \max(0,3.3-(-0.8)+1)+\max(0,6.5-(-0.8)+1)=13.4\\ &L_3 = \max(0,-1.1-2.5+1)+\max(0,3.4-2.5+1)=1.9\\ &L_4 = \max(0,1.5-2.3+1)+\max(0,4.4-2.3+1)=3.3\\ \end{align}$

总的loss:

$L = \frac{1}{N}\sum_{i=1}^N L_i = \frac{1}{4}(0+13.4+1.9+3.3) = 4.65$

QA

Q : 如果输出分数发生微小改变(比如$\pm0.001$)，对SVM loss的计算会造成什么影响

A : $sj-s{y_i}<-1$ 时，没有影响。反之，会略为改变损失函数的值

Q: SVM 损失函数的最大值和最小值分别为多少

A: 最小值为0(全分对)，最大值为正无穷(理论上)，可用于代码正确性检查

Q: 加入初始化 $\boldsymbol W$ 接近0，导致所有输出分数都$\approx 0$,那么$L_i$ 约等于多少？

A: 由公式可得：$Li = \sum{j\neq y_i}\max(0-0+1)$ 。因此此时 $L_i$ 的分数为 $C-1$， $C$ 为类别数，这里为 $3-1=2$ 。此问题也可以用于代码检测

Q: 加入去掉$j\neq y_i$ 的限制，损失函数该如何变化？

A: 损失函数会增加1

Q: 加入在$Li$中使用$\max(s_j-s{yi}+2)$ 代替 $\max(s_j-s{y_i}+1)$ ，有什么影响？

A: 不会改变分类的结果，SVM loss 只关注输出分数之间的差异，这里的常数只起到scale参数的作用，会导致权重矩阵的变化。

Q: 加入 $\boldsymbol W$ 使得 $L=0$ (完美)，轻微 $\boldsymbol W$ 是否唯一？

A: 不唯一，因为$\boldsymbol W\times c $ 也可以使得$L=0$, $c$ 为任意正整数。因为权重矩阵的整体放大是不会影响到结果的。我们可以通过添加正则项来选取更好的 $\boldsymbol W $ ,增强模型的泛化能力

Softmax Loss

第二个常用的损失函数是 softmax loss(cross-entropy loss). 用这个损失函数构造的分类器也被称为是Softmax分类器(多类别逻辑回归)

我们同样给出定义：

训练集为 ${(xi,y_i )}{i=1}^N$ , $x_i$ 为第i个图片，$y_i\in Z$ 为它的类别标签
我们令 $\boldsymbol s = f(\boldsymbol W,\boldsymbol x_i)$, 即图片i的所有类别分数
softmax loss ：
- 同样的，$s_{y_i}$ 代表这张图片原来类别的分数
- $s_j$ 代表第 $i$ 张图片在第 $j$ 个分类上的分数

如果是正确分类的话，$s{y_i}$是特别大的，因此 $(\frac{e^{s{y_i}}}{\sum_j e^{s_j}})$ 接近于1，$L_i$ 就接近于0

原理

交叉熵

首先我们要了解交叉熵的概念

我们知道熵(entropy) 是用来衡量概率分布Q的不确定性的:

$H(Q) = -\sum_i q_i \log q_i$

那么交叉熵(Cross-entropy) 则是用来衡量概率分布P服从概率分布Q的不确定性,就是把对数后面的q改为p：

$H(Q,P) = -\sum_{i}q_i\log p_i$

比如说这里有个例子：

	晴天	多云	下雨
真实天气	50%	30%	20%
天气预报	40%	30%	30%

可以计算真实天气的不确定性：

$H(\text{真实}) = -(0.5\log(0.5)+0.3\log(0.3)+0.2\log(0.2))=0.45$

当只有一种天气的时候，可知： $H(真实) = -(1\log 1) = 0$

利用交叉熵，可以计算天气预报服从真是天气的不确定性：

$H(真实,预报) = -(0.5\log(0.4)+0.3\log(0.3)+0.2\log(0.3)) = 0.46$

正常情况下，我们是利用 KL 散度(相对熵)来衡量两者分布的差异性：

$D_{KL} (Q||P) = H(Q,P)-H(Q) = -\sum q_i\log p_i-(-\sum_i q_i\log q_i) =\sum_i q_i\log\frac{q_i}{p_i}$

但在计算softmax loss时，我们只考虑交叉熵的计算即可。因为在图像分类场景下，真实的分类是确定的, $H(\text{真实})=0$ , 所以说交叉熵和KL散度在图像分类情况下是等价的

定义

首先，我们可以将分数通过 softmax 函数转换为概率，即：

$\begin{align} &\text{分数}: \boldsymbol s = f(\boldsymbol W,\boldsymbol x_i)\\ &\text{概率}: P(y=k|x_i) = \frac{e^{s_k}}{\sum_j e^{s_j}} \end{align}$

接着，我们利用交叉熵，计算第i个图片的损失：

$L_i = -\log P(y=y_i|x_i) = -\log (\frac{e^{s_{y_1}}}{\sum_j e^{s_j}})$

其中，$y_i$ 代表正确的标签

实例计算

我们还是那 SVM loss的那个例子来计算，得到了分数以后我们先计算预测的每个类别的概率，得到蓝色框框。

然后通过计算cross entropy 来得到 $L_1$

QA

Q: 如果有输出分数发生微小改变(比如 $\pm 0.1$)，损失函数是否发生改变？

A: 使得，正确类别和错误类别输出分数差距越大，损失函数就越小

Q: 损失函数$L_i$ 的最大值和最小值分别是多少？

A: 最小值为0(理论上)，最大值为正无穷(理论上)

Q: 加入初始化 $\boldsymbol W$ 接近0，导致所有输出分数都$\approx 0$ ，那么$L$ 约等于多少？

A: $Li = -\log (\frac{e^{s{y_1}}}{\sum_j e^{s_j}})$ , 当输出分数都约等于0的时候，$L_i = -\log(1/C)=\log C$, 其中$C$为类别数，这里为 $\log 3$

两类分类器的对比

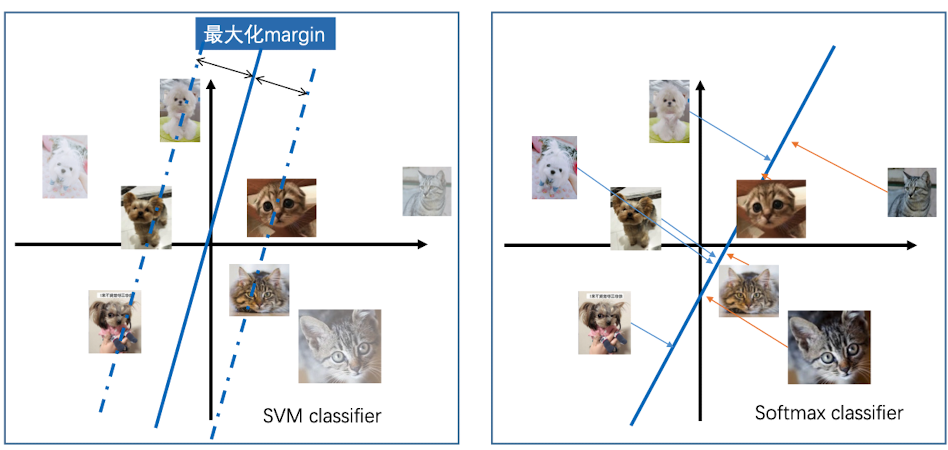
为什么左边的是SVM分类器，右边的是Softmax分类器？

因为SVM有一个boundary，而且并不关注所有类别到这个分类器的距离。他只要求其他类别比正确类别的分数小于1(boundary)即可。因此我们看到，左边的分类器目标是最大化 margin即可，并不需要计算每张图片到中心的距离。

而Softmax分类器，每个图片都参与了关于loss的计算。我们看到右边的分类器，需要一一计算每张图片到超平面的距离。

正则化

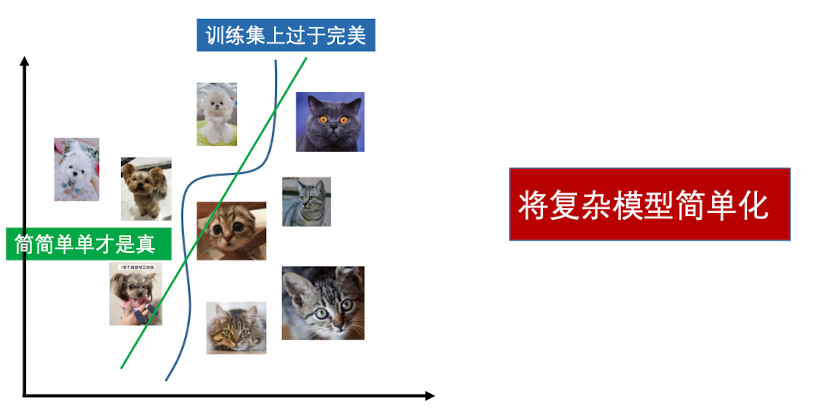
正则项的意义：1. 缩小参数空间 2. 调整参数偏好的分布 3. 提高模型泛化能力。我们希望的分类器是下面这张图中的绿色线条。因为蓝色曲线已经过拟合了，在其他数据集上的表现会比较糟糕。

怎么正则化呢？我们可以修改 loss 函数

$L(\boldsymbol W) = \frac{1}{N}\sum_{i=1}^N l(f(\boldsymbol W,x_i),y_i) +\lambda R(\boldsymbol W)$

前一部分是数据损失，后一部分是正则项，用来防止模型过拟合训练集。其中$\lambda$是超参数，代表正则化的强度；正则项 $R(\boldsymbol W)$ 有 L1正则，L2正则以及两种混合起来的正则。

L1正则化

L1正则就是将每个权重的绝对值累加。

$L1: \sum_k\sum_l|w_{k,l}|$

L2正则化

L2正则是将每个权重求平方之后累加：

$L2: \sum_k\sum_l|w_{k,l}^2|$

此外还有Dropout, Batch normalization, Stochastic depth 和 Fractional pooling 等方法

L1 vs L2

我们给个例子：

$\begin{align} &x= [1,1,1]\\ &\boldsymbol W_1 = [1,0,0]\\ &\boldsymbol W_2 = [0.3,-0.1,0.8]\\ &\boldsymbol W_1^T x = \boldsymbol W_2^T x = 1\\ \end{align}$

使用$L1$ 正则化，对于$\boldsymbol {W_1,W_2}$，可得：

$\boldsymbol W_1 : \sum_{k}\sum_l|\boldsymbol W_1| = 1\\ \boldsymbol W_2 : \sum_{k}\sum_l|\boldsymbol W_2| = 1.2$

使用$L_2$ 正则化，可得：

$\boldsymbol W_1 : \sum_{k}\sum_l|\boldsymbol W^2_1| = 1\\ \boldsymbol W_2 : \sum_{k}\sum_l|\boldsymbol W^2_2| = 0.74$

我们看到，$L_1$ 偏向于是参数集中在少数输入像素上

$L_2$ 偏向于是参数分布在所有像素上

损失函数计算流程

初始化$\boldsymbol W$
计算 $s= f(\boldsymbol W,x_i)$
选择损失函数，计算 $L总 = \frac{1}{N}\sum{i=1}^N L_i+\lambda R(\boldsymbol W)$ 得到 Total Loss
通过优化算法，修改原来的参数矩阵 $\boldsymbol W$
重复2-4, 直到收敛

图像特征抽取

线性分类器是可以应用于图像的，如果直接用像素点来计算，效果其实是很差的。因此往往需要对原始像素做特征抽取，利用抽取的特征来训练模型，以提高预测性能。如下所示：

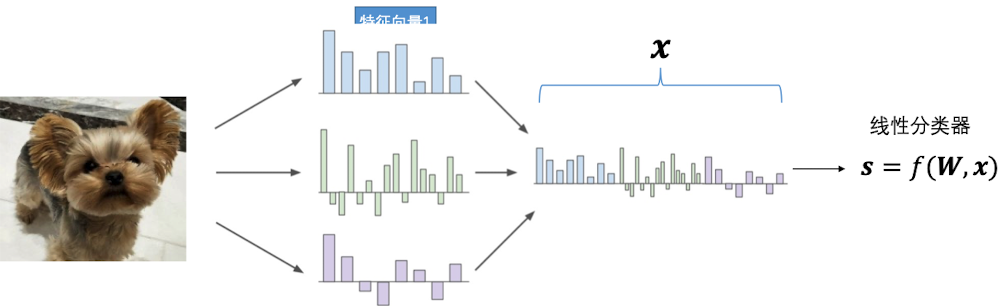
在深度神经网络(DNN)中的前几层，其实就是一个提取图像特征的过程。那么在线性分类器中，我们有什么方法呢？

Hue Histogram

建立色相哈希表
哈希每个像素值，并计算每个key中像素的个数
将哈希结果作为模型输入

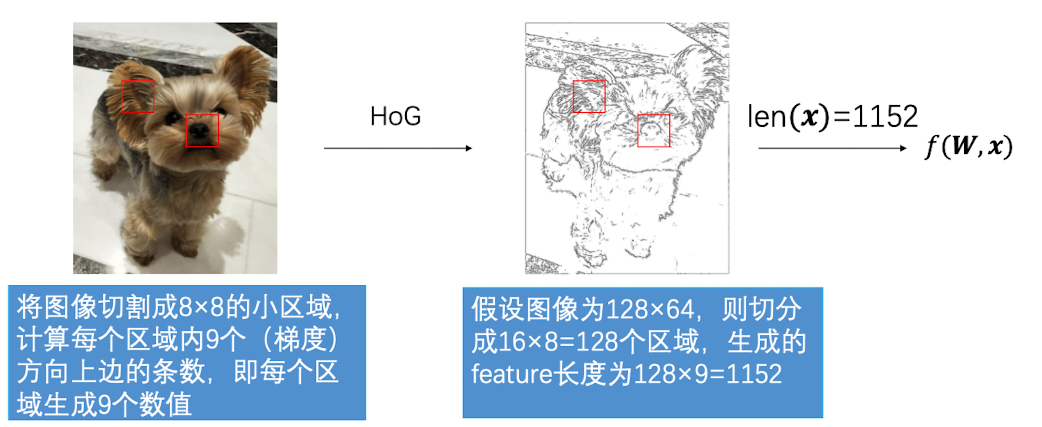
HoG

HoG 的全称是：Histogram of Oriented Gradients(方向梯度直方图)

优化

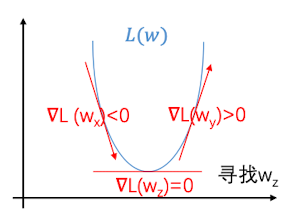
我们的目标是最小化损失函数 $L(\boldsymbol W)$ ，因为这时候预测的最接近于真实值。

假设只有一个参数$w$：

导数 $\frac{dL(w)}{dw} = \lim\limits_{h\rightarrow 0}\frac{L(w+h)-L(w)}{h}$ 代表$L$ 在$w$ 的切线斜率，即 $L(w)$ 在该店的变化速率及方向
因此沿导数反方向微调w即可减小$L(w)$

如下图所示：

在多维情况下，即$\boldsymbol W$ 为向量

偏导数$[\frac{\partial L(\boldsymbol W)}{\partial w1},\frac{L(\boldsymbol W)}{\partial w_2},\cdots,\frac{L(\boldsymbol W)}{\partial w_n}]$ 代表L 在 $\boldsymbol W$ 处沿每个维度的变化速率和方向，称为梯度(gradient).记为 $\nabla{\boldsymbol W}L$ 或者 $grad(L(\boldsymbol W))$
$\nabla_{\boldsymbol W}L$ 和方向向量$\boldsymbol v$ 的点积记为该方向的斜率(方向导数) ,公式如下：
$\nabla_{\boldsymbol W}L\cdot v = |\nabla_{\boldsymbol W}L ||v|\cos\theta$
那么，当$\cos\theta =1$ 的时候，达到最大值，即$\boldsymbol v$ 和 $\nabla{\boldsymbol W}L$ 同方向，所以负梯度 $-\nabla{\boldsymbol W}L$ 代表 $L$ 下降最快的方向(最陡峭)。
沿 $-\nabla_{\boldsymbol W}L$ 方向微调$\boldsymbol W$ 即可快速减小 $L(\boldsymbol W)$
$\boldsymbol W_{new} = \boldsymbol W -\lambda\nabla_{\boldsymbol W}L$
超参数$\lambda $ 为 step size 或 learning rate，代表梯度下降的快慢，如果太小会导致梯度下降过慢，算法效率低下；太大会导致找不到梯度最优点。在计算机视觉-神经网络的训练中，我们还会仔细探讨这个问题。

数值梯度

数值梯度就是根据导数的定义去求得梯度。比如说关于权重向量$\boldsymbol W$，手动计算梯度：

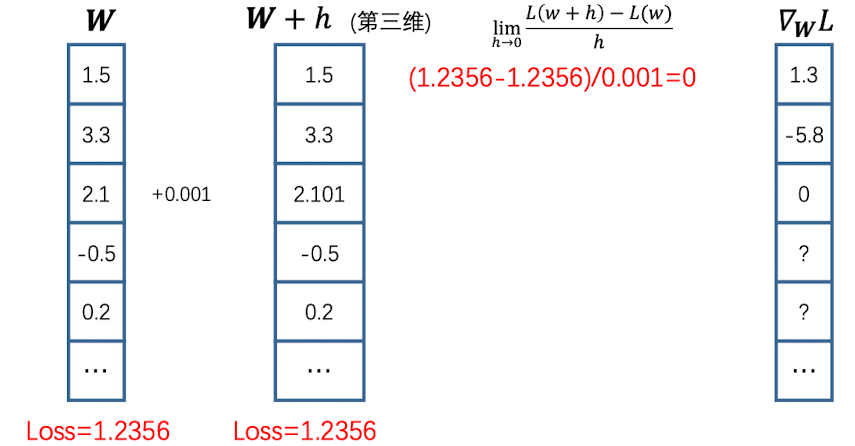
但这样计算开销太大，需要遍历所有参数，并计算损失函数和梯度。显然，当参数过多时采用这种方法是不可行的

解析梯度

我们可以对损失函数求偏导，编写梯度公式，以此来直接计算梯度.即：

$\nabla_{\boldsymbol W}L = [\frac{\partial L(\boldsymbol W)}{\partial w_1},\frac{L(\boldsymbol W)}{\partial w_2},\cdots,\frac{L(\boldsymbol W)}{\partial w_n}]$

Hinge Loss

http://ningyuwhut.github.io/cn/2018/01/gradient-of-svm-loss/

实现非向量化的svm还是比较简单的，其实只要两层训练即可，

第一层循环遍历每个样本,第二层循环遍历每个类;

在第二层循环中需要完成两件事: 1.计算当前类的loss， 2.同时计算对当前类和样本正确类的梯度。

当$i\neq y_j$ 的时候，我们需要对当前类的梯度进行修改

$\frac{d L_i}{d w_j} = \mathbb 1(w_j^Tx_i-w^T_{y_i}x_i+\Delta>0)\begin{bmatrix}x_{i1}\\x_{i2}\\\vdots\\ x_{iD} \end{bmatrix} \\ =\mathbb 1(w_j^Tx_i-w^T_{y_i}x_i+\Delta>0) x_i^T$

类似的，对于正确类的样本，我们这么更新：

$\frac{d L_i}{d w_{y_j}} = -\sum_{j\neq y_i}\mathbb 1(w_j^Tx_i-w^T_{y_i}x_i+\Delta>0)\begin{bmatrix}x_{i1}\\x_{i2}\\\vdots\\ x_{iD} \end{bmatrix} \\ =-\sum_{j\neq y_i}\mathbb 1(w_j^Tx_i-w^T_{y_i}x_i+\Delta>0) x_i^T$

def svm_loss_naive(W, X, y, reg):
		dW = np.zeros(W.shape)  # initialize the gradient as zero
                            # compute the loss and the gradient
    num_classes = W.shape[1]
    num_train = X.shape[0]
    loss = 0.0
    final_result = []
    for i in range(num_train):# 循环每个样本
        scores = X[i].dot(W)
        correct_class_score = scores[y[i]]
        for j in range(num_classes): # 循环每个类别
            if j == y[i]: # 如果该样本属于当前类，continue
                continue
            margin = scores[j] - correct_class_score + 1  # 计算svm loss
            if margin > 0:
                loss += margin # loss是累加
                dW[:, j] += X[i].T  # 更新当前类的梯度
                dW[:, y[i]] += -X[i].T  # 更新正确类的梯度

    # Right now the loss is a sum over all training examples, but we want it
    # to be an average instead so we divide by num_train.
    loss /= num_train #需要除以样本数量
    dW /= num_train
    # Add regularization to the loss.
    loss += reg * np.sum(W * W) # 需要加上正则项
    dW += reg * W
    return loss, dW

Cross entropy Loss

https://www.cnblogs.com/makefile/p/softmax.html

和SVM loss一样，我们同时要有两个循环，第一层循环遍历每个样本,第二层循环遍历每个类;我们要分两种情况进行讨论，当当前样本属于当前类的时候，当当前样本不属于当前类的时候。

首先，我们知道每个样本的softmax loss是这么计算的：

$L_i = -\log(\frac{e^{f_{y_i}}}{\sum_j e^{f_j}})$

其中，f 即计算来的分数：

$f_{y_i} = w_{y_i}^T x\\ f_j = w_j^Tx$

所以，如果我们要计算损失函数关于参数矩阵$w$ 的导数，需要用到高链式法则：

$\frac{dL}{dw} = \frac{dL}{df}\cdot\frac{df}{dw}$

其中，$\frac{df}{dw} = x$, 我们主要来看 $\frac{dL}{df}$

当 $j\neq y_i$ 时

我们就不需要计算正确分类时的损失，只需要针对分母中的错误项求偏导,因为分母中也包含正确项系数，因此在求导的时候需将其提出，以此计算错误分类时的损失

$\begin{align} \frac{dL_i}{df} &= \Bigg(-\log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}}) \Bigg)' = -\frac{\sum_je^{f_j}}{e^{f_{y_j}}} \cdot e^{f_{y_j}}(\frac{1}{\sum_j e^{f_j}})'\\ &=-\frac{\sum_je^{f_j}}{e^{f_{y_j}}} \cdot e^{f_{y_j}}\cdot(-e^{f_{y_j}})\cdot\frac{1}{(\sum_j e^{f_j})^2}\\ &=\frac{e^{f_{y_i}}}{\sum_je^{f_j}}\\ \end{align}$

当 $j == y_i$时

此时，我们需要对分子求偏导，来计算正确类的损失

$\begin{align} \frac{dL_i}{df} &= \Bigg(-\log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}}) \Bigg)' = -\frac{\sum_je^{f_j}}{e^{f_{y_j}}} \cdot (e^{f_{y_j}}\frac{1}{\sum_j e^{f_j}})'\\ &=-\frac{\sum_je^{f_j}}{e^{f_{y_j}}} \cdot [{e^{f_{y_i}}(\sum_j e^{f_j})^{-1}+e^{f_{y_i}}\cdot\frac{(-1\cdot e^{f_{y_i}})}{(\sum_je^{f_j})^2}}]\\ &=\frac{e^{f_{y_j}}}{\sum_j e^{f_j}}-1 \\ \end{align}$

现在，我们已经计算了两种情况下的梯度，我们可以用示性函数将其统一起来：

$\frac{dL_i}{df} = \frac{e^{f_{y_j}}}{\sum_j e^{f_j}}- \mathbb 1(j==y_i)$

因此，

$\frac{dL}{dW_i} = (\frac{e^{f_{y_j}}}{\sum_j e^{f_j}}- \mathbb 1(j==y_i))x$

Softmax_loss_naive方法代码如下：

# 第一层循环，遍历样本
for ii in range(num_train):
  current_scores = scores[ii, :]
 
  # Fix for numerical stability by subtracting max from score vector.
  # important! make them range between infinity to zero
  shift_scores = current_scores - np.max(current_scores)
 
  # Calculate loss for this example.
  loss_ii = -shift_scores[y[ii]] + np.log(np.sum(np.exp(shift_scores)))
  loss += loss_ii
# 第二层循环，遍历类 		
  for jj in range(num_classes):
    softmax_score = np.exp(shift_scores[jj]) / np.sum(np.exp(shift_scores))
		# 分两类进行权重矩阵的更新
    if jj == y[ii]:
      dW[:, jj] += (-1 + softmax_score) * X[ii]
    else:
      dW[:, jj] += softmax_score * X[ii]
      
   # Average over the batch and add our regularization term.
loss /= num_train
loss += reg * np.sum(W*W)
 
# Average over the batch and add derivative of regularization term.
dW /= num_train
dW += 2*reg*W

梯度下降

其实梯度下降也有很多种方法，除了正常的梯度下降(GD) 之外，还有批量梯度下降法(Batch Gradiant Descent, BGD) 和随机梯度下降(Stochastic Gradiant Descent, SGD)

这里主要拿 GD和SGD做一个比较

GD

优势：每次迭代 loss 下降很快
劣势: 一次迭代需要遍历所有数据，并容易陷入局部最小值，导致梯度无法更新

SGD

随机梯度下降是说，每次选取一个sample集(minibatch，一般大小为32/64/128/256). 然后，利用sample集上的损失来计算近似梯度，进行梯度下降。

优势: 迭代更新速度快，并且往往因为 mini-batch含有噪声而避开 local minima
劣势: 每次迭代的 loss 下降很漫

由于数据量较大，训练深度神经网络(DNN) 的时候基本使用SGD，以及其他性能更佳的优化方法。