计算机视觉-图像分类
在上一节课我们主要讲了计算机视觉的最主要的几个任务:图像分类、定位+分割、目标检测、语义分割、实例分割。现在我们来着重看计算机视觉中最基础的任务——图像分类。有了图像分类,我们才可以做定位+分割、目标检测等更高阶的任务。
图像分类任务
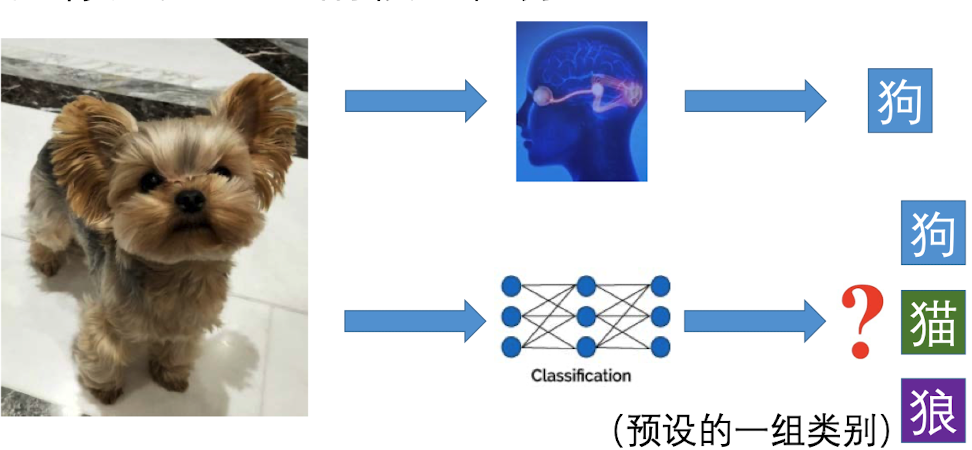
图像分类任务,顾名思义,就是对于一张输入的图片,通过某种方法让计算机算出这张图片属于什么类型。比如说一张狗图,对于人脑而言,可以很简单的辨别出它是狗;但是对计算机来说,它只能给出一组概率,比如说狗的概率0.8, 猫的概率0.1,狼的概率0.1,最终判断它是狗
对计算机的挑战
语义鸿沟
其实,这任务对计算机来说是比较困难的,因为涉及到语义鸿沟,对于计算机来说,图片对他来说只是有一个一个像素组成的,每个像素都是一组 $[0,255]$的数字。如下所示:

尺度、视角差异
当对一个物体的拍摄距离或者拍摄角度产生变化的时候,对人脑而言可能很快就能意识到只是尺度发生了变化,但是物体还是一样的。但是对于计算机来说,他所看到的像素点可能发生了天翻地覆的变化,因此这也是一大难题
类内差异
因为狗有很多品种,不同品种的狗可能样貌、体型、颜色会有很大的变化,大脑可以马上明白过来这虽然是不同的品种,但都属于狗这一类。但对于计算机来说,就可能将它们划归为不同的类去了。
其他

传统方法
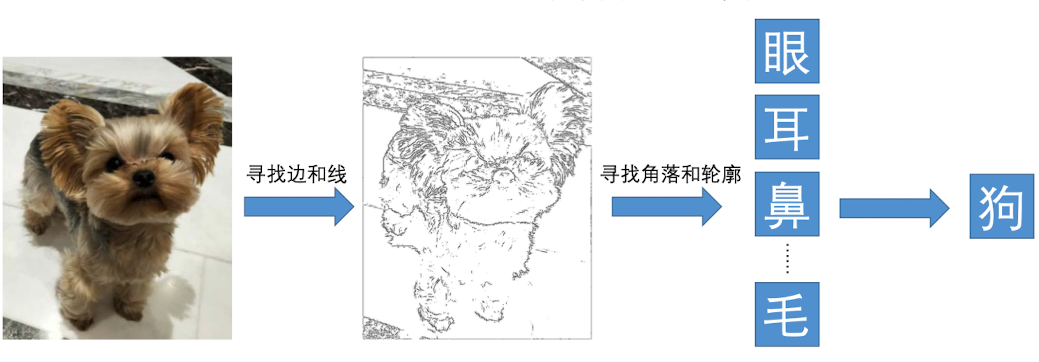
传统方法是利用边缘检测方法,将图片转换成边和线。然后,我们需要在这些边和线中找出可以被捕获到的特征,比如眼睛、鼻子、毛发等。根据这些特征去判断图片中的物体是否属于狗。
但是这种算法,存在很大的缺陷:
- 鲁棒性很差,对于不同的光线、角度、背景,可能会失效
- 可扩展性很差(延展性较差),需要为每一种物体设计专门的算法。
- 需要我们 Hard code
数据驱动的方法
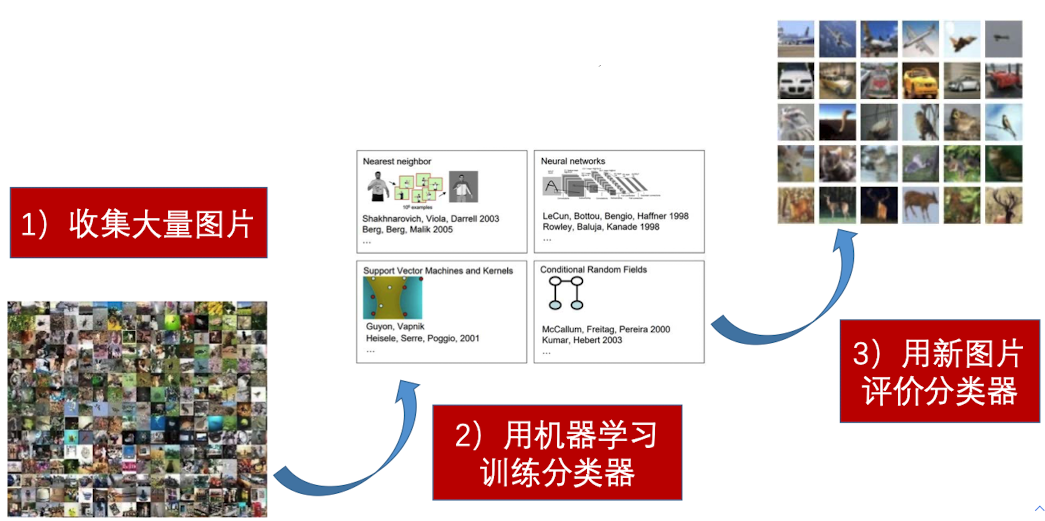
传统方法的局限性迫使我们找到高效的,基于数据驱动的方法。构建一个模型的的基本步骤如下:
NN(Nearest Neighbor)
我们 现在来介绍第一个算法:NN。 它是一个香草分类器,也就是最简单的分类器。
在训练阶段,它会存储下所有的图像和标签。在测试阶段,对于每一个样本,都会遍历所有的类,计算样本和类之间的距离,然后使用距离最近的图像的标签来预测新图像的标签。
我们常常用的是 L1距离(曼哈顿距离)
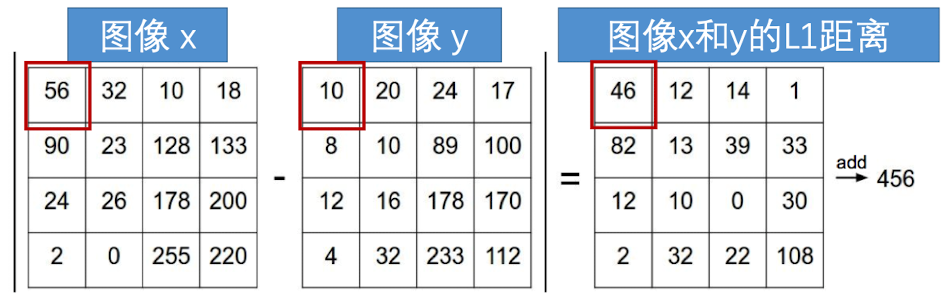
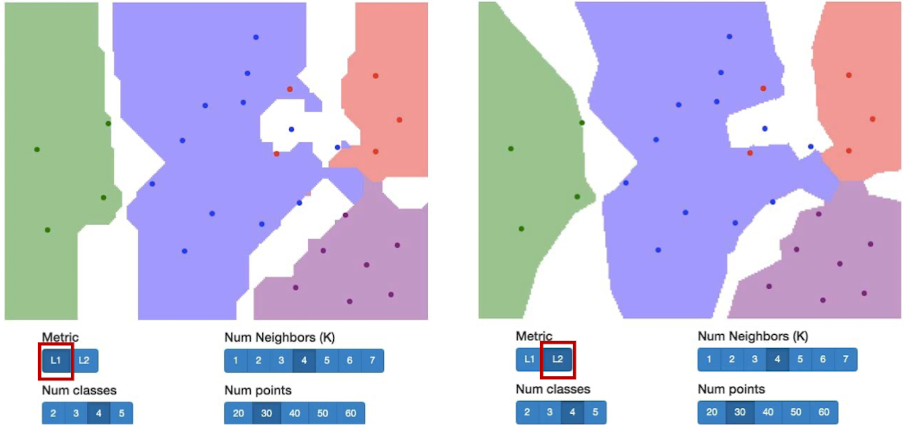
效果展示,我们根据像素之间的距离将其分为了不同的颜色,代表了不同的类。我们发现,几个红点很明显被紫色包围了,但是分类器还是将其分成了红色的点。这些离群值会导致整个分类器并不是很稳定。
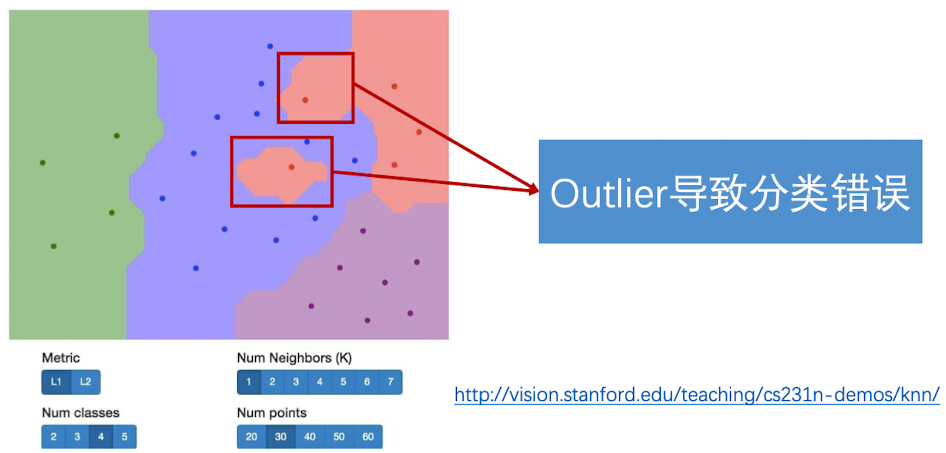
我们发现,
KNN
KNN 和NN 不同,NN是只计算最近的邻居是谁,而 KNN 是计算K个距离最近的邻居,并从中找到占据多数的类别作为预测结果
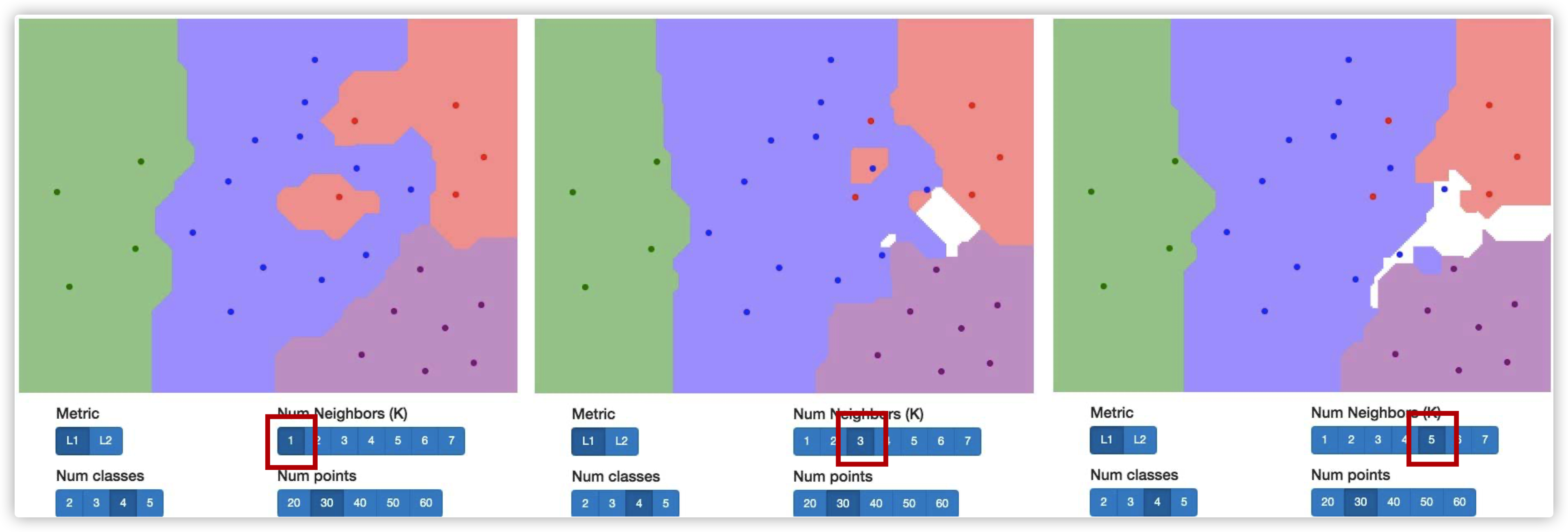
我们发现,使用KNN的方法中间会有空白部分。这可能是因为,这一块区域里。到相邻几类的距离事项等的,因此分类器没办法判别到底是哪一类。
距离选择
除了L1距离,我们还可以用L2距离(欧氏距离):
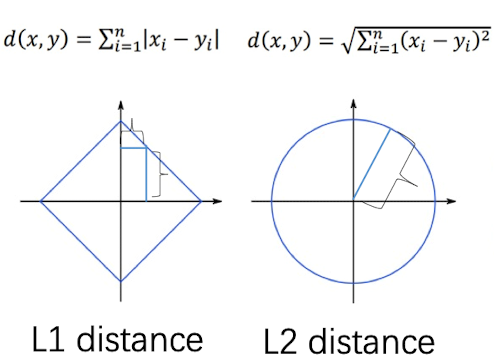
超参数
那么,对于K-NN中的超参数K,我们又该怎么去选择呢?
- 猜想1:我们可以是模型在整个数据集上表现最好
这是不行的,这会导致超参数在现有数据集上完美分类,造成过拟合。举一个极端的例子,我们如果去k=1,那么对于所有点来说,都属于同一类,那么k=1在这个情况下是完美的超参,但这显然是很荒唐的
- 猜想2:使模型在测试集上表现最好
这也是不行的,因为这就相当于看到了答案反推模型,我调参的目的就是服务于测试集,这会污染我们的模型,是一种作弊行为。可想而知,用这种方法做出来的模型在测试集上会有很好的表现,但是,在其他数据集上的表现会很拉跨。
- 猜想3:如下图所示

我们将数据划分为训练集、验证集和测试集,三者隔离开来。我们在验证集上找到最好的表现,然后将模型应用于测试集,查看最终表现。这样test中的数据就不会对算法本身造成影响,在接触到测试集前,模型对其一无所知,这样才能”毫无干扰“得做出预测。
- 猜想4:交叉验证(cross validation), 这是在第三种方法基础上的衍生,我们可以将数据集拆分成更多块,并获得更好的泛化性能。如下图所示,我们将每一块成为一个Fold。对于每一个Fold,我们都会有一次机会把它作为验证器,其他Folds作为训练集,对于每一次训练,都会获得一组最好的超参数组合。最后我们取其所长,获得最后的超参搭配
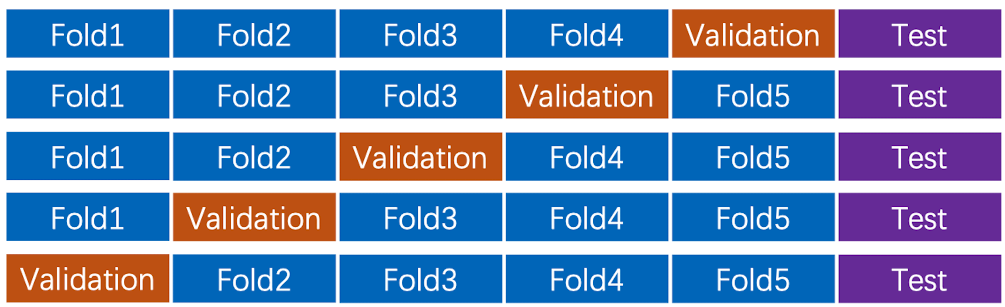
但是对于大型数据和深度学习较少使用这种方法。因为训练起来会比较麻烦。
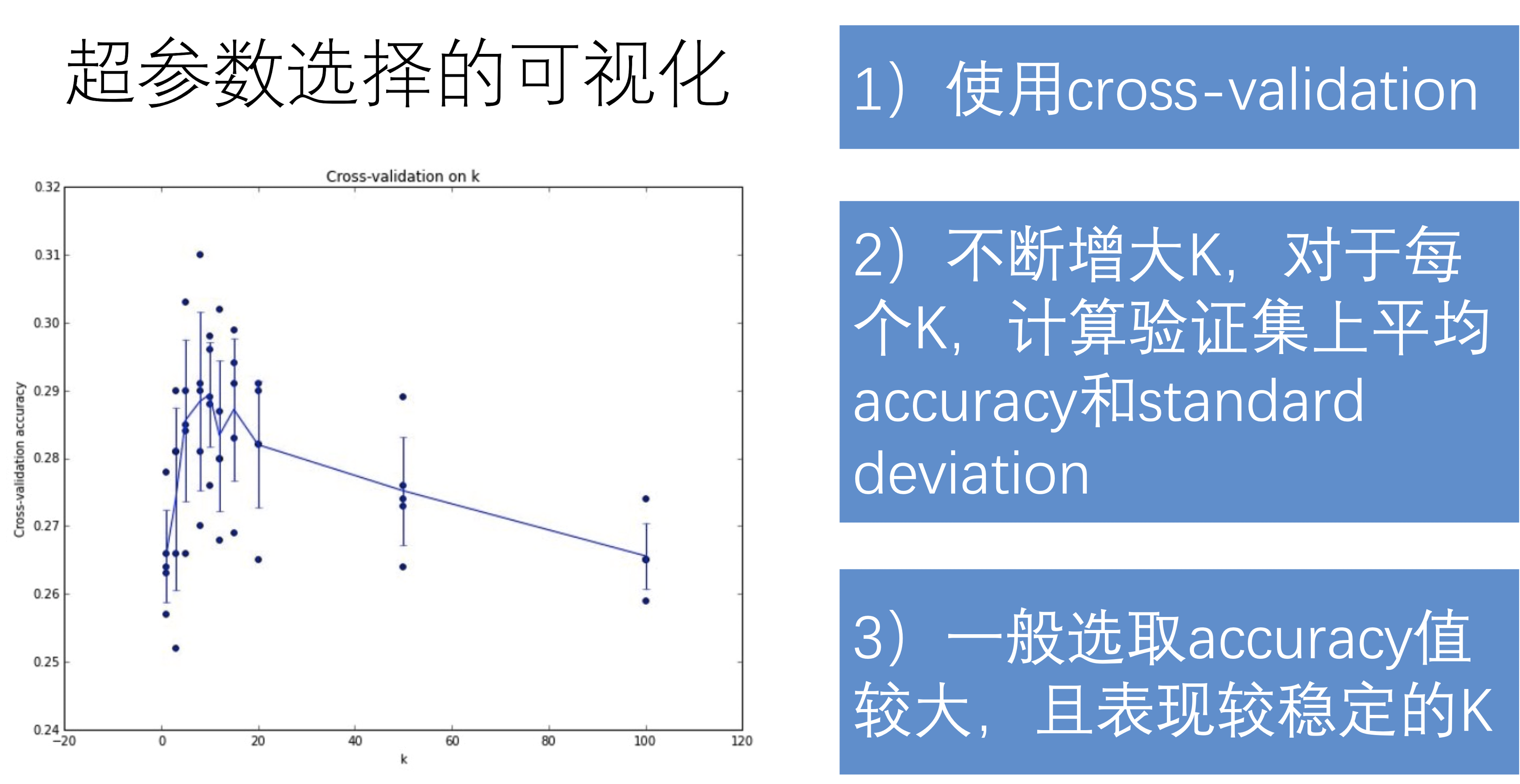
超参选择可视化
小结
(K)NN 方法的优点很简洁明了:简单
同时,KNN也存在很多缺点:
训练阶段时简单的标签记忆
- 预测效率低下(20%左右),训练时需要$O(N)$的复杂度
- lazy learner,在训练阶段并不会做任何泛化;而图片分类需要具备一定的泛化能力的分类器
像素距离和图像信息之间存在语义鸿沟
- 图像像素相近(颜色相近)并不等于 图像包含的信息接近
对训练集数据分布要求会很高、
- 首先我们要知道,只要点够多,KNN在训练的时候可以近似于任何曲线(可以推广到平面)。但是点不够平均的话,KNN模拟出来的函数会误差很大。
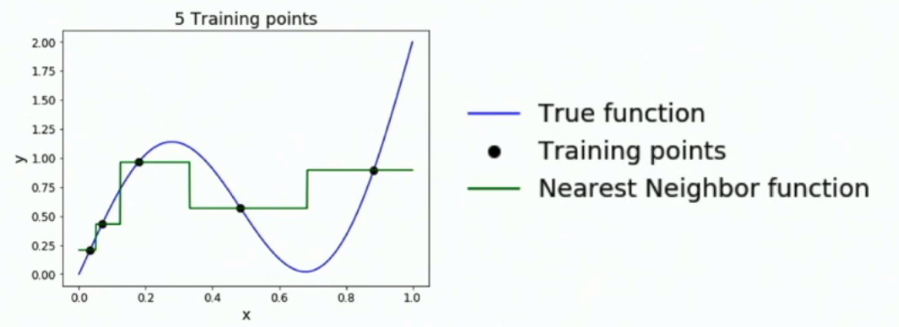
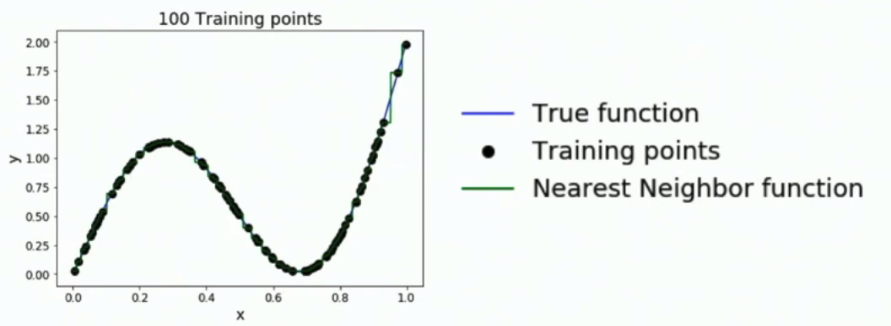
- 为了提高模型预测的准确率,我们的训练集需要在整个像素空间中均匀分布,导致维度诅咒(curse of dimensionality)。也就是说只要增加一个维度,就需要对数据集扩大指数倍才能满足训练的需要。
Linear classifier

当然,线性分类器也有很难应用的数据分布: