数据科学与算法-流算法补充

Posted on
Words count in article: 2.7k | Reading time ≈ 10

流算法补充

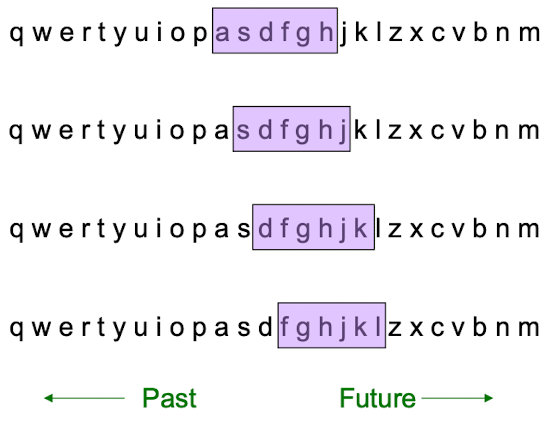
Queries over a sliding window

在第五章流算法中，我们讲了一些数据挖掘算法：Basic Count Sketch，Count Sketch 和 Count-min Sketch。当时我们提了一嘴滑动窗口模型，但没有细讲。现在我们来对这个数据流模型做一个补充

比如说举一个Amazon的例子，数据流是亚马逊上的订单，数据流的值是0-1，其中，0代表数据流不包含某个商品，1代表数据流包含某个商品，我们希望统计在过去的n笔订单中，有多少订单包含商品 X(统计1的个数)

朴素方法

要计算数据流中过去 k 个bits 有多少个1(k<窗口大小N)，一个朴素的想法是：维持一个计数器

每当有一个新的bit进来，就需要抛弃一个bit

  • 如果进来或抛弃的bit 是 0，那么什么都不用做
  • 如果进来的bit 是1，那么计数器+1
  • 如果进来的bit 是0，那么计数器-1

这个算法的空间复杂度是$O(n)$,因为我们要时刻保持窗口中的数据；时间复杂度为$(O1)$

那么，如果N 等于 1 billion 会怎么样？我们肯定不能将其全部保存下来，因此我们可以采用一个近似算法。

尝试1

我们尝试维护两个计数器：

S: 维护数据流中的1的个数

Z: 维护数据流中的0的个数

因此我们可以用这两个计数器的值，结合窗口大小去估算窗口内1的数值:$ = N\cdot \frac{S}{S+Z} $

但是这样又不对，因为采用这种方法，随便你窗口化到哪，对1的个数的估算都是不会变的。也就是说，加入之前数据流 1和0的比值为0.8：0.2，那么相当于假设之后来的数字也是0.8:0.2，但现实生活中事件发生的概率是不停变化的，因此是不可行的。

DGIM 算法

因此我们提出了一种更高效的解决方法：DGIM算法

在DGIM算法中，我们对于一个长度为N的数据流，我们存储 $O(\log^2 N)$ 个 bits, $O(\log_2(N))$个桶 ，相当于一个亚线性的算法，而且我们要得目标的估计偏差不能超过 50%，也就是说，假设1的出现次数是100，那么我们的估计必须落在 50~150之间

首先假设对于二进制流，其中每个位可以用一个时间戳（timestamp）标志该位进入流的时间（对于大小为N的滑动窗口，该时间戳可以用O(logN)位表示）。

DGIM算法利用桶（bucket）对滑动窗口进行划分，每个桶保存以下信息：

  • 桶的最右边位即最后进入流的位的时间戳；

  • 桶的大小，即桶中1的个数，该数目位2的幂。

    对于以上信息，保存时间戳需要logN的空间，保存桶的大小需要 logN 的空间。

使用桶对滑动窗口进行划分时遵循以下5条规则：

  • 桶最右边的位必须是1；
  • 1个位最多属于1个桶；
  • 每种大小的桶有1个或者两个（从1到最大的桶的大小）；
  • 每个桶的大小是2的幂；
  • 桶的大小从右到左非降序排列；

DGIM算法中数据结构的更新：

  • 每一个新的位进入滑动窗口后，最左边一个位从窗口中移出（同时从桶中移出）；如果最左边的桶的时间戳是当前时间戳减去N（也就是说桶里已经没有处于窗口中的位），则放弃这个桶；
  • 对于新加入的位，如果其为0，则无操作；否则建立一个包含新加入位的大小为1的桶；
  • 由于新增一个大小为1的桶而出现3个桶大小为1，则合并最左边的两个桶为一个大小为2的桶；合并之后可能出现3个大小为2的桶，则合并最左边两个大小为2的桶得到一个大小为4的桶……依次类推直到到达最左边的桶。

我们用一个直观的例子来展现：

  • 这是我们的初始数据流：

我们看到现在一共有长度为1的桶2个；长度为2的桶1个；长度为4的桶2个；长度为8的桶2个; 长度为16的桶1个，但是一部分在滑动窗口外，因此显示不出

  • 当到达了一个新的 1 ，如下图

我们发现现在长度为1的桶有3个，超出了2个，因此要向上合并

  • 当到达了三个数据 101

这时候，我们发现，合并了两个长度为1的桶，有3个长度为2的桶；合并了两个长度为2的桶，就有3个长度为4的桶；合并了两个长度为4的桶，有三个长度为8的桶。

最终，我们得到下图：

估计

最后，我们该怎么利用计数桶去怎么去估计1的个数？

  1. 我们可以叠加滑动窗口中的桶的大小，除了最后一个桶，因为最后一个桶有一部分已经滑出窗口外了
  2. 因此，我们可以近似地认为最后这个桶(也是最大的桶)的大小变为原来的$\frac{1}{2}$ ,并加到结果中去

用上面那个例子来估计，滑动窗口中，对1的个数的估计为：1+2+4+8+16+16/2 = 39个

因为一共有 $O(logn)$ 个桶，因此算法的时间复杂度也是 $O(\log n)$

精度证明

那么为什么DIGM算法，它的估算误差一定是小于50%的呢？

我们假设最后的桶的大小是 $2^r$ ，那么我们在加完前面的桶之后，最后要加上的size = $2^{r-1}$

如果这个桶没滑出去，刚好在窗口末尾停下了，那么我们就相当于少了了 $2^{r-1}$

如果这个桶基本全滑出去了，在窗口内可能只留了1个数字，那么我们就相当于多了$2^{r-1}$

但是，我们把之前的窗口全加起来： $1+2+4\cdots+2^{r-1} = 2^{r}-1$ ，他肯定是大于 等于$2^{r-1}$ 的，因此这个误差$2^{r-1}$ 肯定是小于50%的。

Extension

现在，给出一个可以进一步削弱误差的方法。

除了第一个和最后一个桶之外，其余的桶，可以将数量维持在：r-1 个或者 r 个, (r > 2)

这时候，这个算法的空间复杂度会变成 $O(r\log n)$ 但是误差率会从 50% 变成 $O(\frac{1}{r})$

此外，除了用来技术0.1，还可以用来维持一个平均值：

但是，这个算法只能进行一些简单的功能计算，要求桶内的值必须有可加性，因此推广性比较差

Counting Distinct Elements

给定一个数据流，我们来统计这个数据流中一共出现过多少不同的元素。

比如说，现在有一个集合，然后过来一个数据流，我们要统计多少这个集合的元素在这个数据流中出现了，多少没有出现。

还有其他应用场景：

  • 一个网页中出现了多少个不一样的词，词典是固定的，但词的分布是不一样的
  • 一周之内，用户总共访问了多少个不同的网站

一个很简单的方法就是：维护一个哈希表，然后过来一个数据我们映射一个数据，最后看哈希表中有哪些数据。但问题也是类似的，哈希表的大小事$O(n)$ 级别的，当数据流非常大的时候，这个哈希表是很难维护的。

因此，我们要考虑一种新的数据流算法

Flajolet-Martin Approach

FM 算法设计了一种空间复杂度为$O(\log_2(N))$ 的算法

在这个算法中，对于长度为N的数据流，我们将其映射到 长度为$\log_2(N)$ 的哈希表中。

举例来说，给定序列{e1, e2, e3, e2}，独立元素数目N = 3。这里哈希数组的长度为$\log_2(4) = 2$

假设给定哈希函数H(e)，有：

H(e1) = 00，TailZero(H(e1)) = 0

H(e2) = 01，TailZero(H(e2)) = 0

H(e3) = 10 ，TailZero(H(e3)) =1

第1步，将Max初始化为0；

第2步，对于序列中第1项e1，计算TailZero(H(e1)) = 0

第3步，对于序列中第2项e2，计算TailZero(H(e2)) = 0

第4步，对于序列中第3项e3，计算TailZero(H(e3)) = 1> Max, 更新Max；

第5步，对于序列中第4项e2，计算TailZero(H(e2)) =0

第6步，估计独立元素数目为 $\hat N = 2^{\max} = 2^1 = 2$。

在这个简单例子中，实际值 $N = 3$，估计值$ \hat N =2$

在实际应用中，为了减小误差，提高精度，我们通常采用一系列的哈希函数$H_1(e), H_2(e), H_3(e)$，计算一系列的Max值$\max_1,\max_2,\max_3$，从而估算一系列的估计值$2^{\max_1}, 2^{\max_2}, 2^{\max_3}$，最后进行综合得到最终的估计值。具体做法是：首先设计A*B个互不相同的哈希函数，分成A组，每组B个哈希函数；然后利用每组中的B个哈希函数计算出B个估计值;接着求出B个估计值的算术平均数为该组的估计值；最后选取各组的估计值的中位数作为最终的估计值。

举例来说，对于序列S，使用3*4 = 12个互不相同的哈希函数H(e)，分成3组，每组4个哈希函数，使用12个H(e)估算出12个估计值：

Computing Moments

首先给出Moments 的概念

假设数据流是由一些数字构成的，$m_i$ 代表元素i 在流中出现的次数，那么

$k^{th}$ Moment 就是：

刚才我们做的 FM 算法，就是$k^0$ moment

$k^0$ moment: 不同元素的数量

$k^1$ moment: 元素数量的计算，也就是数据流的长度N

$k^2$ moment = suprise number S : 衡量分布的不均匀程度

这里重点考虑 $k^2$ moment

比如说数据流A、B的长度为100，一共出现了11个不同的元素

数据流A各个元素的计数：10,9,9,9 ,9,9,9, 9,9,9,9 那么 $k^2 $ moment = 910

数据流B各个元素的计数：90,1,1,1,1,1,1,1,1,1,1 那么 $k^2 $ moment = 8110

AMS Method

AMS 方法可以对所有moment的值进行一个无偏估计，这里就只针对 $k^2$ moment

我们对于一个变量 $X$

  • 用 $X.{el}$
  • 用 $X.val$

Counting Itemsets

-------------本文结束，感谢您的阅读-------------