机器学习-感知机

破防了，还有4天就要期末考了，现在才开始做机器学习的第一份笔记

概要

其实感知机就是一个神经元。 它有如下几个特点

• 输入为实例的特征向量，输出为实例的类别，取+1和-1

• 感知机对应于输入空间中将实例划分为正负两类的分离超平面，属于判别模型

• 导入基于误分类的损失函数

• 利用梯度下降法对损失函数进行极小化

  • 感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式

接下来对感知机模型进行拆解：

第一个：输入部分

第二个：权重（就是w向量）；权重是在我们进行训练期间计算的值，初始呢我们是用一些初始值来可以进行随机的初始化，然后在学习过程当中对他们进行更新，最后我们模型学习完之后，这就是我们学习到的参数向量。我们用w来表示。

第三个：偏置项，这个偏置对应到上图在输入里边我们有一个常量1, 实际上这个常量1就相当于乘以1, 实际上就是, 后边的计算是和输入是无关的，相当于就是一个偏置，相当于i从1开始一直到n，还加上一个，这就是一个偏置。

由输入空间到输出空间的函数：

$$f(x) = sign(w\cdot x+b)$$

符号函数：

$$sign(x) = \begin{cases}+1&x\geq 0\\-1&x<0\end{cases}$$

几何解释

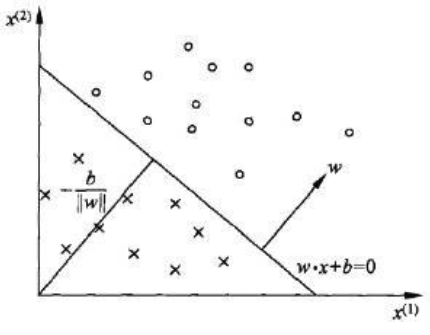
对于线性方程：

$$w\cdot x+b = 0$$

相当于在平面空间中的超平面S，w 是法向量，b是截距，用来分割开正负两种类别：

感知机学习策略

如何定义损失函数？

自然选择：误分类点的数目，但损失函数不是w,b连续可导，不宜优化。

另一选择：误分类点到超平面的总距离：

首先，距离函数：

$$d = \frac{|w\cdot x_0+b|}{||w||}$$

误分类点： $-y_i(w\cdot x_i+b)>0$

误分类点距离：

$$-\frac{1}{||w||}\sum_{x_i\in M} y_i(w\cdot x_i+b)\\ w' = \frac{w}{||w||} ,b' = \frac{b}{||w||}$$

损失函数：

$$L(w,b) = -\sum_{x_{i}\in M} y_i(w\cdot x_i+b)$$

为了优化损失函数：

$$\min_{w,b}L(w,b) = -\sum_{x_i\in M}y_i(w\cdot x_i+b)$$

我们使用梯度下降法来更新损失函数。

感知机学习算法

原始形式

输入：训练数据集 $T =\big{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N) \big}$, 期中 $x_i\in \mathcal X =R^n,y_i\in\mathcal y = {-1,+1}$ $i=1,2\cdots,N$ ， 学习率 $\eta(0<\eta\leq1)$

输出：w,b ： 感知机模型 $f(x) = sign(w\cdot x+b)$

1. 选取初值 $w_0,b_0$

2. 在训练集中选取数据$(x_i,y_i)$

3. 如果 $y_i(w\cdot x_i+b)\leq 0$, 说明分类错误:

   $$\begin{align} &w \leftarrow w+\eta ~y_ix_i\\ &b \leftarrow b+\eta y_i \end{align}$$

4. 转至2，直至训练集中没有误分类点

比如说 正样本点是. $x_1=(3,3)^T,x_2=(4.3)^T$. 负样本点是 $x_3=(1,1)^T$. 试用感知机学习算法原始形式求感知机模型.

1. 取初值 $w_0 = 0,b_0= 0,\eta = 1$

2. 对 $x_1 = (3,3)^T, y_1(w_0\cdot x_1+b_0)=0$ ，未能被正确分类，更新 $w,b$

$$\begin{align} &w_1 = w_0+y_1x_1 = (3,3)^T\\ &b_1=b_0+y_1 = 1 \end{align}$$

​ 得到新的线性模型： $w_1\cdot x+b_1 = 3x^{(1)}+3x^{(2)}+1$

1. 对于$x_1,x_2$显然模型大于0，被正确分类，对$x_3 = (1,1)^T$ 为负例 ，但计算得到$y_3(w_1\cdot x_3+b_1)<0$ 被误分类, 更新$w,b$ $$\begin{align} &w_2 = w_1+y_3x_3 = (2,2)^T\\ &b_2 = b_1+y_3 = 0 \end{align}$$

算法的收敛性：证明经过有限次迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型。

对偶形式

感知机算法的对偶形式的基本想法是：

将w和b表示为实例$x_i$和标记 $y_i$ 的线性组会的形式，通过求解其系数而求得$w$和$b$

由于

$$\begin{align} &w \leftarrow w+\eta ~y_ix_i\\ &b \leftarrow b+\eta y_i \end{align}$$

最后学习到的$w,b$为：

$$\begin{align} &w =\sum_{i=1}^N \alpha_i y_ix_i\\ &b =\sum_{i=1}^N \alpha_i y_i \end{align}$$

输入：训练数据集 $T =\big{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N) \big}$, 期中 $x_i\in \mathcal X =R^n,y_i\in\mathcal y = {-1,+1}$ $i=1,2\cdots,N$ ， 学习率 $\eta(0<\eta\leq1)$

输出：感知机模型 $f(x) = sign\bigg(\sum_{j=1}^N\alpha_jy_jx_j\cdot x+b\bigg)$
其中 $\alpha = (\alpha_1,\cdots,\alpha_N)^T$

1. $\alpha\leftarrow 0,b\leftarrow 0,\eta\leftarrow 1$

2. 在训练集中选取数据 $(x_i,y_i)$

3. 如果

   $$\begin{align} &y_i\bigg(\sum_{j=1}^N \alpha_jy_j(x_j\cdot x_i)+b \bigg)\leq 0\\ &\alpha_i\leftarrow \alpha_i+ \eta\\ &b\leftarrow b+\eta y_i \end{align}$$

4. 转至(2) 直到没有误分类数据

比如说 正样本点是. $x_1=(3,3)^T,x_2=(4,3)^T$. $y_1=y_2=1$ ; 负样本点是 $x_3=(1,1)^T, y_3 = -1$ .试用感知机学习算法对偶形式求感知机模型.

1. 首先$\alpha_i$ 都是0，因为每个都没有误分，因此$b=\alpha_i\cdot y_i = 0$ 所以这就是表2.2的第一列

2. 接着，就是进入迭代过程，首先计算第一个点

$$\begin{align} &y_i(\sum\alpha_j y_j x_j\cdot x_i+b)\\ &=1*((0*1*(3,3)^T\cdot(3,3)+0*1*(4,3)^T\cdot(3,3)+0*-1*(1,1)^T\cdot(3,3))+0)\\ &=0 \end{align}$$

那么就出现误分类，则此时，更新$\boldsymbol \alpha,b$ ,而这就是表2.2的第二列

$$\alpha_1 = 0,\alpha_2=0,\alpha_3 = 0\\ b = 0+1\cdot1 = 1$$

1. 接着进行判断，第二个点，发现没有误分类，进行判断第三个点

$$\begin{align} &y_i(\sum\alpha_j y_j x_j\cdot x_i+b)\\ &=-1*((1*1*(3,3)^T\cdot(1,1)+0*1*(4,3)^T\cdot(1,1)+0*-1*(1,1)^T\cdot(1,1))+1)\\ &=-1*(((3,3)^T\cdot(1,1))+1)\\ &=-(6+1)\\ &=-7<0 \end{align}$$

因此该点为误分类点，此时，更新$\boldsymbol \alpha,b$ ,而这就是表2.2的第三列

$$\alpha_1 = 1,\alpha_2=0,\alpha_3 = 1\\ b = 1+1\cdot-1 = 0$$

以此类推

k	0	1	2	3	4	5	6	7
		$x_1$	$x_3$	$x_3$	$x_3$	$x_1$	$x_3$	$x_3$
$\alpha_1$	0	1	1	1	1	2	2	2
$\alpha_2$	0	0	0	0	0	0	0	0
$\alpha_3$	0	0	1	2	3	3	4	5
b	0	1	0	-1	-2	-1	-2	3

习题

感知机因为是线性模型，所以不能表示复杂的函数，如异或(XOR) 。验证感知机为什么不能表示异或。

直观上，我们设正方形为True, 三角形为False

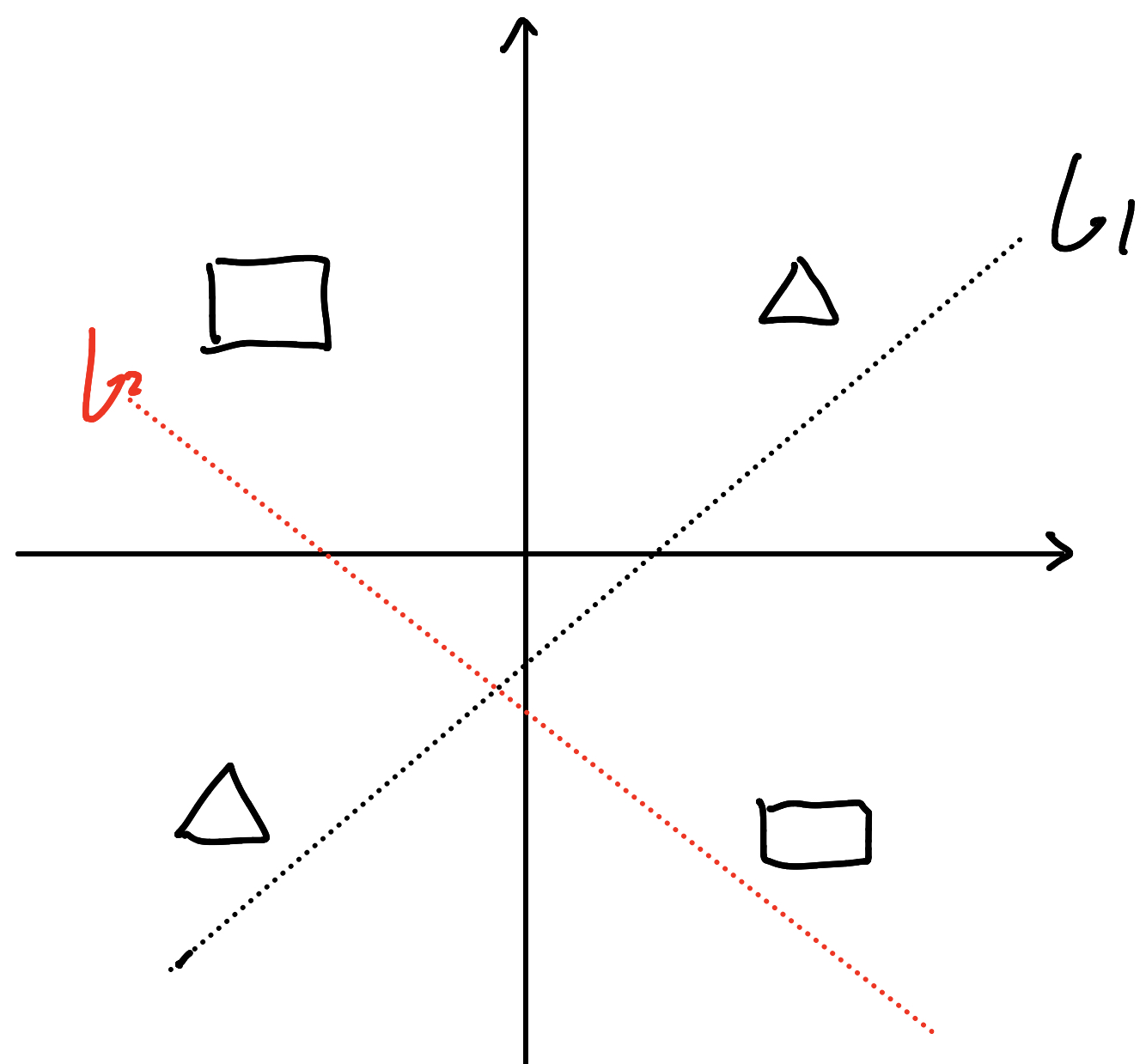
那么，我们是没有办法找到一条直线将其分离的，如上图

在数学形式上：

$$\text{设}~~sign(x) = \begin{cases}1&x\geq 0\\-1&x<0 \end{cases}$$

我们令 $f(x) = sign(w\cdot x+b)$ $w$为权重$(w_1,w_2)$ ，b为偏置

设向量$\boldsymbol x = (x_1,x_2)$ ，用其表示异或问题

• 若 $x_1=x_2=0,f(x)=-1$ 则有 $b<0$
• 若 $x_1=0,x_2=1,f(x)=1$ 则有 $w_1\cdot 0+w_2\cdot1 +b >0$ . 因此 $w_2>-b>0$
• 若 $x_1=01,x_2=0,f(x)=1$ 则有 $w_1\cdot 1+w_2\cdot0 +b >0$ . 因此 $w_1>-b>0$
• 若 $x_1=x_2=1,f(x)=-1$ ，当前由上面三个式子，有 $w_2>-b>0,w_1>-b>0$ , 所以应该是 $w_1+w_2-(-b)>0$ 。 但是这和 $f(x)=-1$ 矛盾