机器学习-朴素贝叶斯

概要

1. 朴素贝叶斯法是典型的生成学习方法生成方法由训练数据学习联合概率分布$P(X,Y)$ 然后求得后验概率分布$P(Y |X)$. 具体来说, 利用训练数据学习 $P(X|Y)$ 和 $P(Y)$ 的估计，得到联合概率分布:

$$P(X,Y)= P(Y)P(X|Y)$$

概率估计方法可以是极大似然估计 或者是 贝叶斯估计

1. 朴素贝叶斯法的基本假设是条件独立性

$$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_k)\\ =\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)$$

这是一个较强的假设.由于这一假设，模型包含的条件概率的数量大为减少，朴素贝叶斯法的学习与预测大为简化.因而朴素贝叶斯法高效，且易于实现.其缺点是分类的性能不一定很高.

1. 朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测

$$P(Y|X) = \frac{P(X,Y)}{P(X)} = \frac{P(Y)P(X|Y)}{\sum_YP(Y)P(X|Y)}$$

将输入x 分到后验概率最大的类y

$$y = \arg\max_{c_{k}} P(Y=c_k)\prod_{j=1}^nP(X_j=x^{(j)}|Y=c_k)$$

后验概率等价于0-1损失函数时的期望风险最小化.

朴素贝叶斯学习与分类

基本方法

训练过程

对于训练数据集：输入为特征向量 $x\in\mathcal X\subseteq \boldsymbol R^n$ ，输出位类标记 $y\in \mathcal Y ={c_1,c_2\cdots,c_k}$

$$T = \{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N) \}$$

由 $P(X,Y)$ 独立同分布产生。

然后，朴素贝叶斯法 会通过训练数据集学习联合概率分布 $P(X,Y)$ ，也就是学习先验概率分布以及条件概率分布

• 先验概率分布：

  $$P(Y=c_k),k=1,2\cdots,K$$

• 条件概率分布

  $$P(X=x|Y=c_k) = P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_k),k=1,2\cdots,K$$

于是，学习到联合概率分布 $P(X,Y)$

条件概率分布 $P(X=x|Y=c_k)$ 有着指数级数量的参数，其估计实际是不可行的。因此，朴素贝叶斯法对条件概率分布做了条件独立性假设。具体的，条件独立性假设是：

$$P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_k)\\ =\prod_{j=1}^n P(X^{(j)}=x^{(j)}|Y=c_k)$$

条件独立假设等于是说：用于分类的特征在类确定的条件下都是条件独立的。这一假设使得朴素贝叶斯法变得简单，但有时会牺牲一定的分类准确率。

分类过程

朴素贝叶斯法分类时，对给定的输入x，通过学习到的模型计算后验概率分布 $P(Y=c_k|X=x)$ ，将后验概率最大的类作为$x$ 的输出。后验概率计算根据贝叶斯定理进行：

$$P(Y=c_k|X=x) = \frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_k P(X=x|Y=c_k)P(Y=c_k)}$$

将独立性假设带入上式，可得：

$$P(Y=c_k|X=x) = \frac{P(Y=c_k)\prod_{j=1}^n P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(X=x|Y=c_k)\prod_{j=1}^n P(X^{(j)}=x^{(j)}|Y=c_k)} ,~~~k=1,2,\cdots,K$$

这是朴素贝叶斯法分类的基本公式。于是，朴素贝叶斯分类器科表示为：

$$y = f(x) = \arg\max_{c_k}\frac{P(Y=c_k)\prod_{j=1}^n P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(Y=c_k)\prod_{j=1}^n P(X^{(j)}=x^{(j)}|Y=c_k)}$$

注意到，在上式中，分母对所有 $c_k$ 都是相同的，因此直接拿掉了

$$y = \arg\max_{c_{k}} P(Y=c_k)\prod_{j=1}^nP(X_j=x^{(j)}|Y=c_k)$$

朴素贝叶斯的学习与分类算法

朴素贝叶斯算法

输入：训练数据 $T = {(x1,y_1),(x_2,y_2),\cdots,(x_N,y_N) }$ ，其中 $x_i = (x_i^{(1)},\cdots,x_i^{(n)})^T$. $x_i^{(j)}$ 是第i个样本的第j 个特征，$x_i^{(j)}\in{a{j1},\cdots,a{jS_j} }$ , $a{jl}$ 是第j个特征可能取的第 l 个值。

$$j=1,2\cdots,n\\ l=1,2\cdots,S_j\\ y_i\in \{c_1,c_2,\cdots,c_k\}$$

以及测试数据 ：实例x

输入：实例x的分类

1. 计算先验概率及条件概率

$$P(Y=c_k) = \frac{\sum_{i=1}^NI(y_i=c_k)}{N},k=1,2\cdots,K\\~\\$$

第一步是计算输入 $c_k$ 的训练数据占所有训练数据的比值

$$P(X^{(j)}=a_{jl}|Y=c_k)=\frac{\sum_{i=1}^N I(x_i^{(j)}=a_{jl},y=c_k)}{\sum_{i=1}^N I(y_i=c_k)}\\~\\ j=1,2\cdots,n;~l=1,2\cdots,S_j;~y_i\in \{c_1,c_2,\cdots,c_k\}$$

第二步是计算条件概率

1. 对于给定的实例 $x=(x^{(1)},\cdots,x^{(n)})^T$ 计算：

$$P(Y=c_k) \prod_{j=1}^n P(X^{(j)}=x^{(j)}|Y=c_k) ,k=1,2\cdots,K$$

1. 确定实例 $x$ 的类

$$y = \arg\max_{c_k}P(Y=c_k)\prod_{j=1}^n P(X^{(j)}=x^{(j)}|Y=c_k)$$

例子

试由下表的训练数据学习一个朴素贝叶斯分类器并确定$x=(2,S)^T$的类标记 y. 表中$X^{(1)}, X^{(2)}$ 为特征，取值的集合分别为，$A_1={1 , 2, 3} , A_2={S, M,L}$ ; $Y$ 为类标记， $Y\in C = {1 , -1}$

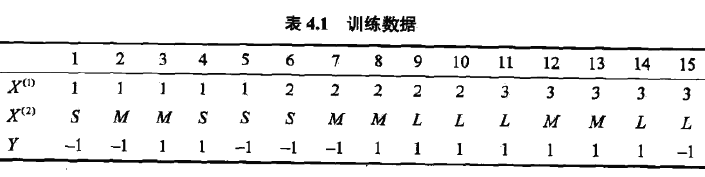
1. 计算先验概率，首先统计正例和负例的个数。

这里，正例有9个，负例有6个。因此:

$$P(Y=1) = 9/15\\ P(Y=-1) = 6/15$$

1. 计算条件概率，一共要计算 $2\times(3+3)=12$个概率

$$\begin{align} &P(X^{(1)}=1|Y=1)=\frac{2}{9},P(X^{(1)}=2|Y=1)=\frac{3}{9},P(X^{(1)}=3|Y=1)=\frac{4}{9}\\ &P(X^{(2)}=S|Y=1)=\frac{1}{9},P(X^{(2)}=M|Y=1)=\frac{4}{9},P(X^{(2)}=L|Y=1)=\frac{4}{9}\\ &P(X^{(1)}=1|Y=-1)=\frac{3}{6},P(X^{(1)}=2|Y=-1)=\frac{2}{6},P(X^{(1)}=3|Y=-1)=\frac{1}{6}\\ &P(X^{(2)}=S|Y=-1)=\frac{3}{6},P(X^{(2)}=M|Y=-1)=\frac{2}{6},P(X^{(2)}=L|Y=-1)=\frac{1}{6}\\ \end{align}$$

1. 计算后验概率，对给定的测试样本 $x=(2,S)^T$ 进行计算

$$\begin{align} &P(Y=1)P(X^{(1)}=2|Y=1)P(X^{(2)}=S|Y=1) =\frac{9}{15}\frac{3}{9}\frac{1}{9} = \frac{1}{45}\\ &P(Y=-1)P(X^{(1)}=2|Y=-1)P(X^{(2)}=S|Y=-1)=\frac{6}{15}\frac{2}{6}\frac{3}{6} = \frac{1}{15} \end{align}$$

由于$P(Y=-1)P(X^{(1)}=2|Y=-11)P(X^{(2)}=S|Y=-1)$ 是两种情况中最大的，因此 最终的预测结果是 $y=-1$

贝叶斯估计

用极大似然估计可能会出现所要估计的概率值为0 的情况. 这时会影响到后验概率的计算结果(只要一个概率值为0就都为0)，使分类产生偏差解决这一问题的方法是采用贝叶斯估计

具体地

先验概率的贝叶斯估计是

$$P_\lambda (Y=c_k) = \frac{\sum_{i=1}^NI(y_i=c_k)+\lambda}{N+K\lambda}$$

条件概率的贝叶斯估计是

$$\begin{align} &P_\lambda (X^{(j)}=a_{jl}|Y=c_{k}) = \frac{\sum_{i=1}^N I(x_i^{(j)}=a_{jl},y=c_k)+\lambda}{\sum_{i=1}^N I(y_i=c_k)+S_j\lambda }\\~\\ &j=1,2\cdots,n;~l=1,2\cdots,S_j;~y_i\in \{c_1,c_2,\cdots,c_k\} \end{align}$$

式中 $\lambda \geq 0$, 等价于在随机变量各个取值的频数上赋予一个整数 $\lambda >0$ . 当 $\lambda=0$ 时，就是极大似然估计。常常取 $\lambda = 1$ ,这称为拉普拉斯平滑 。

显然，对任何 $l=1,2\cdots,S_j,k=1,2\cdots,K$ ,有条件概率大于0

$$\begin{align} &P_\lambda (X^{j} = a_{jl}|Y=c_k) > 0\\~\\ &\sum_{l=1}^{S_j}P(X^{(j)}=a_{jl}|Y=c_k)=1\\ \end{align}$$

例子

试由下表的训练数据学习一个朴素贝叶斯分类器并确定$x=(2,S)^T$ 的类标记 $y$ 。 表中$X^{(1)}, X^{(2)}$ 为特征，取值的集合分别为，$A_1={1 , 2, 3} , A_2={S, M,L}$ $Y$ 为类标记， $Y\in C = {1 , -1}$

按照拉普拉斯平滑估计概率 ，即取 $\lambda = 1$

1. 先验概率的贝叶斯估计

$$P(Y=1) = \frac{9+1}{15+2\times1} = \frac{10}{17}\\ P(Y=-1) = \frac{6+1}{15+2\times 1} =\frac{7}{17}\\$$

1. 计算条件概率

$$\begin{align} &P(X^{(1)}=1|Y=1)=\frac{2+1}{9+3*1}= \frac{3}{12},P(X^{(1)}=2|Y=1)=\frac{4}{12},P(X^{(1)}=3|Y=1)=\frac{5}{12}\\~\\ &P(X^{(2)}=S|Y=1)=\frac{2}{12},P(X^{(2)}=M|Y=1)=\frac{5}{12},P(X^{(2)}=L|Y=1)=\frac{5}{12}\\~\\ &P(X^{(1)}=1|Y=-1)=\frac{4}{9},P(X^{(1)}=2|Y=-1)=\frac{3}{9},P(X^{(1)}=3|Y=-1)=\frac{2}{9}\\~\\ &P(X^{(2)}=S|Y=-1)=\frac{4}{9},P(X^{(2)}=M|Y=-1)=\frac{3}{9},P(X^{(2)}=L|Y=-1)=\frac{2}{9}\\ \end{align}$$

由此我们可以看出，及时当前的条件样本数为0，条件概率也不会为0，而是 $p = \frac{\lambda}{\sum_{i=1}^N I(y_i=c_k)+S_j\lambda}$

1. 因此，对于给定的 $x=(2,S)^T$ ，我们计算后验概率

$$\begin{align} &P(Y=1)P(X^{(1)}=2|Y=1)P(X^{(2)}=S|Y=1) =\frac{10}{17}\frac{4}{12}\frac{2}{12} = \frac{5}{153}=0.0327\\ &P(Y=-1)P(X^{(1)}=2|Y=-1)P(X^{(2)}=S|Y=-1)=\frac{7}{17}\frac{3}{9}\frac{4}{9} = \frac{28}{459}=0.0610 \end{align}$$

由于$P(Y=-1)P(X^{(1)}=2|Y=-11)P(X^{(2)}=S|Y=-1)$ 是两种情况中最大的，因此 最终的预测结果是 $y=-1$