机器学习-支持向量机
学习支持向量机的时候,我们要一步一步来,从线性可分到线性不可分,一共有三种支持向量机。
- 线性可分支持向量机和线性支持向量机:输入空间和特征空间的元素一一对应,并将输入空间中的输入映射为特征空间中特特征向量
- 非线性支持向量机:利用一个从输入控件到特征空间的非线性映射将输入映射为特征向量
支持向量机的学习是在特征空间进行的
概要
线性可分支持向量机
支持向量机最简单的情况是线性可分支持向量机,或硬间隔支持向量机 , 构建它的条件是训练数据线性可分。其学习策略是最大间隔法, 可以表示为凸二次规划问题,其原始最优化问题为
求得最优化问题的解为 $w^,b^$ ,得到线性可分支持向量机,分离超平面是:
分类决策函数是
线性支持向量机(软间隔支持向量机 )
线性可分支持向量机
现在摆在我们面前的仍然是一个二分类问题。
- 训练数据集:
假设特征空间上的数据集
输入为特征向量 $x\in\mathcal X\subseteq \boldsymbol R^n$ ,$y_i\in\mathcal Y = {+1,-1},i=1,2\cdots,N$, $x_i$ 为第i个特征向量,也称为实例。$y_i$ 为 $x_i$ 的类标记,当$y_i=+1$ 时,称x为正例;当 $ y =-1 $时,称$x_i$为负例$(x_i,y_i)$称为样本点。 再假设训练数据集是线性可分的
学习目标: 找到分离超平面 $w\cdot x+b=0$ 。分离超平面将特征空间划分为两部分, 一部分是正类,一部分是负类。法向量指向的一侧为正类,另一侧为负类
学习策略:间隔最大化。
如下图,感知机可能会得到多个不同(w,b)的超平面,但是svm最终只会选择间隔最大的超平面
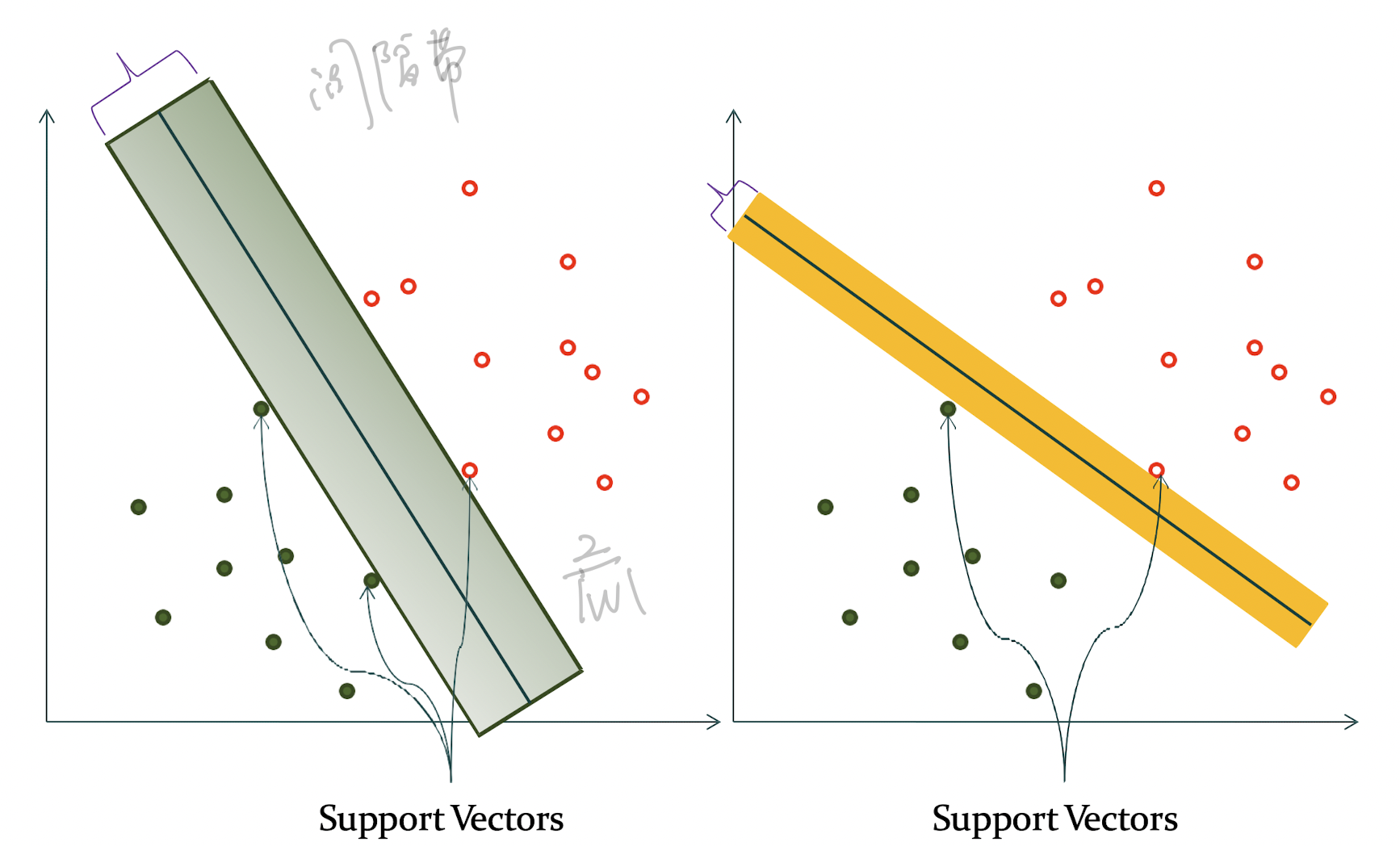
注意:
感知机利用误分类最小的策略,求得分离超平面。但是这个解是由无穷多个的,只要分对了就好
但是线性可分支持向量机利用间隔最大化来求最优分离超平面,这时候解就变成唯一的了
- 决策函数:
间隔
既然支持向量机要求间隔最大化,那么,间隔如何定义呢?
函数间隔
首先,我们要定义函数间隔.
对于给定的训练数据集T和超平面$(w,b)$,定义超平面关于样本点 $(x_i,y_i)$ 的函数间隔为:
然后,我们定义超平面(w,b)关于训练数据集T的函数间隔为 : 超平面$(w,b)$ 关于T中所有样本点$(x_i,y_i)$ 的函数间隔中的最小值。也就是
这相当于”感性“认识间隔,因为当成比例得改变w和b的话,超平面并没有改变,但是函数间隔却变成了原来的两倍。因此我们还需要给出几何间隔的定义
集合间隔
对于给定的训练数据集 T 和超平面$(w,b)$ ,定义超平面 $(w,b)$ 关于样本点$(x_i,y_i)$的几何间隔为:
然后,我们定义超平面(w,b)关于训练数据集T的几何间隔为 : 超平面$(w,b)$ 关于T中所有样本点$(x_i,y_i)$ 的几何间隔中的最小值。也就是
函数间隔和几何间隔有如下关系:
如果 $||w||=1$ ,那么函数间隔和几何间隔相等。
间隔最大化
学完了间隔,我们就要学习,怎么让间隔最大化(在线性可分中又叫硬间隔最大化)
一个感性又直观的解释是:对训练数据集找到几何间隔最大的超平面,意味着以充分大的确信度对训练数据进行分类。也就是说,我们不仅要将正负实例点分开,而且对最难分的实例点(距离超平面最近的点)也有足够大的确信度将它们分开。这样的超平面应该对未知的新实例有很好的分类预测能力。
因此我们可以这样来写一个约束最优化问题:
用通俗的话来说,我们希望最大化超平面关于训练数据集的几何间隔 $\mathcal Y$ 。约束条件表示的是,超平面关于每个训练样本点的几何间隔至少是$\mathcal Y$
上面这个式子比较麻烦,我们运用几何间隔和函数间隔 的关系,可以将上式改写为:
然后, 我们还是不满意,还是觉得有点复杂。因此我们可以将$\hat {\mathcal Y}=1$ ,函数间隔的这一改变对优化问题的不等式没有影响。而且我们也不喜欢分数,因为最大化 $\frac{1}{||w||}$ 和最小化 $\frac{1}{2}||w||^2$ 是等价的,因此可以得到最终版本的优化问题:
算法—最大间隔法
- 输入: 线性可分训练数据集 $T = {(x_1,y_1),\cdots,(x_N,y_N) }$ ,其中,$x_i\in \mathcal X = \boldsymbol R^n,y_i\in\mathcal Y = {-1,+1},i=1,2\cdots,N$
- 输出: 最大间隔分离超平面和决策函数
- 构造并求解 约束最优化问题:
求得最优解$w^,b^ $
- 得到分离超平面
分类决策函数:
支持向量和间隔边界
在线性可分的情况下,训练数据集的样本点中与分离超平面距离最近的样本点的实例,我们称其为支持向量,支持向量是使得约束条件式等号成立的点,即:
对于 $y_i = +1$ 的正例点,支持向量在超平面 $w\cdot x+b=1$上
对于 $y_i = -1$ 的正例点,支持向量在超平面 $w\cdot x+b= -1$上
如下图,$H_1,H_2$ 上的点,就是支持向量
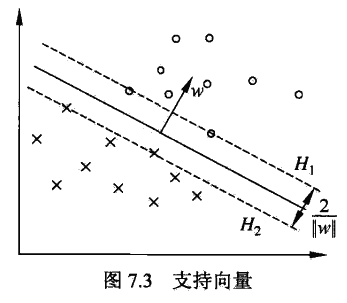
注意到 $H_1$和$H_2$ 平行,它们中间形成一条没有点的长带。长带的宽度等于 $\frac{2}{||w||}$,称$H_1$和$H_2$ 为间隔边界
例题

第一步:列出优化问题。 这里有x是二维的,因此我们 $\boldsymbol w = (w_1,w_2)$
带入正例点和负例点,可得:
第二步: 线性规划
我们要做的是尽量消去 b,然后再一个二维平面上做线性优化:
我们对上面式子做线性规划,可得:
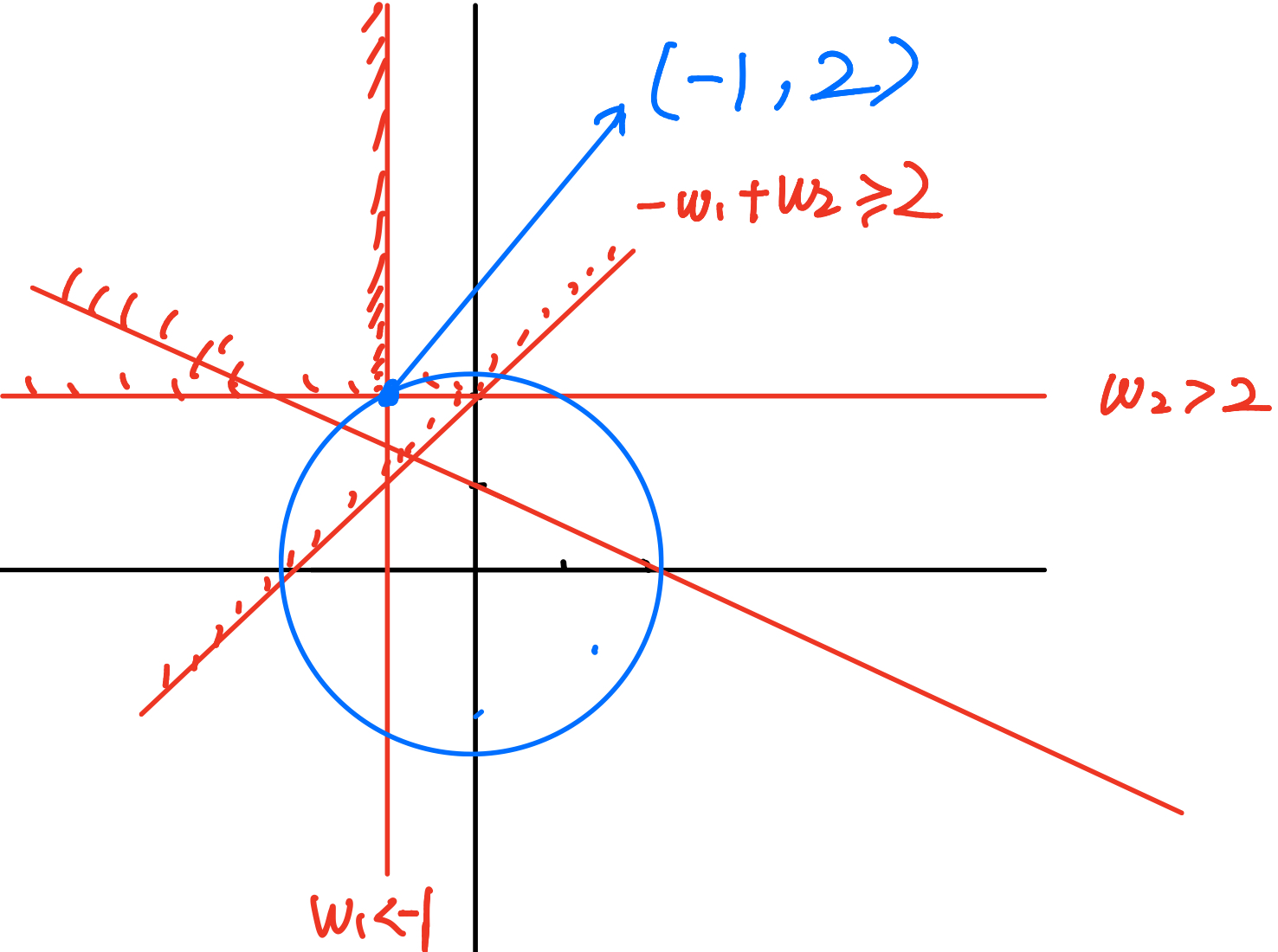
将 $(w_1,w_2)=(-1,2)$ 带入原方程,可得 $b=-2$
第三步:画出分离超平面,得到支持向量
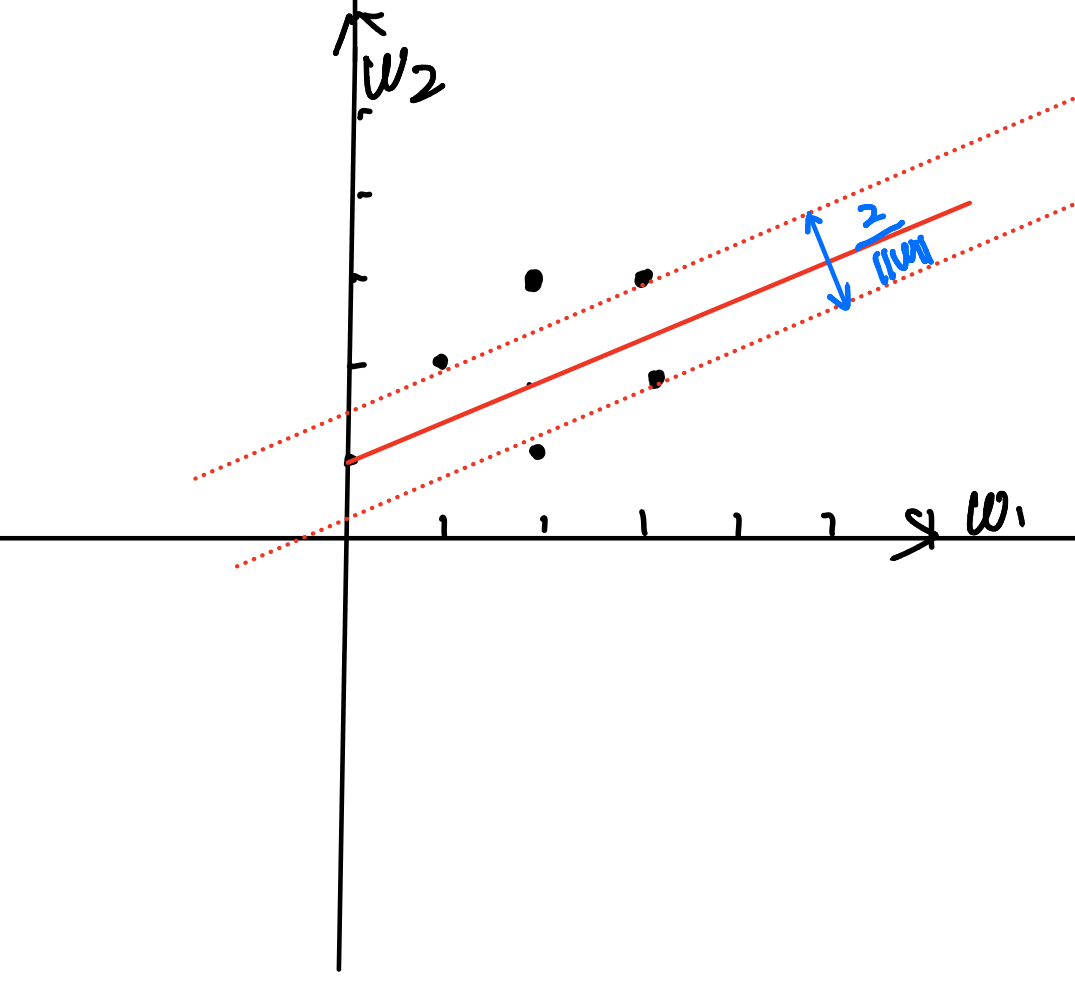
最终得到分离超平面为:
分类决策函数为
支持向量为:$(3,2),(1,2),(3,3)$
#