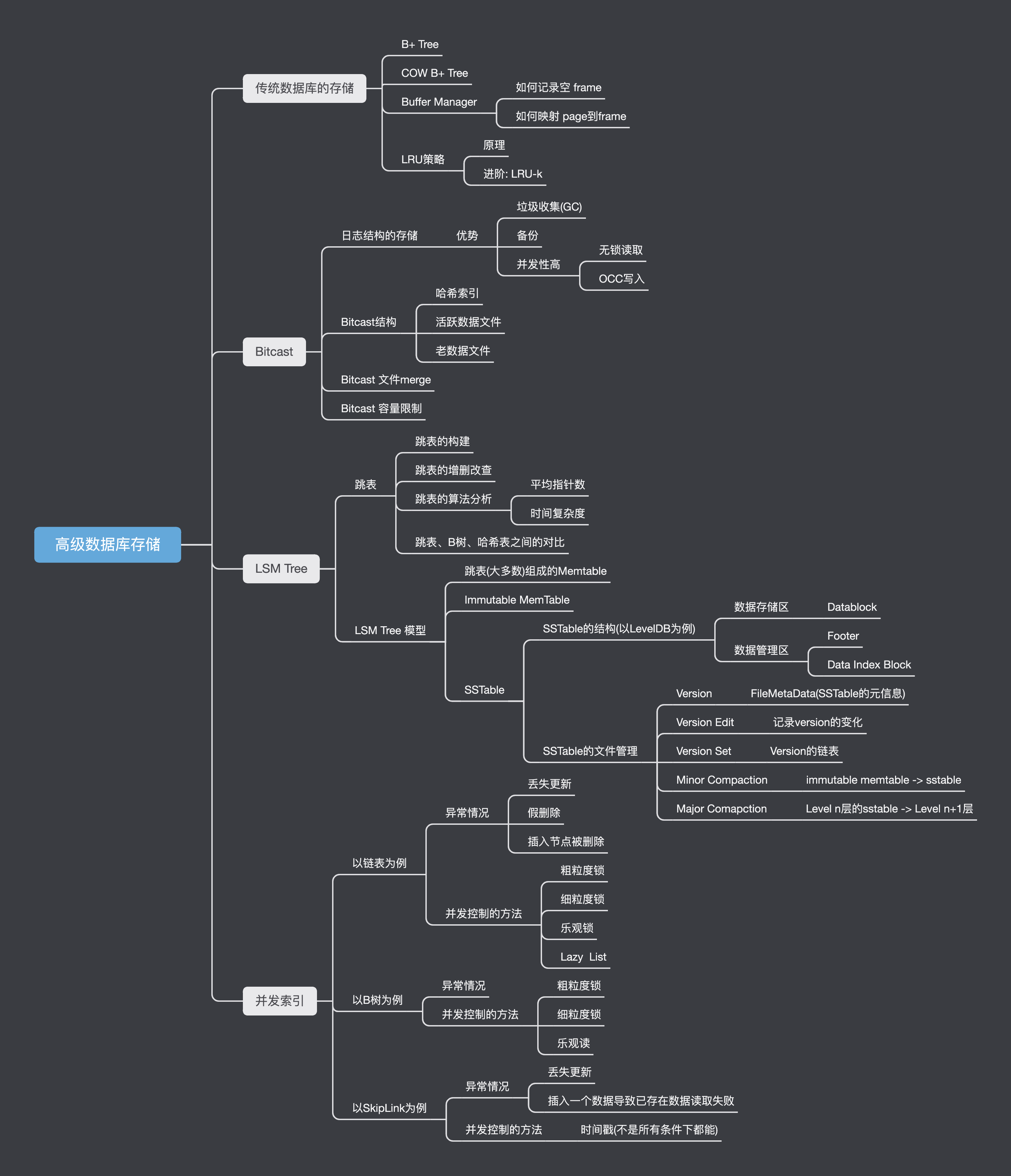
高级数据库-存储

参考博客：https://blog.csdn.net/helloworld_ptt/article/details/105801262

衡量或者评价一个数据库的性能，通常我们会从四个方面来进行：计算、事务、存储、高可用。现在，我们主要来学习数据库架构中存储这一块的知识。

传统数据库的存储

KVS接口与设计需求

KVS(Key Value System) 可以被认为属关系型数据库的基础。如果可以实现KVS，那么其中的Key就相当于关系型数据表中的主键，而Value则相当于数据表中的非主键列。最后，在KVS基础上封装一层Schema，就可以实现关系数据库的基本功能了。

那么在设计KVS的时候，我们需要 考虑哪几方面的内容？

• 需求
• 功能接口

这两点是最重要的，决定了整个项目的成败

• 架构
• 模块
• 模块内数据结构、算法
• 模块间接口
• 测试

上面几方面都和数据库性能有关

功能需求

那么，在KVS中，我们需要实现什么需求？

• 点操作，也就是 Put和Get操作，即通过put把数据存储到该系统中，再通过get从系统中取出数据
• 范围操作，即一次需要操作多个数据，比如说用get读取一片连续的数据。因此key的需要存储在连续的空间当中。
• 容错，因为可能会出现程序错误、宕机，因此在这种情况下，我们需要对已经写入的数据，能确保其不会丢失
• 一致性，即指事务执行的结果必须是使数据库从一个一致性状态变到另一个一致性状态，在单机状态下实现难度比较小。

基本接口

最终来说，我们需要KVS支持：

单点读和写

• db->Get(leveldb::ReadOptions(),key1,&value);
• if(s.ok())s=db->Put(leveldb::WriteOptions(),key2.value)
• if(s.ok())s=db->Delete(leveldb::WriteOptions(),key1s)

对范围的支持，我们可以用迭代器来实现：

leveldb::Iterator* it = db->Newlterator(leveldb::ReadOptions));
for (it-> Seek(start);
  it-> Valid( && it->key0.ToString0 < limit;
  it->Next) {...}

B+ Tree

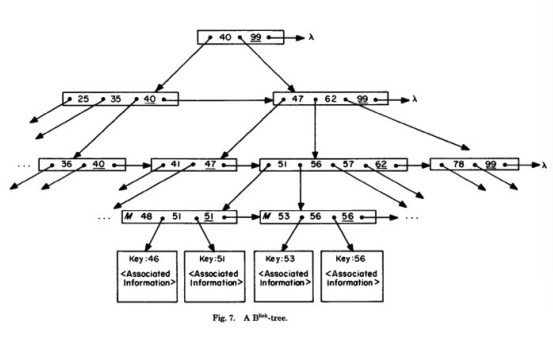
我们学过很多树形的数据结构，但是可能只有B+树可以满足KVS的需求。在 这篇博客 中，我们学习了B+树的增删改查。

那么为什么B+树可以满足KVS的设计呢？这就要联系到计算机体系结构的相关知识了。

我们知道计算机的存储都是以块为单位的，最底层的块设备(ssd或者磁盘)的块大小是4KB(不同存储介质不同)。因此，在这种情况下使用二叉树，是不可能使得一个节点充满整一个块的。

我们现在来看B+树的结构：

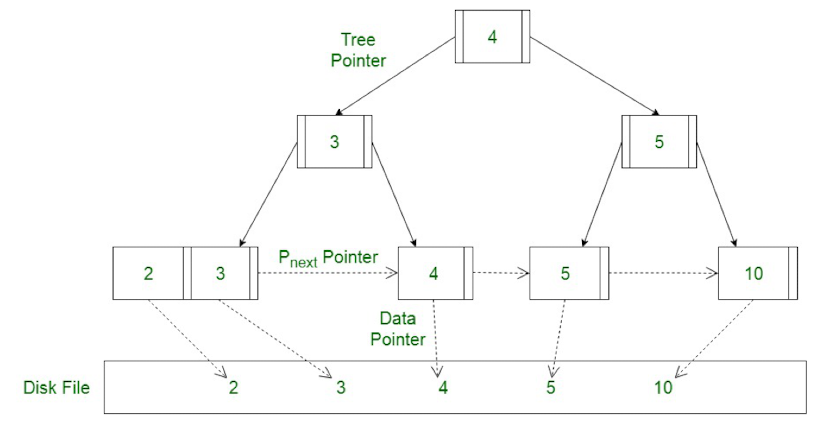
现在可以发现B+树的优点了

• B+树的一个节点可以容纳多个数据，而且可以和底层的块一一对应
• B+树和红黑树不一样，它是平衡的。这意味访问任何一个页所需要的深度是相等的，这样使得整体访问代价比较均衡。而且通常来说，一个三层的B+树就可以存储很多数据了，因此一颗B+树的并不会很高
• B+树支持范围查询，因为倒数第二层节点之间存在指针(严格意义上B+树并不是树)

append-only btree

但是如果我们要做内存中的存储，那么B+树就会显得性能不够，因此我们来学习一种改进后的数据结构： COW(copy on write) B+ Tree

考虑这个 3-level 的b+ 树。有两级分支页面（根为分支页面）和5个叶子节点。数据存储在叶子节点中。

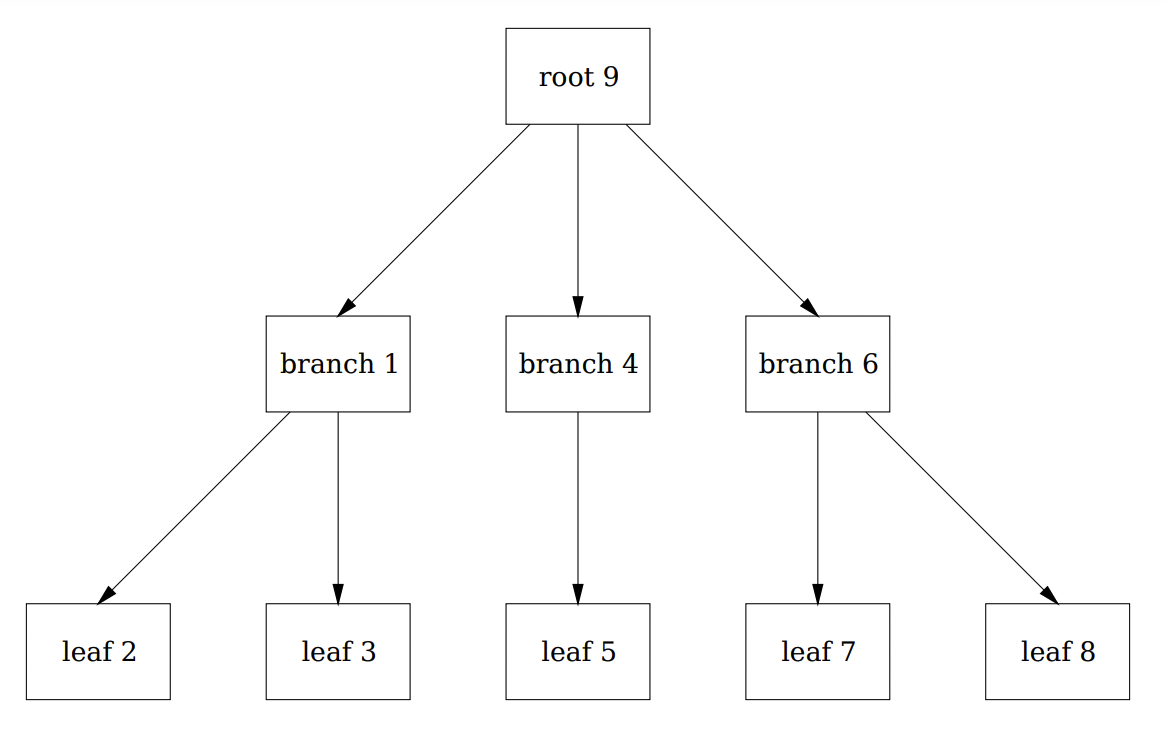
这个数据结构不支持叶子与叶子之间的指针(B+树支持) 以便于顺序访问，因为它需要在每次更新时重写整个树。

我们看到，实际上，这些节点是按照顺序存储在数据库文件中的，meta10节点包括指向根页面的指针，SHA1和统计计数器，当文件打开时，它被逐页向后扫描以找到有效的元页面，从而找到树的根。如下所示：

在COW B+ Tree中，叶子(数据块)是存放在连续空间上的，当我对某一个块进行修改的时候，并不是就地修改页面，而是新建一个页面。并更改索引。如下所示：

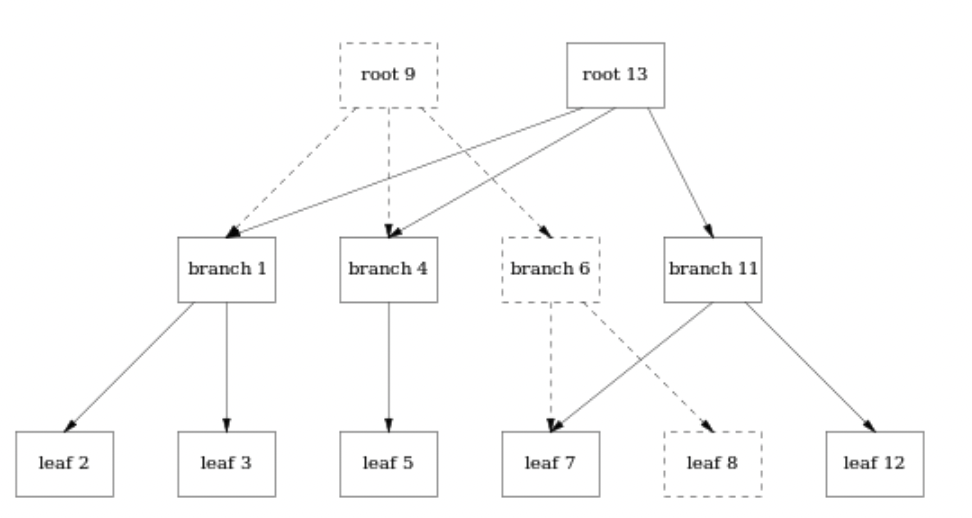
当我更新了 leaf 8 中的值，不是就地更改页面，而是生成一个 leaf12。

因为页面的位置发生了变化，所以每个父页面都需要更新以指向新的位置：

• branch6是 leaf7和leaf8的父页面，因此需要生成一个新的branch11指向leaf7(保持不变)和新生成的页面leaf12
• root9是树根，自然需要发生变化，因此需要生成一个root13，指针指向branch1.branch4和branch11。需要注意，root9并不是被删除了，图表中的虚线和指针仍然存在与文件中，只是并不是当前版本罢了。

因此，使用这种数据结构，通过将新页面附加到原有文件之后来写入页面。使得已经写入的页面永远都不会被修改。

将树写成顺序形状，如下所示：

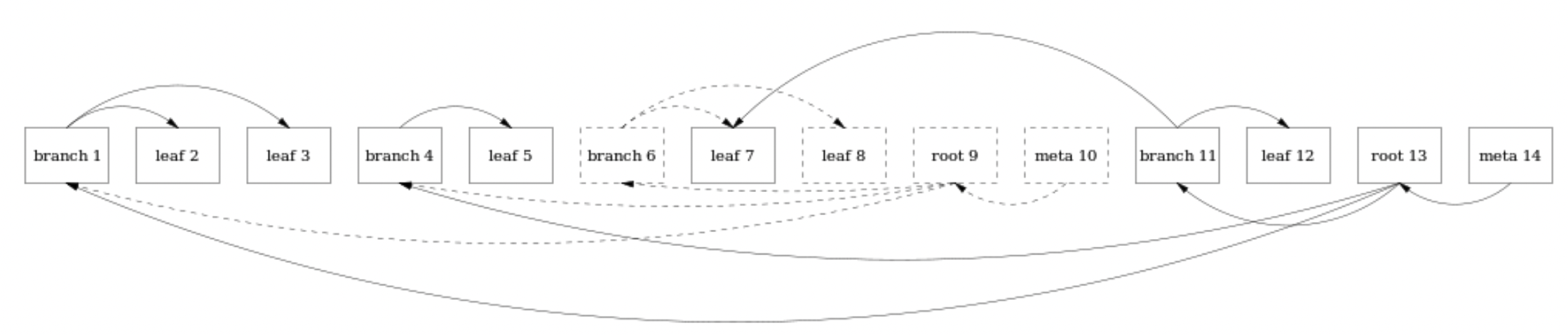
那么有人就要问了：每一次都要生成一个新版本的树，不是很浪费空间吗？但事实上，这是一种以空间换时间的方法，将连续页面写入磁盘比随机写入位置更加有效，而且不需要记录事务日志，因为数据库文件就是事务日志。

但是我们要知道，无论使用B+树还是COW B+树，都会导致写放大。因为在写入的时候，除了更新页数据之外，还要更新元数据。因此实际写入的物理数据量是写入数据量的多倍。

Database Buffer

我们知道，如果所有数据都存放在磁盘，每次数据库访问的时候都需要到磁盘里读取，那么，数据访问就讲受限于磁盘的IO，严重影响访问性能。因此，就引入了缓冲区架构：

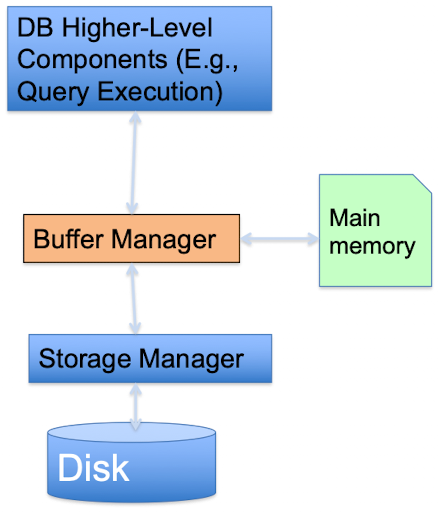
缓冲区相当于在数据库和磁盘中间的一层，由缓存管理器管理，它将决定那些Page需要放到缓冲区。这样一来，任何数据库的请求都需要经过缓冲区才能实现。

缓冲区内部结构可以具象为下图：我们把缓冲区中的每一格称为一个Frame，每个Frame可以放一个Page

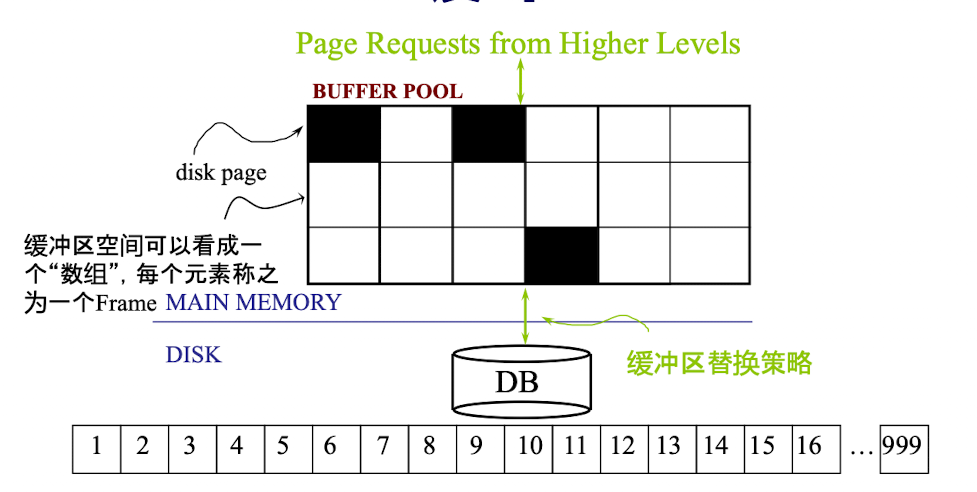
问题是，我们要设计一个高效的缓冲区的话，从管理上必须考虑这几个问题：

• 怎么知道哪些Frame是空的？
  • 扫描
  • 维护一个空的Frame列表
  • 使用一个Bitmap

• 知道Dist page存放在哪个Frame当中

  • 使用哈希表，将 page id 映射到frame id

• 如果缓冲区已经满了，该怎么办？

  • 在CSAPP中，我们学习过LRU策略，就是淘汰最近没有使用的页，其实还有很多替换策略

Implement LRU-Cache

上面我们说LRU策略是比较常用的淘汰机制。那么LRU有哪些缺点呢？

1. LRU对循环读取的场景不太友好，比如我们循环读取第1、2、3、4页，那么我们刚把1淘汰掉，就需要去读取第1页了。
2. LRU会引入很冷的数据。比如某一页只出现了一次，也会出现在缓冲区当中，并在相当一段时间里面占有一个位置。

因此，我们可以对LRU做一个优化——LRU-K

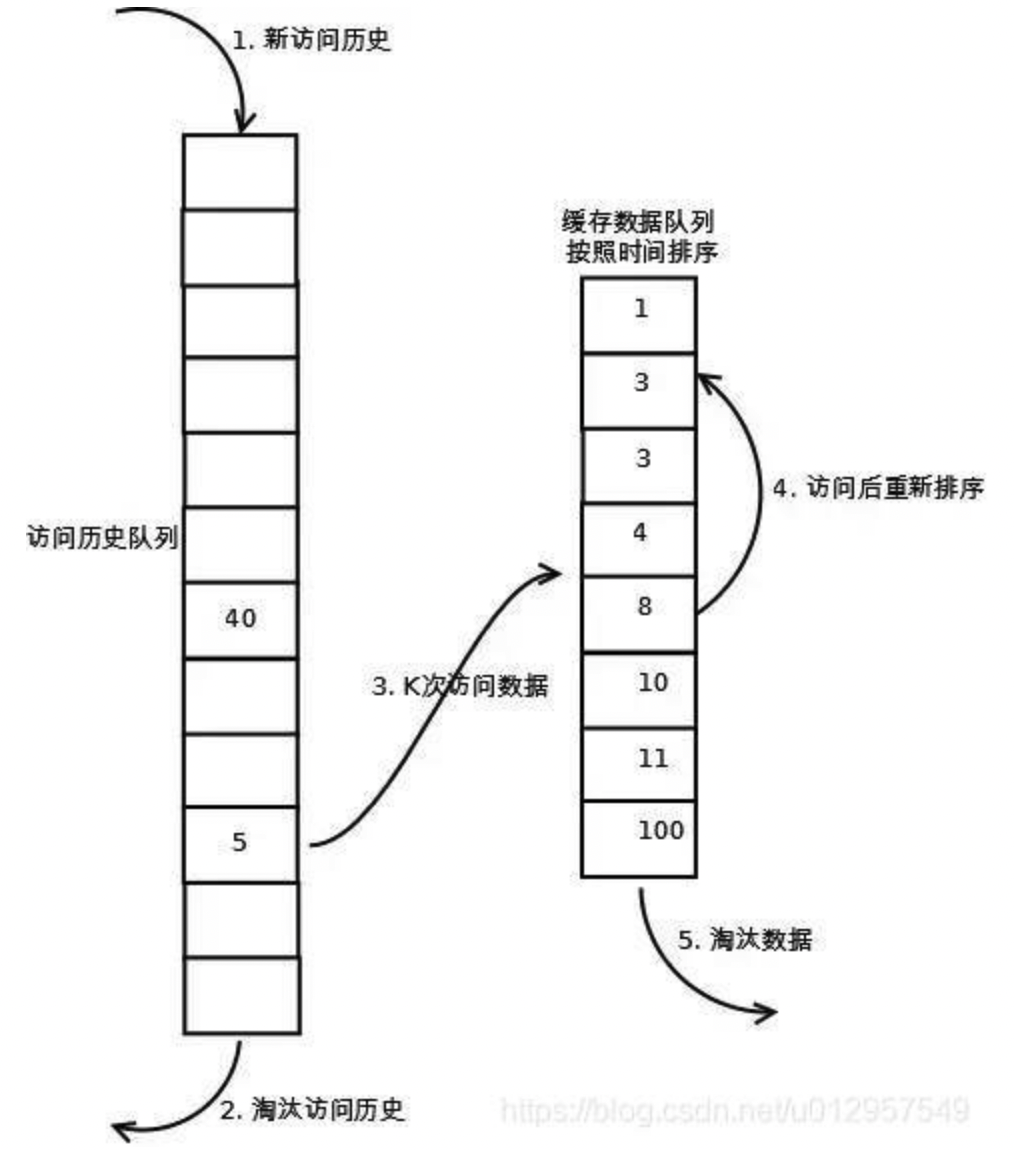
LRU-K需要多维护一个队列或者更多，用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候，才将数据放入缓存。当需要淘汰数据时，LRU-K会淘汰第K次访问时间距当前时间最大的数据。

• 第一步添加数据照样放入第一个队列的头部
  • 如果数据在该队列里访问没有达到K次（该数值根据具体系统qps来定）则会继续到达链表底部直至淘汰；
  • 如果该数据在队列中时访问次数达到了K次，那么它会被加入到接下来的2级(具体需要几级结构也同样结合系统分析)链表中，按照时间顺序在2级链表中排列
  • 接下来2级链表中的操作与上面算法相同，链表中的数据如果再次被访问则移到头部，链表满时，底部数据淘汰

相比LRU，LRU-K需要多维护一个队列，用于记录所有缓存数据被访问的历史，所以需要更多的内存空间来用来构建缓存，但优点也很明显，较好的降低了数据的污染率提高了缓存的命中率，对于系统来说可以用一定的硬件成本来换取系统性能也不失为一种办法。

具体实现

我们要实现一个LRU Cache的话，需要满足什么要求，又要采用什么数据结构？

首先我们要考虑，怎么能让页号在内存里的位置，然后需要考虑LRU淘汰机制

• 如何判断数据是否在缓存里，是否命中？
  • 使用哈希表
• 如何筛选LRU的数据？
  • 我们可以使用链表，把新插入的数据放在表头，更新的数据也放在表头，这样不访问的数据会慢慢聚集到表尾

因此，最后的数据结构应该是一个哈希表和链表的结合——用哈希链地址法，另外做一个链表，把哈希表中所有的节点链起来

如下所示：

• Lru ： 链表的头指针
• Prev/next: 链表的前驱后继指针
• Hash_next:哈希表的后继指针，用来指向value

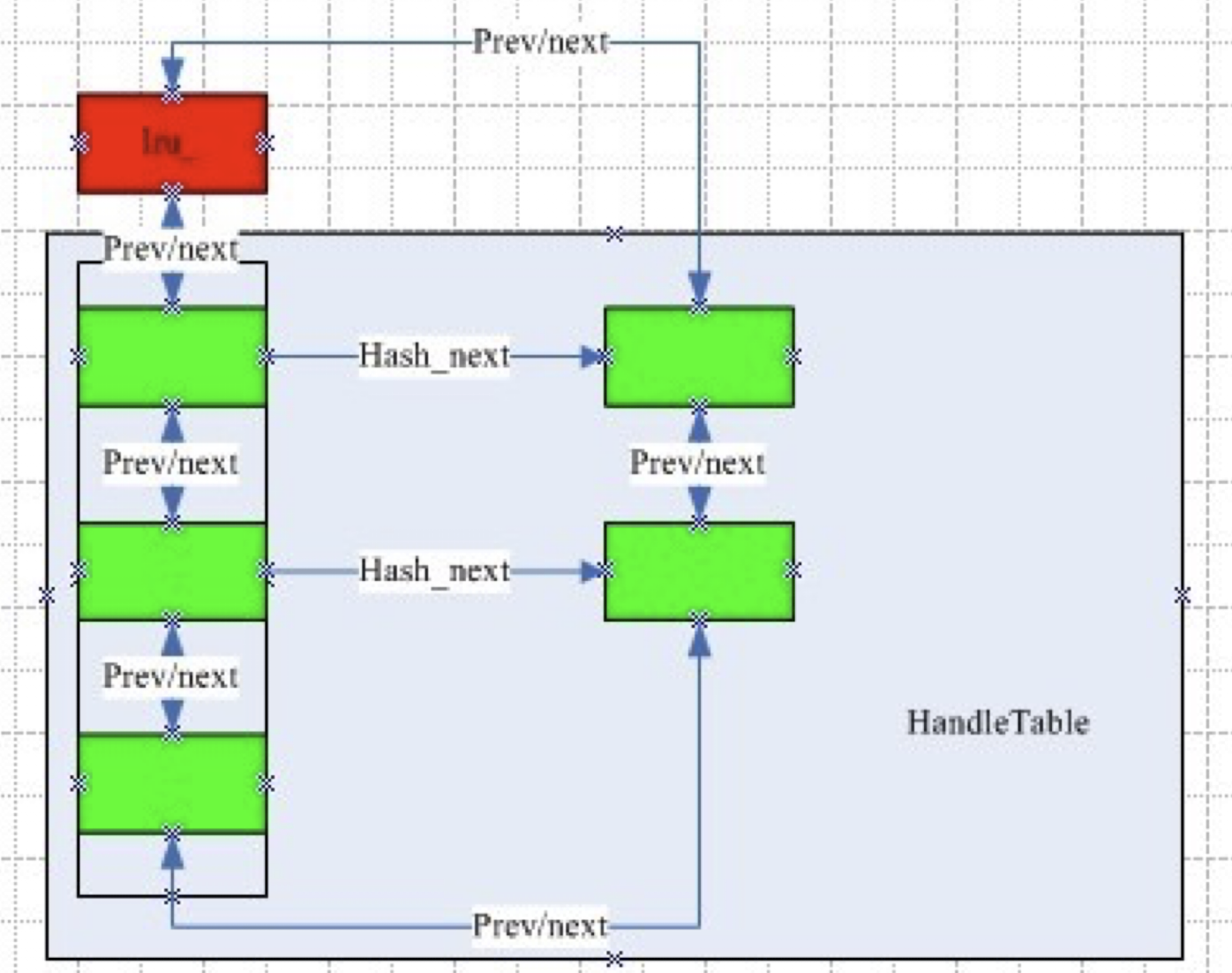
bitcask结构

Log-structured store

事实上，对于数据该如何存储在磁盘中，也非常有门道——之前我们在学习COW B+树时知道顺序写入的性能是要优于随机写入的性能的。

这里我们再介绍一种存储方法——Log-structured 存储，也就是说，将数据像记录日志一样存储在磁盘当中。近些年来，这种存储方式被越来越多的用在数据库存储中。

Log-structured 存储系统的基本单位就是一个只能附加在原有数据之后的日志。每当我想写入新的数据的时候，只需要将其附加到日志的末尾，而不是在磁盘中随变找一个位置。同样的，对meta data也采用这种方式，它的更新也被附加到日志中。这可能看起来效率低下，实际上，每次写入时我们需要更新的索引节点的数量通常非常少。

我们来看一个例子，下面是一个仅包含单个数据项的日志 Foo以及它的索引节点A:

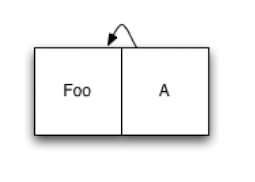
现在，我们要添加第二个元素Bar，将其添加到日志的末尾，然后更新索引条目A’,并将更新后的版本也附加到日志中：

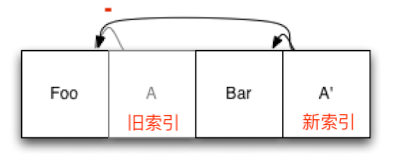
我们看到，旧索引A仍然在日志文件当中，但是不再被使用了。因为他已经被新的索引A’替代。新索引指向Foo和新文件Bar。当上层想要读取我们的文件系统的时候，首先会找到索引的根节点(即A’),然后从根节点出发去寻找其它节点。

接下来我们看看当修改文件的时候会怎么样, 比如说我们修改的是Foo:

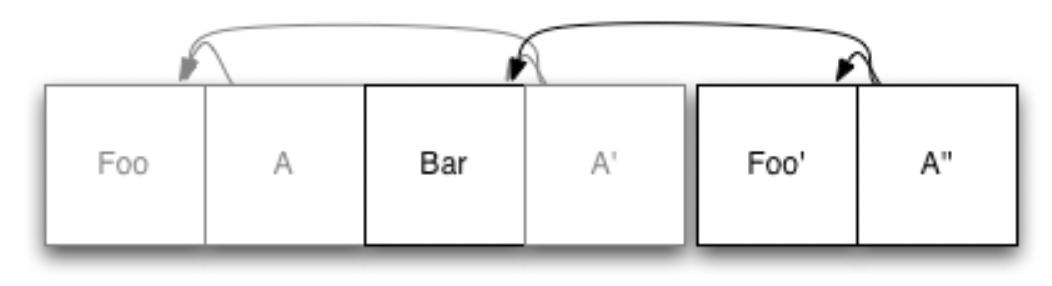
那么首先，修改过后的Foo’ 会被写入日志末尾。然后，我们再次更新索引节点A’ ,变成一个新的A’’,并将其也写在日志末尾。Foo的旧副本会保留在日志当中，但是不会再被新的索引引用.

可以意识到，这个系统并不是可以一直运行下去的，因为无用的文件始终在累计，总有一个时刻我们将耗尽存储空间。因此，在文件系统中，我们将整个磁盘作为一个可以循环的缓冲区，当放不下新的数据的时候，会将旧的日志数据覆盖掉。但在上层看来，新数据就好像是新写入的，而不是覆盖原本数据保存下来的。在常规的文件系统中，随着磁盘越来越满，文件系统需要花费越来越多的时间进行垃圾收集，并将数据写回到日志头部。实际上，当磁盘消耗的存储空间到达80%的时候，文件系统就会停止运行。

但是，我们可以不用这种数据结构来管理文件，我们可以将Log-structured存储用于数据库引擎。也就是说，我们不再底层应用这种模式，而在文件系统的上层来实现它。比如说，我们可以将数据库拆分为多个固定长度的块，那么当我们需要回收一点空间的时候，将有用的数据写在一个块里，删除其他块。比如说对于上面那张图，占用了6页，假设块的大小为4页，我们就可以将其缩短为一个块的大小：

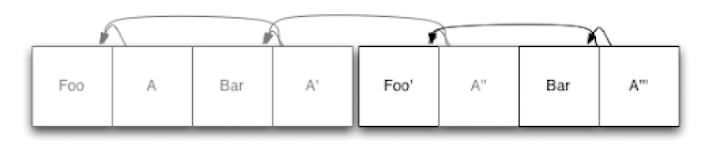
对于上图，第一个日志段完全是空的，因此可以删除。

优势

和底层的文件系统比起来，使用Log-structured存储有以下几个优势：

1. 首先，使用这种存储方式在删除时不需要首先删除最旧的数据——如果中间段几乎是空的话，我们可以对其进行垃圾收集。这对一些需要长时间存放数据的数据库非常有用。
   • 对于何时进行垃圾收集，我们通常可以等到一个段的大部分已经”过期”以后再进行垃圾收集，进一步减少了额外工作量
2. 可以避免重写相同的未修改的数据，因此在这方面可以节省时间，提高性能。
3. 使用这种方法备份也更容易：在传统的B tree上，如果我更新了数据，那么旧的页同时也丢失了；但是使用这种数据结构我们可以通过在完成时将每个新日志段复制到备份介质来连续、增量地备份我们的数据库。如果要恢复，我们根据备份来恢复即可。
4. 使用这个系统的最后一个优势与更好的并发性。我们知道，为了提供事务的一致性(consistency), 大多数数据库会使用复杂的锁系统。根据所需的一致性级别，使用不同的锁。使用锁的缺点就是：当并发量很高时，写入数据相对较低，性能显著下降。
   • 因此，可以使用MVCC(Multiversion Concurrency Control) 来解决这个问题。当一个节点想从数据库读取数据的时候，它会去查找当前的根索引，并将其用于这个节点的事务的剩余部分。因为在一个log-based 系统中，存在的数据永远不会被修改，所以当我们读取了根节点的时候，相当于获取了整个数据库的快照(当前根节点有指向所有可用的数据页的指针)。比如说，我们读取到了A’’’,我们就能读取Foo’和Bar,而其他并发的事务如果对数据进行修改的话，是追加在A’’’之后的，对当前事务并无影响。因此，从这个角度看，我们实现了无锁读取。
   • 在写回数据的时候，我们可以使用Optimistic concurrency(OCC,在高级数据库-事务中有详细介绍)，顾名思义，就是乐观的并发，这和使用锁并等待的悲观机制有所不同。在写入对数据的更改的时候，我们获取写入锁。然后我们要验证当前数据和我们在读取阶段的数据是一致的——我们可以读取索引，判断索引指向的文件是否与之前的相同，地址是否相同。如果相同，说明在这段时间里面并没有发生写入，因此我们可以对其进行追加写；如果不同的话，就发生了事务冲突，我们只需要回滚并从读取阶段重新开始。

bitcask

学习了上面基于日志结构的存储系统，我们现在来学Bitcask架构，也就是日志型的基于哈希表结构的键值对存储系统。比如说Berkeley DB，BeansDB，Ranmcloud都采取了这种架构。 它有以下几个特点：

1. 通过内存中哈希表的key来索引磁盘中数据的位置
2. 数据文件采用追加写的方式
3. 比较低的读写时延。
4. 比较高的随机写吞吐率。
5. 能够控制更大的数据库。
6. 容易备份和恢复。
7. 相对简单，容易理解。
8. 可预计的高访问压力情况。

bitcask只支持追加操作(Append-only)，即所有的写操作只追加而不修改老的数据，每个文件都有一定的大小限制，当文件增加到相应的大小，就会产生一个新的文件，老的文件只读不写。在任意时刻，只有一个文件是可写的，用于追加数据，被称为活跃数据文件(active data file)，其他已经达到文件大小限制的，被称为老数据文件(older data file)。

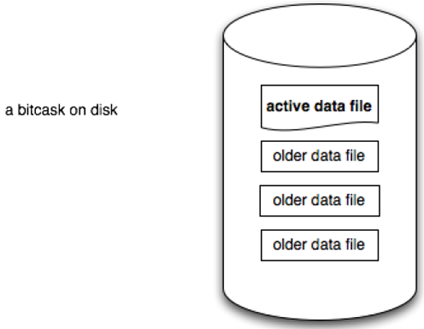
活跃数据文件仅支持追加写入，因此所有的写入操作都是串形化的而不用磁盘随机定位。写入的键值对格式如下：

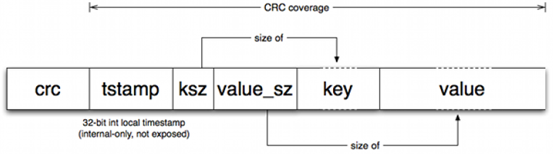
1. crc用于验证
2. timestamp 时间戳
3. key size : 键的长度
4. value size:值的长度
5. key 数据
6. Value 数据

哈希索引

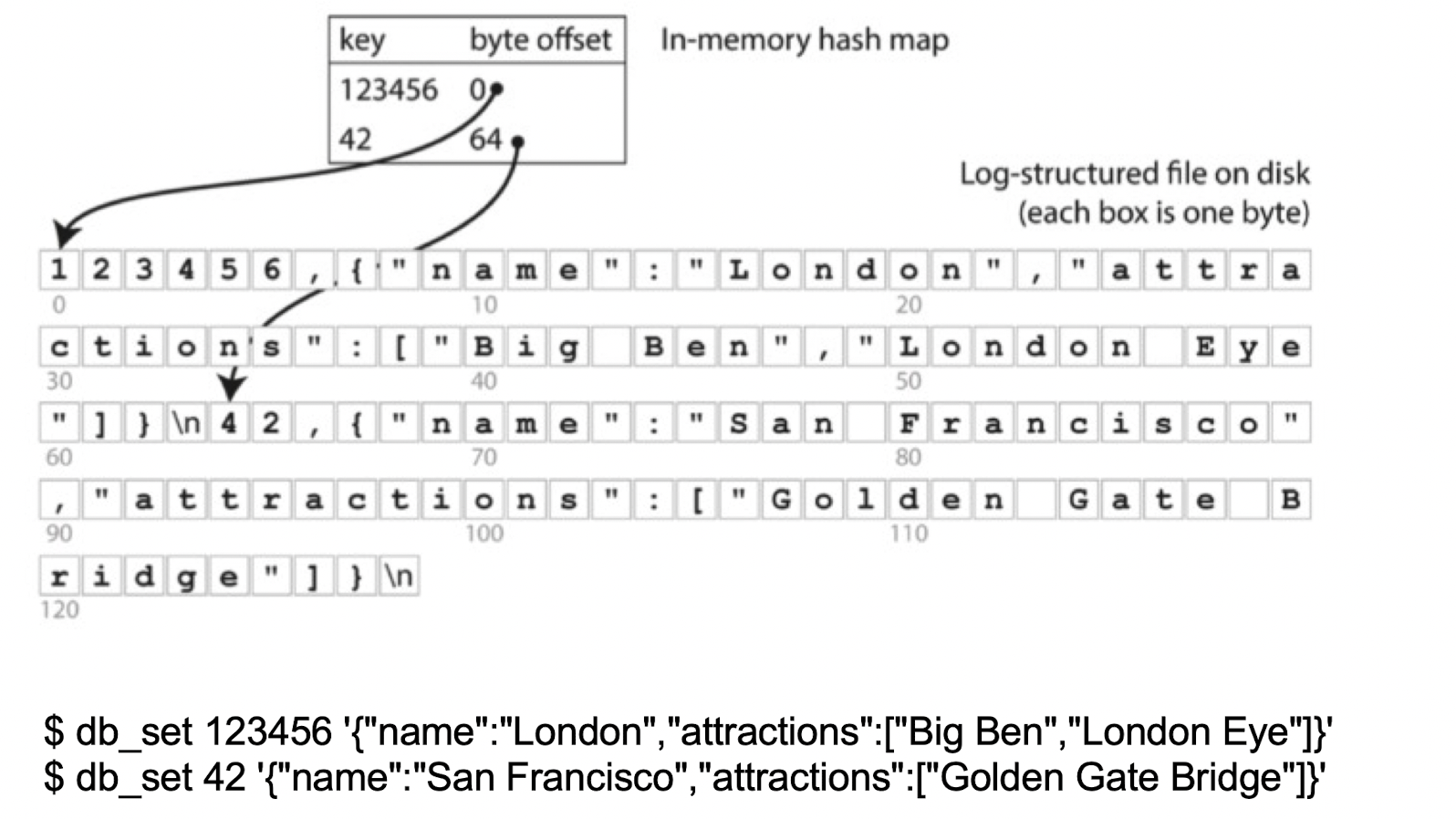
在bitcask模型中，使用了Hash表的索引结构。在内存中有一张哈希表，通过哈希表中的key值可以快速地定位到磁盘中的数据，大致结构如下所示：

hash表对应的这个结构中包括了三个用于定位数据value的信息，分别是文件id号(file_id)，value值在文件中的位置（value_pos）,value值的大小（value_sz），于是我们通过读取file_id对应文件的value_pos开始的value_sz个字节，就得到了我们需要的value值。整个过程如下图所示：

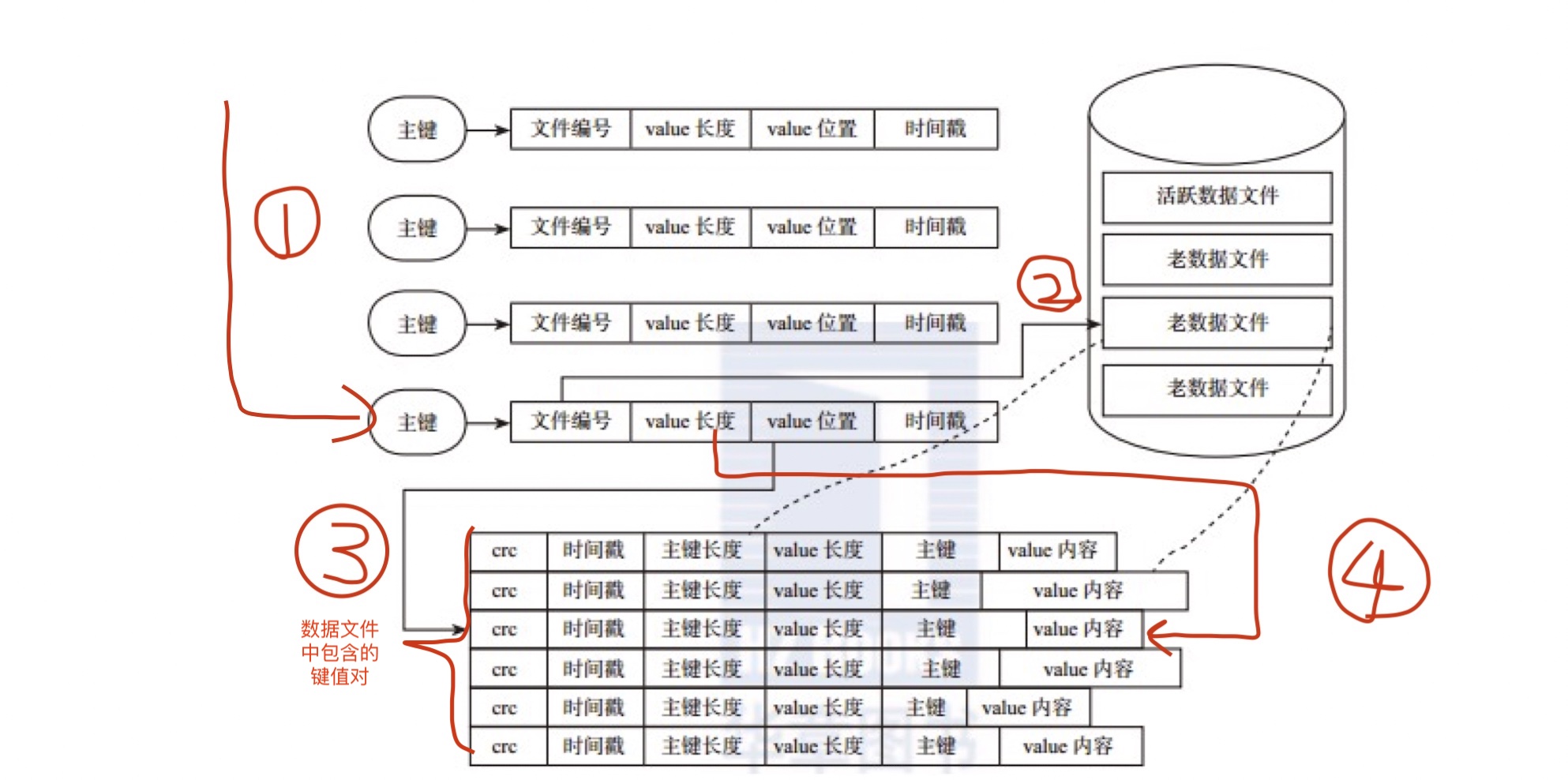
在一个具体的哈希索引例子中，我们可以更清楚的看到数据是如何被找到的：

文件的merge

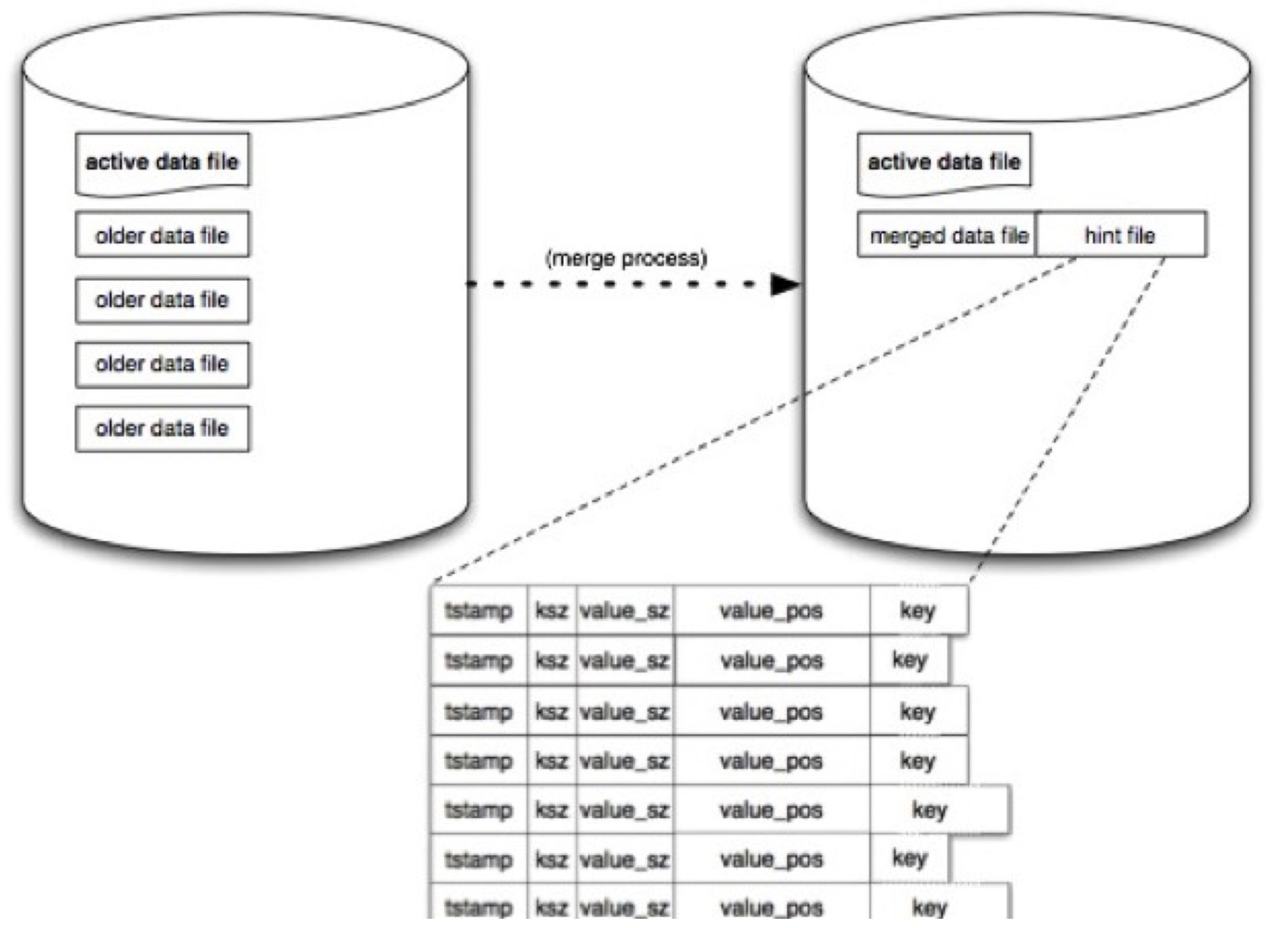
合并操作是定时对所有的旧数据文件进行扫描并生成新的数据文件（其本质是将同一个Key的多个操作进行合并。）在这个过程中，并没有包含active date file，因为它还还在不停写入。

键值对的删除也是追加写的方式写入活动数据文件中，真正的删除会在下一次的数据合并中进行。

这里的merge其实就是将对同一个key的多个操作以只保留最新原则进行删除。每次merge之后，新生成的数据文件就不再有冗余了。如下图所示：对于yawn,保留最新的511；对于scratch，保留最新的252；对于mew，保留最新的1087；对purr，保留最新的2114

容量限制

我们假设内存是有限的，磁盘空间是无限的。可以给出一个元数据的格式：

//BeansDB文件元数据格式
struct t_item {
	unit32_t pos;	//数据记录在
	int32_t ver;	//数据记录版本号
	unit16_t hash;//数据记录hash
	unit8_t length;//key的长度
	char key[1];	//key的实际值
}

beansDB将pos的低8位用来存储文件的id，这样一便可以最多存储256个文件。然后用剩下的24位用来存储文件内偏移。每个文件的大小一般被定义为2GB,因此该系统最大支持的存储空间为512GB。每个文件元数据占据内存的总存储空间为：4B+4B+2B+1B+size(key), 按照size(key) = 20B来计算。 100M(20*100*1024)个文件也只会占用2GB的内存。

容错

从上面我们可以知道，索引的Hash表存放在内存中，如果发生系统重启，则须要扫描磁盘中的数据重建Hash表，如果数据量非常大，这个过程是非常耗时的。也就是说，bitcask启动速度是很慢的。 因此，bitcask模型中还要对older data file生成一个hint file，在这处文件中，数据结构与磁盘中的数据文件非常相似，不同的是 , 它不存储具体的value值，而是存储value的位置信息。相当于对旧数据哈希表的物化。其结构如下图：

LSM Tree 架构存储

Skiplist

在简单的链表中，如果我们要在里面找到一个元素的话，需要将整个链表都遍历一次。因此我们可以设计一种新型的链表——skiplist(跳表), 来提高查询的效率。跳表的平均期望的查找、插入、删除时间复杂度都是$O(\log n)$ ，n代表跳表的长度。

许多知名的开源软件（库）中的数据结构均采用了跳表这种数据结构。

• Redis中的有序集合zset
• LevelDB、RocksDB、HBase中Memtable
• ApacheLucene中的TermDictionary、Posting List

skiplist的构建

首先我们不满足只有一层的链表，那么我们是不是可以在原有链表的基础上增加一层？加入我们每相邻两个节点来增加一个指针，让指针去指向下下个节点，如下图：

这样一来，第二层包含的节点数只有原来的一半。现在，当我们想要查找数据的时候，可以先沿着第二层的链表进行查找。当碰到比待查数据大的节点时，再回到原来的链表中进行查找。比如我想查找23，就是这样一个查找路径：

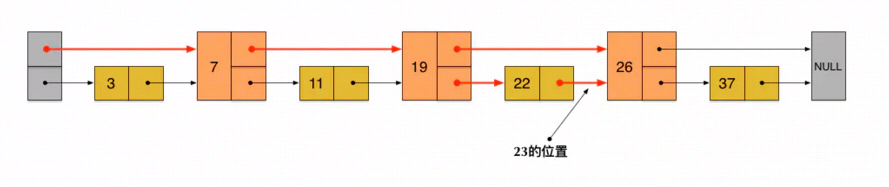
• 首先，23和7比较，再和19比较，比它们都大；继续向后比较，发现比26小，因此要掉到下面的链表(L0)
• 在L0中，从19开始，23比22要大；那么继续向后比较
• 发现23比26小，说明待查数据23在原链表中不存在

我们发现，在这个查找过程中，由于新增加的指针，我们不需要与链表中的每个节点去逐个进行比较了。需要比较的节点数大概只有原来的一半。

因此，我们可以采用同样的方式再往上加一层，产生第三层链表L2

在这个新的三层链表结构上，如果我们还是查找23，那么：

• 沿着最上层链表首先要比较的是19，发现23比19大，但19已经是L2的最后一层了，因此跳到L1
• 查找方式如二层跳表。

可以想象，当链表足够长的时候，这种多层链表的查找方式能让我们跳过很多下层节点，大大加快查找的速度

Skiplist就是根据这种思想而设计出来的。但是，如果我们按照上面的这种方法来构建跳表，在新插入一个节点之后，就会打乱上下相邻两层链表上节点个数严格2:1的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新退化成O(n)。

因此跳表引入了一个很好的机制。为了避免这种情况的发生，它不要求上下两层链表之间的节点个数严格满足1:2, 而是在生成上层链表的时候，会给每一个节点”抛硬币”——假设抛到正面就会上升一层，抛到反面就按兵不动。

一般来说，跳表的高度是$\log(n)$ ，n为链表中元素个数。最终结果如下：

skiplist的查找

Skiplist的查找和上面所说的方法基本是一样的，即从高层向底层查找，不断缩小范围，最后锁定目标。

skiplist的插入

skiplist的插入是需要一定的技巧的

首先是进行查找，比如对上面这张跳表，我想插入15。那么我们首先要查找到15该插入的位置，同时记录每一层的小于插入值的最大节点，比如在L2，15处于6和25之间，我们就将6保存下来，之后有用。

在这里我们保留每个红色箭头的起始节点:

层数	保留节点
L3	6
L2	6
L1	9
L0	12

经过了查找，我们知道15应该插入到12到17 中间，那么问题来了——15节点的层数应该是多少？

这里我们还是采用随机的方法，对15节点抛硬币，逻辑如下

• 如果是正面，那么就加一层，并继续抛硬币；
  • 如果还是正面，就继续抛，一直到最高层
  • 如果是反面，就立刻停止
• 如果是反面，那么就不再增加层数了。

最后，假设15节点的层高为3，那么就需要先断开三层链表，并进行重连该节点的前后指针。

伪代码如下：

• 首先，每个节点肯定都有第1层指针（每个节点都在第1层链表里）
• 如果一个节点有第i层(i>=1)指针（即节点已经在第1层到第i层链表中），那么它有第(i+1)层指针的概率为p
• 节点最大的层数不允许超过一个最大值，记为MaxLevel
  这个计算随机层数的伪码如下所示：

randomLevel()
    level := 1
    // random()返回一个[0...1)的随机数
    while random() < p and level < MaxLevel do
        level := level + 1
    return level

skiplist的删除

删除和插入一样，首先要进行查找，同时记录每个前驱结点，因为在删除L0节点之后需要断开上面几层的指针

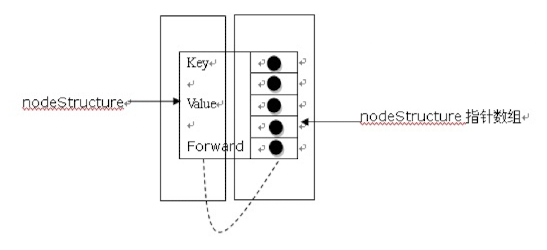
skiplist每个点的结构

typedef struct nodeStructure *node;
typedef struct nodeStructure
{
  keyType key; 			// key值
  valueType value;  // value值
  // 向前指针数组，根据该节点层数的不同指向不同大小的数组
  node forward[1]; 	// 这是一个指针数组首地址，实际分配内存大小时多于一个
}

// newNodeOfLevel生成一个nodeStructure结构体，同时生成l个node* 数组指针
#define newNodeOfLevel(l) (node)malloc(sizeof(struct nodeStructure)+(l)*sizeof(node *));

注意，节点其实只有一层，而不是多层链表

算法分析

在这一部分，我们来简单分析一下skiplist的时间复杂度和空间复杂度，以便对于skiplist的性能有一个直观的了解。

我们先来计算一下每个节点所包含的平均指针数目（概率期望）。节点包含的指针数目，相当于这个算法在空间上的额外开销(overhead)，可以用来度量空间复杂度

平均指针数目

根据前面randomLevel()的伪码，我们很容易看出，产生越高的节点层数，概率越低。定量的分析如下：

• 节点层数至少为1。而大于1的节点层数，满足一个概率分布
• 节点层数恰好等于1的概率为$1-p$
• 节点层数大于等于2的概率为$p$，而节点层数恰好等于2的概率为$p(1-p)$
• 节点层数大于等于3的概率为$p^2$，而节点层数恰好等于3的概率为$p^2(1-p)$
• 节点层数大于等于4的概率为$p^3$，而节点层数恰好等于4的概率为$p^3(1-p)$

一般来说我们取$p=0.5$

因此，一个节点的平均层数（也即包含的平均指针数目），计算如下：

$$1\times(1-p)+2p(1-p)+3p^2(1-p) +...=(1-p)\sum_{k=1}^{+\infty}kp^{k-1}\\ \sum_{k=1}^{+\infty}\int kp^{k-1}d_k = \sum_{k=1}^{\infty}p^k =p(\frac{1-p^k}{1-p}) = \frac{1}{1-p}-1\\$$

再对积分求导数，可得:

$$1\times(1-p)+2p(1-p)+3p^2(1-p) +...=(1-p)\sum_{k=1}^\infty kp^{k-1} = (1-p)\frac{1}{(1-p)^2} = \frac{1}{1-p}$$

现在很容易计算出：

• 当p=1/2时，每个节点所包含的平均指针数目为2；
• 当p=1/4时，每个节点所包含的平均指针数目为1.33。这也是Redis里的skiplist实现在空间上的开销。

时间复杂度

接下来，为了分析时间复杂度，我们计算一下skiplist的平均查找长度。查找长度指的是查找路径上跨越的跳数，而查找过程中的比较次数就等于查找长度加1。

为了计算查找长度，这里我们需要利用一点小技巧。我们注意到，每个节点插入的时候，它的层数是由随机函数randomLevel()计算出来的，而且随机的计算不依赖于其它节点，每次插入过程都是完全独立的。所以，从统计上来说，一个skiplist结构的形成与节点的插入顺序无关

这样的话，为了计算查找长度，我们可以将查找过程倒过来看，从右下方第1层上最后到达的那个节点开始，沿着查找路径向左向上回溯，类似于爬楼梯的过程。我们假设当回溯到某个节点的时候，它才被插入，这虽然相当于改变了节点的插入顺序，但从统计上不影响整个skiplist的形成结构

现在假设我们从一个层数为i的节点x出发，需要向左向上攀爬k层。这时我们有两种可能：

• 如果节点x有第(i+1)层指针，那么我们需要向上走。这种情况概率为p
• 如果节点x没有第(i+1)层指针，那么我们需要向左走。这种情况概率为(1-p)

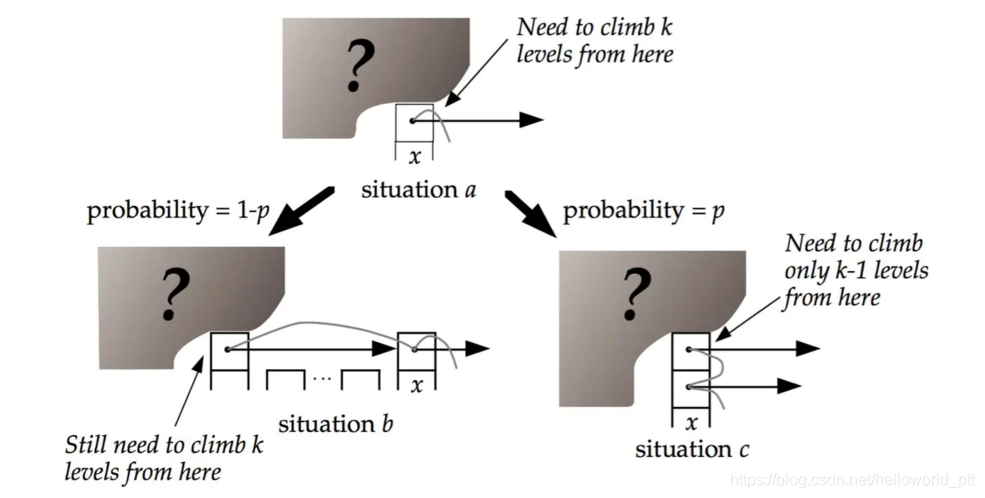
用C(k)表示向上攀爬k个层级所需要走过的平均查找路径长度（概率期望），那么：

C(0)=0C(k)=(1-p)×(上图中情况b的查找长度) + p×(上图中情况c的查找长度)
1

代入，得到一个差分方程并化简：

C(k)=(1-p)(C(k)+1) + p(C(k-1)+1) 
C(k)=1/p+C(k-1) 
C(k)=k/p

这个结果的意思是，我们每爬升1个层级，需要在查找路径上走 1/p 步。而我们总共需要攀爬的层级数等于整个skiplist的总层数-1。

那么接下来我们需要分析一下当skiplist中有n个节点的时候，它的总层数的概率均值是多少。这个问题直观上比较好理解。根据节点的层数随机算法，容易得出：

• 第1层链表固定有$n$个节点；
• 第2层链表平均有$n\times p$个节点；
• 第3层链表平均有$n\times p^2$个节点；

所以，从第1层到最高层，各层链表的平均节点数是一个指数递减的等比数列。容易推算出，总层数的均值为$\log\frac{1}{pn}$，而最高层的平均节点数为$1/p$。

综上，粗略来计算的话，平均查找长度约等于 $C(\log\frac{1}{pn-1}) = \frac{\log 1/(pn-1)}{p}$ ，也就是时间复杂度为 $O(log(n))$

Skiplist和B树以及哈希表的对比

• skiplist和各种平衡树（如AVL、红黑树等）的元素是有序排列的，而哈希表不是有序的。因此，在哈希表上只能做单个key的查找，不适宜做范围查找。 所谓范围查找，指的是查找那些大小在指定的两个值之间的所有节点
• 在做范围查找的时候，平衡树比skiplist操作要复杂。
  • 在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。
  • 而在skiplist上进行范围查找就非常简单，只需要在找到小值之后，对第1层链表进行若干步的遍历就可以实现
• 平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而skiplist的插入和删除只需要修改相邻节点的指针，操作简单又快速
• 从内存占用上来说，skiplist比平衡树更灵活一些。一般来说，平衡树每个节点包含2个指针（分别指向左右子树），而skiplist每个节点包含的指针数目平均为1/(1-p)，具体取决于参数p的大小。如果像Redis里的实现一样，取p=1/4，那么平均每个节点包含1.33个指针，比平衡树更有优势
• 查找单个key，skiplist和平衡树的时间复杂度都为$O(\log n)$，大体相当；而哈希表在保持较低的哈希值冲突概率的前提下，查找时间复杂度接近O(1)，性能更高一些。所以我们平常使用的各种Map或dictionary结构，大都是基于哈希表实现的
• 从算法实现难度上来比较，skiplist比平衡树要简单得多

Log-structured Merge Tree Model

LSM的基本思想是将修改的数据保存在内存，达到一定数量后在将修改的数据批量写入磁盘，在写入的过程中与之前已经存在的数据做合并。同B树存储模型一样，LSM存储模型也支持增、删、读、改以及顺序扫描操作。LSM模型利用批量写入解决了随机写入的问题，虽然牺牲了部分读的性能，但是大大提高了写的性能。

下图是LSM 树存储模型的基本架构：

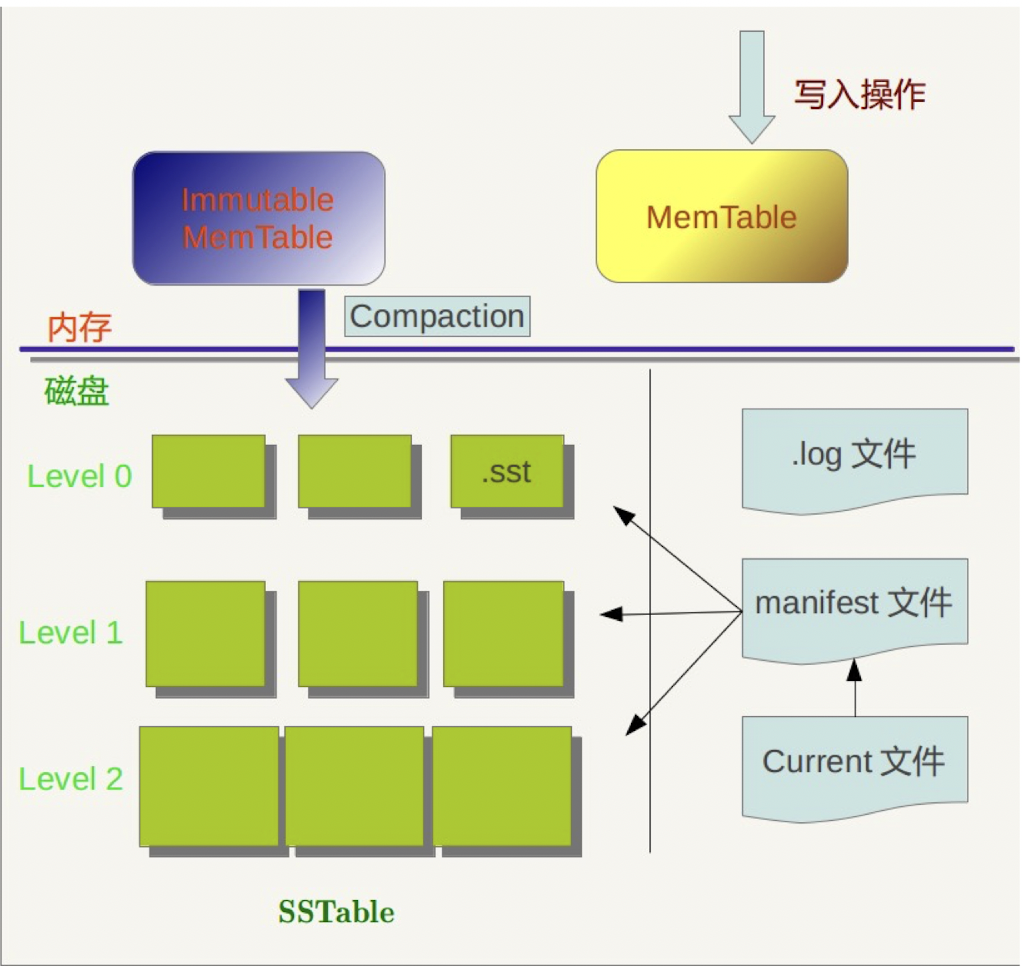
我们需要了解三个最重要的组件：MemTable，Immutable MemTable和SSTable

Memtable

LSM本身由MemTable,Immutable MemTable,SSTable等多个部分组成，其中MemTable位于内存，用于记录最近修改的数据，一般用跳跃表来组织(也可以用平衡树)。当MemTable达到一定大小后，将其冻结起来变成Immutable MemTable，然后开辟一个新的MemTable用来记录新的记录。而Immutable MemTable则等待转存到磁盘。

Immutable MemTable

顾名思义，就是只能读不能写的内存表。内存部分已经有了MemTable，为什么还要使用Immutable MemTable？个人认为其原因是为了不阻塞写操作。因为转存的过程中必然要保证内存表的记录不变，否则如果新插入的记录夹在两条已经转存到磁盘的记录中间，处理上会很麻烦，转存期间势必要锁住全表，这样一来就会阻塞写操作。所以不如将原有的MemTable变成只读Immutable MemTable,再开辟一个新的MemTable用于写入，即简单，又不影响写操作。

SSTable

SSTable是本意是指有序的键值对集合( a set of sorted key-value pairs )。是一个简单有用的集合，正如它的名字一样，它存储的就是一系列的键值对。当文件较大的时候，还可以为其建立一个键-值的位置的索引，指明每个键在SSTable文件中的偏移距离。这样可以加速在SSTable中的查询。

使用MemTable和SSTable这两个组件，可以构建一个最简单的LSM存储模型。这个模型与Bitcask模型相比，不存在启动时间长的问题，但是这个模型的读性能非常差。在之后会详细展开

读写操作

• 读取操作

之前我们说了在LSMT中，读取数据的性能会很差。因为一但在MemTable找不到相应的键，则需要在根据SSTable文件生成的时间，从最近到较早在SSTable中寻找，如果都不存在的话，则会遍历完所有的SSTable文件。因此，如果SSTable文件个数很多或者没有建立SSTable的文件内索引的话，读性能则会大大下降。

除了在对SSTable内部建立索引外，还可以使用Bloom Filter, 提高Key不在SSTable的判定速度。同样，定期合并旧的SSTable文件，在减少存储的空间的同时，也能提高读取的速度。 正如上图所示，SSTable分为好多层，Level1就是由Level0合并而来的，而Level2也是由Level1合并而来的。

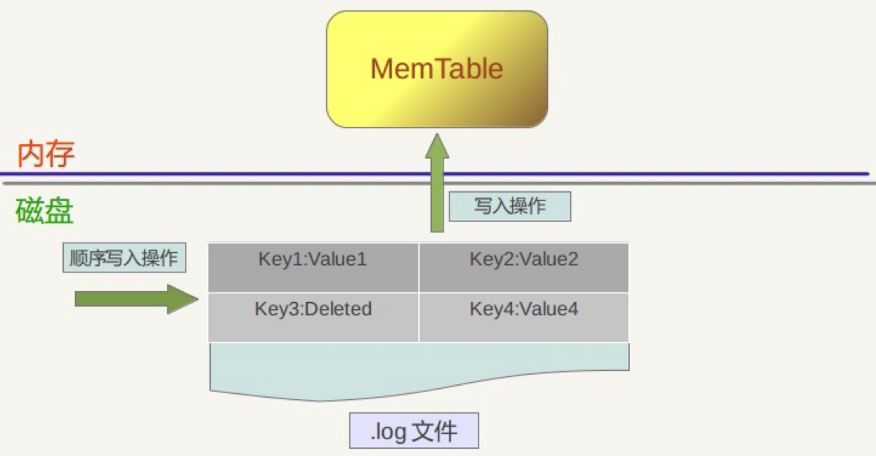
• 写入操作

1. 首先，将这条KV记录以顺序写的方式追加到log文件末尾
2. 如果写入log文件成功，那么这条KV记录插入内存中的Memtable中
3. SklipList先查找合适的插入位置，然后修改相应的链接指针将新纪录插入即可

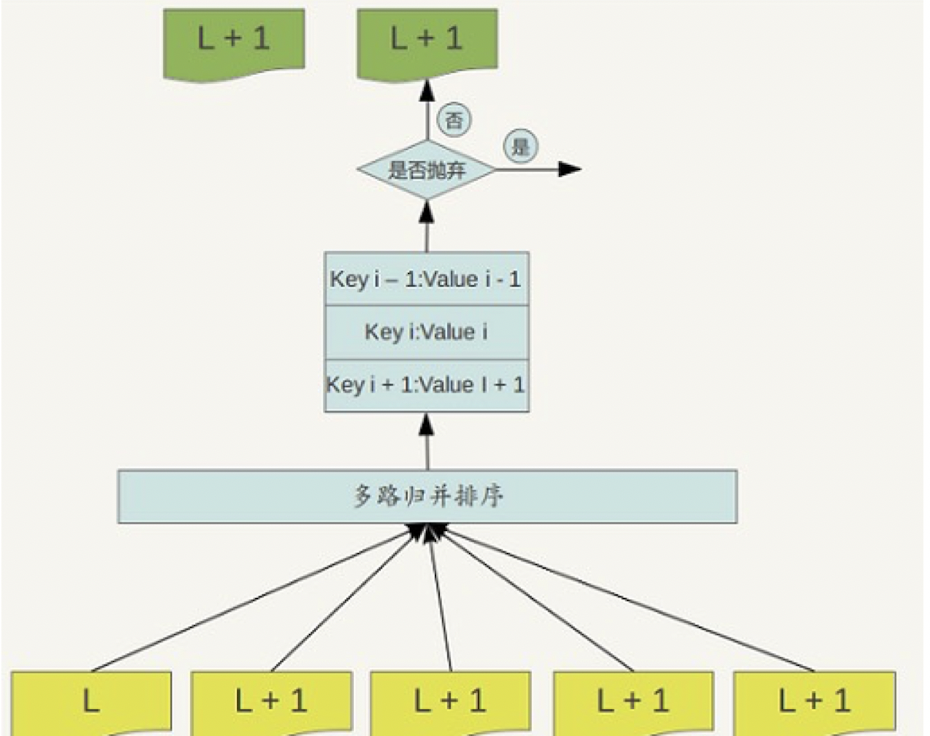
Compation操作

• Minor compaction：当内存中的memtable大小到了一定值的时候，将内容保存到磁盘文件中
• Major compaction: 对多个文件中的所有记录重新进行排序。也就是Level0向Level1，Level1向Level2的转变过程

在最本章的最后一节我们会详细学习两种操作的具体内容。

LevelDB 的 SSTable结构

上面整体整体了一下LSMT中的SSTable，现在我们来看一下其内部结构：

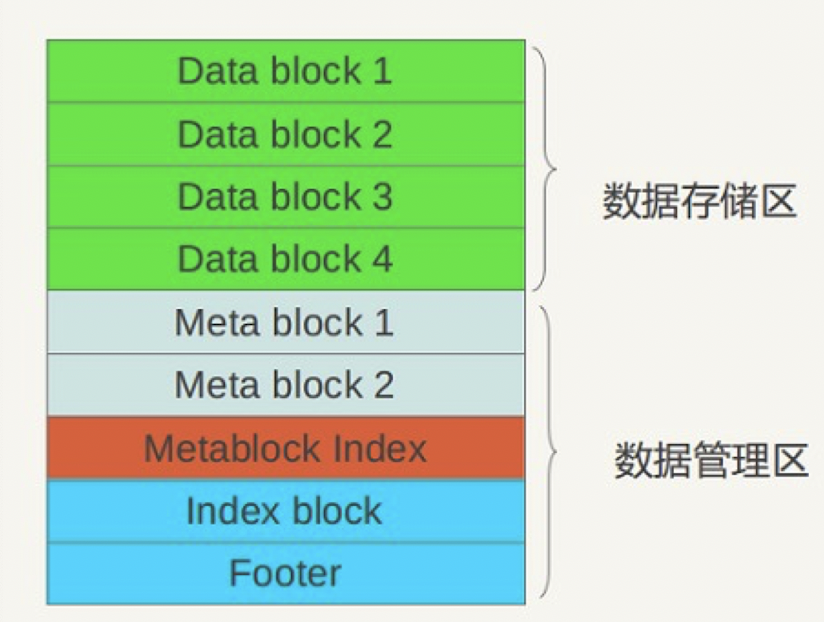
从逻辑布局角度看：可以将.sst文件划分为数据存储区和数据管理区，数据存储区存放实际的kv数据，数据管理区则提供一些索引指针等管理数据，目的是更快速便捷地查找相应记录。

• DataBlock: 存储 Key-Value记录，分为data,type, CRC 三部分
• MetaBlock：索引DataBlock的元数据块
• MetaBlock_index： 记录 Filter的相关信息
• IndexBlock：描述一个DataBlock，存储着对应DataBlock的最大Key值，DataBlock在.sst文件中的偏移量和大小
• Footer：索引的索引，记录IndexBlock和MetaIndexBlock在SSTable中的偏移量和大小

Footer

我们先从索引的索引Footer说起，它记录IndexBlock和MetaIndexBlock在SSTable中的偏移量和大小。其结构如下：

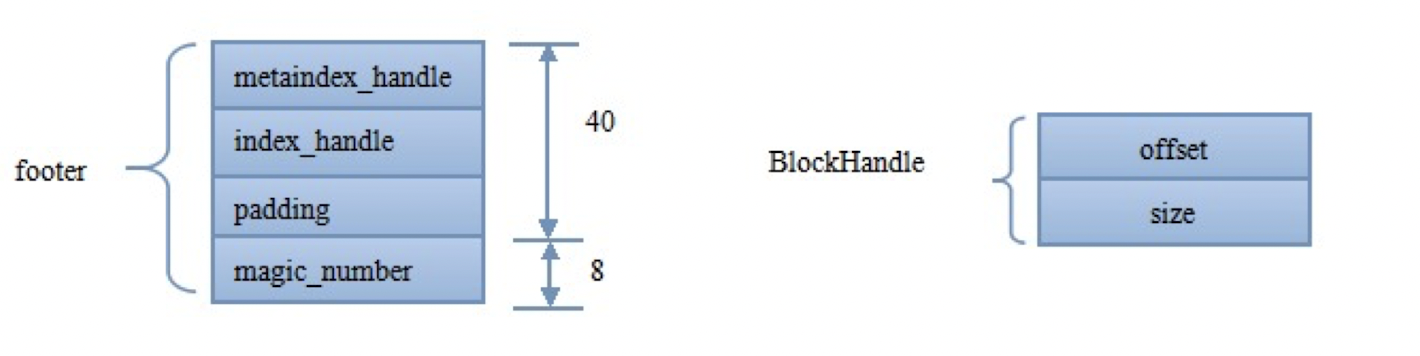
Footer位于SSTable的尾部，占用48个字节。 其中，最主要的就是metaindex_handle和index_handle两个信息。

metaindex_handle与index_handle物理上占用了40个字节。每一个handle的结构如右图，逻辑上就是offset+size(大小和偏移量)，在内存中占用16个字节。因此，两个handle的实际存储可能不到32个字节，剩下是一些padding填充。

DataBlock

数据块主要分为数据、重启点、尾部三个部分

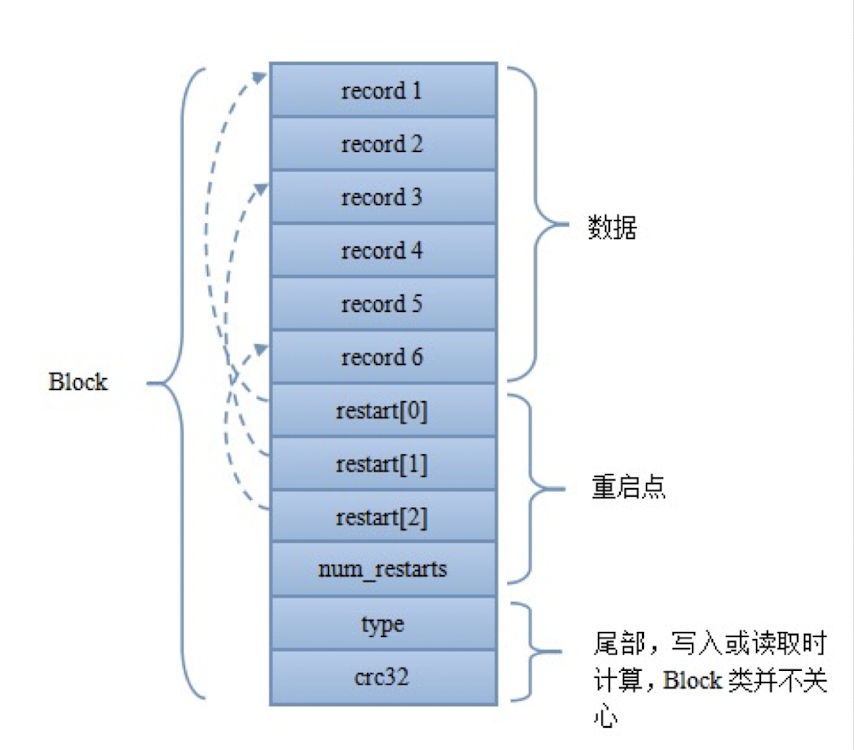
• 每个Record的格式如下所示：

我们发现，里面有key共享长度和key非共享长度，这是为什么？

事实上LevelDB做了一些存储上的优化：在DataBlock中，key是有序存储的，相邻的key之间是可能有重复的，因此存储时采用前缀压缩，后一个key只存与前一个key不同的部分。因此出现了共享长度和非共享长度。比如说，Record1是 abcd，Record2是abce，那么共享长度就是abc, 非共享长度就是d和e。

• 重启点我们看到是一个数组的形式，其指向的位置就表示该key不按前缀压缩，而是完整存储的key值。除了减少压缩空间之外，重启点的第二个作用就是加速读取，更快的读取！一般来说一个Block大小为4K，里面可能包含了很多Record。重启点可以通过二分的方法来定位具体的重启点位置，进一步减少了需要读取的数据。如果不设重启点，那么将Block读进内存之后，要找一个特定的record只能通过顺序搜索实现，影响性能

• 尾部主要分为type和crc。这里的CRC即循环冗余校验码 ( Cyclic Redundancy Check ）：是数据通信领域中最常用的一种查错校验码，其特征是信息字段和校验宇段的长度可以任意选定。循环元余检查（CRC）是一种数
  据传输检错功能，对数据进行多项式计算，并将得到的结果附在帧的后面，接收设备也执行类似的算法 ，以保证数据传输的正确性和完整性。在Sstable中， 写数据时生成CRC， 读时进行校验

Data Index Block

因为一个DataBlock的大小只有4KB，但是一个SSTable的大小可能有16MB，因此里面包含了许多DataBlock。将其全部加载到内存里并顺序找过来肯定是不现实的。 因此SSTable中设计了Data Index Block,然后用来实现对DataBlock的二分查找。在查找时，先将Data Index Block其加载到内存中，然后再去磁盘中读取想要的DataBlock

因为我们在DataBlock中，Key都是按照顺序存储的。理论上，只要保存了每个块中最大的Key，就可以实现二分查找，但是LevelDB在这里做了个优化：

它并非保存最大的Key，而是保存了一个能分隔两个DataBlock的最短Key。比如，假定DataBlock1的最后一个Key为 abcdefg , DataBlock2的第一个Key为 abzxcv , 那么，index就可以记录DataBlock1的索引Key为：abd。这样的分割串可能有很多，只要保证DataBlock1中的所有key都小于等于此索引，DataBlock2中所有Key都大于此索引即可。这种优化缩减了索引长度，查询时可以有效减少比较次数

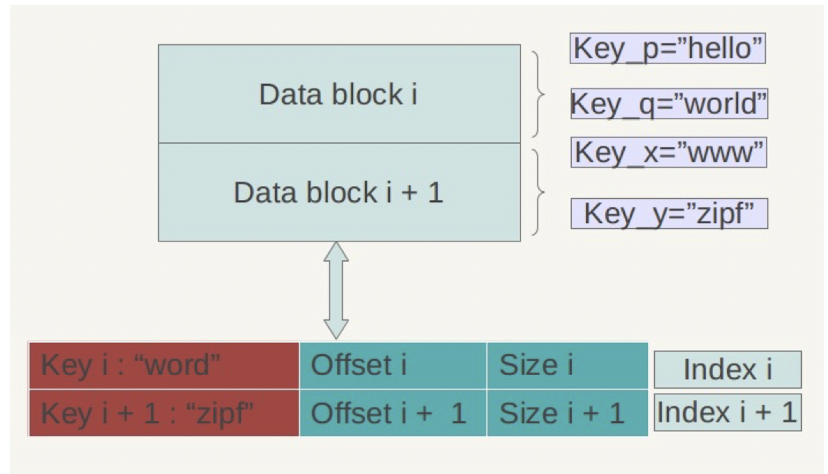
我们再举一个例子，如上图，DataBlock1 的最后一个索引是world, DataBlock2的第一个索引是www，我们可以令DataBlock1的索引为 word ，因为 world<word<www

最后，我们将上面讲的综合起来，写成一个细致的SSTable结构：

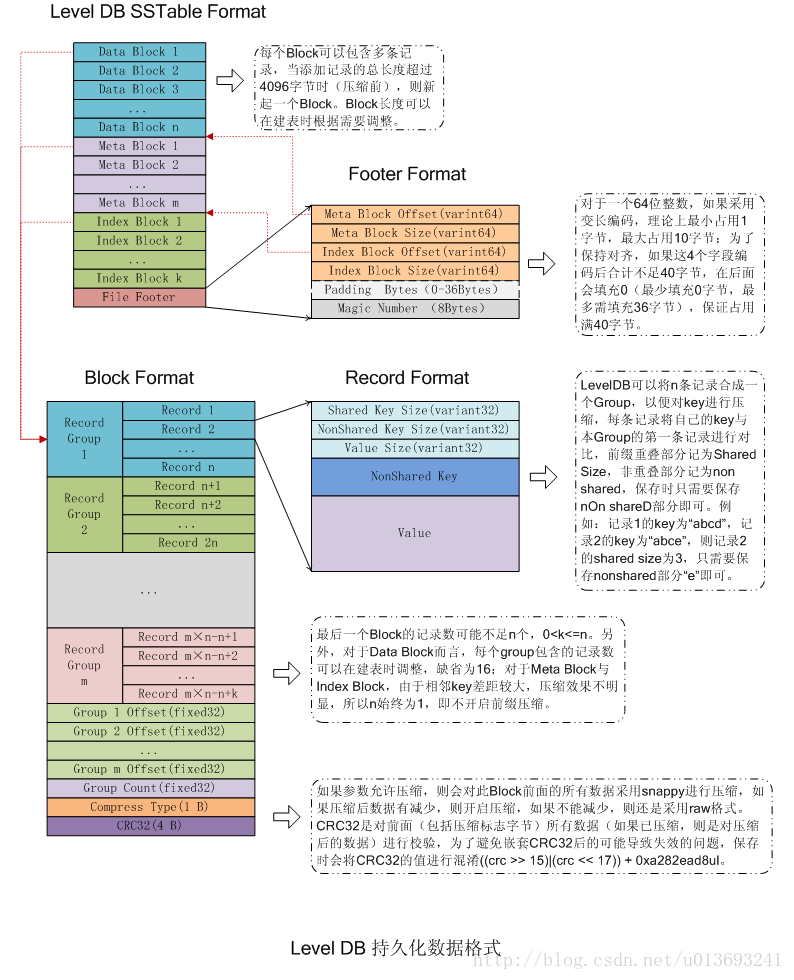
SSTable文件管理

在这一块我们来介绍文件合并的相关流程。

文件管理模块

首先，我们要知道每个SSTable都是一个文件。因此有一个文件信息的结构 FileMetaData

struct FileMetaData {
    int refs:								
    int allowed seeks:			// Seeks allowed until compaction
    uint64 + number;
    uint64t file size;			// File size in bytes
    Internalkey smallest;		// Smallest internal key served by table
    Internalkey largest;		// Largest internal key served by table

	FileMetaData() : refs(0), allowed seeks (1 << 30), file size(0) { }
};

文件在写入的时候会存在许许多多个版本，因此一个可以进行文件管理的模块是非常重要的

我们引入Version，Version Edit 和Version Set 三个概念：

Version

每次的文件融合，都会使得SSTable发生变化，每个SSTable的状态，我们称之为一个Version.

Version包含了什么东西？其实，只要记录当前版本的文件信息即可：

std::vector <FileMetaData*> //有几层数组就有多长
files_[config::kNumLevels];

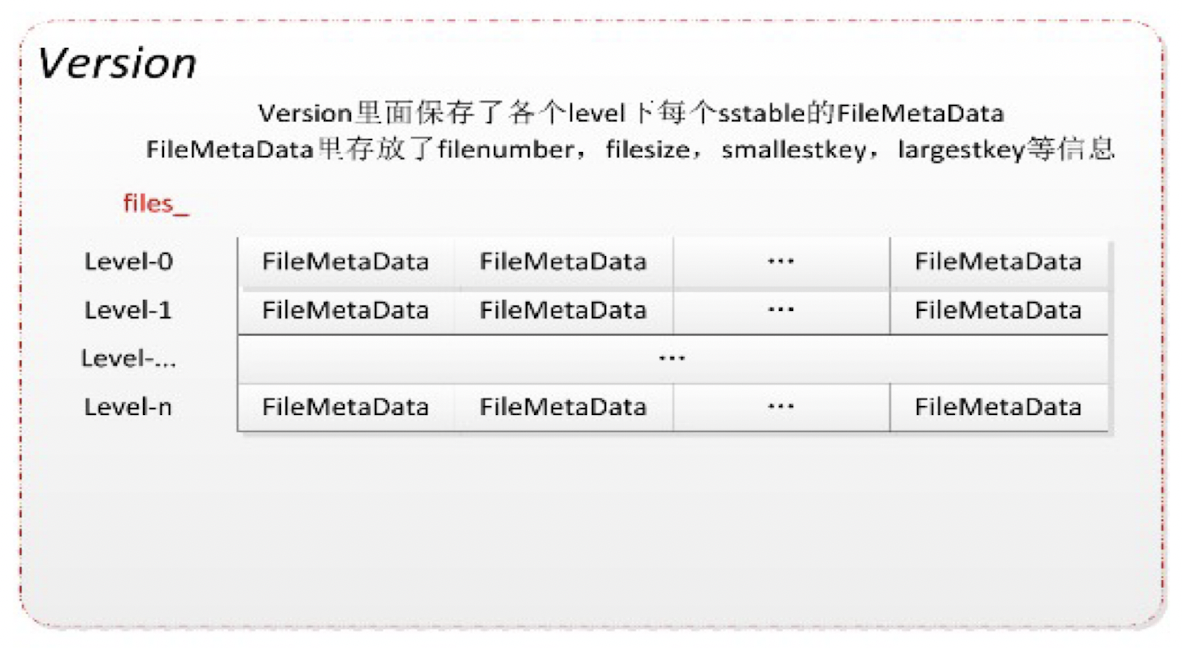
我们看到，其实version就是存储了文件信息的二维数组。为什么是数组？因为SSTable有好几层，每一层的状态都需要被记录下来。

Version Edit

既然Version是保留文件信息的，那么当SSTable发生变化的时候，就需要这样一个文件来记录变化的内容。这个文件就是Version Edit.

其主要元素 就是：删除的文件，以及新产生的文件

DeletedFileSet deleted_files_;//删除的文件
std::vector<std::pair<int, FileMetaData>>new_files_;//新产生的文件

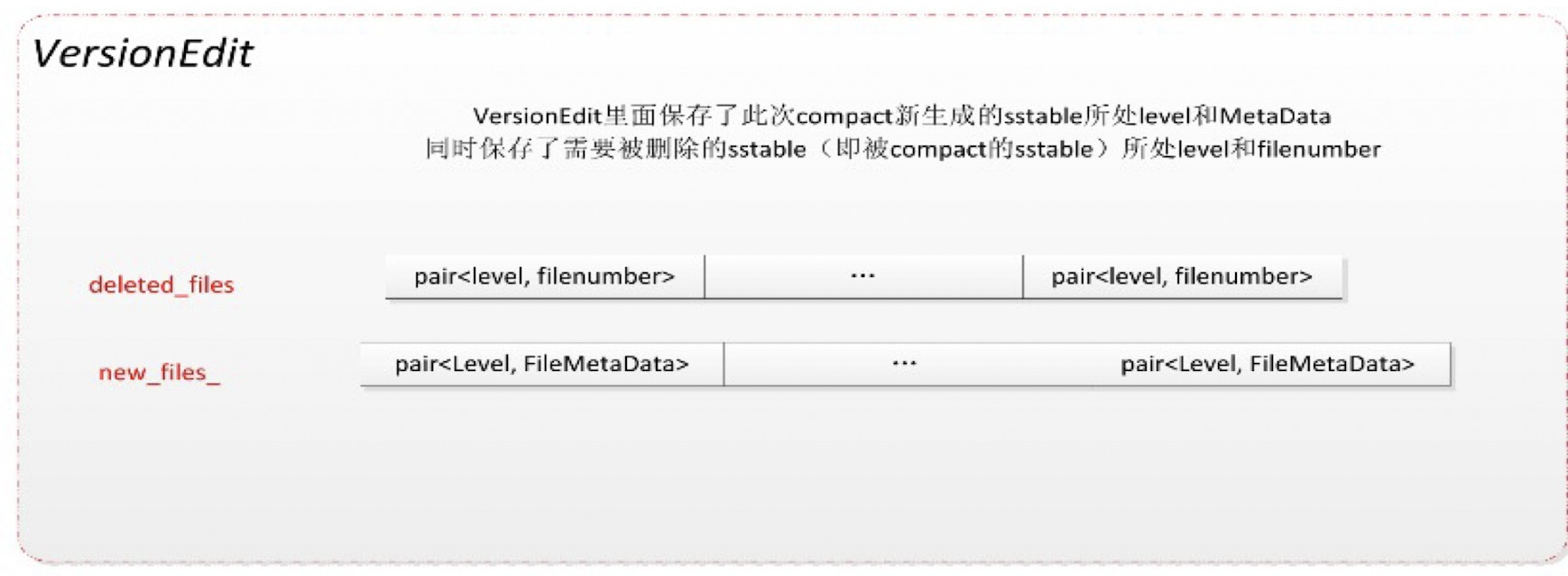
Version之间是通过增量的方式演进的，而两个Version之间的差异就称之为一个Version Edit ： Version0+VersionEdit = Version1

Version Set

从旧的到新的所有Version都存储在Version Set当中，所以，Version Set可以理解为一个Version的链表。生成新Version并加入到Version Set的流程示意图如下：

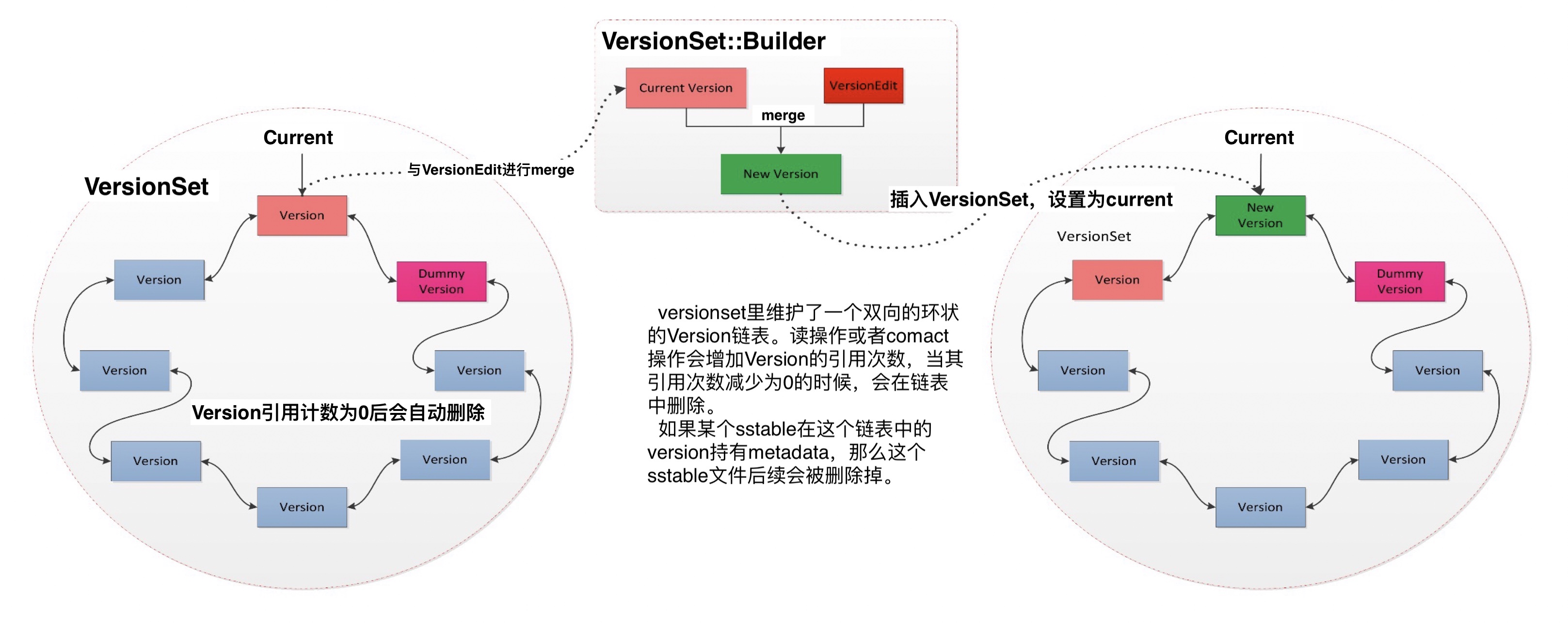
此外，VersionSet需要做一个持久化，因为，如果数据库重新启动或者恢复的时候，没有VersionSet持久化会导致需要将所有的SSTable文件全部遍历一遍，严重降低启动速度。

Minor Compaction 流程

之前我们说过，Minor Conpaction就是当内存中的immutable memtable大小到了一定值的时候，将其保存到SSTable的Level 0中

每次插入操作，都会检查是否memtable超过限制，超过了就会触发函数，进行compaction

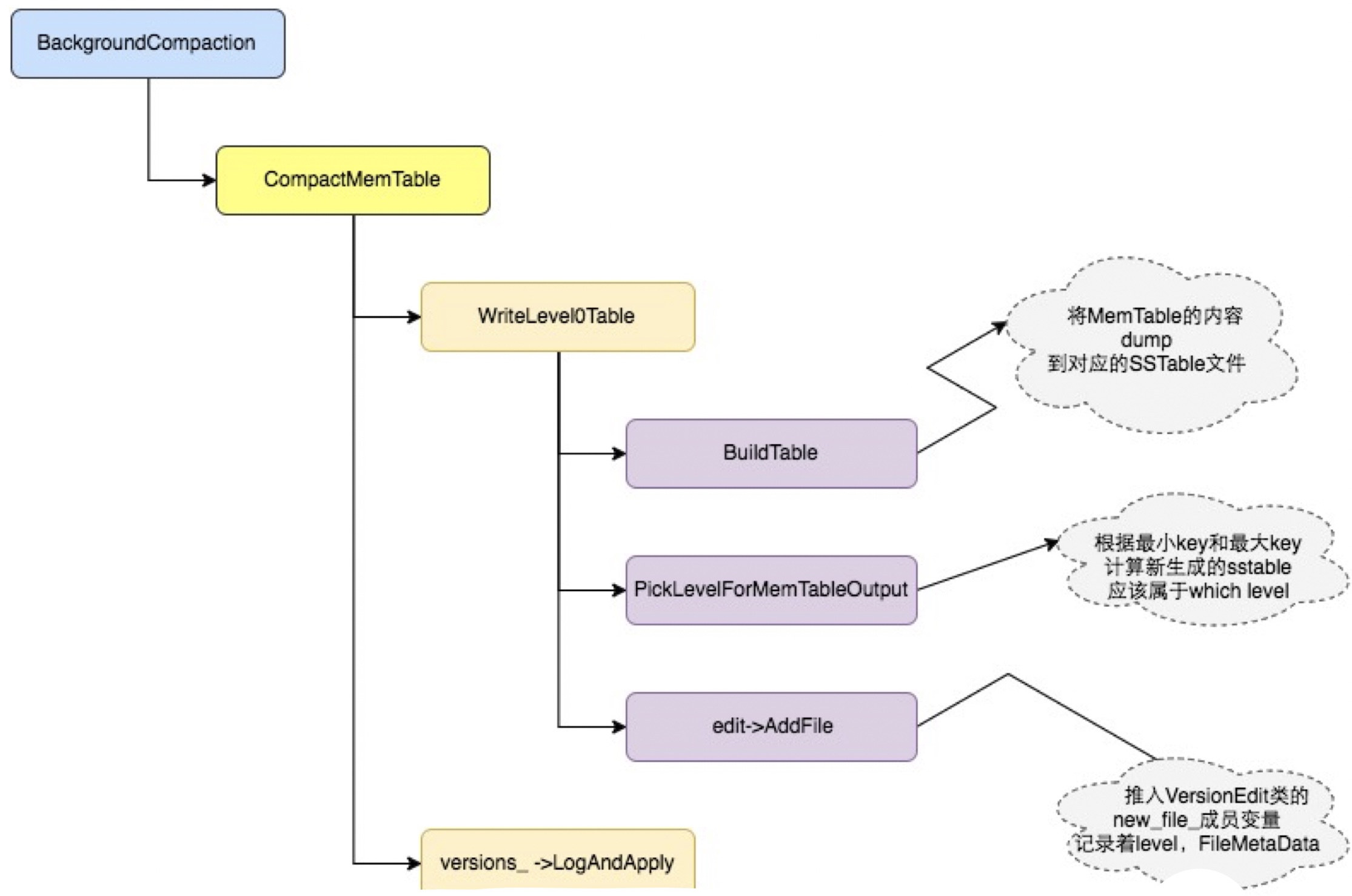
合并流程：

• 构建SSTable
• 寻找合适的Level
• 生成Version Edit
• 应用到当前Version

Major Compaction 流程

大合并的过程就是将Level n层合并成Level n+1层的过程。

首先我们要判定什么时候会触发Major Compaction

• 某个Level的 SSTable太多
• 某个Levl的某个SSTable不成功seek次数太多。

现在开始进行合并，需要确定参与compaction的文件。怎么理解呢？比如说下面这个SSTable，Level1中间的.sst 触发了大合并，和这个文件相关的，是level2中的两个.sst文件，这两个文件和Level1有交集。

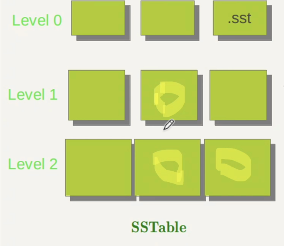
合并文件结束的时候，需要更新Version

并发索引

在数据库中有两处需要并发：1. 上层的事务的并发2. 数据层面的索引并发。这两者是没有关联的。

Concurrent Linklist

我们用的数据结构就是有序列表， 假定有序链表不允许重复元素。

我们要实现3种方法的并发：

• add(x) 增加一个元素
• remove(x) 删除一个元素
• contains(x) 查找一个元素

在链表中，每个节点包括：

• Key
• 一个指向后面节点的指针 next

并发控制的异常

要实现并发控制常常从可能出现的异常出发。常见的异常就是：

• 丢失更新

丢失更新常常发生在两个插入操作之间的，比如下图，6号先插入，但是后来插入的7号把六号给覆盖了，那么此时就发生了丢失更新

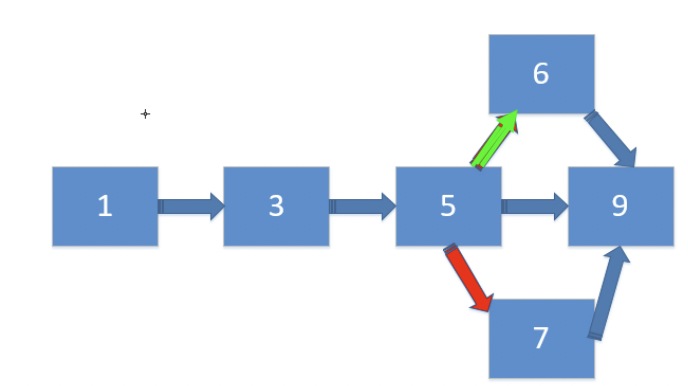
• 假删除

假删除发生在两次remove的时候,如下图，同时删除3和5的情况。

此时对于节点5来说，Prev指针指向3，cur指针指向5；对于节点3来说，Prev指针指向1，cur指针指向5。

如果先删掉5，那么就让 prev->next = cur->next

在并发时删掉3的话，由于此时对于3号节点的cur先于删掉节点5前获得，因此在执行prev->next = cur->next 的时候还是会指向节点5。也就是说5号节点被恢复了。

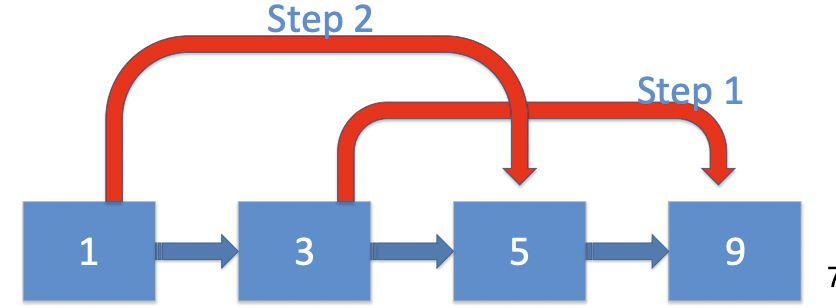
• 插入节点被删除。

  比如我想删除b然后插入c. 但此时，由于b已经删掉了，而c在插入时是连接在b上面的，因此相当于c也被删掉了。

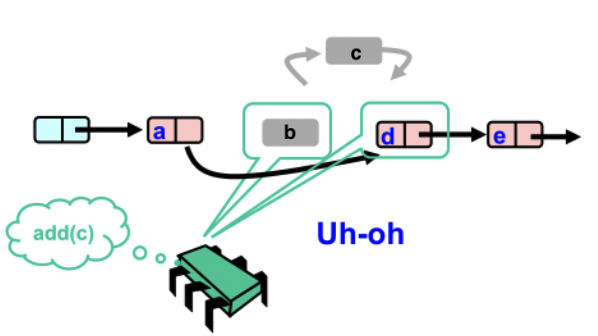
并发控制的方法

寻求并发控制方法就是防止上述异常的发生。通常来说有这么几种方法：

粗粒度锁

粗粒度锁就是对add(), remove(), contains()三个操作 加锁，锁住整个数据结构

• 访问链表时加锁，操作完成后释放锁
• 最安全
• 效率最差

细粒度锁(hand over hand locking 或 lock coupling)

细粒度锁其实这是用一对锁。链表向前推进的过程中，先获取 curr锁，然后再释放prev锁 。数据操作时，同时锁住前驱和后继

head.lock();
pred = head:
try{
		curr = pred.next;
		curr.lock();
		try{
      // 推进过程
      while(curr.key < key){
          pred.unlock();
          pred = curr;
          curr = curr.next;
          curr.lock();
      }
    if(curr.key == key) {
		    return false;
    }
    //插入操作
    NodeWithLock<T> node = new NodeWithLock<T>(item);
    node.next = curr:
    pred.next = node;
    //插入操作停止
    return true;
    }finally{
		    curr.unlock();
		}
}finally{
	pred.unlock();
}

比如说我想在节点8和节点10之间加入节点9。那么首先curr指针会指向节点10，pred节点会指向8。在停止推进时，pred和curr都没有解锁。只有当插入操作停止值之后，才依次放开两个锁

使用了这种细粒度锁，可以避免上述异常的发生，我们以并发删除两个节点为例：

1. 首先，remove(c) 先操作，锁住哨兵节点

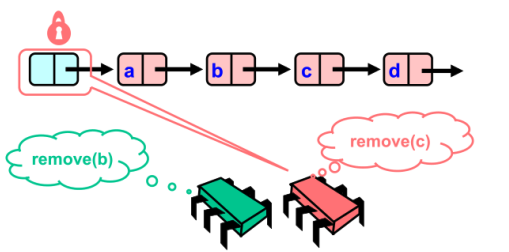
1. remove(c) 向前推进，同时释放前面的锁。这里红色方锁住了b和a。与此同时，remove(b) 代表的绿色方也开始遍历链表。

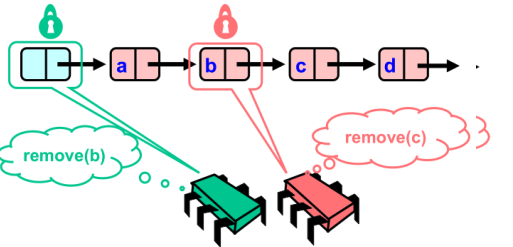
1. 绿色方继续遍历链表，要删除b必须获取b节点上的锁，但是该锁现在在红色方手中。因此绿色方只能等待

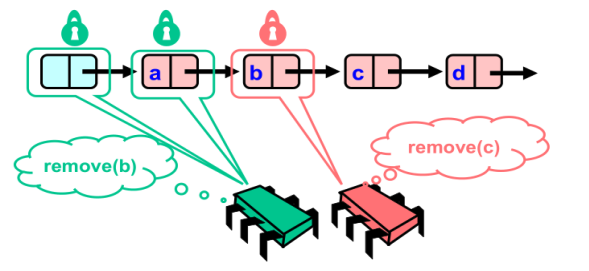
1. 红色方继续遍历链表，获取了b节点和c节点上的锁

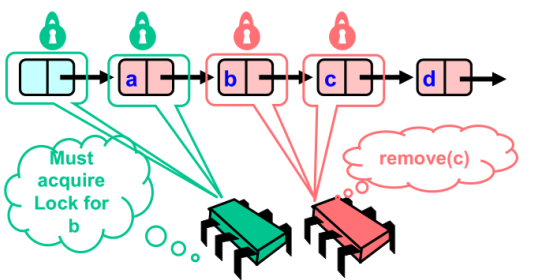
从这里也可以看出，如果只锁住了一个节点是行不通的。加入红方只锁了c，前面b没有锁，那么绿色方就可能获取到b的锁。那么此时红方和绿方的删除操作就可以同时进行了

如果我们只锁了b，那么如果存在另外一个删除操作transact2想要删除d节点，transct2就会锁上C。如果tran2先执行，那么它会让 c->next = d->next 也就是e节点；然后再执行我们的删除c操作：b->next = c->next ,也就是d节点。事实上，最终的结果并不是 b节点指向e节点，而是b指向d，c指向e。

1. 红色方执行删除操作

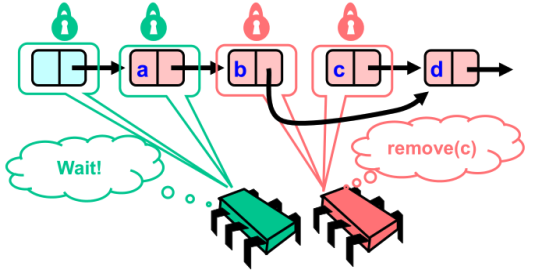
1. 红色方完成删除操作，释放锁，因此绿色方可以继续遍历

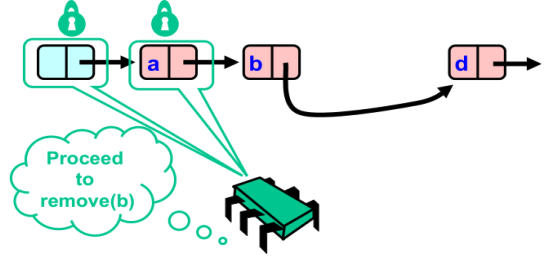
1. 绿色方获得了a和b节点的锁，可执行删除操作

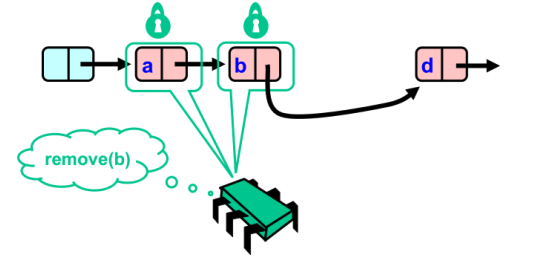
1. 删除完成

   

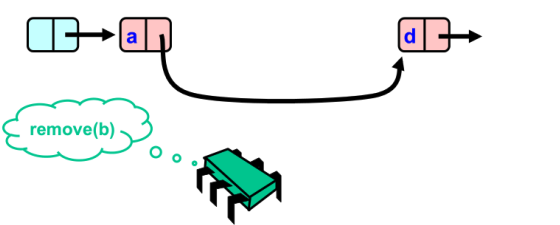
乐观锁

之前的Lock Coupling需要不停的去获得和释放锁

那么我们可不可以这样？只在需要加锁的时候再加锁

1. 只有在寻找到要加锁位置的时候才加锁，之前不加锁
2. 需要加锁时，先加锁，再进行验证是否现场已经被修改
3. 如果验证失败就需要从头开始重试

Lazy List

对于乐观锁，虽然很乐观但还是需要加锁，有可能在验证时失败了需要重试，但是对于Lazy List，它使用标记删除 法

标记删除法的意思就是先做逻辑标记，然后在标记后进行删除。

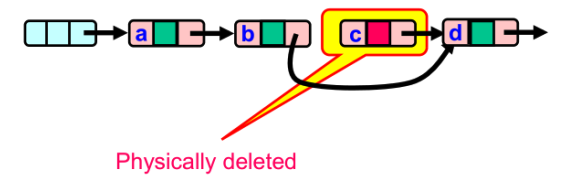
无锁编程

这几种方法并发能力越来越强，但是实现起来复杂度也越来越高

Concurrent Index

现在我们来看看B+树上并发控制的一些技术。

• 正确的读操作：

  • Read Case1: 不会读到一个处于中间状态的键值对：读操作访问中的键值对正在被另一个写操作修改

  • Read Case2: 不会找不到一个存在的键值对：读操作正在访问某个树节点，这个树节点上的键值对同时被另一个写操作（分裂/ 合并操作）移动到另一个树节点，导致读操作没有找到目标 键值对

• 正确的写操作：

  • Write Case1 两个写操作不会同时修改同一个键值对

读和写的第一种情况是常见的读写冲突和写写冲突，如果是单版本存储，那么几乎任何时候都会存在。但是对于读的第二种情况，是B+树特殊的并发控制需求。

场景： 考虑一个读操作刚拿到一个叶子节点的指针，打算访问这个节点后半部分的数据，此时一个写操作发生使 得节点分裂，那么后半部分数据将分裂到另一个节点上， 因此读操作的指针无法获得目标数据。
这时候，简单的对数据加锁无法保证R2的需求。

如下图，P1是一个查找操作，需要找的内容是15；P2是一个插入操作，需要插入9。这两者毫不相关，但是在某些情况下却会造成冲突。

在P1已经拿到了指针，需要读取15的时候，却被P2操作“捷足先登”了，但是因为插入了9号，导致下一层节点发生裂变。这时候原指针指向的区域就没有15了，因为15到可新的孩子节点中去了。

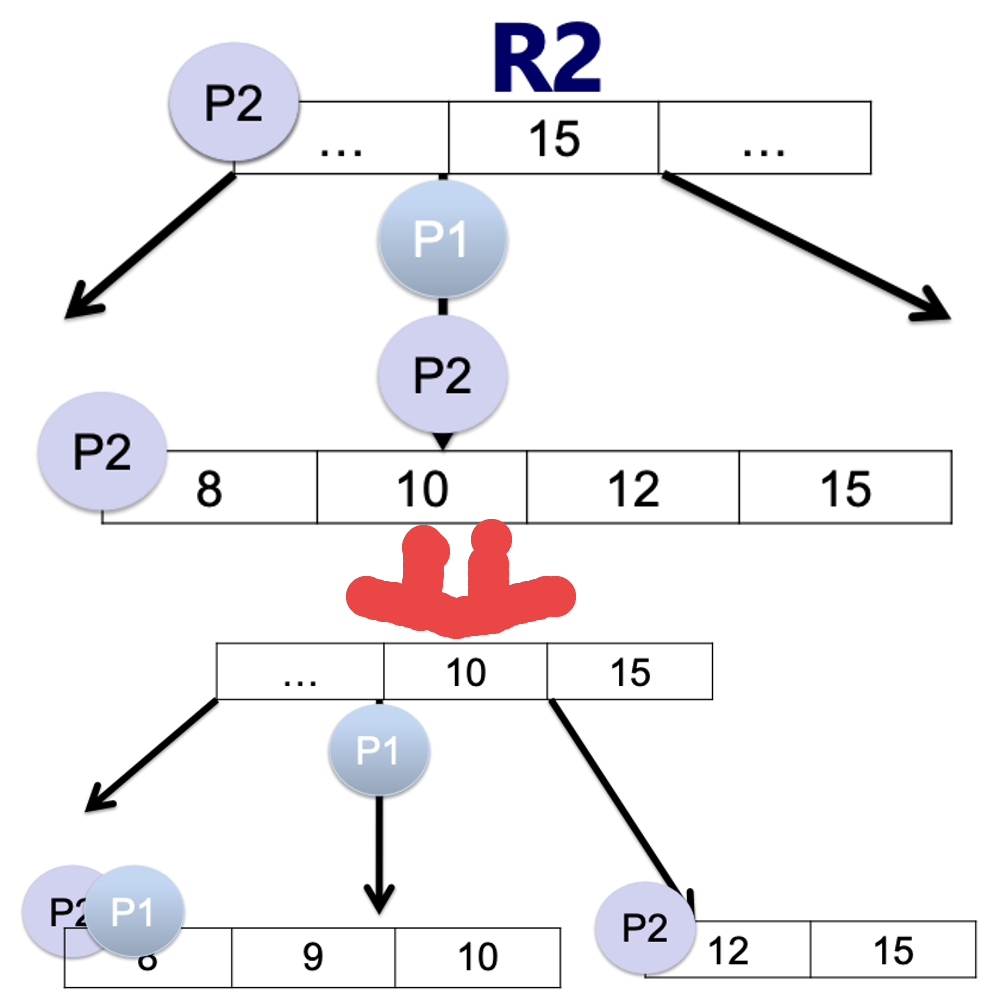
思路和之前的有向链表是类似的。

粗粒度锁：

对于整个索引上锁(对整个B+树数据结构上锁)

细粒度锁

不再对整个索引加锁，使用节点粒度的S/X锁(S锁：共享锁，用于读操作；X锁: 排他锁，用于写操作)

• 写操作

current <= root
XL(current)
While current is not leaf do {
    XL(current->son)
    current <= current->son
    If current is safe do { //如何判断？
        /* Unlocked ancestors on stack. */
        XU(locked ancestors)
    }
 }
 /* Already lock the modified branch. */
 Modify the leaf and upper nodes
 XU(current) and XU(locked ancestors)

其实这个操作和链表中的细粒度锁就很像了，在链表中是前后节点上锁，在B+树中就是对父子节点上锁

• 读操作

/* Algorithm4. 读操作 */
current <= root
SL(current)
While current is not leaf do {
    SL(current->son)
    SU(current)
    current <= current->son
}
Read the leaf node
SU(current)

乐观读

使用一个节点的版本标记判断节点是否更新 – 减少R1带来的读操作带来的锁或latch开销.

B+树乐观读和链表中的乐观读

procedure traverse(root, key){
		node = root;
    while (node is not a leaf){
        t = turn-off-LSB (node.ccinfo);
        next = find next (node, key)
        if (node.ccinfo = t) node = next
  }
		return node ; //判断节点是否被修改过
}

在多核系统下加锁方式效率低

在多核系统下，CPU的性能是主导的，IO性能反而没那么重要. 因为多核情况下每个核有缓存，每次加锁解锁都需要读入内存中去。而且每个核的缓存中的变量需要要求保持一致，因此，会出现 Cache Coherence的问题, 由此导致CPU效率低下。

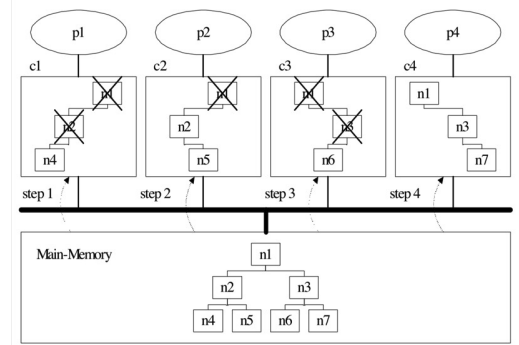
繁加锁操作在多核处理器上会产生Coherence Cache Miss过高的问题。以上图为例， 假设有4个处理器（p1/p2/p3/p4），每个处理器分别有自己的private cache （c1/c2/c3/c4）。假设有4个线程（p1/p2/p3/p4），与处理器一一绑定。下文中的 n1/n2/n3/n4/n5/n6/n7可以指的是树节点的锁，也可以指代树节点。为什么频繁加 锁会引入较高的Coherence Cache Miss开销？

• p1访问树节点n1/n2/n4，然后将它们放在缓存c1；
• p2访问树节点n1/n2/n5，然后将它们放在缓存c2；
• p2修改的S锁会导致缓存c1中的n1/n2失效；
• 注意即使缓存c1中有足够大的空间，这些缓存缺失操作依然会发生；
• p3访问树节点n1/n3/n6，然后导致缓存c2中的n1失效；
• p4访问树节点n1/n3/n7，然后导致缓存c3中的n1/n3失效；

消除R2所带来的加锁-Blink Tree

• 这个Blink Tree和普通B+树不同，在每个节点添加一个 右指针，指向右兄弟节点
• 一旦search的key比节点最高值大，则使用右指针访问右兄弟而不是孩子 ，可以在这一层中查找。
• 假定节点写操作是原子的，那么search操作无需加锁

SkipList上的并发控制问题

我们仅关注插入和查找这两个问题。

首先我们讨论并发操作对数据结构本身的正确 性是否会产生破坏

• 插入/插入操作

  • 丢失更新的问题

• 查找/插入操作

  • 插入一个数据，有没有可能让另一个已经存在数 据读取失败

其次，考虑查找/插入操作的一致性

比如说，在下面这个跳表中，我们插入17，有无可能让19或者12的查找失败？

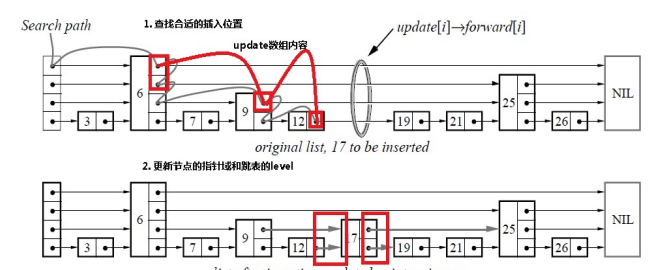
那就要看，新插入的节点的指针，是从下层往上层更新还是从上层往下层更新了。

如果是从上往下更新。那么查找12的时候，还是能找到的。

但是如果需要查找19，此时17的第二层指针已经更新，因此判断出19应该在17-25之间，因此下沉继续查找。但是下层指针还没有更新，那么就找不到19了。

如果从下往上更新，那么12、19都是可以找到的。

我们在来看看插入、查找操作的一致性问题。如果考虑插入17和查找17两者的并发，那么理论上，线性一致性可以原子化，称为时间轴上的一个点，以timestamp的形式存储。

假设插入17的timestamp是A, 查找是B

• 如果A>B , 那么查找17将返回找不到
• 如果A<B, 那么查找17能找到

假定我们定插入/查找的timestamp分配时 间是他们操作开始的时候，是否能做到线性一致？

• 如果A>B, 一定能做到，因为可通过版本号直接判断

• 如果A<B(插入在前)，有可能无法保证，因为实际插入操作可能迟迟没有发生

因此，上述定timestamp的方式无法做到线性一致

其他

SnapShot

我们需要了解SnapShot的概念：即系统在某个时间点的一个全量状态。比如我需要出2011的资产负债表，这需要数据保持在2011年12月31日零点时的状态。

快照,其本质类似于数据库的照片,也就是在某个特定时间点(创建快照的时间点)给数据库拍个照放在那儿.但是这个照片是一个新的数据库,可以应用SQL语句.

快照数据库里的数据是不变的.创建快照后,系统会对原数据库的所有数据页做个标识,如果数据页在创建快照后被修改,会复制一个数据页出来,没有修改的数据页则不会有快照(原数据库和快照数据库共用该数据页).

从这样来看,快照存在的时间越长,对系统的压力会越大(要维护的变化数据页太多).

Memory Allocation

在系统实现的时候还需要考虑分配内存这个重要因素。

数据库里的内存分配和算法题中的内存分配完全不一样，通常会有一个完整的内存管理模块来统一管理内存。这个模块会一次申请大块的内存，多次分给客户，这样可以避免new/delete多次的申请和释放引起的内存碎片。

在一个内存管理模块中，通常需要两个函数：Allocate函数和AllocateAligned函数

• Allocate函数

如下所示，管理器会先申请一大块内存，默认每次申请的大小为4KB，同时记录下剩余指针和剩余内存字节数量。这样可以让申请到的内存在一个连续的空间里面。

然后，每当有函数向管理器发送申请，如果当前剩余的字节能满足需要，则直接返回给用户；如果不能，对于超过1KB的请求，直接new返回(左边第二个红块)，小于1KB的请求，管理器则会向内存申请一个新的4KB块并从中分配一部分给用户。

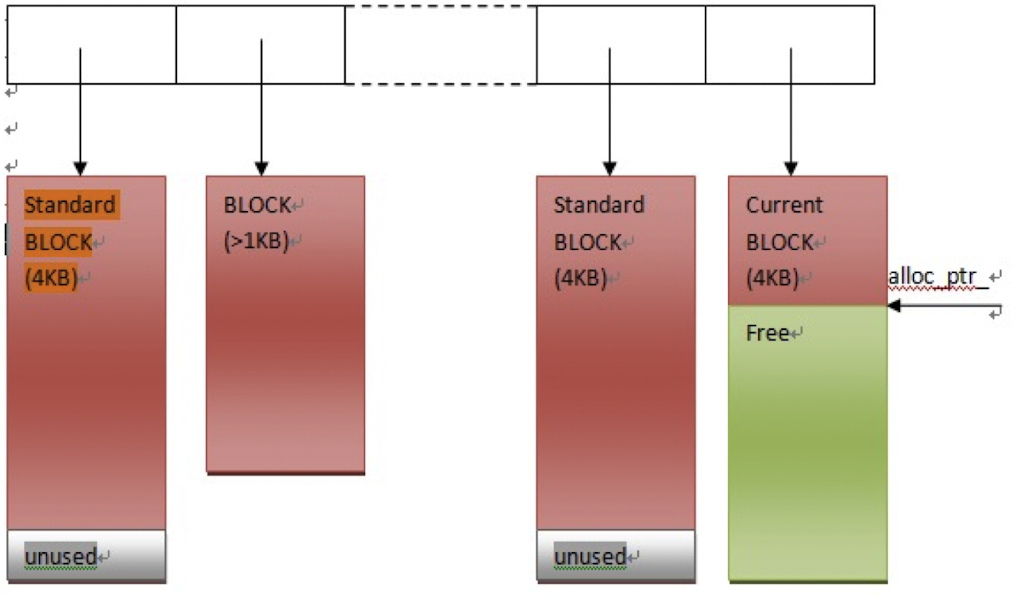
• AllocateAligned函数

这个函数的作用就是做到地址对齐，让内存首地址是4或者8的倍数

Bloomfilter

可参考这篇文章： 数据科学与工程算法-哈希：布隆过滤器

Second Index

什么是二级索引？二级索引就是定义在非主键上的索引，这在数据库中有很广泛的应用。

二级索引的作用是什么？为非主键提供数据访问的有效路径

二级索引的几种选择：可以是B+树，Block Index等

其实有一种更简单的方式：把二级索引看做是一张特殊的表——索引表

• 比如说有数据表<主键，非主键列1，非主键列2，非主键列3>, 我们要在非主键列1上构建二级索引。我们就可以建一张索引表：<非主键列1(作为主键)，主键列(作为 非主键)>。这样，非主键列1自动就会有索引效果了。
• 当我们要查找非主键列的时候，先查询索引表，然后依靠索引表上的主键去找到主键列对应的数据，再根据主键列的值去原本的数据表中查找。

回表查询VS非回表查询

• 非回表查询：只查询索引表就能得到想要的结果。比如说只查找非主键列1
• 回表查询：需要通过索引表再返回数据表查询才能得到查询结果。比如说根据非主键列1去找到非主键列2

二级索引的更新

• 同步更新
  • 在主表更新时一起更新
• 异步更新
  • 在主表更新之后，查询之前更新索引表

这就引入了一致性问题，通常大多数数据库都是采用同步更新的方式。因此索引越多，数据库写入的速度也就会越慢

压缩

压缩在数据库中是很常见的技术。可以参考博客：Compression

压缩可以通过两种主要方式实现：

• 无损：可以从压缩数据中完全重建原始数据。
• 有损：由于故意降低质量而减小数据

我们用几个问题来学习一下数据库中的压缩技术

数据库压缩有什么好处?

大多数压缩算法都会构建一个内部编码字典来管理压缩关键字。当数据库大小较小时，由于创建了额外的字典，压缩文件可能比未压缩文件大。

对于任何数据库，压缩和解压缩都是高于其常规 DML/DDL 操作的任务开销，它消耗额外的 CPU/内存。所以必须是只有当优化页面读取所带来的CPU/内存收益远远大于压缩开销时，才可以尝试压缩。

虽然压缩可能作为后台任务并行发生，但解压缩会引入客户端延迟，因为它在客户端查询后会在前端进行解压缩。但是，像 Oracle 这样的商业数据库支持高级压缩技术，无需解压缩即可读取数据库。

数据基数较差时不推荐压缩。对于数字数据和非重复字符串，不要压缩数据。对于数据BLOB（图像、音频）等数据类型，根据压缩算法，存储大小可以减少或增加。

总之，在实时数据库上实施之前，估计任何算法可能的存储和性能优势非常重要。

压缩对常见数据类型有什么影响?

压缩是一种 DDL 功能，可以使用CREATE,ALTER和BACKUP命令选择性地应用于表、索引或分区。

数据压缩适用于这些数据库对象——堆、聚集索引、非聚集索引、分区、索引视图。

行级压缩将固定长度数据类型转换为可变长度类型。因此，这适用于固定长度的文本和数字字段 ( char, int, float)。

• 例如，将 23 存储在一int列中，压缩时只需要 1 个字节，而不是分配的全部 4 个字节。
• char(100) 也不会占用100个字符空间
• NULL 或 0 值不占用空间。

有哪些流行的数据库压缩技术?

数据库通常避免在后端进行有损压缩。在无损技术中，所有压缩数据都以二进制形式存储。

• Run-Length Encoding。在这种技术中，会扫描顺序数据以查找重复符号，例如图像中的像素，并用称为“运行”的短代码替换。比如说，对于灰度图像， run-length code 可以表示为 ${S_i,C_i}$,其中Si是像素的符号或强度，Ci是 的计数或重复次数Si。
• Prefix Encoding。之前我们在SSTable中介绍过这种方式，是另一种仅适用于同类数据的基本技术。数据字段的第一部分匹配通用性，而不是整个字段。因此我们将相同的前缀存储起来，做为编码。
• Dictionary compression。字典压缩是另一种应用于页面的压缩技术。该算法计算对列的单个属性进行编码所需的位数 (X)，然后会计算这X位中有多少可以放入1、2、3、4个字节中，进行压缩。

数据库压缩与通用数据压缩技术有何不同?

通用数据压缩可以使用于字段，比如说，将单个数据项占用的空间最小化；但是，数据库中的压缩方法是一种aggregate technique(聚合技术) ，它是将跨行、跨列、跨页面的数据进行压缩。

除了在数据库级别应用压缩外，在字段级别应用数据压缩也很常见：

• 对于图像压缩，可以使用BMP到JPG的有损压缩。
• 又如可以用无损方法在DB级别压缩BLOB数据字段。
• 虽然NULL值无法单独进一步压缩，但是当DB中出现一系列NULL值时，Sparse Column等压缩技术可以共同优化NULL的存储

数据库压缩技术不仅压缩实际数据，它们还作用于派生实体，如索引、视图、集群和堆。但是，对于索引等派生实体，在索引查找或扫描期间重建键列值的 CPU 开销很小。这可以通过在块中本地保留前缀来最小化。

关系数据库和分层数据库的压缩技术

应用于关系数据库和Level DB的压缩算法没有很大的区别，只是命名方式有所不同。

Level DB 具有类似于 RDBMS 中的表的段。段中的字段与列进行比较。

但是，在分层数据库中，段之间是隐式连接的。因此，I/O 分页过程会有所不同，因此算法必须考虑页面大小。

大型软件应用程序如何处理数据库压缩?

• Facebook 使用具有超快速解码器的实时压缩算法Zstandard以及用于小数据的字典压缩。
• Google 在其 BigTable 和 MapReduce 系统中使用Snappy，这是一种高速压缩算法。
• 像SQL Server这样的商业 DBMS使用行、列和页面级别的压缩。SQL Server 使用专有的XPRESS算法进行备份压缩。
• Oracle 使用称为Oracle Advanced Compression的内部压缩技术。
• 开源 MySQL 使用LZ77算法进行 InnoDB 表压缩。

Design Consideration

• Should be aware of the storage hierarchy

对存储的层次结构(CPU缓存，内存，磁盘)要有很深刻的概念。因为数据库是数据密集型的应用，而不是计算密集型的应用。如何提高IO性能是我们要研究的方向。

1. Database is usually data-intensive
2. cache miss is important 缓存命中率是很重要的

• Pay attention to the hardware properties

1. Sequential access and random access is usually different
2. bandwith and IOPS

• Design Issues 设计时的问题

1. choose a proper index
2. support variable length data
3. for most secondary storage, try avoid random writes
4. reduce the write amplication
5. group your writes

• Optimization On LSM-tree 优化LSMT的性能

1. optimize write amplication
2. optimize read performance
3. other optimizations: cache, special workload

总结