AI-Searching

Searching

搜索的方法有很多种，但是大体上可以分为两个大类——盲搜和有先验知识的搜索

Uninformed Search Methods

Depth-First Search

Breadth-First Search

Interative Deepening

Uniform-Cost Search

对于深搜和广搜我们都已经十分了解了，现在我们来学习另外一种搜索方式——代价一致性搜索，即Uniform-Cost Search(UCS). 其示意图如下：

首先，如果要使用UCS进行搜索，我们需要先定义一个 $g(n)$, 它代表了根到第n个节点的代价。UCS的代价就是，每次选择$g(n)$最小的节点进行展开，不管它它的目标状态有有多远。因此，UCS

算法流程

(1）将起始点加入到frontier中，将与frontier相连的点进行探索，每个点的代价（后面用cost替代）是从起点到该点的距离，然后将所有的点加入到frontier里面

(2) 从frontier里面挑出cost最小的点A，判断该点是不是终点，如果是终点算法结束。如果不是终点，探索与该点相连的所有点，每个点的cost是A点的cost加上A点到B点的路径的权重。如果B点是已经出现在frontier里面了，比较一下原来的cost与新生成的cost哪个更小，然后将最小的cost赋值给B点，并更新它的父节点。

(3) 如果frontier为空还没有找到终点，则没有到达终点的最短路径

例子

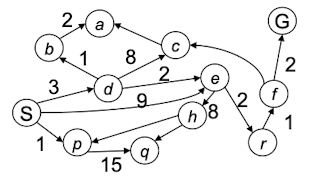
对于上面这张图，我们对其进行UCS搜索，找到S到G的最短路径。

1. 首先，S的邻接节点是d、e、p，他们的$g(n)$分别为： $g(d)=3,g(e)=9,g(p)=1$
2. 我们选择$g(n)$最小的节点p，并把p的邻接节点q加入到队列。现在的队列为：$g(d)=3,g(e)=9,g(q)=16$
3. 选择$g(n)$最小的节点d，并把d的邻接节点b、c、e加入到队列。现在的队列为：$g(b)=4,g(c)=11,g(e)=5,g(q)=16$
4. 选择$g(n)$最小的节点b，并把b的邻接节点a加入队列。现在的队列为：$g(a)=6,g(c)=11,g(e)=5,g(q)=16$
5. 选择$g(n)$最小的节点e，并把e的邻接节点h、r 加入队列。现在的队列为：$g(a)=6,g(r)=7,g(c)=11,g(h)=13,g(q)=16$
6. 选择$g(n)$最小的节点a,但a没有邻接节点。因此选择次小节点r，并把r的邻接节点f加入队列。现在的队列为：$g(f)=8,g(c)=11,g(h)=13,g(q)=16$
7. 选择$g(n)$最小的节点f,把f的邻接节点加入队列。现在队列为$g(G)=10,g(c)=11,g(h)=13,g(q)=16$
8. 找到了$S$ 到 $G$ 的道路

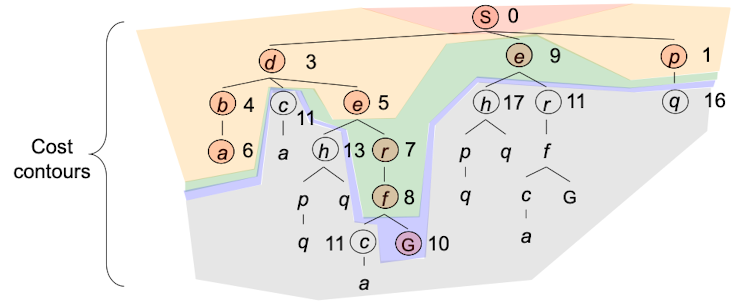
整个过程如上图所示。

算法分析

既然UCS算法是根据当前节点的$g(n)$去进行搜索的，那么就需要一个数据结构来帮助我们存储这些节点的代价。这里我们选择的就是Priority Queue(优先级队列)

由于我们的策略是选择优先队列中代价最小的节点，那么假设目标节点的代价为C*,每次搜索一条边的平均代价为$\varepsilon$.那么UCS的搜索深度就是 $C^*/\varepsilon$ .

由BFS的空间和空间复杂度为$O(b^s)$可推得，UCS要找到目标节点的时间复杂度为: $O(b^{C^/\varepsilon})$ ，空间复杂度也为$O(b^{C^/\varepsilon})$

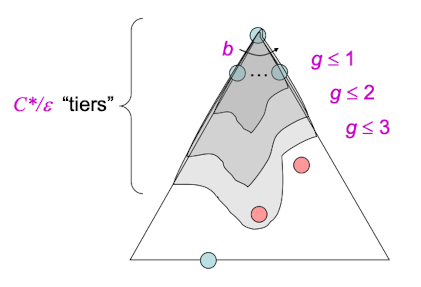
那么UCS是complete的吗?（能够找到最优解)

• 如果$C^*$ 是有限且$\varepsilon>0$的话, 那么UCS是可以找到最优解的

那么UCS是optimal的吗?（能够以最小的代价找到最优解)

• 是的，我们将在接下来的$A^*$Search中对其证明

Informed Search Methods

和之前的盲搜不同，Informed Search Methods是有一些先验知识的搜索方式。在这里我们主要介绍3种方式：启发式搜索、贪心搜索和A*搜索。

什么是启发(Heuristics)

启发，是一个估计某一状态距离目标状态有多近的函数(不一定完全准确)， 它为特定的搜索问题而设计，无法保证最优性。

我们举一个例子：翻煎饼问题。现在有大小不同的四张煎饼，它们以一种混乱的方式排列，我们的目标是将其从小到大排列好。其中，完成目标的代价是每次翻的时候翻了多少煎饼。比如说初始的状态如下所示：

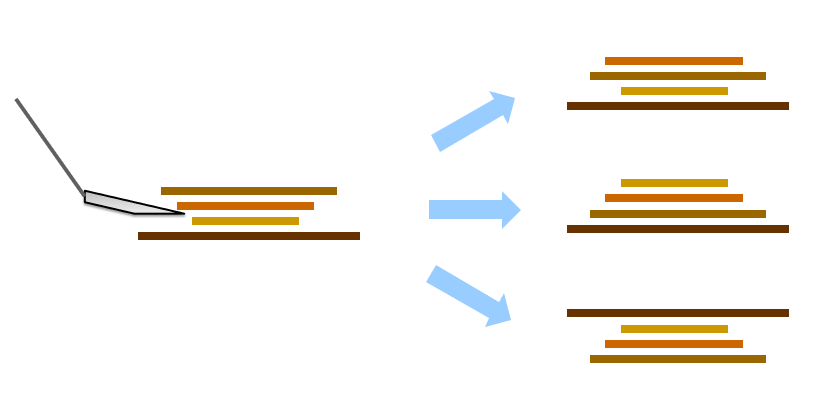
从初始状态可以一步到位变成最终状态，只需要反动三张煎饼即可。

下图展示了在四张煎饼的情况下，各个状态互相转变所需要的代价：

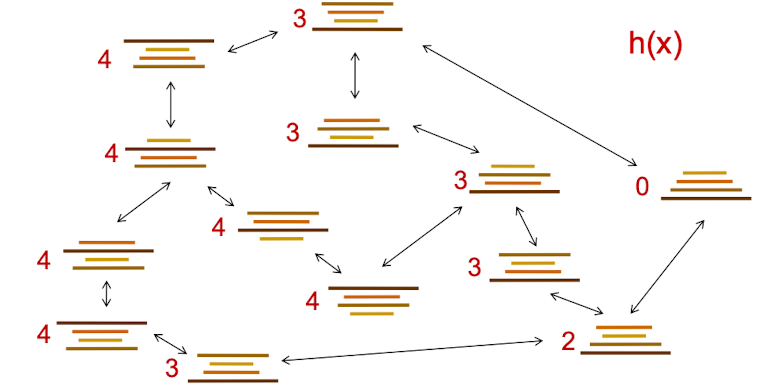
要找出某个状态到最终状态需花费的最小代价，可以用UCS，但是更好的方法是：告诉电脑以当前状态有多少煎饼不在正确的位置作为启发，并进行搜索。

• 又比如，对于pacman小游戏来说，我要让吃豆人以最优的方法到达目标位置，可以告诉电脑当前吃豆人距离目标点的欧几里得距离或者是曼哈顿距离。

• 再比如，对于罗马尼亚旅行问题，我们可以以任意两个城市之间的直线距离作为启发。

  

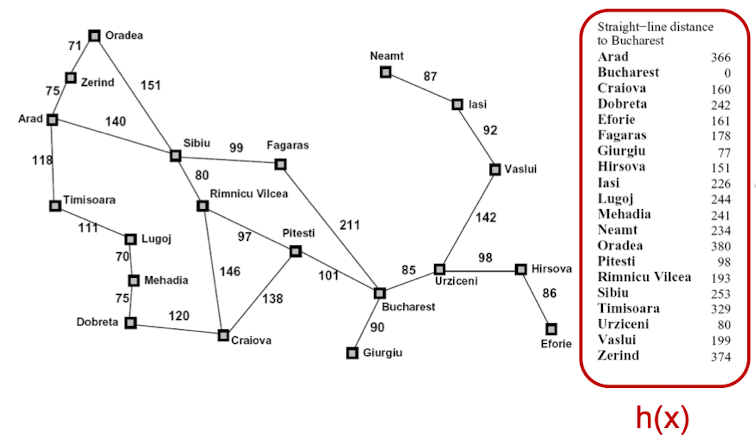
Greedy Search

贪心就是一种启发式搜索，但是某些基于贪心的启发式可能会退化成dfs（如果这种贪心完全没有起效果，就等同于在dfs中任意选择下一个节点展开）

启发式的搜索展开节点时，选择可能离目标状态“最近”的节点展开。（例如旅行问题中，展开直线距离离目标节点最小的节点）

贪心法可能让我们获得一个比较好的解，但是无法保证获得的结果一定是最优的。如下图：机器人朝着一颗钻石挖去，挖到了，但是却忽视了更大的两颗钻石

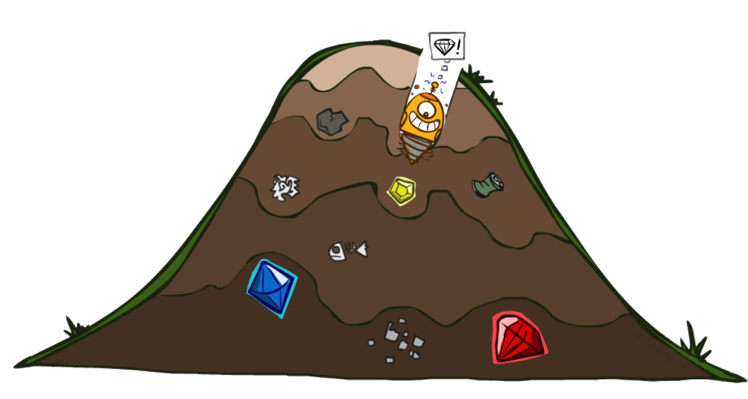
A* Search

A 算法是UCS和贪心算法两者的结合。我们以龟兔赛跑为例，UCS是乌龟、贪心是兔子，结合两者的优点是A 算法。

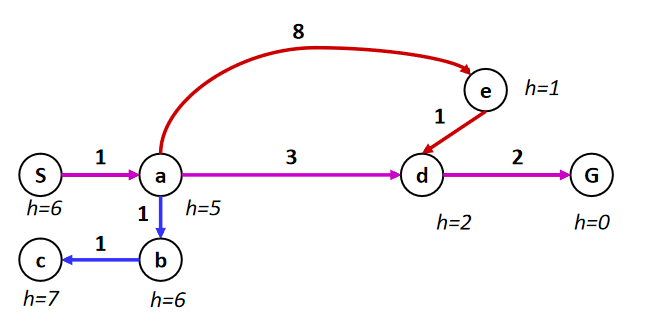
比如说对于上面这张图，每条边都有权重。我们的目标就是，从S出发，找到一条到G的最佳路线。用树来表示，如下

• 如果采用UCS：每次展开的是当前已花费代价最小的节点，即回首过去

  • 从s出发，首先展开a， 现在$g(b)=2,g(e)=9,g(d)=4$
  • 展开$b$,现在$g(c)=3,g(d)=4,g(e)=9$
  • 展开$c$, 发现没路了，而且没到终点，现在$g(d)=4,g(e)=9$
  • 展开$d$,$g(g) = 6,g(e)=9$
  • 展开$g$ ,到达终点

  路线为：$s\rightarrow a\rightarrow b\rightarrow c \rightarrow d\rightarrow g$ , 虽然找到了最有线路，但是绕了一个弯

• 如果采用贪心法：每次展开启发函数最小的节点，即展望未来。

  • 从s出发，首先展开a，$h(e)=1,h(d)=2,h(b)=6$ ，注意，这里的$h(e)=1$ 是通过某种启发算出来的，这里只是举个例子。
  • 展开$e$，$h(d)=2,h(b)=6$
  • 展开$d$, $h(g)=0,h(b)=6$
  • 展开$g$, 到达终点

  路线为：$s\rightarrow a \rightarrow e \rightarrow d \rightarrow g$ ， 找错了线路

• 而使用A*算法，结合了ucs和greedy的优点，即回首过去+展望回来。令函数 $f(n) = g(n)+h(n)$ ,A* 算法中维护一个优先队列，按照$f(n)$ 的值从小到大进行维护。

• 从s出发，首先展开a，$,f(d)=4+2=6,f(b)=2+6 = 8,f(e) = 1+9=10$
• 展开d，$f(g) = 6,f(b)=8,f(e)=10$

• 展开g

  路线为：$s\rightarrow a\rightarrow d\rightarrow g$, 找到了最佳线路，而且花费的时间也最短。

A*算法何时终止？

第一次遇见目标节点（遇见，就是指展开了目标节点的父节点，将目标节点加入队列）时不能退出（此时不一定最优）。只有把一个目标节点剔除队列的时候，才会让算法终止。

记忆： enqueue不止，dequeue才止

• 从S出发，$f(B)=1+2=3, f(A) = 2+2=4$

• 展开B，如果之后选择G节点展开，但是s-b-g的代价比s-a-g的代价要大，所以不能退出

• 因为此时$f(A)< f(G)$，所以这个时候展开A
• 然后从A到G，找到最优的路线
• 将G从队列中移除，停止算法

A*算法的最优性

现在我们来讨论A*算法是不是最优的？

要考虑这个问题，首先我们要想，A*算法是不是始终是正确的？一个很朴素的想法就是，如果我们的启发函数错误地估计了节点到目标节点的距离(比真实值大了很多)，那么这时候A*算法肯定不会选择这个节点作为下个展开的节点。

这时候，我们要设定能使A*算法最优的一个前提：Admissible Heuristics（容许的启发）

$$0\le h\le h^*(n)$$

即启发式算法的估价应该在0和真实代价之间。如果h(n)大于真实代价，则可能找不到最优解，不能保证最优性。

证明

在满足Admissible Heuristics时，A*搜索算法的最优性是可以被证明的：

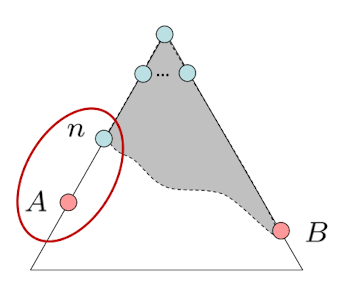
假设：

• A是最优目标节点 optimal goal node
• B是次优目标节点 suboptimal goal node
• h is admissible，估值满足$0\le h\le h^*(n)$

证明思路

• A会在B之前被弹出（fringe）
• 假设A的祖先n（n可以是A本身）、B，都在待展开的队列边缘（on the fringe），证明n会在B之前被展开

证明过程：

• 首先：我们要证明 $f(n)\leq f(A)$ 。 可以从定义入手：
  • $f(n)=g(n)+h(n)$
  • $g(A) = g(n)+h*(n)$
  • $f(A)=g(A)+0 $ (因为$h(A) = 0$)
  • 根据假设 $h(n)\leq h*(n)$ 可知， $f(n)\leq f(A)$
• 然后，我们要证明 $f(A)\leq f(B)$
  • $g(A)<g(B)$ A是最优解，B是次优解。
  • $f(A)<f(B)$ 因为对于AB来说 ，$h(A)=h(B)=0$

因此，所有A的祖先(包括A自己) 都会在B之前被展开。这可以证明，当任意目标节点被dequeue时，最优路径已经被找到了。

关于证明的细节：为什么不仅要证明A会在B之前被展开，还要证明A的祖先也会在B之前被展开？因为证明的假设是A和B都要在队列边缘（A和B都已经被遇见）。我们想证明的是，当B在队列边缘时，总有一个A或A的祖先也在队列边缘，并比B拥有更高的展开优先级。

如果只证明A自身，那么当B在队列边缘时A也在队列边缘这一前提是无法被保证的。

因此我们证明A或A的祖先在队列边缘的情况，应为这能保证在B弹出之前至少会有A或者A的祖先(甚至是根)在队列边缘

A*和UCS的比较

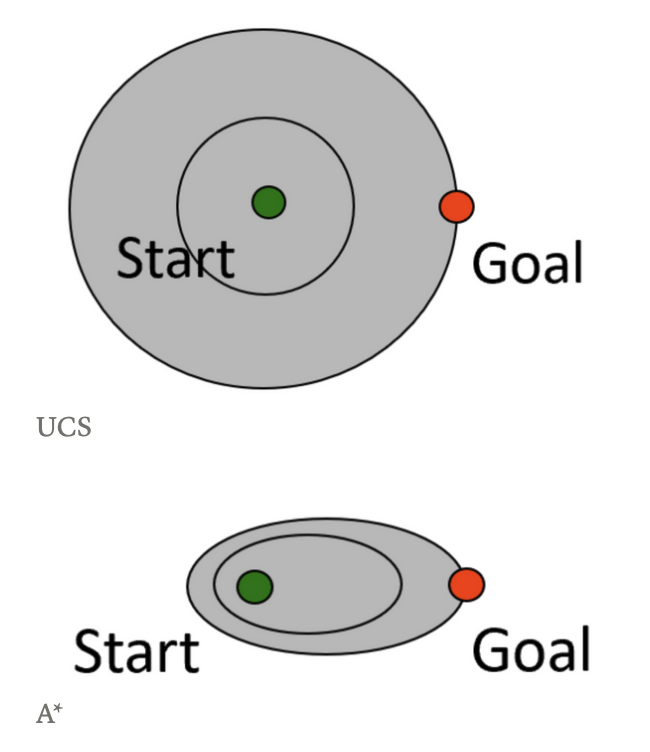
然后我们来看一下在树形状态下，UCS和A*算法的比较。

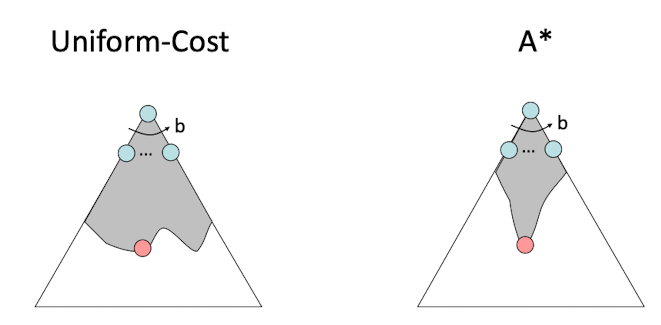
最后我们看一下pacman游戏中，三种不同算法的查询过程比较：

感性理解：A*算法避免了很多没有必要的搜索，A*算法是一种“对冲”，即基于启发式估计h对UCS算法进行“瘦身”。称之为“对冲”是因为启发式估计本身是不确定的，相信这个估计本身就是存在风险的。

怎么设计Heuristic

原始问题通过松弛 relax 来进行处理。例如把整数解问题转换成实数解问题。

设计heuristic的时候也可以先对原问题进行简单的松弛，例如：

• 在旅行问题中，直接使用两点间距离
• 在迷宫问题中，不考虑阻隔，直接使用曼哈顿距离

是否必须admissible

admissible：估值小于等于真实代价

但如果估值比真实代价小太多，也不好。

如果admissible不满足呢？考虑真实代价为9，估值为0.01和估值为10两种情况。

即使10不是admissible的，但起到的效果更好。

具体案例

迷宫问题中的Heuristic

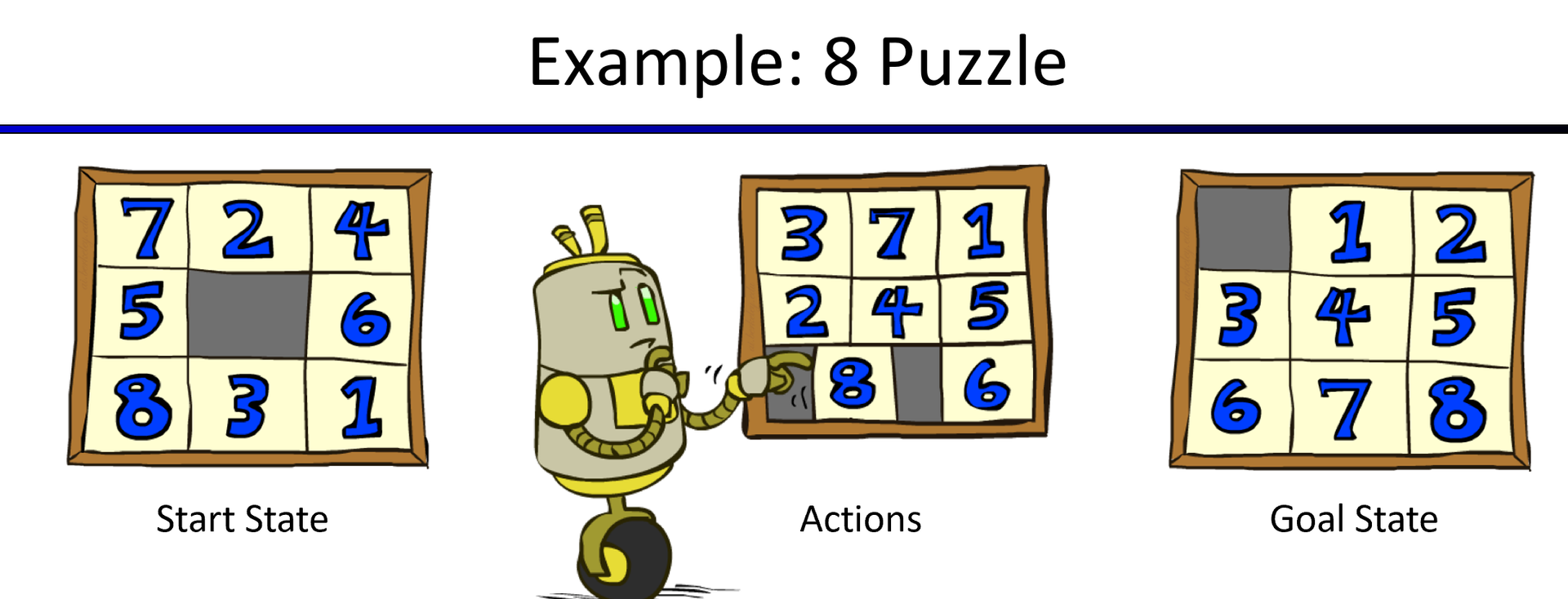
对于如何设计启发函数，我们可以提出这几个问题：

• 状态是什么：可以当做由1-9九个数构成的向量（把灰色格子也看成一个数，比如9）。但是要考虑到每个数的位置，每个数只出现一次。
• 状态数有多少: 整个状态数是 $9!$
• 行为是什么：将一个数移动到相邻的灰色格子
• 后继状态有多少：
  • 灰色格子在角落：2
  • 灰色在边界上但不在角落：3
  • 灰色格子在中间：4
• 真实cost：隔板的真实移动次数。

我们并不知道真实值是多少，但我们可以用松弛的方法去进行估计。下面介绍了两种启发式 ，每周都是admissible的，因为估计的值小于真实值。

松弛1：想象直接把板子拆下来，再直接放到正确的位置上面，一共需要几次，也就是看有多少个隔板被错误放置。我们可以想象，这种方法是将原本需要多步移动的实际情况压缩成一步到位的估计情况。

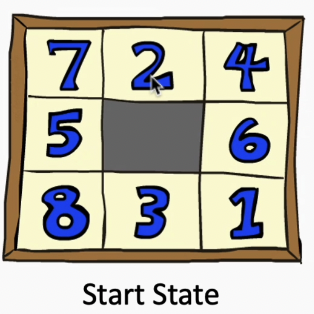
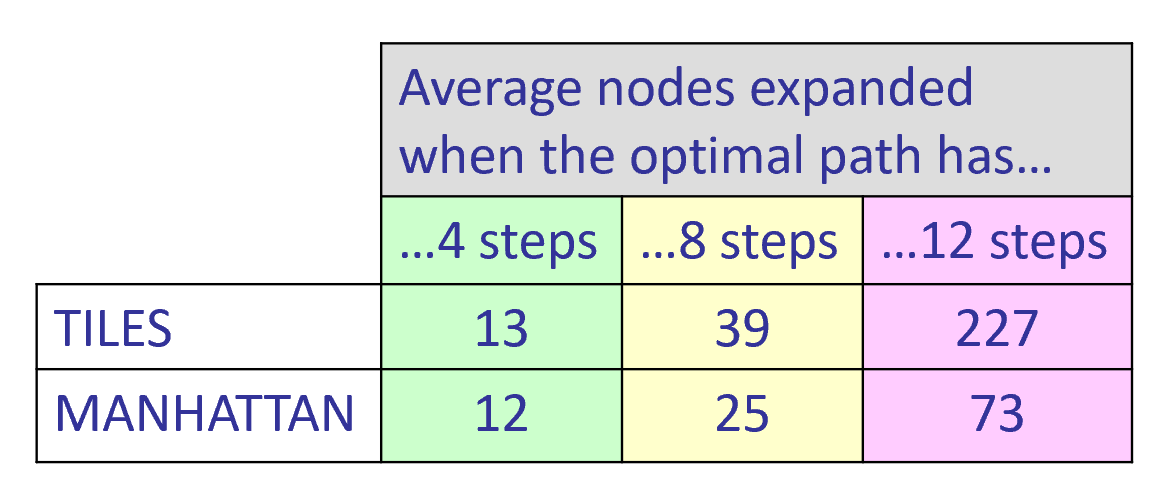
我们观察下面这个表格，在同样移动4步的情况下，UCS需要展开112个节点，而用TILES启发只需要展开13个节点。这种启发式估计相较于UCS展开的节点数明显减少了。

松弛2：不考虑其他隔板的影响（也就是假设移动的时候不会被挡住），基于曼哈顿距离。这种松弛比第一种松弛效果更好了，因为这是一个更接近真实值的松弛。因为用曼哈顿距离估计得到的步数肯定要大于等于1步.

如下图，要把1移到它正确的位置，用曼哈顿距离作为启发的话，是3步，而实际上，肯定不止3步。因为先要移动6这个阻挡块。

最理想的状态是把真实代价作为启发，但问题是不知道真实代价。

对冲（hedge）：A*需要平衡【计算估计】和【展开节点】之间的代价，需要做一个平衡。

Semi-Lattice of Heuristics

现在我们要学习启发式函数的半格特点

启发式函数所满足的特点：

• 支配性Dominance：如果
• Trivial heuristics：有一些状态的估计值是显然的。例如，目标节点的估计值就是0。
• semi-lattice半格原理：$h(n)=\max(h_a(n),h_b(n))$，取max后依然admissible

我们用一个例子来说明一下这个半格原理：

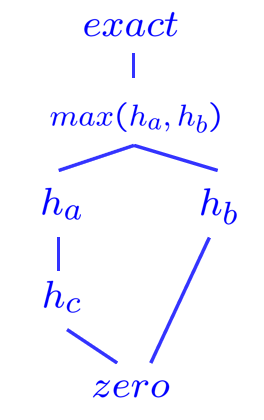
比如说，我现在设计了三个admissible的启发式函数$h(a),h(b),h(c)$ ，且 $h_a$ 是 Dominance $h_c$的，那么在这个情况下我们取一个新的启发式函数，即对于每个节点n，都取 $h(n) = \max(h_a(n),h_b(n))$ . 在这种情况下，$h(n)$ 依然是admissible的

Tree Search 和 Graph Search 对比

Tree search缺点：遇到有环的状态图时，会有重复展开的情况（不知道怎么规避已经展开过的节点）。如下图，我们看到e、a、p、q都是重复访问的节点。

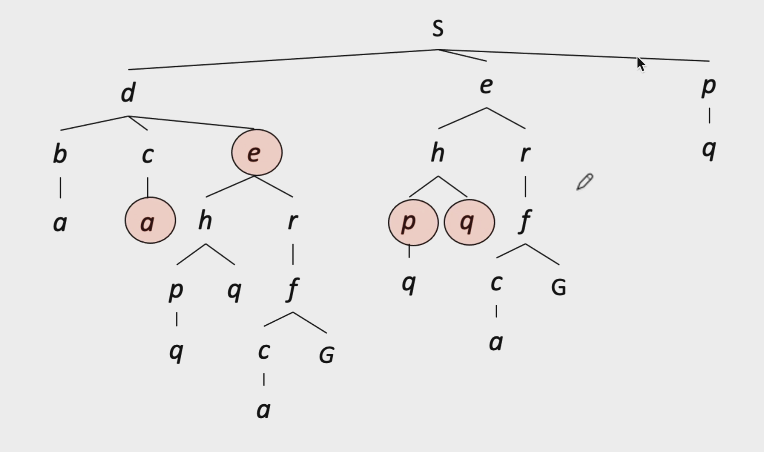
Graph search：不会展开同一个节点两次

• 实现：tree search + 状态集合（记录已展开节点的集合）

  • 用集合记录是为了O(1)查询是否被展开过。使用列表的话，会额外增加搜寻所需要的时间。

• A*用Graph search来做检索会有什么问题？

  重复状态不再展开。因此这时候就出问题了，如下图：

  

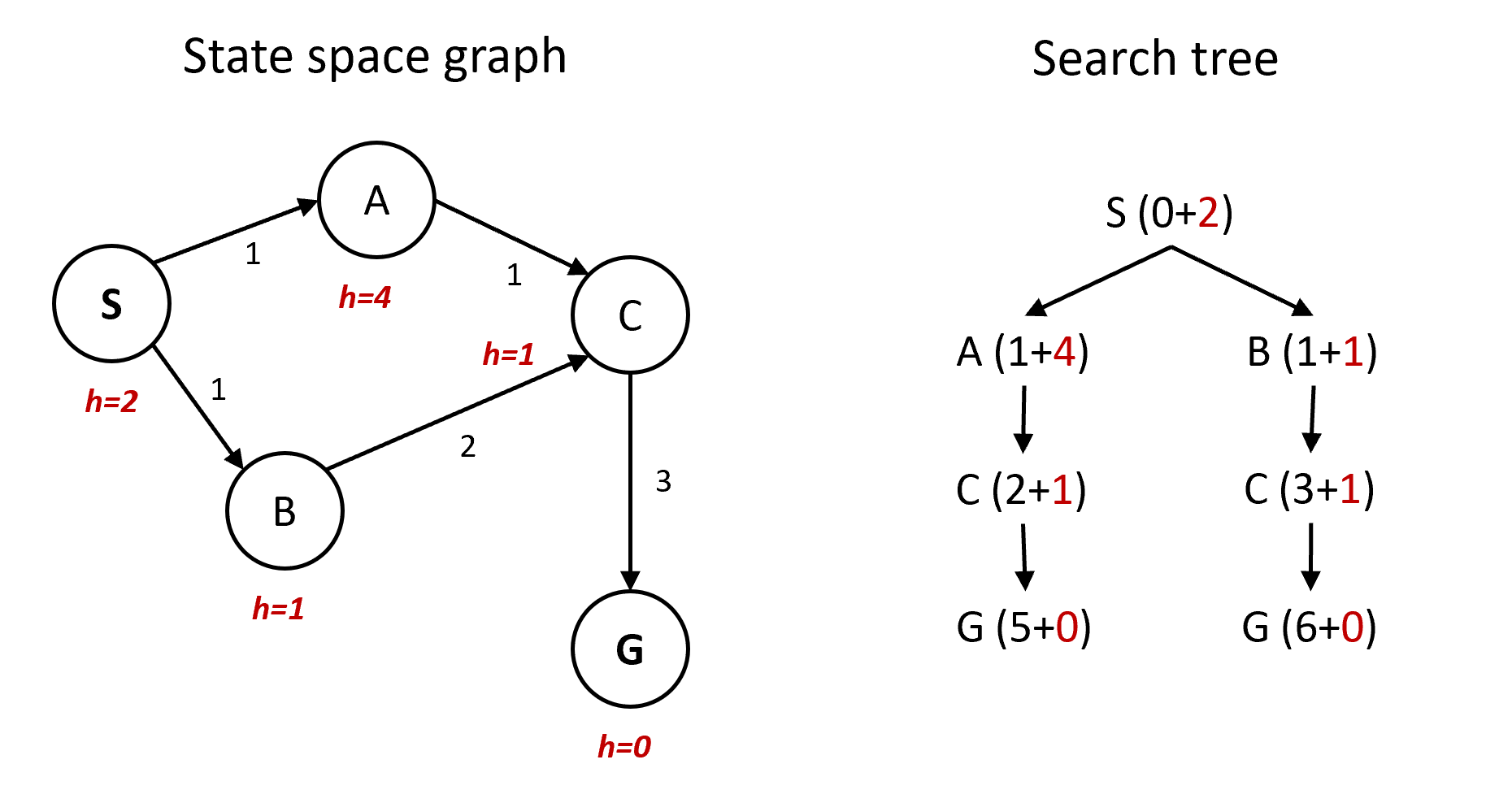
  1. 因为$f(B) = 1+1=2<f(A)=1+4$, 所以先展开 B
  2. B后面只有一个节点C，所以展开C，此时总体代价为3
  3. C后面只有一个节点G，所以展开G，此时总体代价为6
  4. 第一次访问 G(6+0) 时，由于已经访问过一次，所以 G 就不会再被展开。
  5. 然后发现，$f(a) = 1+4<f(G)=6+0$ ，且A未被展开过，因此访问A
  6. A后面有一个节点C，且$f(C) = 2+1<f(G)$ ，因此展开C
  7. 现在C后面是G，但是G已经被访问过了，因此A* Graph Search在这个时候就会弹出G，算法结束，返回$g(G)=6$ ,我们发现这并不是个最优解。
     • 但是使用A* Tree Search的话，仍然会访问G,并返回 $g(G)=5$ ,此时是最优解
     • A Graph Search *只保证完整性，但不保证最优性。

Consistency 和Admissbility

我们知道Admissible可以保证A树搜索方法可以得到最优解。其中心思想就是：启发函数的估计值 $\leq$ *真实的代价

如下图：$h(A) = 4$ ，它是小于等于A到G的真实代价4的。

那么为了保证A Graph Search也可以保证得到最优解，我们提出Consistency。*这是一个比Admissible更加严格的Heuristic。其中心思想是：

$$h(A)-h(C)\leq \text{cost}(A\rightarrow C)$$

用汉语来说，就是估值的边权，需要小于等于真实的变权。我们举个例子：下图中，$h(A)=4,h(C)=1$ , 但是 ， $h(A)-h(C)=3> 1$ 这就不满足 consistency的标准

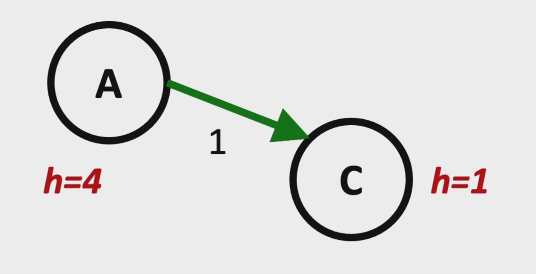
因此，如果要满足一致性，$h(A) $ 至少是小于等于2的。

Consistency 的最优性证明

前提：Consistency

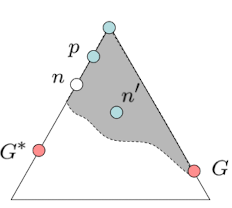
情况如上图，n和n’ 对应的是同一个点的不同路径状态，n比n’更优。

假设：p是n的祖先且p在队列中，n’已经被访问了。在n’被弹出时，p在队列但未弹出。

目标：通过反证法 证明n要先于n’被弹出

1. 因为$f(p) = g(p)+h(p)$, $f(n)=g(n)+h(n)$ $f(n) -f(p) = g(n)-g(p)+h(n)-h(p)$

我们知道，$g(n)-g(p)$ 就是三角形上n点到p点的距离. 另外，由Consistency可知，$h(p)-h(n)\leq Cost(p\rightarrow n)=g(n)-g(p)$ 。

因此$f(n)-f(p)>0$ ,$f(p)<f(n)$ .

于是，由A*算法可知，p会先于n节点展开

1. 又因为n’是次优节点，因此$f(n)<f’(n)$，所以$f(p)<f’(n)$

这种情况有矛盾出现：$f(p)<f’(n)$，说明p应该在n’前被展开。

这与假设里n’先于p被展开相悖，所以假设不成立。

这证明了对于任何一个点，它的最优节点一定是最先被展开的。

A* 算法总结

A-star算法总结

• Tree search
  • 当启发是admissible时，A*保证最优性
  • 当h=0时，A*退化成UCS算法
• Graph search
  • 当启发是consistent时，A*保证最优性
  • 当h=0时，同样A*退化成UCS算法

• Consistency 包含了admissibility

• 从实践经验来说，大多数admissible的估计都可以做到consistency。

Local Search algrithms

在很多优化问题中，我们只要求找到目标状态，对找到目标状态的路径没有要求。比如：八皇后问题，TSP问题。

局部搜索(local search)是解决这类问题的一个方法：从一个初始解出发，搜索当前解的邻域，如果有更优的解则移动至该解并继续搜索，迭代这个过程直到找到局部最优解。

Hill-climbing 爬山算法

代表性算法——爬山算法：

• 找最好的邻居状态节点。如果比当前节点状态要大，就将其设为新的当前节点。

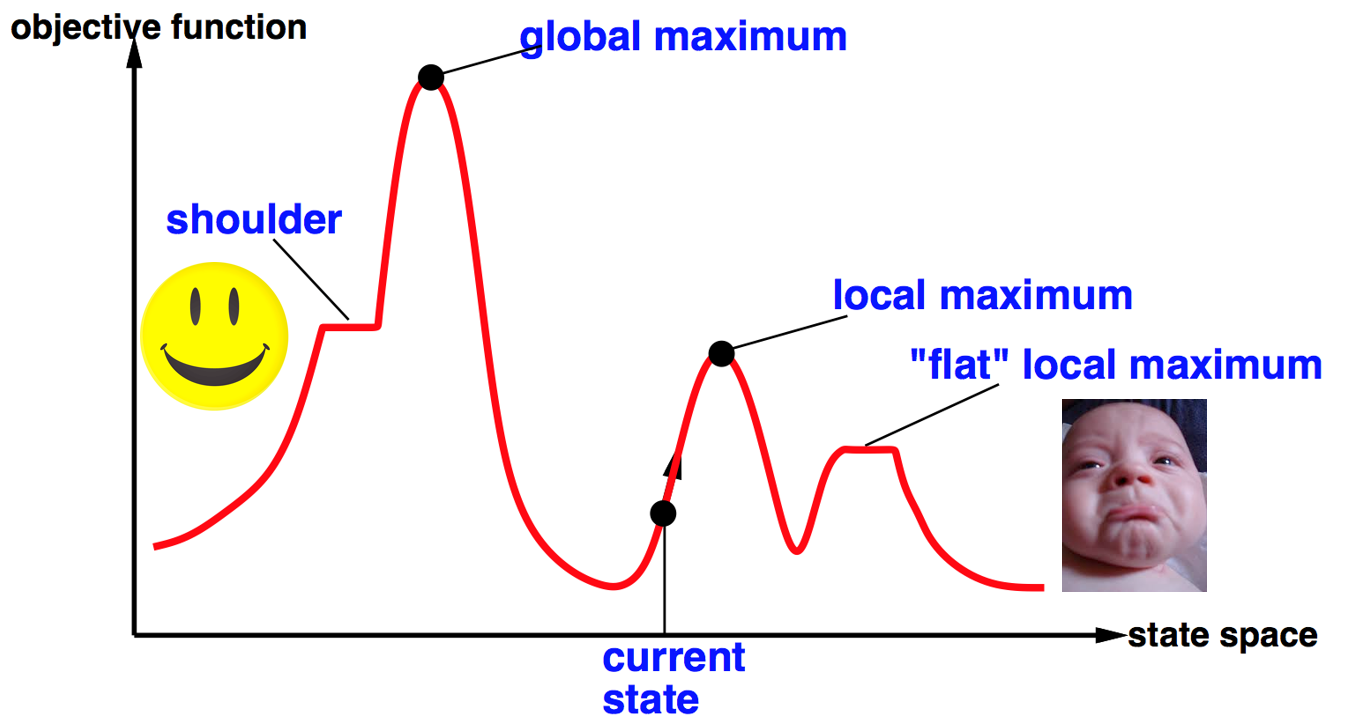
怎么避免陷入局部最优？

• random restarts，多试几种起始点。
• random sideways moves，允许平移。可以逃离shoulder，但是逃离不了local maximum, flat local maximum。
• first choice，不一定要选择最高的邻居节点，而是随便选一个比当前状态高的。

总结：引入随机性

爬山法用于八皇后问题

举例，八皇后问题中如果用“冲突数”评价状态会存在很多shoulder（邻域状态与当前状态冲突数相同）。因此有必要引入sideway move。

Simulated annealing 模拟退火法

模拟退火本身的动机，在于让金属凉下来的方式达到一个low-energy的状态。

基本想法：在一开始的时候允许它往值更低的方向走，一开始温度高允许算法出现错误的移动，希望它能够跳出局部的最优。随着时间的推移，温度下降 ，减少允许它错误移动的机会和次数。

一句话总结，开始允许犯错，目的是为了跳出局部的最优，渐渐地不允许犯错了，希望找到全局的最优。

t指的是温度，按照指数级别的方式降低。按照某一个概率允许向下移动，该概率随t减小概率逐渐降低。

保证最优解，只要温度降低速度“足够慢”（按照指数级别下降exponentially slowly），就可以保证收敛到最佳状态（证明思路是模拟马尔可夫链）。

Local Beam Search集束搜索

对local search算法进行k次拷贝，对当前的k个状态生成状态的所有后继节点进行展开，在其中选择最好的k个后继节点。

与运行k次local search算法的区别在于Beam search每次只选择k个状态进行展开，选择的时候有做过对比，而退火算法是用纯粹random的方式进行选择。

Genetic algorithms 遗传算法

仿照基因进化原理，保留最优状态。

遗传算法实际上是随机束搜索的变形, 通过把两个父状态结合生成后继。

种群：种群中的每个个体都是潜在解 ，可以看成所求问题解的集合。

个体表示： 染色体， 实际就是状态的表示 ，每条染色体也可以看成所求解问题对应的一组解。

适应度函数fitness：表示解的好坏程度 。

选择selection（利用）：根据适应度选取比较好的解优先进行两两繁殖 。

交叉cross-over（利用为主+探索）： 选取一个杂交点， 两边染色体互相交换 。

变异mutation（探索）：每个位置都会小概率发生变异 。

类比成兔子，遗传算法是一群吃了失忆药片随机分布在地球上的某些地方的兔子们。他们不知道自己的使命是什么。但是，如果你过几年就杀死一部分海拔低的兔子，多产的兔子们自己就会找到珠穆朗玛峰。这就是遗传算法。

在连续性的空间做局部搜索算法