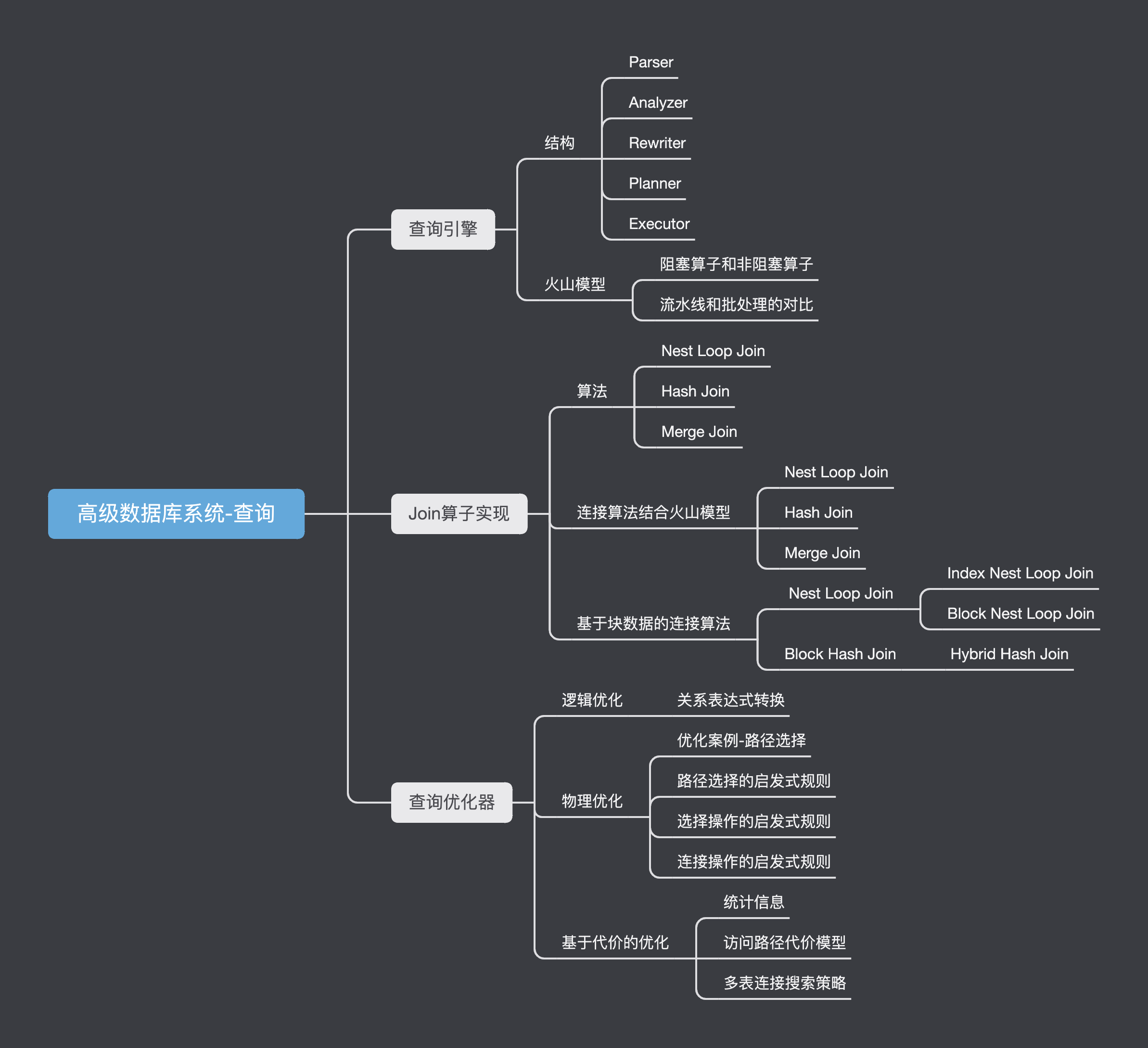
查询
执行引擎
数据库查询可以看做是对数据集合做运算,运算的基本单位是算子。比如投影、扫描、选择、连接、排序等
在关系数据库及其基本实现原理 这篇博客中,我们初步了解了几种算子的功能以及如何实现的。
现在我们来介绍一下在执行查询的流程:
- 首先SQL语言会被解析,并得到好几种不同的查询方案(plan)。 SQL$\rightarrow$ Plans 的过程被称为 Interpretation
- 然后引擎会找出最佳的哪个执行方案。Plans$\rightarrow$ Best Plan 的过程被称为Query Optimization
- 最后引擎会执行这个方案,并返回结果。Best Plans $\rightarrow$ Results 的过程为成为Query Execution
过程如下:
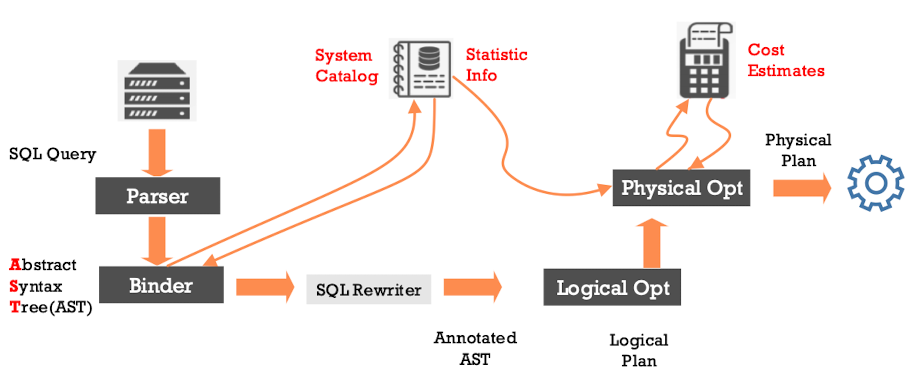
- 从逻辑上讲:
- 查询 $\rightarrow$ 语法树 $\rightarrow$ 逻辑优化$\rightarrow$ 物理优化 $\rightarrow$ 查询执行
- 逻辑优化是关系代数的等价变换
- 物理优化是访问路径的选择,算子执行路径的选择
- 在实现中
- 很可能发生耦合
- 查询 $\rightarrow$ 语法树和数据结构 $\rightarrow$ 逻辑优化/物理优化耦合 $\rightarrow$ 执行
下图是PostgreSQL中查询引擎的组成部分:
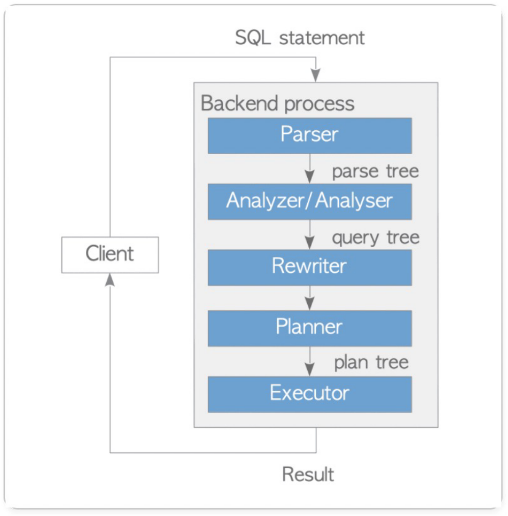
引擎主要可以分为几个组件:
parser
首先是parser,它进行的是编译过程,对SQL进行词法和语法分析
SQL被编译过程中会形成这样一棵 Parse Tree(语法树)
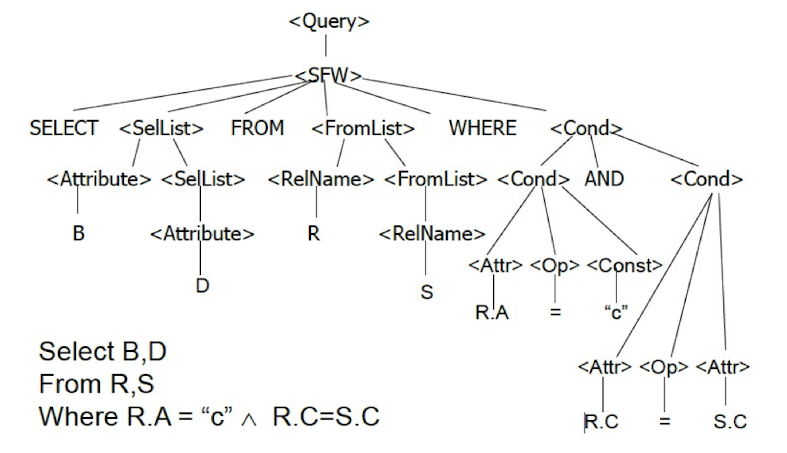
Analyzer
然后,Analyzer会对语法树做语义检查,一共是检查这几个方面:
- 投影列是否存在与对应的关系中
- 属性是否明确?是否有歧义?是否存在?
- 类型检查(int ,double等)
Rewriter
Parse Tree经过 analyzer之后就变成了Query Tree, 在这里面有一个视图表 (蓝色的RTE_VIEW)。Rewriter的作用是展开视图表
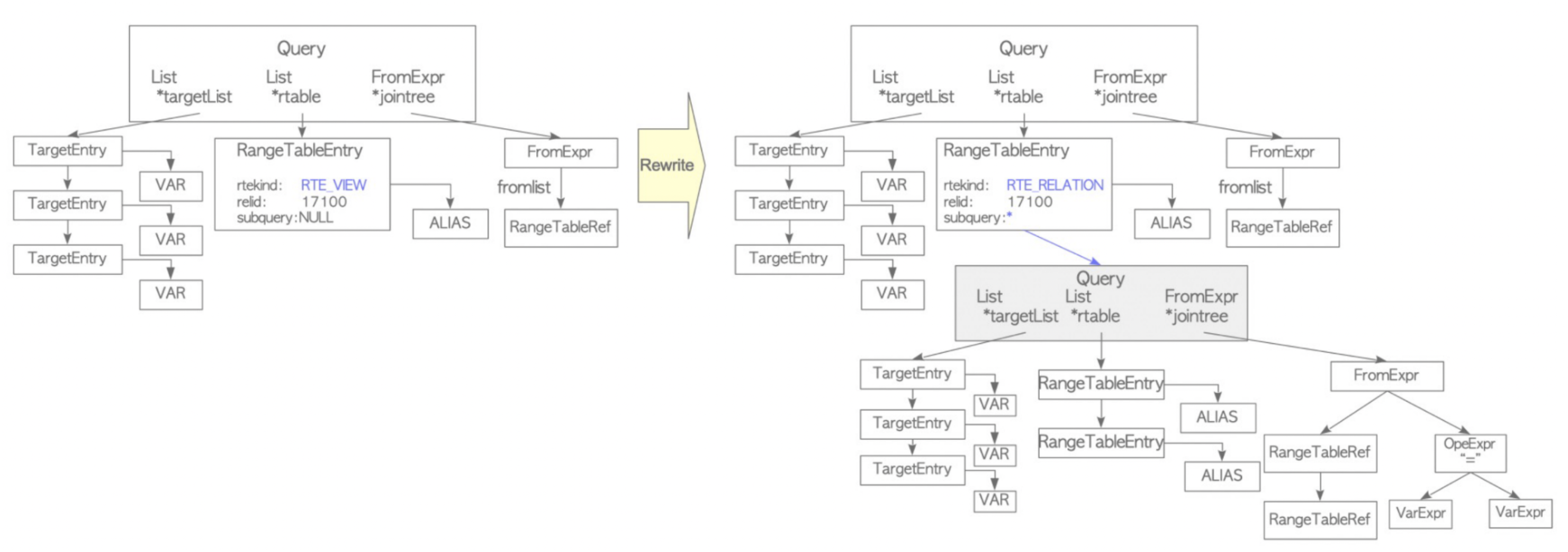
Planner
Planner是对上面的完整的Query Tree进行处理,形成查询计划
1 | SELECT * FROM tb1_a WHERE id < 300 ORDER BY data; |
比如说对上面这句SQL语言,会生成如下一个plan tree
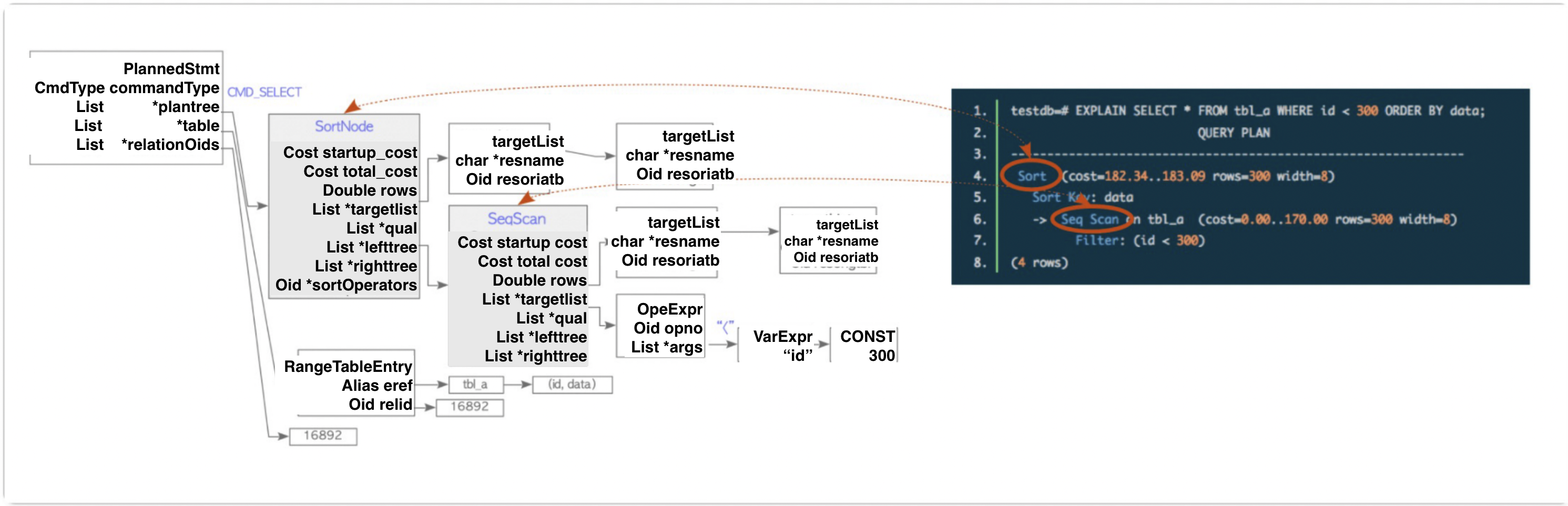
在这个过程之后会进行逻辑优化和物理优化,这部分我们放到最后一节去说。
我们可以使用EXPLAIN功能,输出物理计划:
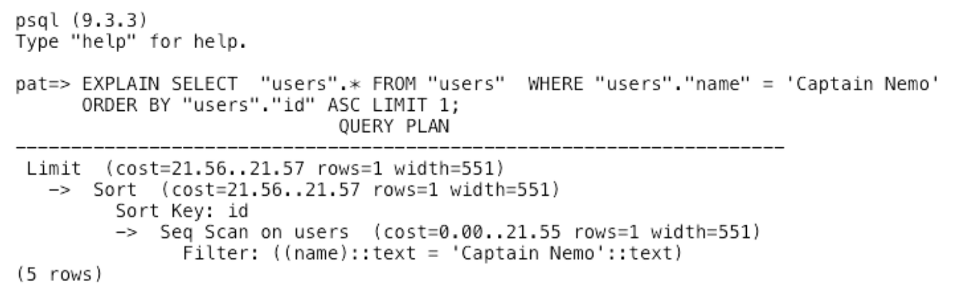
Executor
最后交给执行器去执行,接下来我们就要学习查询执行过程中的火山模型
查询引擎-火山模型
我们从上面看出,物理计划是一颗树形的结构,那么以此提出了火山模型来实现查询引擎的功能。火山模型是一种通用的SQL执行引擎的实现方法,因此很多数据库都会使用。
- 操作流:从树顶依次往孩子节点要数据,直到底层算子提供数据
- 数据流:从叶子依次往上层返回数据
每个数据库操作,都会使用共同的结构:
- Open() : 准备资源,准备获得第一个tuple
- Next(): 一次提供一个数据
- Close(): 释放资源
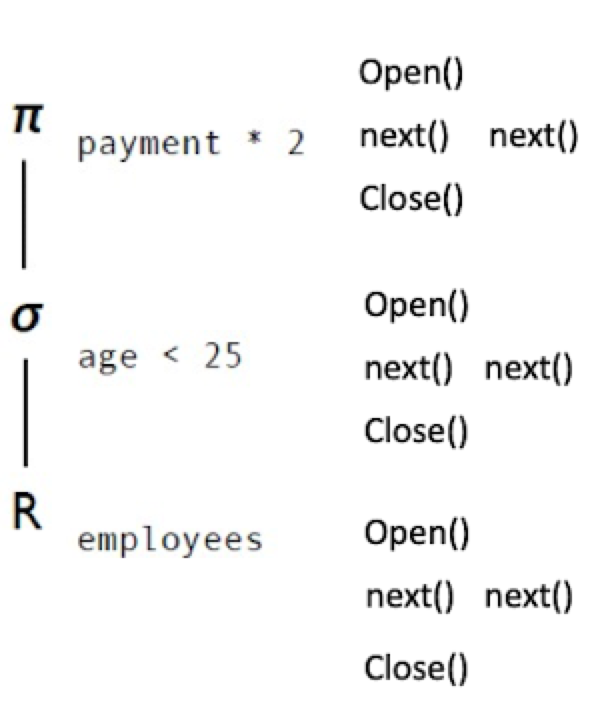
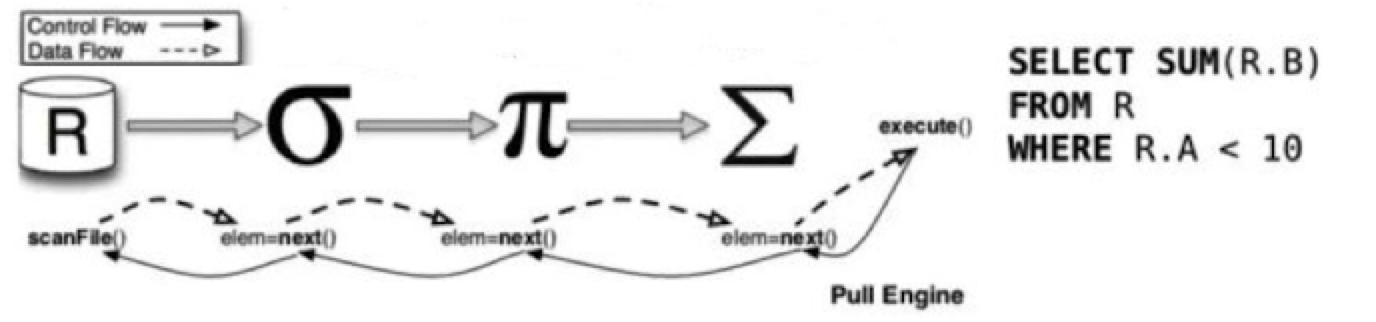
比如说上面这个执行树,投影、选择、扫描算子都有这三个接口。当我的SQL语句想要得到一行结果的时候, 首先会去调用投影的next接口,然后投影的next会去调选择的next接口,而选择的next又会去调扫描的next接口,只有满足了条件的数据才能够向上传递。
总而言之,就是父亲节点去调用孩子节点的next接口,直到获得一条数据为止。比如说第3条数据符合age<25的条件,那么,选择算子会循环调用3次扫描算子的next接口,才会拿到一条符合条件的数据,并向投影算子传递
比如说我们要实现一个排序算子,我们可以这样来实现
1 | sqrt(){ |
阻塞算子
其实,上面的sort就是一种阻塞算子,我们也可以看到sort和扫描是完全两种不同的算子——sort需要拿到所有的数据,而扫描不需要。
因此,我们称 要把数据全部拿到再执行的算子称为阻塞算子
常见的阻塞算子是:构建哈希表(哈希连接)和排序(合并连接)
优缺点
我们可以首先来对比批处理执行和流水线执行
如果是用批处理的话,我们可以写几个for循环,然后几行代码就可以搞定。虽然效率很高,但这样的可扩展性极差。
但是使用流水线来执行的话,虽然效率很低,但是可扩展。
因此我们可以做出预测:
火山模型的优点:
- 实现简单易扩展
- 节省内存资源
缺点:
- 冗余的流控指令
- 效率低:虚函数嵌套,CPU的分支预测不友好
流水线在内存数据库中的优化
这实际上是一个并行的概念,也就是一次next并不是只取一条数据,而是取一批数据:
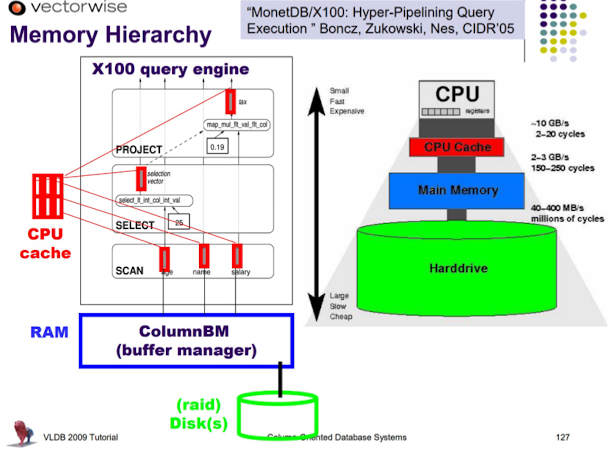
Join 算子实现
这里我们主要学习连接算子join的实现过程。两张表的Join的效果如下
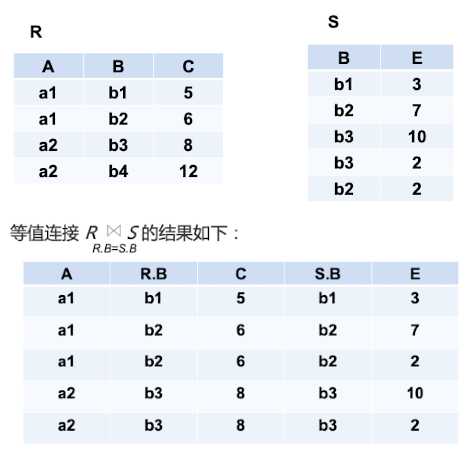
连接算法
连接算法一共有三种:Nest Loop Join、 Hash Join、 Merge Join. 目的就是将相同属性的pair给找出来
Nest Loop Join
Nest Loop Join就是对 R 和 S 进行双循环匹配。如果 $R\bowtie S$ 的话,R为内表,S为外表
1 | Function : nljoin (R,S,p) |
Hash Join
如果采用Hash Join方法,可以对内表(这里是R表)构建哈希表,然后用S表去做哈希探测
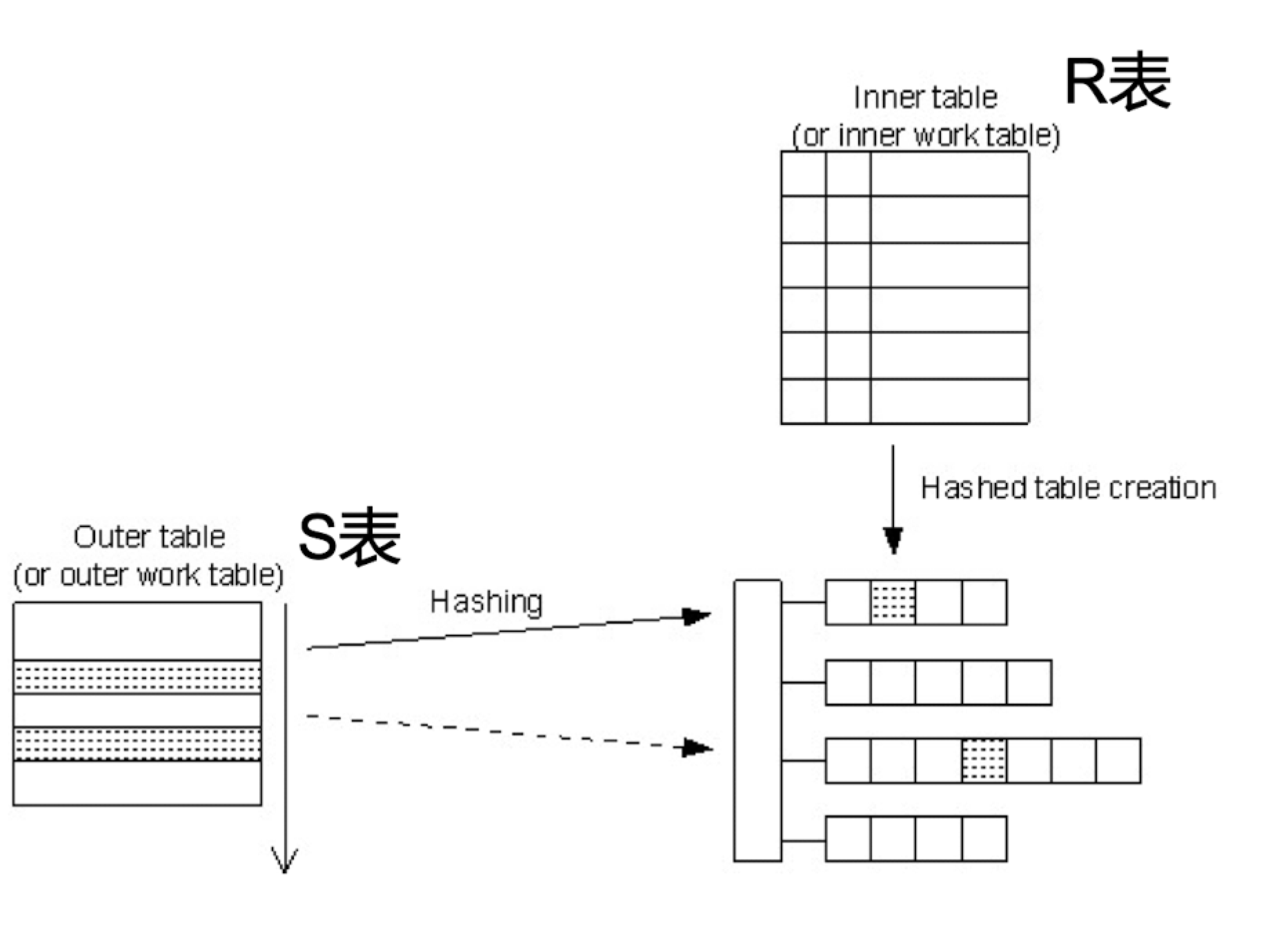
Merge Join
如果采用Merge Join,需要分别对 R 和 S 进行排序,然后用归并算法得到Join结果
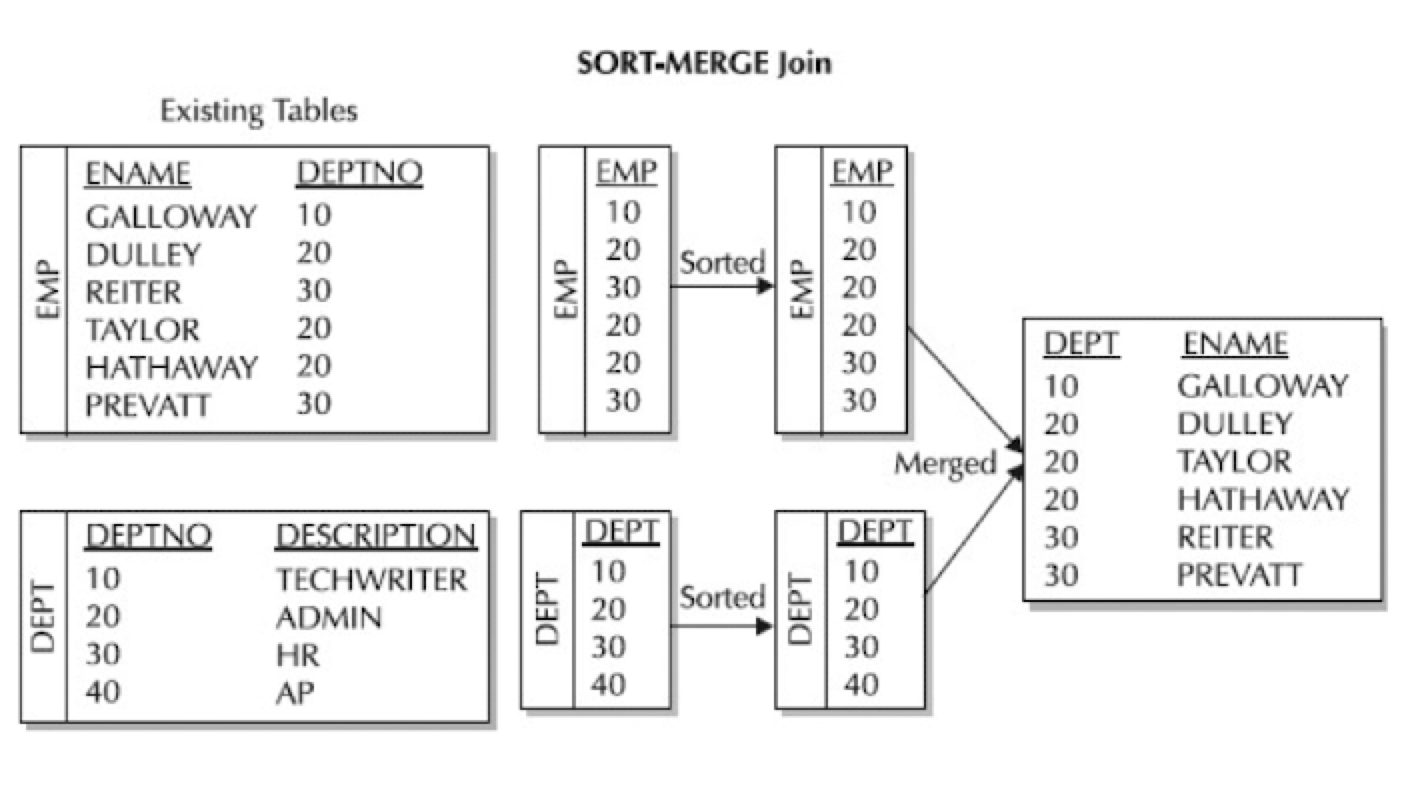
连接算法结合火山模型
现在我们来看三种算法在火山模型下该如何实现。
Nest Loop的火山模型
我们可以简单画出 Nest Loop Join的查询计划表
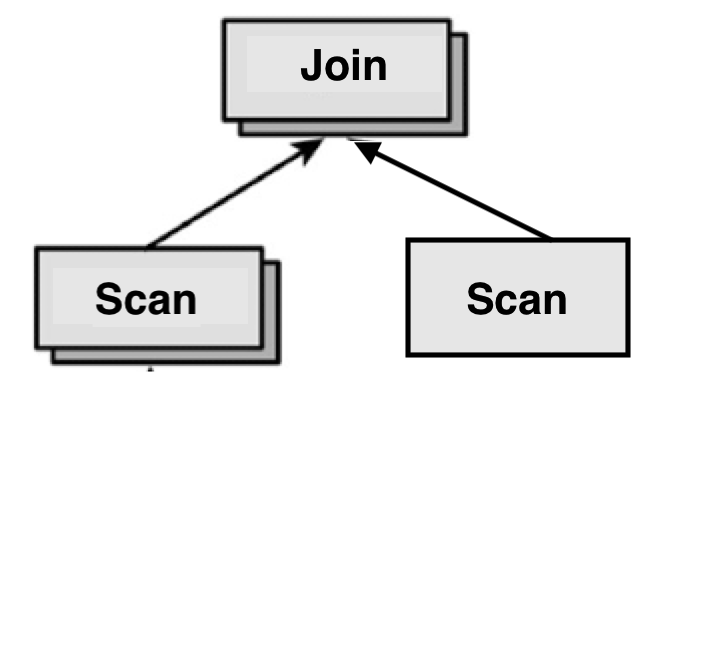
我们看到,由于Join算子需要对两张表进行连接,那么他一定是由两个孩子算子的
事实上,在数据库系统中,有三种不同类型的算子:
- 没孩子的,比如Scan算子
- 单孩子的,比如Sort算子、投影算子
- 双孩子的,比如Join算子
首先我们列出比较简单的open接口和close接口
1 | Function: open() |
1 | Function: close() |
接下来给出next()接口的伪代码,本质上就是两重扫描:伪代码也非常直接
1 | While (r != <EOF> )do |
Hash Join的火山模型
Hash Join 用到了多个算子:Hash算子用来创建哈希表,Hash Join算子用来探索哈希表
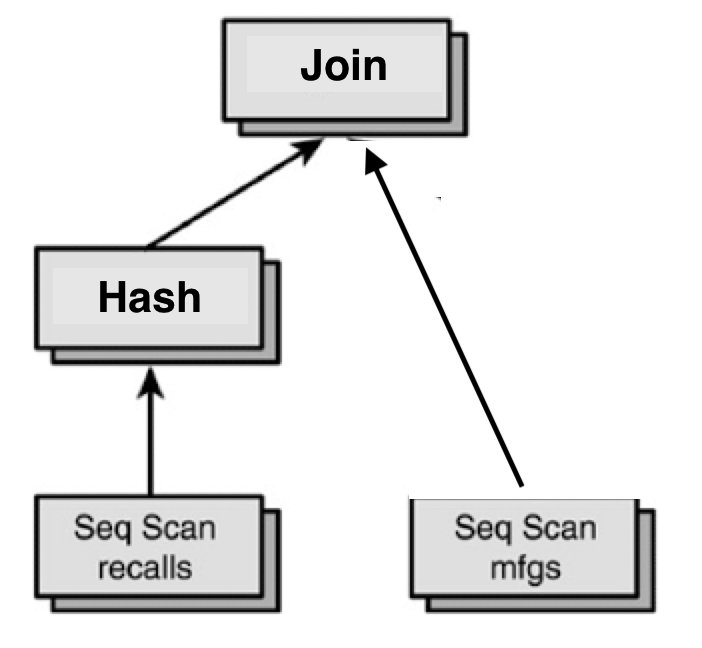
Hash Join的火山模型有两种实现方式:
- 写法1
1 | open(){ |
1 | Next(){ |
在这中写法中,open接口其实是做一个准备工作,也就是将内表打开并将其扫入内存、构建哈希表了。这样在next接口中只需要做扫描即可。实际应用中这种方式更加常见
- 写法2
1 | open(){ |
1 | next(){ |
如果采用这种写法,需要在next的时候多加一层判断,实际上开销是差不多的。
Merge Join的火山模型
Merge Join 用到了多个算子:Sort、Merge Join 等,下面是其查询计划表:
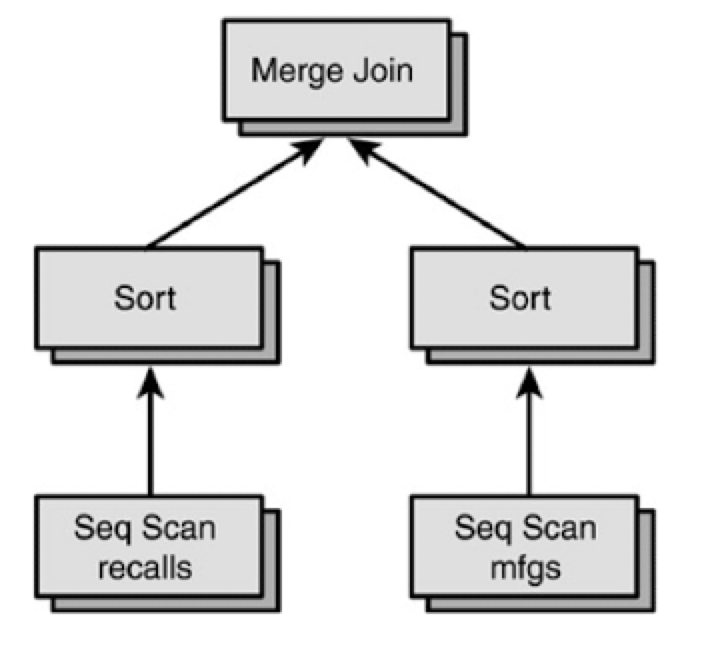
Merge Join 下面有两个Sort算子,负责对两张表的数据进行排序。Sort算子在之前我们说过会维护一个缓冲区,用一个while循环不断地向Scan算子要数据,然后在缓冲区中进行排序。
两个Sort都排序完成后,进行Merge Join算子的操作,也就是会从两个Sort算子各取一条数据,比较它们是否相等,如果相等说明满足条件,return,否则就继续取下面两条数据。
Join算子并不是阻塞算子,Sort算子才是阻塞算子
基于块数据的连接算法
现在很多数据库的底层是LSM Tree,在那种数据库环境下谈基于块数据的算法是没有意义的,这里我们讨论的是传统数据库中的基于块数据的连接方法
由于在传统数据库中,数据库以Block/Page为基本存储单位,因此缓冲区可能会存在内存不足的问题,导致无法将数据全部加载到内存中进行计算。
假设内存有B个Block用于Join,其中一个Block用于缓存Join的结果(在火山模型中并不需要缓存所有结果)。基于上面这种情况,我们再来讨论三种算法的实现
Nest Loop Join
首先我们来回顾一下Nest Loop Join算法:对于 $S\bowtie R$, $S$ 为内表,$R$ 为外表。那么需要做一个双重循环,将$
当块和Next Loop Join结合起来会变成什么样?
我们假定 R 和 S 的blocks数量分别为$N_R$ 和 $N_S$ ,那么对于外表来说,其每一个块都需要放到内存里面一遍,对于内表来说,外表的元素每改变一次,就要将所有的块放入内存中访问一遍,因此总的块访问次数为 $N_R+|R| \cdot N_S$
Index Nest Loop join
实际上我们可以对Nest Loop做一定的优化:改进成了 Indexed Nest Loop Join
对R表的每个数据,直接对S表做Index Scan,以此减少磁盘访问次数和访问数据量。
1 | Function : index_nljoin(R,S,p) |
前提条件是,在S表上的那一列需要对其构建索引。然后,对于R表中的每个元素,对S表做索引的查询,这样复杂度就可以降下来了。对块的访问次数也没有之前多——不用再扫描全表的块$N_s$了
Block Nest Loop Join
我们可以再进行一次优化来减少磁盘的访问次数
假设缓冲区中 $b_r$ 和 $b_s$ 个块用于缓存R和S的数据,$b_r+b_s=B-1$(B为内存可分配的块数量), 剩下1个block是用来存放输出的。
1 | Function: block_nljoin (R, S, p) |
也就是说,一次读入 $b_r,b_s$ 个块读入内存,对其进行比较、连接。
因此,总的磁盘访问次数为: $\lceil N_R/b_r\rceil\cdot\lceil N_S/b_s\rceil $ (默认块是连续的)
访问block数量为: $N_R\cdot N_S$
通常来说,我们会取 $b_r = B-2,b_s = 1$ ,内存中建立哈希表优化匹配 .(如果R表可以一次性全部放进内存,事实上和哈希连接比较相近)
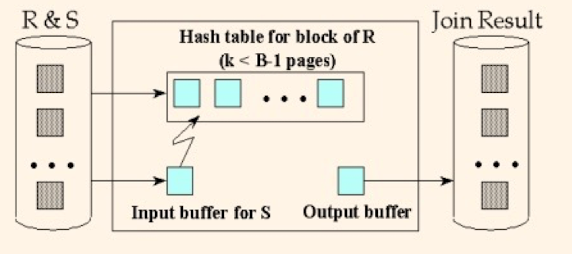
Block Hash Join
如果R表可以完全放入内存,那么R和S只访问一遍,和上面我们说的Nest Loop算法相近
那么如果R表无法完全放入内存的话,就需要对R表进行Block Hash 算法了:
我们可以建 B-1 个桶, 每个桶写满一个Block就刷盘,一个桶可能占多个Block,如下所示:
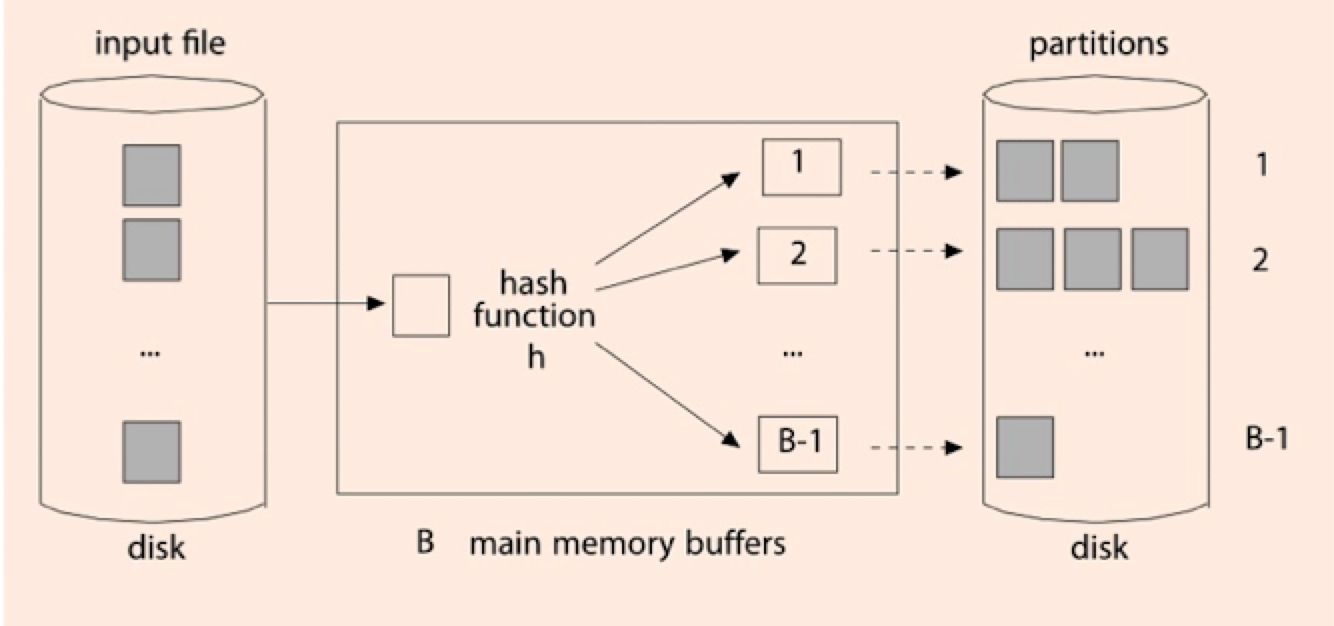
对S表也可以做这样一个Block Hash算法,此时,R表和S表都按照桶分配到磁盘上了。然后,对每个Partition做一趟哈希连接
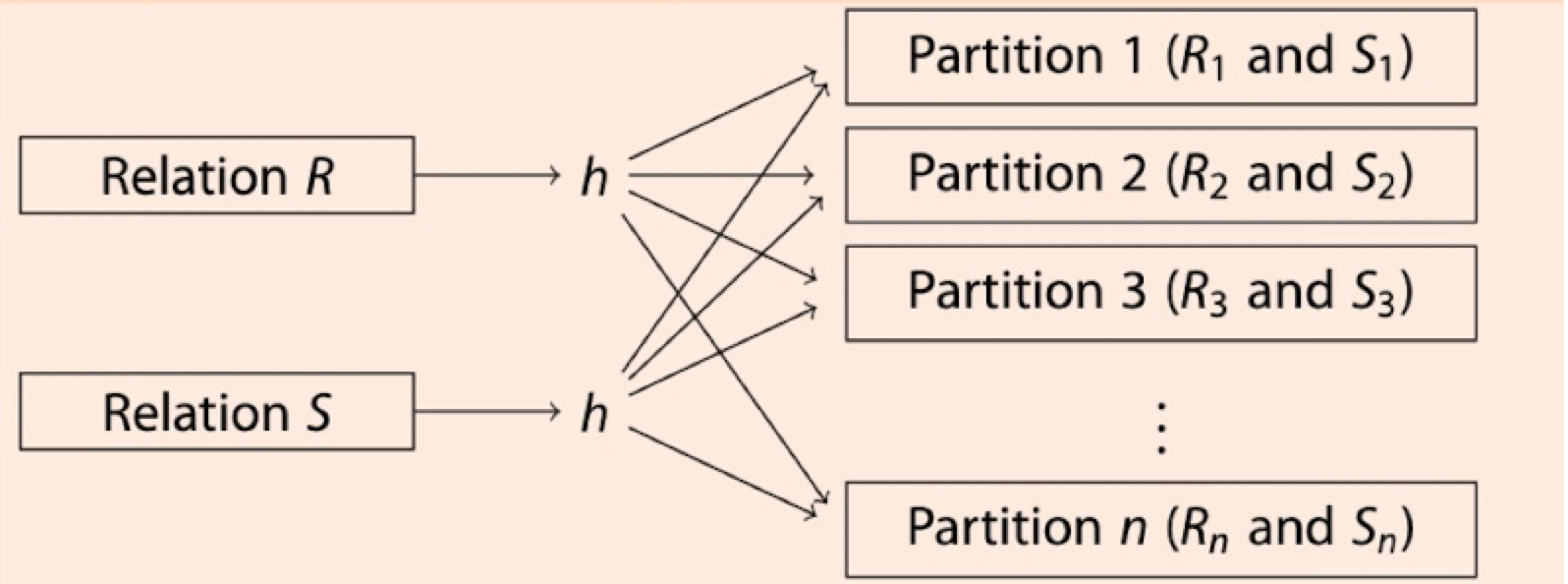
伪代码如下:

当然,这种Block Hash Join算法存在一定的限制
如果每个Partition中R表的Block数量都少于B-1的话,那么算法需要对R、S表进行两趟访问:
- 第一趟将他们读入内存然后进行 Partition, 再将它们刷盘
- 第二趟将每个Partition读入内存,进行Hash Join
但是,如果有Partition中的R表的Block数量大于B-1的话,需要在此基础上继续进行Partition,因此需要多趟算法
如果按照正常的都小于B-1来说,Hash Join访问磁盘Block的次数为:$3N_R+3N_S$ 。 其中,第一趟算法读取和刷盘就包含了$2N_R+2N_S$ ,第二次读取包含了 $N_R+N_S$
Hybrid Hash Join
还可以对Block Hash Join做进一步优化,也就是对部分 Partition 做一趟算法,部分用两趟算法
- 假设构建k个桶,对其中m个桶完全保留在内存中,其他k-m个桶只保留一个block
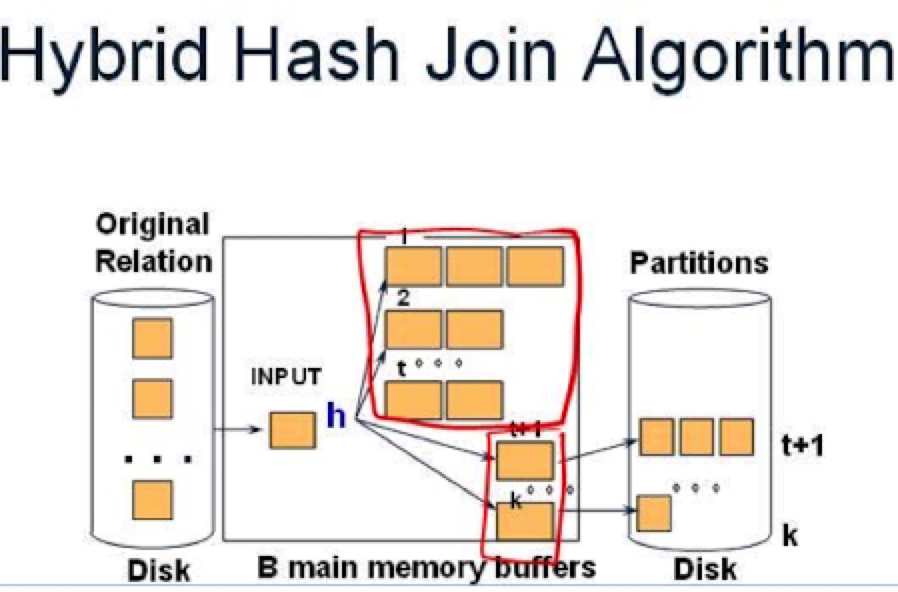
基于块的排序算法
同样的,对于另外一个阻塞算子——排序,如果是基于块的情况下,是怎么样的?
首先,我们有$N_R$ 个块,但内存只有 B-1 个块,$N_R>B-1$ , 此时该如何借助内存进行排序
我们可以从$N_R$ 个块中每次取出 $B-1$ 个块,然后对其进行排序,排序完以后将其刷回磁盘,记为部分1;这样一直记录到部分x。
这样一共会得到 x个排好序的部分,如果$x
因此可能是两趟,也可能是多趟排序
查询优化器
查询优化器的目标是在众多查询计划中选择一个高效的查询执行计划。
- 在集中式数据库中,高效的指标取决于I/O代价、CPU代价和查询的内存开销。
- 在分布式数据库中,评估的总代价=I/O代价+CPU代价+通信代价
之前我们说了有两种优化分类:
- 逻辑优化主要是关系代数表达式的等价变化
- 物理优化更加细致,主要可分三点
- 存取路径:索引、基本表
- 底层操作算子的选择:连接算子的选择、聚合算子选择等
- 多表连接顺序选择(其实也是一种关系代数表达式的变换)
逻辑优化-关系表达式转换
目标:通过对关系代数表达式的等价变换来提高查询效率
如果两个关系代数表达式在每个合法数据库实例上生成相同的元组集,则称这两个关系代数表达式是等价的
逻辑优化案例
下面是一个JOIN带选择的SQL语句
1 | SELECT S.SN |
假定学生-课程数据库中有1000个学生记录,10000个选课记录,其中选修C2课程的选课记录为50个。

这三种方法的评估计划时间的成本差异可能很大,可能是秒级与天级的差异
从代价上看,第三种是最好的,也就是现在SC中做好选择,再去和S表做连接。这比前两种要快很多,几乎可以称为是一条规则了。
常用的等价变换规则
- 连接、笛卡尔积交换律
设E1和E2是关系代数表达式,F 是连接运算的条件,则有
- 连接、笛卡尔积的结合律,设E1,E2,E3是关系代数表达式,F1和F2是连接运算的条件,则有:
当然,这些只是改变表和表之间连接的顺序,可能需要放到物理优化中去,因为在逻辑优化中是看不出来哪个式子代价大的
- 选择与笛卡尔积的交换律, 如果F中涉及的属性都是E1中的属性,则
如果$F=F_1\land F_2$ ,并且 $F_1$ 只涉及 $E_1$ 中的属性,$F_2$ 只涉及$E_2$ 中的属性,则由上面的等价变换规则可推出:
若$F_1$涉及$E_1$ 中的属性,$F_2$ 涉及$E_1$和$E_2$两者的属性,则仍有下式,它使得部分选择在笛卡尔积前先做
实现逻辑优化—基于规则优化
在逻辑优化阶段,我们对查询树依次执行设置的启发式规则,如果满足,则执行规则
– 启发式规则。比如说,选择下推——编码时将选择操作绑定到扫描算子上
– 如何实现?
通常可以调整查询树的数据结构
有些规则需要独特编码方式实现
还有一些比较好用的规则,如下:
把投影运算和其他运算结合
条件化简
利用等式和不等式的性质,可以将WHERE、HAVING和ON条件化简
- 常量传递:使得条件分离后有效实施“条件下推”
Col_1 = Col_2 AND Col_2=3化简为Col_1=3 AND Col2=3
- 消除死码:化简条件,去除不必要的条件
WHERE (0>1 AND s1=5),条件恒假,则不必执行该SQL
- 表达式计算:加快计算效率
WHERE Col_1=1+2变换为WHERE Col_1=3
- 不等式变换:化简条件,去除不必要的条件
a>10 AND b = 6 AND a>2化简为b=6 AND a>10
- 谓词传递闭包:加速计算,有效实施“条件下推”
a>b AND b>2推导出a>b AND b>2 AND a>2
子查询展开
又称子查询上拉,实质是把某些子查询重写为等价的多表连接操作
优势:连接方法和连接顺序选择更加灵活
比如说:
1 | SELECT * FROM t1, |
可以被优化为:
1 | SELECT * FROM |
因为第一种的方法,相当于t2表给限制了一部分,那么在选择的时候就没那么灵活。但是第二种方法就可以在WHERE中更加灵活地组织条件。
外连接消除
- 右表存在非Null条件
SELECT * FROM T1 LEFT JOIN T2 ON T1.c1 = T2.c1 WHERE T2.c2 > 0
注意这里SQL执行顺序是先做JOIN,再做选择。通常使用外连接的话可以降低失误率,但外连接的代价比非外连接要大很多。那么在做查询优化的时候就可以消除外连接,然后把选择可以优化为:
SELECT * FROM T1,T2 WHERE T1.c1 = T2.c1 and R.c2>0
- 满足传递性链式非NULL条件
1 | SELECT * FROM T1 |
可以优化为:
1 | SELECT * FROM T1,T2,T3 |
物理优化
逻辑优化改变查询语句中操作的次序和组合,不涉及底层的存取路径
对于一个查询语句的算子有很多实现方案,它们的执行效率不同
物理优化就是要选择高效合理的操作算子、数据访问路径和查询树结构,求得相对最优的查询计划
基于规则的优化
基于代价的优化
优化案例-路径选择
在查询引擎中,选择操作通常由两种实现方法:
- 简单的全表扫描方法
对查询的基本表顺序扫描,逐一检查每个元组是否满足选择条件,把满足条件的元组作为结果输出。这是和小表操作,但并不适合大表
- 索引(或散列)扫描方法
适合条件中的属性上有索引(B+树索引/哈希索引),通过索引先找到满足条件的元组主码或者元祖指针,再通过元祖指针直接在查询的基本表中找到元组
现在来看最典型的SQL查询: SELECT * FROM student WHERE <条件表达式> ,通常有这几种情况
- C1: 无条件
- C2: Sno=’200215121’
- C3: Sage>20;
- C4: Sdept=’CS’ AND Sage>20
如果以C2为例,Sno上如果有索引,那么就可以使用索引得到Sno为’200215121‘ 元组的指针,通过元组指针在student表中检索到该学生。如果没有索引的话,就需要全表扫描了
以C3为例,Sage>20,并且Stage有B+树索引。那么,使用B+树索引可以找到Sage=20的索引项,以此为入口点在B+树的顺序集得到Sage>20的所有元组指针。通过这些元组指针到student表中检索到所有年龄大于20的学生
那么查询优化器该选择哪种方式呢?全表扫描还是利用索引+回表的方式进行查询
- 如果预先知道结果比较少,就应该使用索引+回表的方式。
- 如果最后的结果很多,甚至整张表都是,那么还是全表扫描比较快。因为找那么多索引再去点查的代价非常高
这两种方法如果选的不好,可能是数十倍的差距,因此,代价评估就非常重要了。
现在来看看更复杂的情况:以C4为例,Sdept=‘CS’ AND Sage>20,如果Sdept和Sage上都有索引:
算法一:分别用上面两种方法分别找到Sdept=‘CS’的一组元组指针和Sage>20的另一组元组指针。求这2组指针的交集,将其放到student表中检索,得到计算机系年龄大于20的学生
算法二:找到Sdept=‘CS’的一组元组指针,那么通过这些元组指针到student表中检索,然后 对得到的元组检查另一些选择条件(如Sage>20)是否满足。最后把满足条件的元组作为结果输出。
在数据库中,第一种方法是不会去实现的,通常只会挑选一个属性去做索引查询。因此,问题被简化为三种情况:选择Sdept做索引查询、选择Sage做索引查询、全表扫描。最终选择那一种方法还是要看选择率的高低
- 如果表中只有一个通选学了CS,那么就应该选择Sdept作为索引
- 如果表中Sage>20的同学只有一两个,那么就需要选Sage做索引查询
- 如果选择率都不是很低,那么应该做全表扫描
路径选择操作的启发式规则
对于小关系(<1000行):
- 使用全表顺序扫描,即使选择列上有索引
对于大关系( 对于选择条件是主码=值的查询):
- 查询结果最多是一个元组,可以选择主码索引
对于选择条件是非主属性=值的查询,并且选择列上有索引
- 估算查询结果的元组数目:比例较小(<10%)可以使用索引扫描方法, 否则全表顺序扫描
对于选择条件是属性上的非等值查询或者范围查询,并且选择列上有索引
- 估算查询结果的元组数目:比例较小(<10%)可以使用索引扫描方法, 否则全表顺序扫描
选择操作的启发式规则
对于用AND连接的多路选择条件
如果有涉及这些属性的组合索引, 优先采用组合索引扫描方法
如果某些属性上有一般的索引, 选择选择率最低的一个索引
对于用OR连接的析取选择条件,一般使用全表顺序扫描
连接操作的启发式规则
如果2个表都已经按照连接属性排序
- 选用排序-合并方法
如果前表较小,后表在连接属性上有索引
- 选用Nest Loop索引连接方法
如果上面2个规则都不适用,其中一个表较小
- 选用Hash join方法或内存Nest Loop Join
否则采用Block Nest Loop Join或Grace Hash Join
基于代价的优化
必要条件
- 实现数据统计信息,用于帮助计算代价
核心代价模型
访问路径
多表连接顺序
执行算子(很多情况下使用规则代替)
- 连接、聚集
那么统计信息哪里来?我们可以列出如下几种
统计信息
对每个基本表
- 该表的元组总数(N)
- 元组长度(l)
- 占用的块数(B)
- 占用的溢出块数(BO)
对基表的每个列
- 该列不同值的个数(m)(用于估算Join结果)
选择率(f)
- 如果不同值的分布是均匀的,f=1/m
- 如果不同值的分布不均匀,则每个值的选择率=具有该值的元组数/N
该列最大值/最小值
该列上是否已经建立了索引
索引类型(B+树索引、Hash索引)
对索引(如B+树索引)
索引的层数(L)
不同索引值的个数
索引的选择基数S(有S个元组具有某个索引值)
索引的叶结点数(Y)
访问路径代价模型
全表扫描算法的代价估算公式
如果基本表大小为B块,全表扫描算法的代价cost=B
如果选择条件是码=值,那么平均搜索代价cost=B/2
索引扫描算法的代价估算公式
如果选择条件是码=值
- 如[例-C2],则采用该表的主索引
- 若为B+树,层数为L,需要存取B+树中从根结点到叶结点L块,再加上基本表中该元组所在的那一块,所以
cost=L+1
- 若为B+树,层数为L,需要存取B+树中从根结点到叶结点L块,再加上基本表中该元组所在的那一块,所以
- 如[例-C2],则采用该表的主索引
如果选择条件涉及非码属性
- 如[例-C3],若为B+树索引,选择条件是相等比较,S是索引的选择基数(有S个元组满足条件,选择率)
- 最坏的情况下,满足条件的元组可能会保存在不同的块上,此时,cost=L+S
如果比较条件是>,>=,<,<=操作
- 假设有一半的元组满足条件就要存取一半的叶结点
- 通过索引访问一半的表存储块cost=L+B/2
- 如果可以获得更准确的选择基数,可以进一步修正B/2
多表连接顺序搜索策略
常常使用启发式+基于代价的搜索,比如说枚举、DP算法等,也可以用随机算法
连接顺序常常是树形结构(使用左深树),它有几个好处
- 每个连接算子的右侧输入是一个关系(基本表),而不是连接后的中间结果
- 基于成本的优化是昂贵的,但对于大型数据集的查询是有价值的(典型的查询具有较小的n,通常小于10)
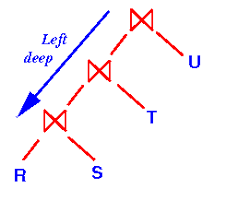
左深树如上图所示,R和S做Join,然后其结果和T做Join,其结果在和U做Join
但是在一些比较新的数据仓库中,会让B和C分别建一个哈希表,然后用A去探索这两个哈希表,实际上用的是右深树
几个难题
为什么查询优化器对代价的估计可能估不准?查询优化器非常难设计。其实都集中在统计信息上。
- 统计信息的选择自动收集与更新非常难,因为数据库在不断运行,数据在不断更新
选择条件下数据的条件分布,(满足A的条件下去选择 B),这样导致原先统计数据在这种情况下是没什么用的。而我们又无法为所有的分布创建一个直方图,因此通常导致估算不准确。
计划不准导致的查询超时无法从理论上避免
总结
逻辑优化
- 定义一些启发式规则
物理优化
先决定访问路径
启发式规则决定连接顺序与连接方式