AI-Adversarial

搜索树1: 博弈

博弈的类型和区分axes

• Deterministic or stochastic? 象棋是确定性的、足球是不确定的
• One, two, or more players? 玩家数量
• Zero sum? 零和、协同合作（例如王者荣耀的队友）
• Perfect information (can you see the state)? 完整的信息（例如整个状态和棋子分布）是否都能完全观察到

Deterministic Games 确定性的博弈

• 状态 States: $S$ (start at $s_0$)

  例如下象棋中棋子的分布

• 玩家 Players: $P={1…N}$ (usually take turns)

  代表玩家的个数

• 行为 Actions: $A$ (may depend on player / state)

• 转移函数 Transition Function: $S\times A \rightarrow S$

  从状态出发经过相应的行为可以到达的一个新的状态

• 是否到达最终状态 Terminal Test: $S\rightarrow {\text{true},\text{false}}$

  一个终止状态的节点，未必最优。

• 最终效用值 Terminal Utilities: $S\times P \rightarrow R$

  得分或者奖励值

• 策略policy: 智能体处于某种状态时该发出的行为，从状态映射到行为 $S\rightarrow A$

Zero-Sum Games 零和游戏

• Zero-Sum Games：

  Agents have opposite utilities (values on outcomes)

  多个 agents 拥有恰巧相反的目标，例如两个agent的分别希望最大化/最小化同一个值并不完全是两方的期望的加和是0

• General Games:

  Agents have independent utilities (values on outcomes)

  协同合作等

Adversarial Search 对抗搜索、博弈搜索

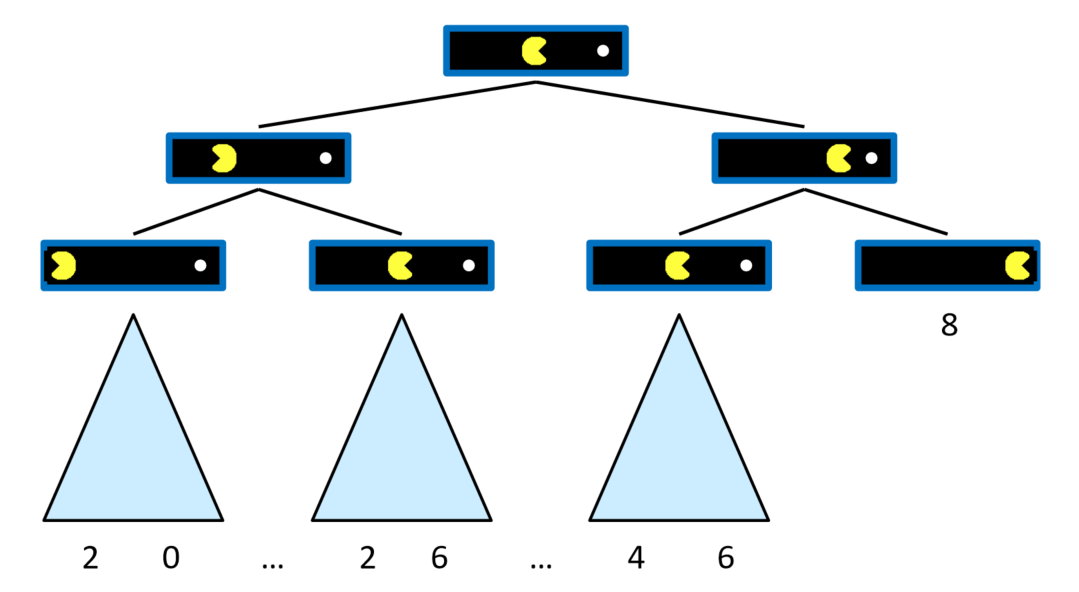
上图是 Single-Agent Trees 一个智能体对应的搜索树。左边的状态表示往左移一步，右边的状态表示往右移

Value of a State 状态的价值：从当前状态出发能够获得的最好效用值 The best achievable outcome (utility) from that state

Non-Terminal States 的状态的价值也是孩子节点状态中最好的value值

$$V(s) = \max_{s'\in\text{ children(s)}} V(s')$$

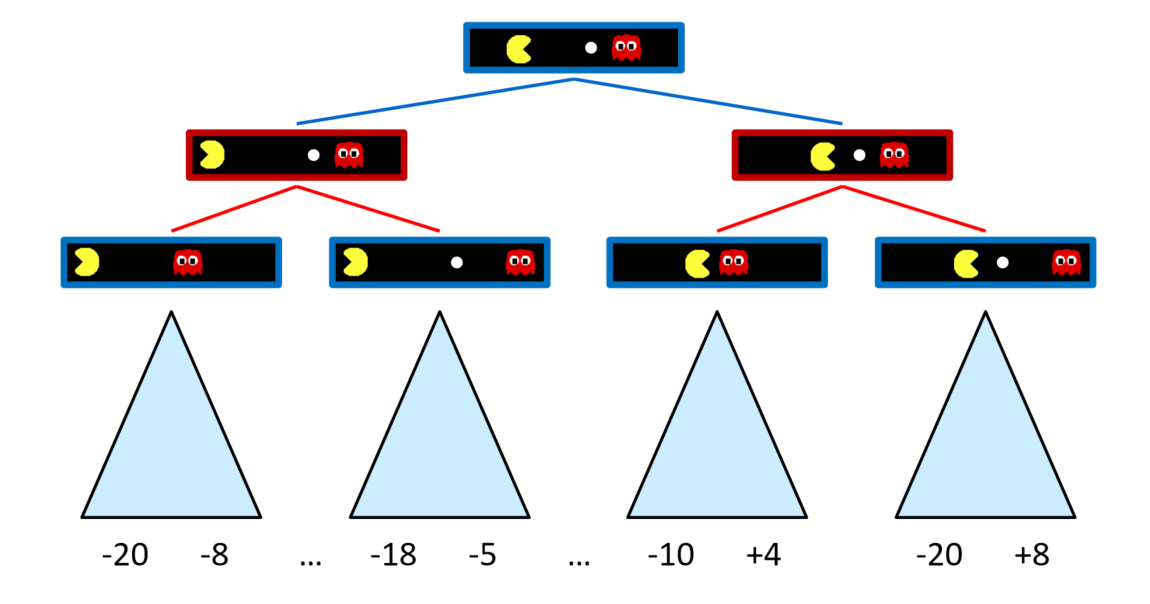
Adversarial Game Trees。存在对抗，一方走完另一方走。鬼希望吃掉Pacman， Pacman希望吃掉豆子。不同层的目标不一样，轮流希望最大化各自的效用值。通过交替的方式对状态展开。

Minimax Values：轮流进行min和max的操作

• 对Pacman来说 States Under Agent’s Control：希望最大化 Pacman 的收益 ，最大化后继节点的状态价值

$$V(s) = \max_{s'\in\text{successors(s)}}V(s')$$

• 对鬼来说States Under Opponent’s Control：希望最小化 Pacman 的收益，最小化后继节点的状态价值

$$V(s) = \min_{s'\in\text{successors(s)}}V(s')$$

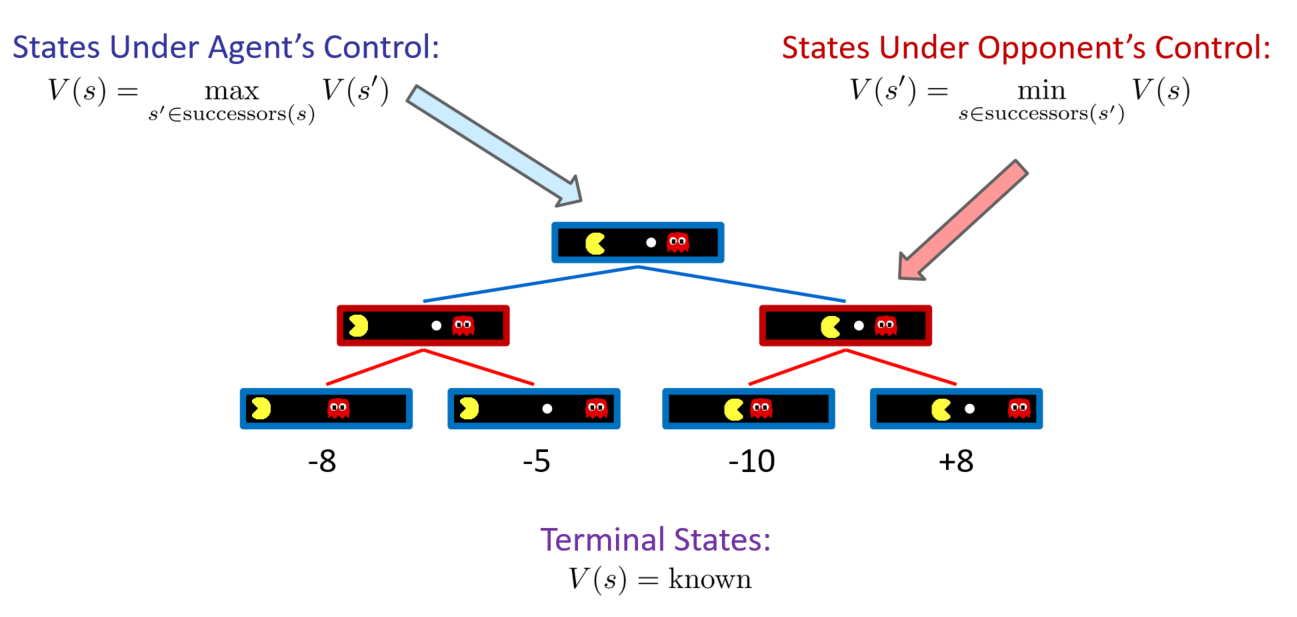
Adversarial Search (Minimax) 对抗搜索

是在树上的搜索。计算非terminal的每一个节点对应的Minimax值，蓝色上三角表示希望最大化效用值，红色的下三角表示希望最小化效用值。由孩子节点的效用值得到。

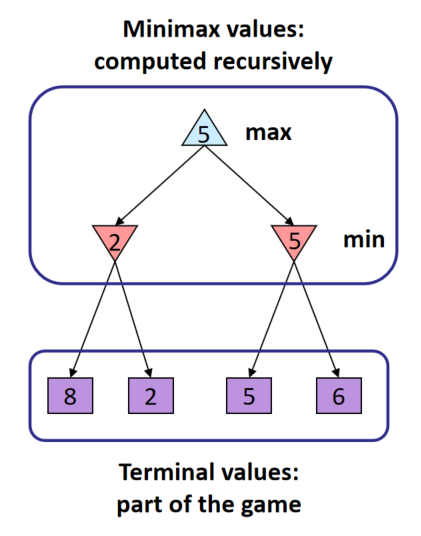
对每一个给定的状态，希望求它的所有后继的最大/最小值。由于是Minimax问题，对每个希望求最大/最小值的节点来说，它的后继相应的希望求最小/最大值。

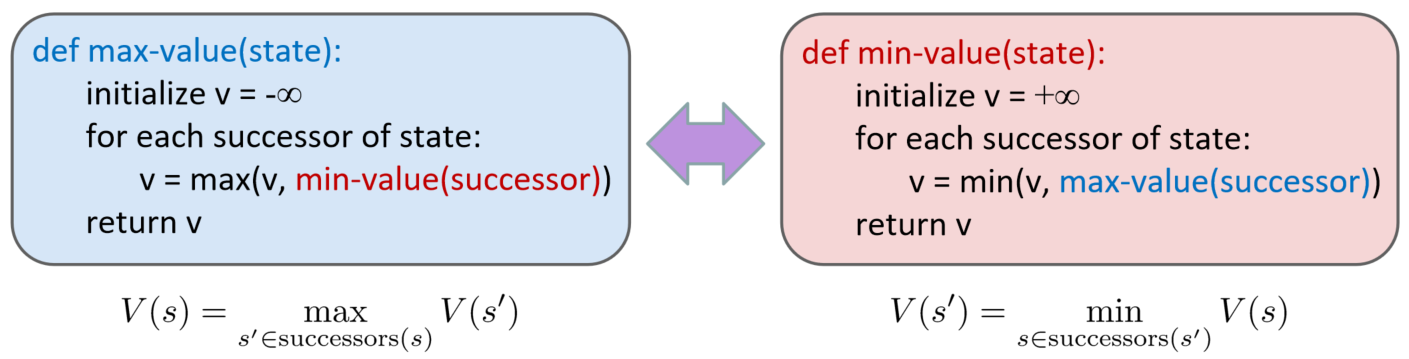
对terminal状态来说，直接返回最终的值。否则分别调用max-value或者min-value函数。

搜索树的提速方式

我们首先来看看没有剪枝的情况下搜索树得到的结果：

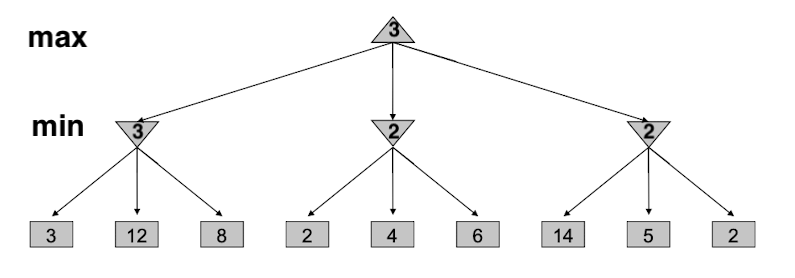
但是，我们如何减少搜索的次数呢？答：进行剪枝

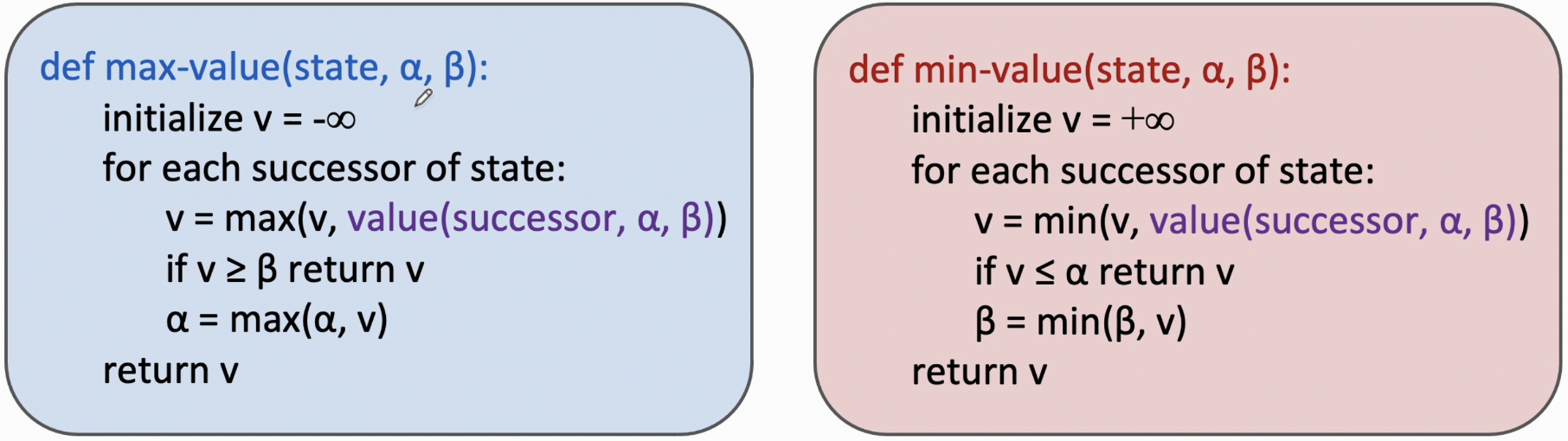
为了提升搜索树的搜索速度，我们可以对其进行 $\alpha-\beta$ 剪枝，其中：

• $\alpha:$ Max’s best option on path to root , 即 $\alpha$ 是上限
• $\beta:$ Min’s best option on path to root，即$\beta$ 是下限

和普通搜索树算法的区别就在于引入了$\alpha,\beta$ 两个值

我们结合具体的例子来看：

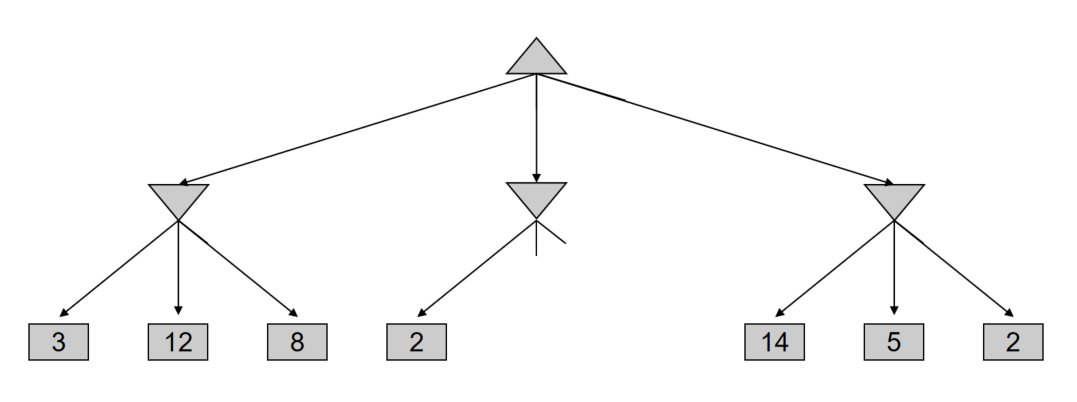
首先，我们还是将最左边的节点的最小值3计算出来，此时根节点的值暂且为3，即$\alpha=3$；然后，我们需要计算中间节点的值, 为此我们需要遍历其子节点，当我们读取到第一个子节点为2的时候，那么不管后面的孩子节点的值是大于2还是小于2，中间这个节点的值一定是小于等于2的。而且2已经比根节点3小了，由于根节点求的是max操作，因此当我们读取到2的时候，其实已经不需要再去读取后面的孩子节点了，这棵子树相当于被废弃了。

也就是说，在这一层因为求得是 min值，使用的是min-value函数， 因此当看到$ 2=v<\alpha=3$ 的时候，就可以直接范围 $v$ 了，完成剪枝

对于最右边这颗子树，首先读取到的是14，14是大于根节点3的，但我们并没法判断后面是否有比3小的数，因此我们无法进行剪枝，仍然需要读取。

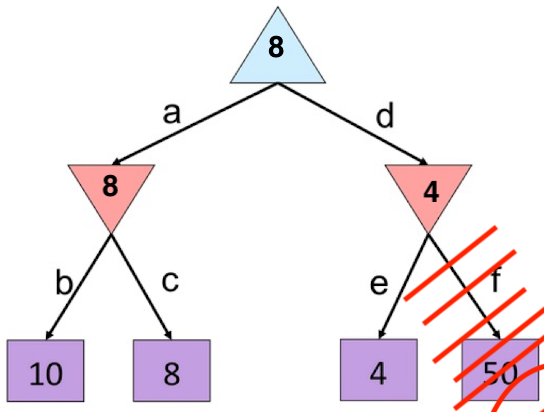
剪枝后的搜索树如下图所示：

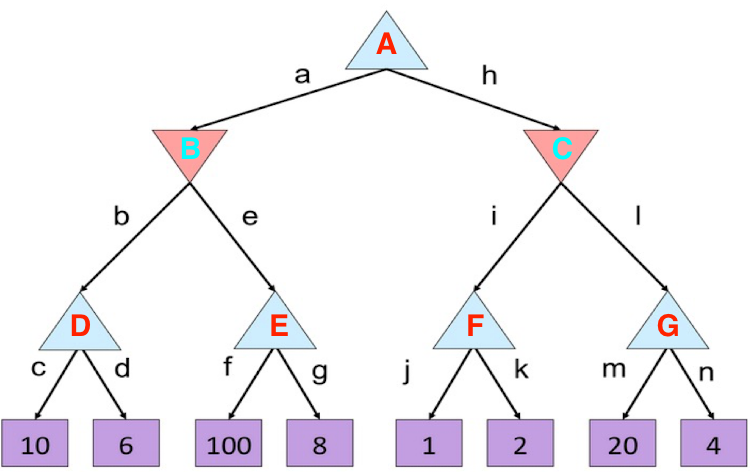
Quiz

1. 

最左边的孩子都需要遍历的，得到$\alpha=8$ ，右孩子的第一个数值是$4<\alpha$ ，因此可以进行剪枝，直接返回4

1. 

结果：

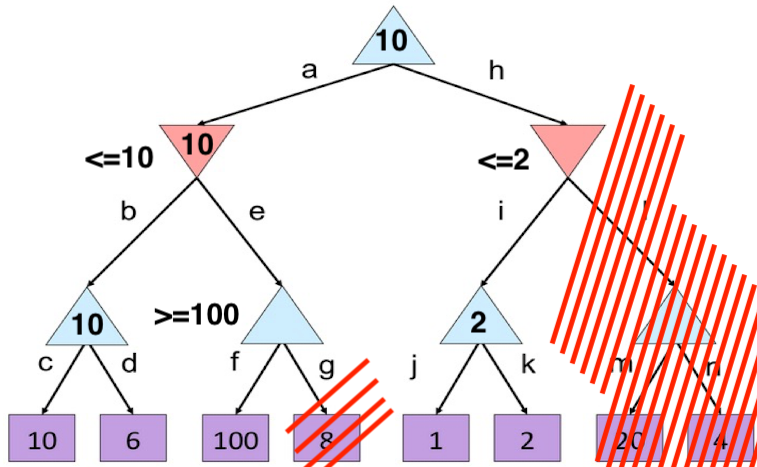
1. 首先，遍历最左的这颗子树，得到10和6的最大值为10，因此设定了$\beta = 10$ ，
2. 读取f节点之后，发现等于100，是大于$\beta=10$的，因此，可以直接剪枝
3. 因此得到了节点B=10，同时可以得到 $\alpha = 10$
4. 读取右边的子树，发现F节点的值是2，而$2\leq \alpha=10$ ，因此直接可以剪枝，G节点可以不去探索了

性质

$\alpha-\beta$ 剪枝的性质：

1. 中间节点的值可能是错误的。

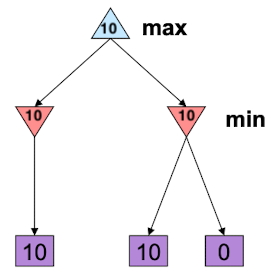
比如说下图，通过左子树，得到$\alpha=10$ , 然后扫描右边的子树，发现左孩子满足 $10\leq \alpha$ ，因此直接返回。但是，事实上左子树的根的真实值应该等于0，这里还没有读取到0就被剪枝了，因此可能是错误的

1. 合适的叶子结点的顺序可以提升搜索树的速度。因为如果是按从小到大的顺序排列的话，可能读取一个叶子就可以完成剪枝操作；但是如果按照从大到小的顺序来排列，可能就需要读完所有叶子结点。
   • 这样可以降低一点时间复杂度，但是对于象棋这种搜索空间特别大的情况，使用$\alpha-\beta$剪枝还是不够的

Resource Limits

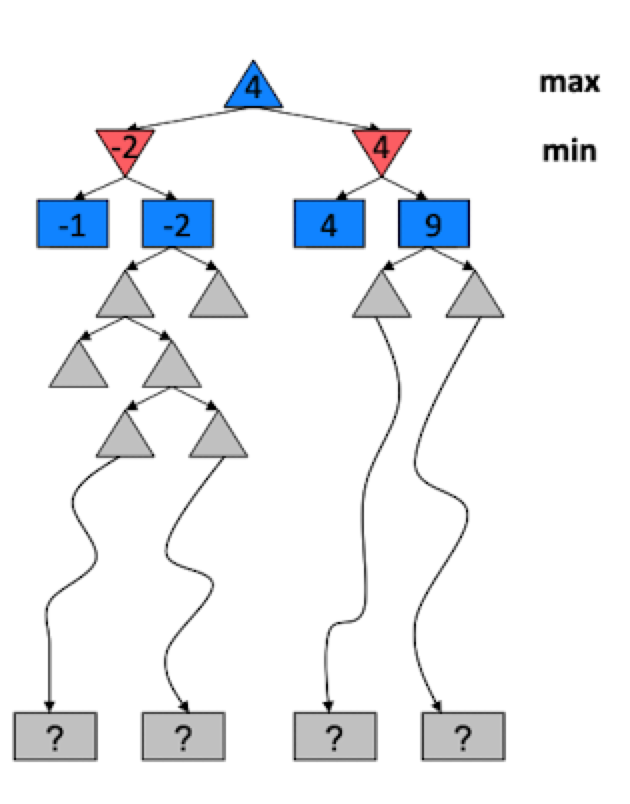
问题： 在现实情况中，很难沿着这棵树去搜索叶子结点

解决办法：除了$\alpha-\beta$ 剪枝之外，还可以限制搜索的深度。比如上面这颗树，我们可以只搜索到第二层后就停止。这时候就没有中间节点的效用值了。那么怎么得到第二层的值?

我们可以引入一个 Evaluation Function，他可以估计中间节点的效用值，如上图所示。

因此，我们引入的Evaluation Function的估计精度就非常重要了，如果估计完全准确，那么就不需要再增加接下来几层节点的访问开销了。

例子：在象棋比赛中，假设我们有100秒，每秒可以探索1万个节点。因此，每回合我们可以探索 1 million 的节点。借此我们大致可以再搜索树里面探索8层，这已经可以得到很好的结果了。

同时我们要知道，限制层数的搜索方式，和层数的多少有着密切关系。搜索的层数越深，那么非叶子结点的估计也就会越准确，越有可能返回真实的结果。

Evaluation Functions

理想的Evaluation Function可以返回完全正确的估计

比如说，我们可以采用线性加和的方式对当前状态的效应值进行估计

$$Eval(s) = w_1f_1(s) + w_2f_2(s)+\cdots+w_nf_n(s)$$

举个例子，我们以象棋为例，我们可以把$f_1(s)$ 设置为 白色queen的数量减去黑色queen的数量，把$f_2(s)$ 设置为白色马的数量减去黑色马的数量，以此类推

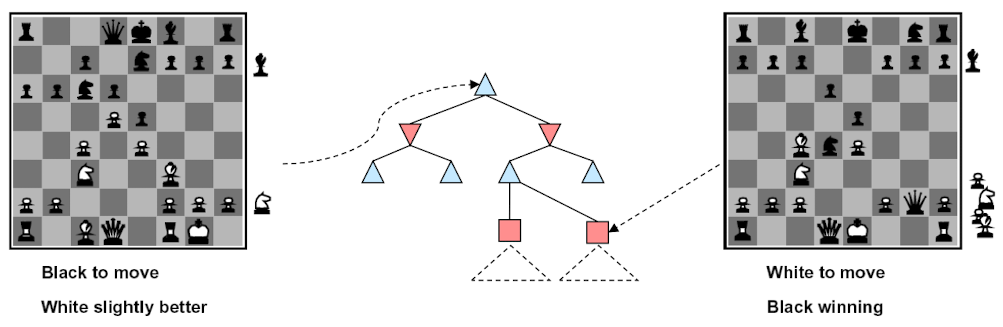
当然，也可以用神经网络来作为Evaluation Function

Depth Matters

首先我们要明白，Evaluation并不是一直准确的。但是随着Evaluation所在的层数的加深，其估计的质量也就会越高。最后，Evaluation可以对特征复杂度和计算复杂度做一个推导，因为如果Evaluation很准，那么就可以剩下很多计算，但是如何构建准确的Evaluation的工作量就要上升了

例1

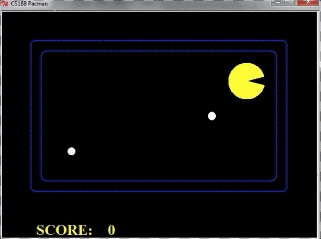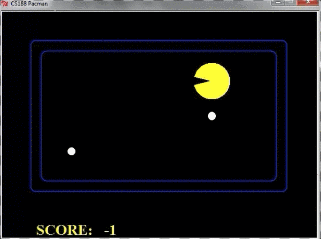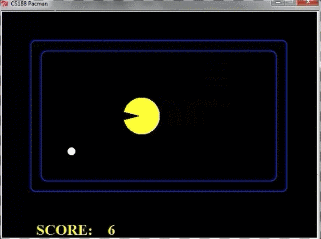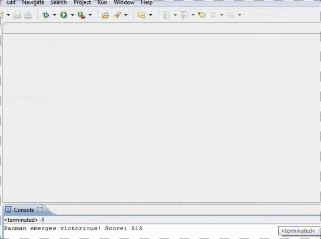
我们看到如果只探索两层的话，pacman的动作如下所示：

我们看到，由于pacman并不知道之后几步的行踪，因此被鬼给吃了

但是如果把探索层数扩大到10层，那么pacman的行动如下所示：

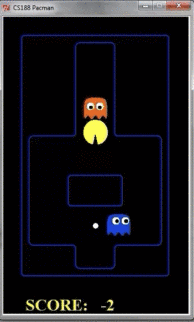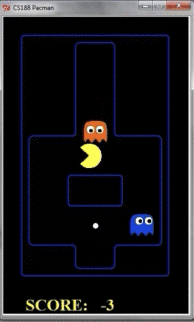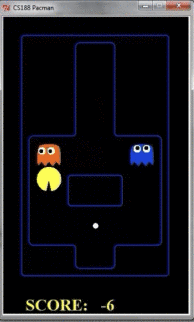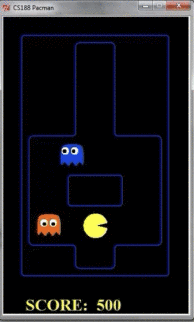
由于Pacman掌握了更多信息，因此鬼捉不到pacman，但pacman可以吃到果子。

例2

我们再来看一个例子，下面这个pacman一直在踱步，但是始终没有下去吃果子，这是为什么呢？这和我们设计的Evaluation有关

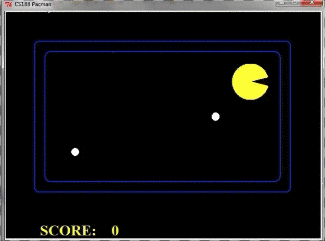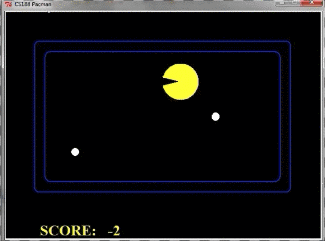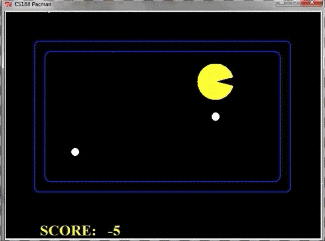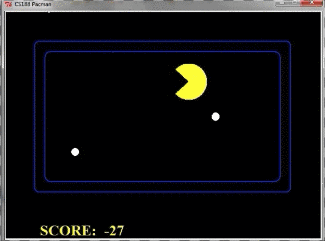
由于我们只考虑了两层，我们将搜索树全部画出来看看：

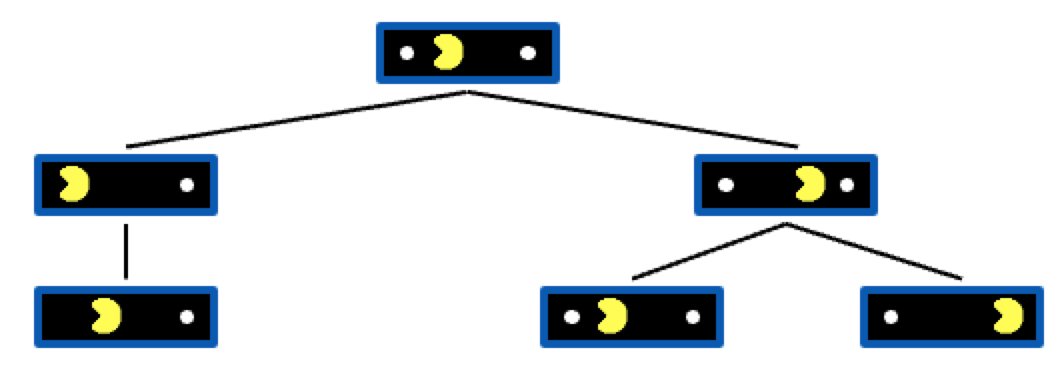
假设吃到果子后可以加上10分那么上面搜索树的值为：

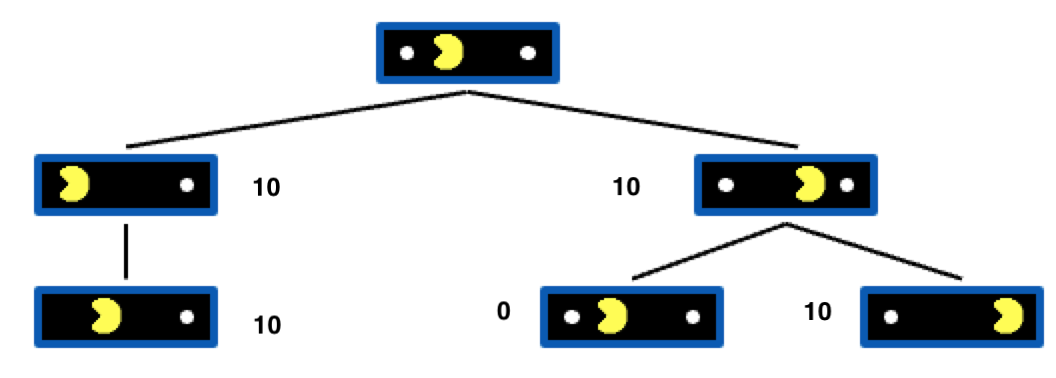
那么对于根节点来说，往左走和往右走的Evaluation是一样的，往左往右都可以，所以一直在左右徘徊。

因此我们需要更准确的Evaluation，我们看到叶子结点中，最左边的情况实际上比最右边的情况更加接近果子，因此我们不妨将这个状态设置为11，那么pacman的行动轨迹就会变成先往左走吃掉果子，再往右走吃掉右边的果子，如下所示：

搜索树 Part2: Uncertainty and Utilities

我们要让自己赢一个游戏的话，肯定需要让自己的利益最大化，由于游戏是存在不确定性的，因此我们需要计算整个游戏的期望。

Expectimax Search

引入

如下图两个游戏，对于画圈画叉来说，游戏下一步的状态是确定的，因此可以用 MinMax Tree来做搜索，但是对于掷骰子，下一步是什么状态是不确定的。

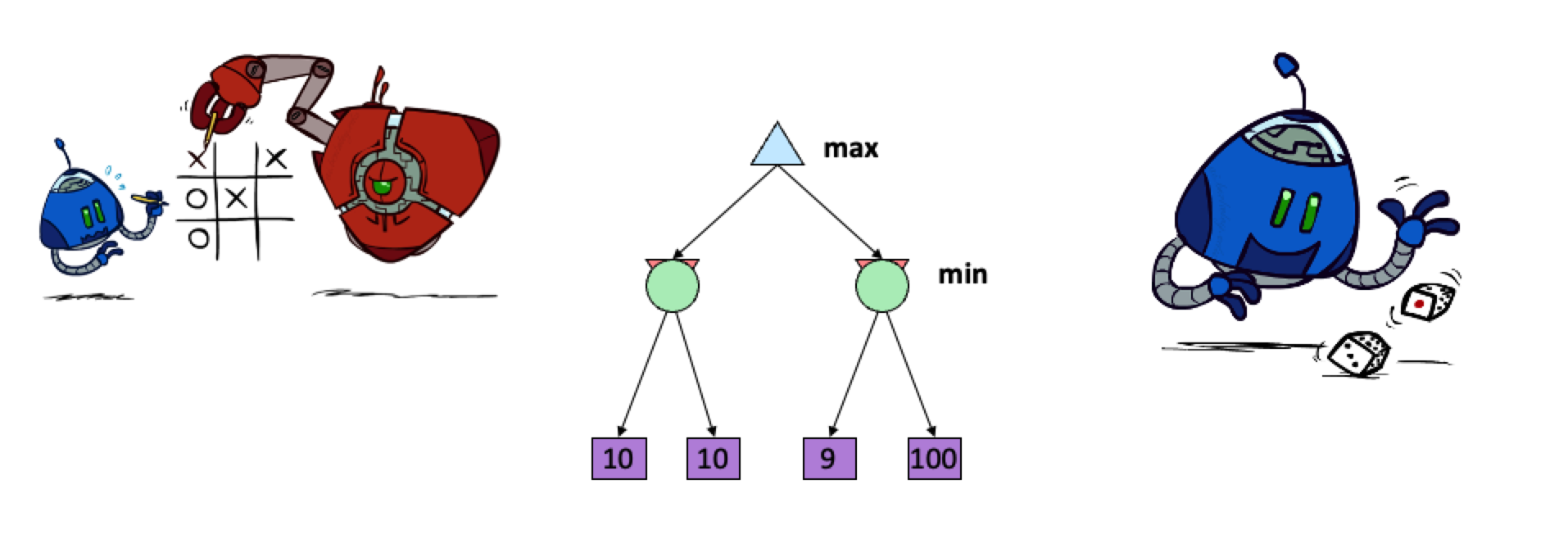
如上图所示，因此我们把中间层的倒三角替换成圆形了，圆形代表什么？其实圆形就是引入概率的、引入随机性的博弈。比如说两条边的概率都是0.5的话，右边的节点的值就是$\frac{1}{2}\cdot (9+100)$

由此，这颗搜索树从 Minmax Search 变成了 Expectimax Search。当我们考虑随机性的时候，就不去靠考虑最大值最小值了，而是考虑期望和均值。实际上，Expectimax在日常生活中很常见。比如说投色子，又比如说在pacman中鬼是随机游走的，不再是你死我亡型的鬼了。

计算

那么Expectimax Search是如何计算的？

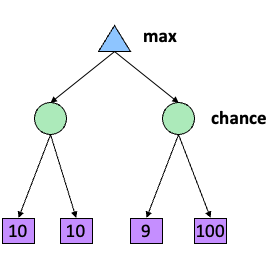
首先，对于chance节点，求的不再是最小值，而是 期望效用值。他和min的功能是一样的，只是结果是不确定的。

同时，max节点还是会计算chance节点的最大值，这和minimax search中的max节点功能一致

我们可以看一下Minimax search和 Expectimax search的区别

• Minimax Search

• Expectimax Search

伪代码

现在我们来看一下Expectimax Search的伪代码：

• value函数

def value(state):
    if the state is a terminal state: return the state’s utility
    # 子节点是max-value节点，那么调用max-value函数
    if the next agent is MAX: return max-value(state)
    # 子节点是exp-value节点，那么调用exp-value函数
    if the next agent is EXP: return exp-value(state)

• max-value函数, 这和minimax search的max节点是类似的

def max-value(state):
    initialize v = -∞
    for each successor of state:
    		v = max(v, value(successor))
    return v

• exp-value函数

def exp-value(state):
    initialize v = 0
    for each successor of state:
      # 由于chance节点的每条边都是由概率的，所以要先获取概率然后累加计算节点的值
        p = probability(successor)
    		v += p * value(successor)
    return v

Expectimax可以剪枝吗

首先，我们来看看不剪枝的情况下，Expectimax Search计算的一个例子：

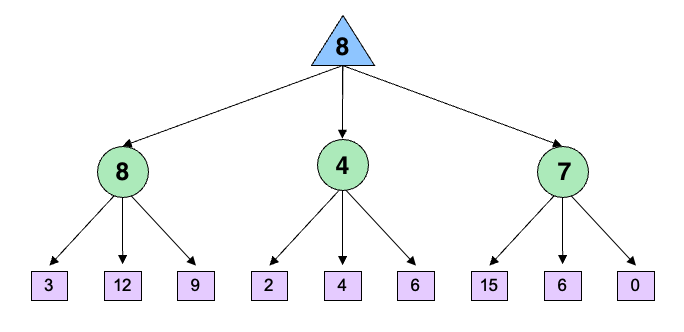
但是对于Expectimax来说，情况就变得很不一样了。假设我们遍历了最右边的子树，得到了其值为8，令$\alpha=8$，那么我们可以在遍历中间子树的第一个叶子(其值为2)之后就能对其进行剪枝吗？

显然是不行的，因为虽然每条边的概率是一样的，但是并不能确定叶子的值是多少，可能2后面的叶子是1亿，那么显然中间的chance节点的值是大于8的

因此Expectimax Search是不能做剪枝的，但如果在知道bound的情况下，还是可以做剪枝的。比如说，我知道2后面两个叶子的值都是小于10的，那么就可以做剪枝了

Expectimax 可以做限高吗

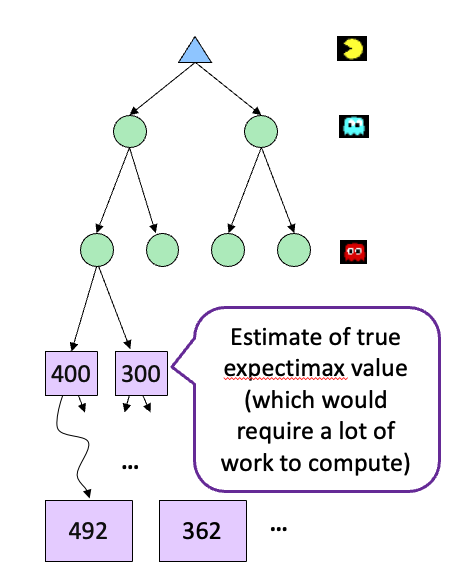
可以限高，但是比minimax更为复杂，因为其中涉及到概率相关的问题。

例题

在一个游戏中，如果对手在80%的时间里采用深度为2的minimax search，剩余20%的时间在随机游走，应该用什么？Expectimax Search

但这时候，chance节点的两条边的权重就不一样了。在80%的情况下，是求min的操作；在20%的情况下随机进行。通过这种方式去模拟可以求得针对该问题的概率值。但这种方法速度很慢，需要访问到最底部的叶子结点。

建模

在设计智能体的时候，常常会对日常生活做一个建模，两个极端的方向就是：过度乐观和过度悲观

• 乐观派是说，前面就算有鬼我也要走过去
• 悲观派是说， 前面就算是无害的小动物我也不敢走过去

我们用pacman为例：下面有四种情况，博弈的鬼和随机游走的鬼与Minimax和Expectimax两两搭配，我们来看一下结果是什么样的。

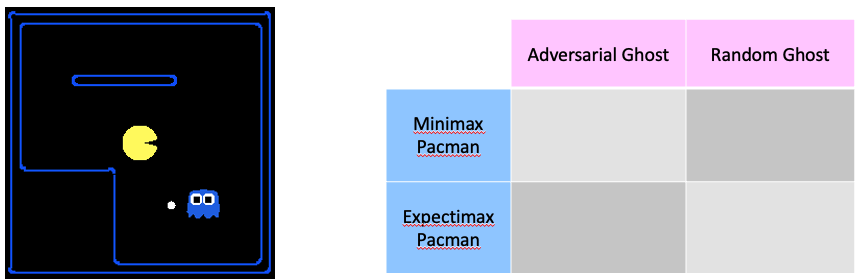
• Expectimax Pacman——Random Ghost

• Adversarial Ghost —— Minimax Pacman(对抗性的鬼和对抗性的pacman)

我们看到，因为鬼是对抗性的，所以一直在追着pacman跑，pacman则已知躲着鬼，然后吃到了果子

• Adversarial Ghost —— Expectimax Pacman(对抗性的鬼和Expectimax 的pacman)

我们看到鬼是Adversarial 的，非常具有攻击性。而pacman考虑了随机性后，有一定几率躲掉鬼，但不能保证每次都可以逃脱。视频中是赢了，但不一定下次还能赢。

• Random Gost——Minimax Pacman

我们看到在这种情况下，只要鬼还在地图的下半部分移动，上面的pacman就非常害怕不敢轻举妄动。因此，minimax其实是一种过度悲观的方式。

最后 我们来看一下，玩五次游戏以后，上面四种方式得到的分数：

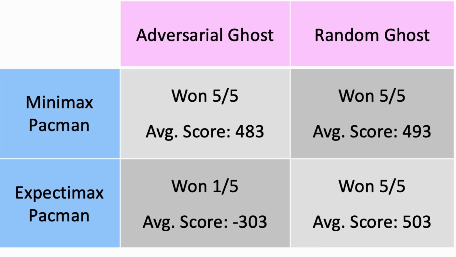
• 我们看到，Expectimax对上Random Gost五次都能赢，因为考虑了随机性
• Minimax对上Adversarial Ghost，由于Adversarial具有强烈的攻击性，而Minimax又是比较悲观的，因此他虽然赢了5次，但是平均得分不如Expectimax对上Random Ghost

• Expectimax对上Adversarial Ghost，我们看到只赢了一次，这是因为鬼具有强烈的攻击性，但是Pacman的行动却具有随机性，因此一着不慎就可能被鬼吃掉。

• MiniMax 对上Random Ghost，虽然小心翼翼地再走，但是最终还是能赢的