回溯剪枝整理

参考文献：https://labuladong.online/algo/practice-in-action/partition-to-k-equal-sum-subsets/#%E4%BB%A5%E6%A1%B6%E7%9A%84%E8%A7%86%E8%A7%92

这几天做了不少回溯的题目，虽然是暴力解法，但是其中涉及到球盒模型思维，如何高效剪枝的思维，都是很值得我们学习的。一些高效的剪枝操作，可以让代码的运行效率提高数十倍。因此所以我想整理一些常见的剪枝操作。

排序

1723. 完成所有工作的最短时间

这一道是困难题，第一思路是用二分搜索来求最小的最大，最大的最小这种。然后我将数组排序去用二分搜索的框架带入。但是这样是做不出来的。因为之前如这种1011. 在 D 天内送达包裹的能力题目中，都是必须按照给定的顺序来放到一个个桶中的，但在1723中并没有这个约束。

因此我还是选择暴力回溯。用球盒模型，每一个工人看做是一个桶，然后对于每一项工作，遍历桶，判断是否存放。

这里就遇到了第一个优化的点，就是排序，而且要逆序排列。为什么？这样较大的工作时间被先分配，可以更快地使得某个工人的工作时间达到较高值，从而更早地发现当前分配方案的最大工作时间是否已经超过当前最优解，从而提前剪枝，减少不必要的递归分支。

如果任务按照升序排列，那么在早期分支中，工人的工作时间累积得比较慢，可能需要更多任务才能超过最优解。这会导致必须深入递归后才能发现该分支无解，从而浪费了时间。而降序排序则能让无效分支在较浅层次就被剪除。

等效状态判断

还是1723这道题，仅仅排序也是不够的还需要进一步剪枝。这也是对这道题提升最大的地方。也就是等效状态判断。在这道题目中，工人没有顺序，因此先给哪位工人安排工作都是无所谓的。也就是说，选择第一个空桶后就可以直接跳出循环，不必再尝试其它空桶。

因此，我们在循环中，可以这样写

for(int i = 0;i<everyBodyTime.length;i++){
    //如何剪枝？
    if (everyBodyTime[i] + jobs[index] >= minTime) continue;
    // 剪枝：空桶剪枝。若该工人还未分配工作（空桶），那么只分配给第一个空桶即可
    if(everyBodyTime[i] == 0) {
        everyBodyTime[i] += jobs[index];
        traverse(jobs, everyBodyTime, index+1);
        everyBodyTime[i] -= jobs[index];
        break; // 直接 break，因为其他空桶产生的状态是对称的
    }


    everyBodyTime[i] += jobs[index];
    traverse(jobs,everyBodyTime,index+1);
    everyBodyTime[i] -= jobs[index];
}

关于等效状态判断，还有一题非常经典698. 划分为k个相等的子集这题是说给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。我们套入球盒模型，k个盒子，nums个球，从球的角度出发，遍历k个盒子，判断是否要放入。在这里，k个盒子没有先后顺序之分，因此也需要用等效状态来剪枝。具体来说，当我们对每个数字尝试放入不同的桶时，会出现这样的情况：如果两个桶当前的和是相同的，那么把当前数字放入这两个桶其实会产生“对称”的状态，也就是说，它们得到的结果是等价的。

例如，假设 bucket[0] 和 bucket[1] 当前都为 5，并且目标值是 10，当我们尝试将当前数字 3 放入这两个桶时：

如果放入 bucket[0]，则 bucket[0] 变为 8，bucket[1] 仍然为 5；
如果放入 bucket[1]，则 bucket[1] 变为 8，bucket[0] 仍然为 5。

这两种状态在后续递归中所探索的可能性是等价的，只不过桶的顺序不同，但对于问题本身没有影响。

因此，我们可以这样写回溯函数：

public void traverse(int[] nums,int[] bucket,int index,int target){
    if(index == nums.length){
        boolean current = true;
        for(int b:bucket){
            if(b!=target) current = false;
        }
        if(current) flag = true;
        return;
    }

    for(int i = 0;i<bucket.length;i++){
        int num = nums[index];
      //重点：剪枝等效状态
        if(i > 0 && bucket[i] == bucket[i-1]){
            continue;
        }
        if(bucket[i] + num > target) continue;
        bucket[i] += num;
        traverse(nums,bucket,index+1,target);
        bucket[i] -= num;
    }
}

这两种剪枝是可以互换的，效率不会差太多。第二种减去的情况多一些，效率会略好一些。

2305. 公平分发饼干这题也可以用这种剪枝来快速提高效率，本质上都是一道题目

状态存储

还是698. 划分为k个相等的子集这题，我们不妨从盒的角度出发，用每一个盒去装球，如果装满了，那么就装下一个盒子，一直到所有盒子都装满。

但是效率很低，我们可以思考一下是否还有优化的空间。

首先，在这个解法中每个桶都可以认为是没有差异的，但是我们的回溯算法却会对它们区别对待，这里就会出现重复计算的情况。

什么意思呢？我们的回溯算法，说到底就是穷举所有可能的组合，然后看是否能找出和为 target 的 k 个桶（子集）。

那么，比如下面这种情况，target = 5，算法会在第一个桶里面装 1, 4：

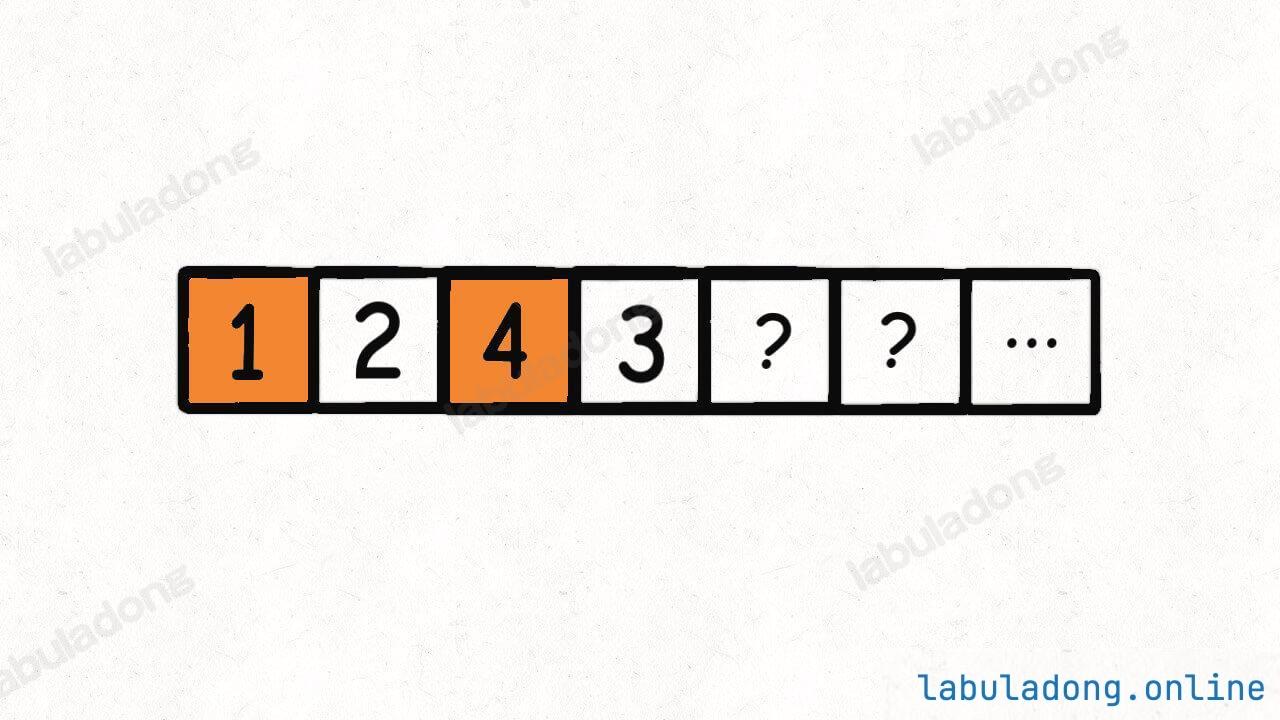
现在第一个桶装满了，就开始装第二个桶，算法会装入 2, 3：

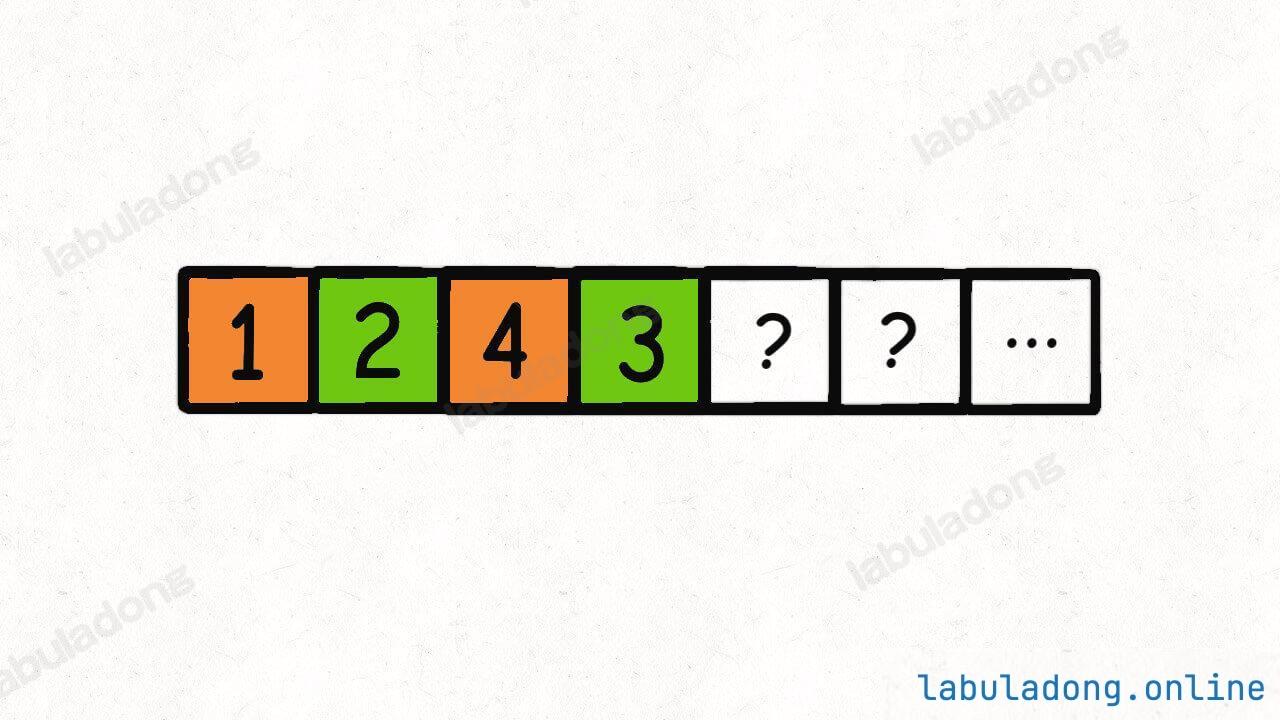
然后以此类推，对后面的元素进行穷举，凑出若干个和为 5 的桶（子集）。

但问题是，如果最后发现无法凑出和为 target 的 k 个子集，算法会怎么做？

回溯算法会回溯到第一个桶，重新开始穷举，现在它知道第一个桶里装 1, 4 是不可行的，它会尝试把 2, 3 装到第一个桶里：

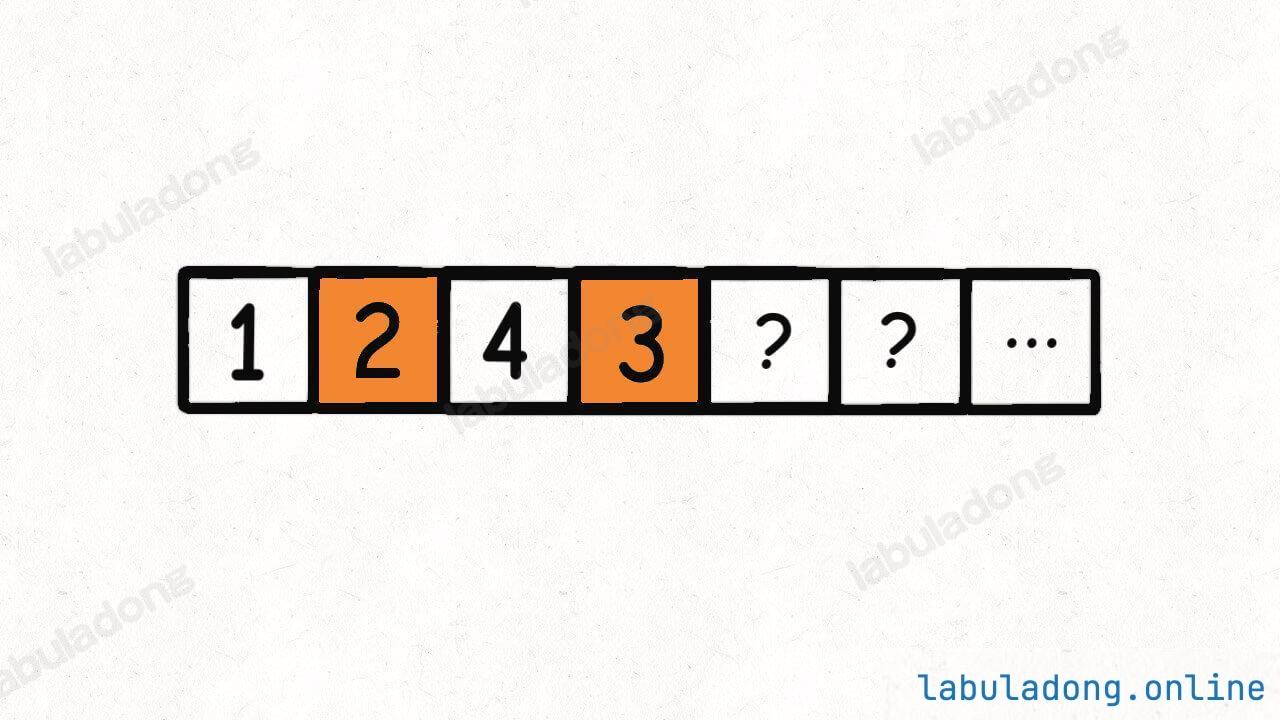
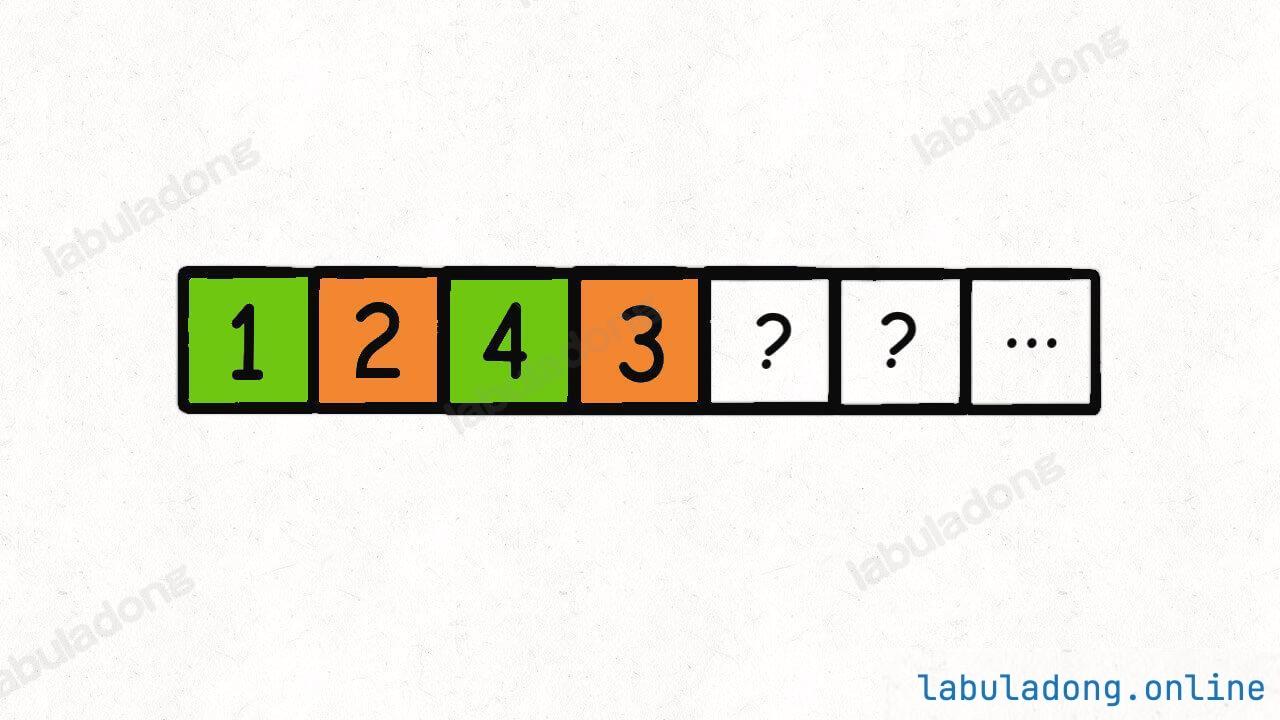
好，到这里你应该看出来问题了，这种情况其实和之前的那种情况是一样的。也就是说，到这里你其实已经知道不需要再穷举了，必然凑不出来和为 target 的 k 个子集。

但我们的算法还是会傻乎乎地继续穷举，因为在她看来，第一个桶和第二个桶里面装的元素不一样，那这就是两种不一样的情况呀。

那么我们怎么让算法的智商提高，识别出这种情况，避免冗余计算呢？

你注意这两种情况的 used 数组肯定长得一样，所以 used 数组可以认为是回溯过程中的「状态」。

所以，我们可以用一个 memo 备忘录，在装满一个桶时记录当前 used 的状态，如果当前 used 的状态是曾经出现过的，那就不用再继续穷举，从而起到剪枝避免冗余计算的作用。

有读者肯定会问，used 是一个布尔数组，怎么作为键进行存储呢？这其实是小问题，比如我们可以把数组转化成字符串，这样就可以作为哈希表的键进行存储了。

class Solution {

    // 备忘录，存储 used 数组的状态
    HashMap<String, Boolean> memo = new HashMap<>();

    public boolean canPartitionKSubsets(int[] nums, int k) {
        // 见上文
    }

    boolean backtrack(int k, int bucket, int[] nums, int start, boolean[] used, int target) {        
        // base case
        if (k == 0) {
            return true;
        }
        // 将 used 的状态转化成形如 [true, false, ...] 的字符串
        // 便于存入 HashMap
        String state = Arrays.toString(used);

        if (bucket == target) {
            // 装满了当前桶，递归穷举下一个桶的选择
            boolean res = backtrack(k - 1, 0, nums, 0, used, target);
            // 将当前状态和结果存入备忘录
            memo.put(state, res);
            return res;
        }
        
        if (memo.containsKey(state)) {
            // 如果当前状态曾今计算过，就直接返回，不要再递归穷举了
            return memo.get(state);
        }

        // 其他逻辑不变...
      for(....)
    }
}

其实我认为，状态存储和上一届判断状态是否一致，是等价的，都是减去不必要的重复状态的计算。