BST

知识点概述

二叉查找树(Binary Search Tree, BST), 又称为二叉搜索树，二叉排序树，是一种对查找和排序都有用的特殊二叉树。

二叉查找树或是空树，或是满足如下性质的二叉树：

1) 若其左子树非空，则左子树上所有结点的值均小于根结点的值

2) 若其右子树非空，则右子树上所有结点的值均大于等于根结点的值

3) 其左右子树本身又各是一棵二叉查找树。
二叉查找树的特性：左子树＜根<右子树即二叉查找树的中序遍历是一个递增序列

一般来说节点是不能相等的，如果硬要相等的话可以引入计数器

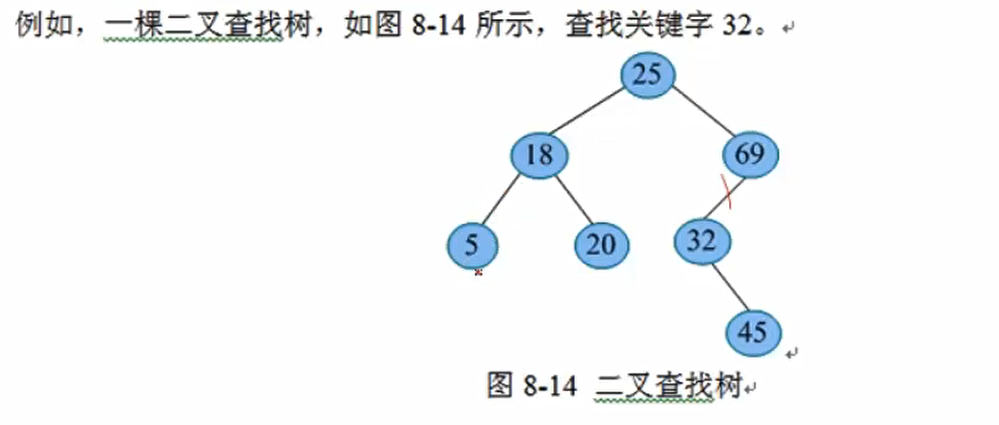
二叉查找树的查找

因为二叉查找树的中序遍历有序性，所以查找和二分查找类似，每次缩小查找范围，查找的效率较高。

算法步骤：

1) 若二叉查找树为空，查找失败，返回空指针
2) 若二叉查找树非空，将待查找关键字 x 与根结点的关键字 T->data 比较：

若 x==T->data, 查找成功，返回根结点指针
若 x\< T->data, 则递归查找左子树
若 x> T->data, 则递归查找右子树

代码实现

BSTree SearchBST(BSTree T,ElemType key)//二叉排序树的递归查找
{
    //若查找成功，则返回指向该数据元素结点的指针，否则返回空指针
    if((!T)|| key==T->data)
        return T;
    else if (key<T->data)
            return SearchBST(T->lchild,key);//在左子树中继续查找
        else
            return SearchBST(T->rchild,key); //在右子树中继续查找
}

算法分析

时间复杂度

二叉查找树的查找时间复杂度和树的形态有关，可分为最好情况、最坏情况和平均情况分析。

最好情况下，二叉查找树的形态和二分查找的判定树相似，如图8-18所示。每次查找可以缩小—半的搜索范围，查找路径最多从根到叶子，比较次数最多为树的高度$O(\log n)$ 最好情况的平均查找长度为$O(\log n)$

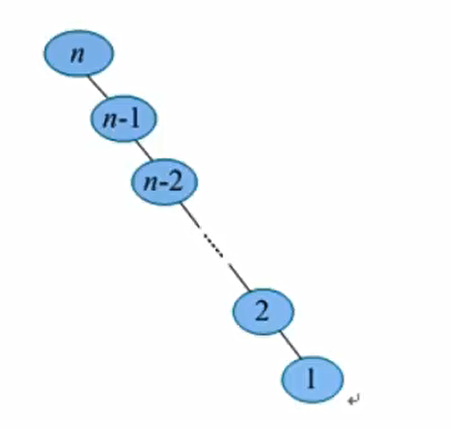
最坏情况下，二叉排序树的形态为单支树，即只有左子树或只有右子树。每次查找的搜索范围缩小为n-1，退化为顺序查找，最坏情况的平均查找的长度为$O(n)$

n个结点的二叉查找树有n!颗（有的形态相同），可以证明，平均情况下，二叉查找树的平均查找长度也为$O(\log n)$

空间复杂度

空间复杂度为 O(1)

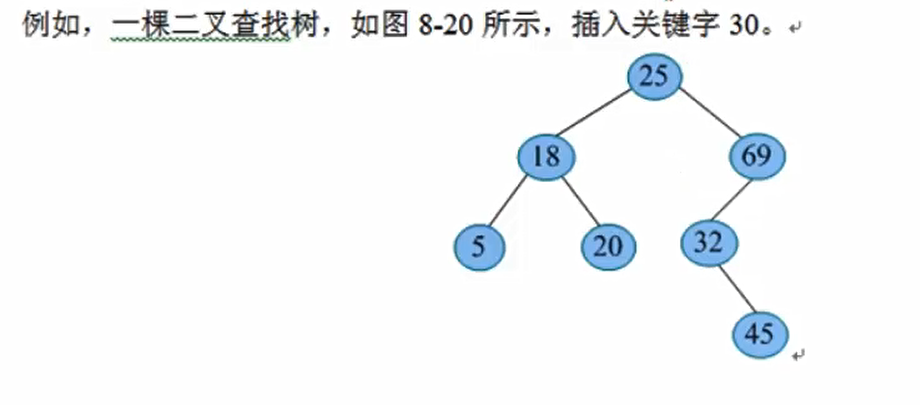
二叉搜索树的插入

因为二叉查找树的中序遍历有序性，首先要查找待插入关键字的插入位置，当查找不成功时，将待插入关键字作为新的叶子结点插入到最后一个查找结点的左孩子或右孩子。

算法步骤

1) 若二叉查找树为空，创建一个新的结点 S, 将待插入关键字放入新结点的数据域，s结点作为根节点，左右子树均为空。如果查找成功，要么什么也不做，要么设置一个变量记录出现次数

2) 若二叉查找树非空，将待查找关键字x与根节点的关键字 T->data比较：

若x\< T->data,则将x插入到左子树
若x>T->data, 则将x插入到右子树

代码实现

void InsertBST(BSTree &T,ElemType e)//二叉排序树的插入
{
    //当二叉排序树T中不存在关键字等于e的数据元素时，则插入该元素
    if(!T)//如果T是空的，说明这个位置就是我们要插入的位置
    {
        BSTree S=new BSTNode; //生成新结点
        S->data=e;             //新结点S的数据域置为e
        S->lchild=S->rchild=NULL;//新结点S作为叶子结点
        T=S;            		//把新结点S链接到已找到的插入位置
    }
    else if(e<T->data)
            InsertBST(T->lchild,e );//插入左子树
        else if(e>T->data)
            InsertBST(T->rchild,e);//插入右子树
}

算法分析：

二叉查找树的插入需要线查找插入位置，插入本身只需要常数时间，但查找插入位置的时间复杂度为$O(\log n)$

二叉查找树的创建

二叉查找树的创建可以从空树开始，按照输入关键字的顺序依次进行插入操作，最终得到一棵二叉查找树

算法步骤

1) 初始化二叉查找树为空树，T=NULL

2) 输入一个关键字x，将x插入到二叉查找树T当中

3) 重复步骤2），直到关键字输入完毕

算法实现

void CreateBST(BSTree &T )//二叉排序树的创建
{
    //依次读入一个关键字为key的结点，将此结点插入二叉排序树T中
    T=NULL;
    ElemType e;
    cin>>e;
    while(e!=ENDFLAG)//ENDFLAG为自定义常量，作为输入结束标志
    {
        InsertBST(T,e);  //插入二叉排序树T中
        cin>>e;
    }
}

算法分析

二叉查找树的创建，需要n次插入，每次需要$O(\log n) $时间 ,因此创建二叉搜索树的时间复杂度为$O(n\log n)$

相当于把一个无序序列转换为一个有序序列的排序过程。实际上，创建二叉查找树的过程和快速排序一样。根节点相当于快速排序中的基准元素，左右两部分划分的情况取决于基准元素，创建二叉查找树的时候，输入序列的次序不同，创建的二叉查找树是不同的

二叉查找树的删除

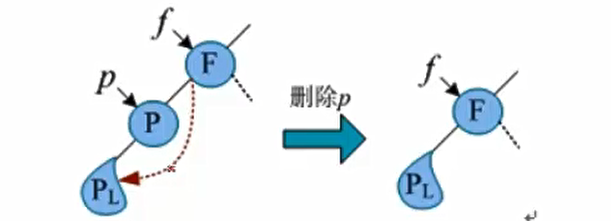
首先要在二叉查找树中找到待删除的结点，然后执行删除操作。假设指针p指向待删除的结点，指针f指向p的双亲结点。根据待删除结点所在的位置不同，删除操作处理方法也不同可以分为3种情况

被删除节点右子树为空

如果被删除节点右子树为空，则令其左子树子承父业代替其位置即可。例如，在二叉查找树中删除p结点，如图所示

被删除节点左右子树均不空

如果被删除结点的左子树和右子树均不空，则没办法再使用子承父业的方法了。根据二叉查找树的中序有序性，删除该结点时，可以用其直接前驱（或直接后继）代替其位置，然后删除其直接前驱（或直接后继）即可。那么中序遍历序列中，一个结点的直接前驱（或直接后继）是哪个结点呢?

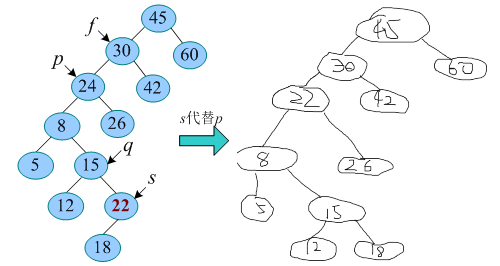
直接前驱：中序遍历中，结点p的直接前驱为其左子树的最右结点。即沿着p的左子树一直访问其右子树，直到没有右子树，就找到了最右结点。如图下图a所示。 s 指向p的直接前驱，q指向s的双亲。

直接后继：中序遍历中，结点p的直接后继为其右子树的最左结点。如图上图b所示s指向p的后继，q指向s的双亲

例如，在二叉查找树之中删除24，首先查找到24的位置p，然后找到p的直接前驱s(22)结点，令22赋值给p的数据域，删除s结点，删除过程如图

特殊情况

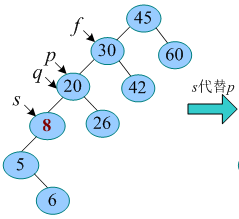
特殊情况就是左右子树都非空，但是左子树并没有右子树。那么cl直接接到q的左子树上

比如这里我想删除20，

举例

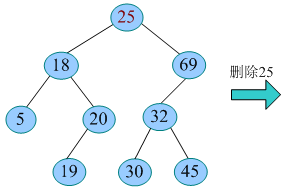
用最大前驱来代替

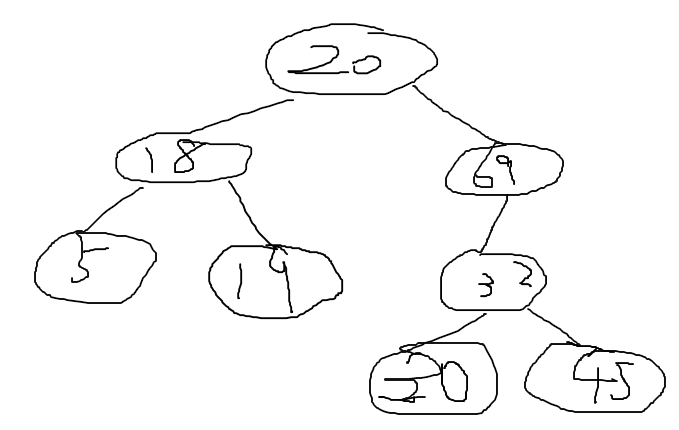
或者用最小后继来代替

算法步骤：

1) 在二叉查找树中查找待删除关键字的位置，p指向待删除结点， f指向p的双亲结点(f一开始为空)，如果查找失败，则返回。

2) 如果查找成功，则分三种情况进行删除操作：

如果被删除结点左子树为空，则令其右子树子承父业代替其位置即可。
如果被删除结点右子树为空，则令其左子树子承父业代替其位置即可。
如果被删除结点右子树均不空，则令其互接前驱（或互接后继）代替之，再删除其互接前驱（或互接后继）

代码一览

#include<iostream>
using namespace std;
#define ENDFLAG -1
typedef int ElemType;

typedef struct BSTNode{
	ElemType data;	//结点数据域
	BSTNode *lchild,*rchild;	//左右孩子指针
}BSTNode,*BSTree;

BSTree SearchBST(BSTree T,ElemType key)//二叉排序树的递归查找
{
    //若查找成功，则返回指向该数据元素结点的指针，否则返回空指针
    if((!T)|| key==T->data)
        return T;
    else if (key<T->data)
            return SearchBST(T->lchild,key);//在左子树中继续查找
        else
            return SearchBST(T->rchild,key); //在右子树中继续查找
}

void InsertBST(BSTree &T,ElemType e)//二叉排序树的插入
{
    //当二叉排序树T中不存在关键字等于e的数据元素时，则插入该元素
    if(!T)
    {
        BSTree S=new BSTNode; //生成新结点
        S->data=e;             //新结点S的数据域置为e
        S->lchild=S->rchild=NULL;//新结点S作为叶子结点
        T=S;            		//把新结点S链接到已找到的插入位置
    }
    else if(e<T->data)
            InsertBST(T->lchild,e );//插入左子树
        else if(e>T->data)
            InsertBST(T->rchild,e);//插入右子树
}

void CreateBST(BSTree &T )//二叉排序树的创建
{
    //依次读入一个关键字为key的结点，将此结点插入二叉排序树T中
    T=NULL;
    ElemType e;
    cin>>e;
    while(e!=ENDFLAG)//ENDFLAG为自定义常量，作为输入结束标志
    {
        InsertBST(T,e);  //插入二叉排序树T中
        cin>>e;
    }
}

void DeleteBST(BSTree &T,char key)
{
  //从二叉排序树T中删除关键字等于key的结点
    /*
    一开始p指向T，f指向p的父亲，也就是NULL
    */
    BSTree p=T;BSTree f=NULL;
    BSTree q;
    BSTree s;
    if(!T) return; //树为空则返回
    while(p)//查找
    {
        if(p->data==key) break;  //找到关键字等于key的结点p，结束循环
        f=p;                //f为p的双亲，因为接下来p会变成他的左右孩子
        if (p->data>key)
            p=p->lchild; //在p的左子树中继续查找
        else
            p=p->rchild; //在p的右子树中继续查找
    }
    if(!p) return; //找不到被删结点则返回
    
    //三种情况：p左右子树均不空、无右子树、无左子树
    if((p->lchild)&&(p->rchild))//被删结点p左右子树均不空
    {
        q=p;//让q指向p，s去找p的左子树的最右结点
        s=p->lchild;
        while(s->rchild)//在p的左子树中继续查找其前驱结点，即最右下结点
        {
            q=s;
            s=s->rchild;
        }
        p->data=s->data;  //s的值赋值给被删结点p,然后删除s结点
        if(q!=p)		 //q!=p说明 q向p的左子树的右子树方向移动了
            q->rchild=s->lchild; //把s的左子树赋值给q的右子树
        else			//否则说明 q仍然是p的左子树，就是上面说的特殊情况
            q->lchild=s->lchild; //把s的左子树赋值给q的左子树
        delete s;
    }
    else
    {
        if(!p->rchild)//被删结点p无右子树，只需重接其左子树
        {
            q=p;
            p=p->lchild;
        }
        else if(!p->lchild)//被删结点p无左子树，只需重接其右子树
        {
             q=p;
             p=p->rchild;
        }
/*――――――――――将p所指的子树挂接到其双亲结点f相应的位置――重连――――――*/
        if(!f)
            T=p;  //被删结点为根结点，那么令p为根节点。
        else if(q==f->lchild)
                f->lchild=p; //挂接到f的左子树位置
            else
                f->rchild=p;//挂接到f的右子树位置
        delete q;
	}
}

void InOrderTraverse(BSTree &T)//中序遍历
{
    if(T)
	{
        InOrderTraverse(T->lchild);
        cout<<T->data<<"\t";
        InOrderTraverse(T->rchild);
	}
}

int main()
{
	BSTree T;
	cout<<"请输入一些整型数，-1结束"<<endl;
	CreateBST(T);
	cout<<"当前有序二叉树中序遍历结果为"<<endl;
	InOrderTraverse(T);
	cout<<endl;
	ElemType key;//待查找或待删除内容
	cout<<"请输入待查找关键字"<<endl;
	cin>>key;
	BSTree result=SearchBST(T,key);
	if(result)
        cout<<"找到"<<key<<endl;
	else
        cout<<"未找到"<<key<<endl;
	cout<<"请输入待删除关键字"<<endl;
	cin>>key;
	DeleteBST(T,key);
	cout<<"当前有序二叉树中序遍历结果为"<<endl;
	InOrderTraverse(T);
	return 0;
}

AVL平衡二叉树

平衡二叉查找树 (Balanced Binary Search Tree, BBST), 简称平衡二叉树，由前苏联数学家 Adelson-Velskii和 Landis 提出，所以又称为 AVL 树。

平衡二叉树或者为空树，或者为具有以下性质的平衡二叉树：

1) 左右子树高度差的绝对值不超过 1;

2) 左右子树也是平衡二叉树。

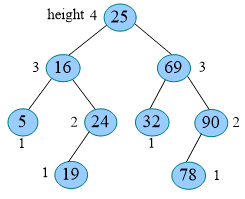
结点左右子树的高度只差称为平衡因子。二叉查找树中，每个结点的平衡因子绝对值不超过1即为平衡二叉树。例如，一颗平衡二叉树及其平衡因子

那么在这棵平衡二叉树中插入20, 结果会怎样？如图8-46所示。插入20之后，从该叶子到树根路径上的所有结点，平衡因子都有可能改变，出现不平衡，有可能有多个结点平衡因子绝对值超过1。从新插入结点向上找离新插入结点最近的不平衡结点，以该结点为根的子树称为最小不平衡子树。只需要将最小不平衡子树调整为平衡二叉树即可，其它结点不变。

平衡二叉树除了适度平衡性，还具有局部性：

1) 单次插入、删除后，至多有 $O(1)$处出现不平衡

2) 总可以在 $O(logn)$时间内，使这 $ O(1)$处不平衡重新调整为平衡。

平衡二叉树在动态修改后出现的不平衡，只需要局部（最小不平衡子树）调平衡即可，不需要整棵树调整。

在任意一颗非空平衡二叉树T1中，删除某节点v之后形成的平衡二叉树$T_2$ ，再将v插入$T_2$ 形成平衡二叉树 T3, 那么：取v为T1中的任意节点，T1和T3都可能相同可能不同

平衡二叉树的调整

那么如何局部调平衡呢？

调整平衡的方法
以插入操作为例，调整平衡可以分为四种情况: LL型、 RR型、 LR型、 RL型。

LL型

插入新结点C后，从该结点向上找到最近的不平衡结点A, 如果最近不平衡结点到新结点的路径前两个都是左子树 L, 即为 LL 型。也就是说，C结点插入在A的左子树的左子树中， A的左子树因插入新结点高度增加，造成A的平衡因子由1增为2, 失去平衡。需要进行 LL 旋转（顺时针）调整平衡。

每一次旋转，总有一个子树被抛弃，一个指针空闲，它们正好配对。旋转之后，是否平衡呢

旋转之后， A、B两个结点的左右子树高度之差均为0, 满足平衡条件， C的左右子树未变，仍然平衡。

代码

T指向最小不平衡子树的根。temp指向其左子树。

把temp的右子树（被抛弃的孩子）过继给T当左孩子

temp的右子树指向T，完成旋转

然后要更新T子树的高度和temp子树的高度

返回新树根

AVLTree LL_Rotation(AVLTree &T)//LL旋转
{
    AVLTree temp=T->lchild;
    T->lchild=temp->rchild;
    temp->rchild=T;
    updateHeight(T);//更新高度
    updateHeight(temp);
    return temp;
}

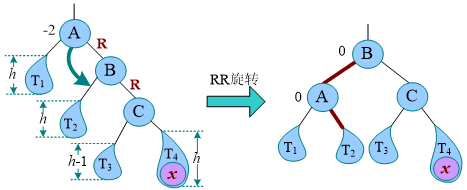
RR 型

插入新结点x后，从该节点向上找到最近的不平衡节点A，如果最近不平衡节点到新节点的路径前两个都是右子树R，即为RR型。需要进行RR旋转(逆时针)调整平衡

AVLTree RR_Rotation(AVLTree &T)//RR旋转
{
    AVLTree temp=T->rchild;
    T->rchild=temp->lchild;
    temp->lchild=T;
    updateHeight(T);//更新高度
    updateHeight(temp);
    return temp;
}

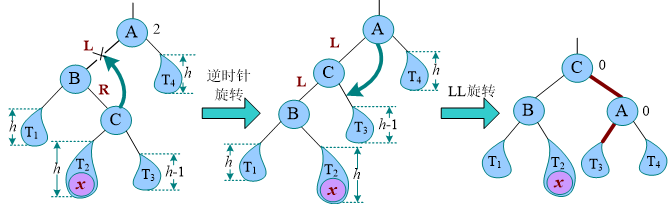
LR 型

插入新节点x后，从该结点向上找到最近的不平衡节点A，如果最近不平和给结点到新节点的路径前两个一次是左子树L和右子树R，即为LR型

旋转一次之后，变成了LL型，那么就进行LL旋转即可

或者让B转过来。

AVLTree LR_Rotation(AVLTree &T)//LR旋转
{
     T->lchild=RR_Rotation(T->lchild);
     return LL_Rotation(T);
}

RL型

插入新结点x后，从该结点向上找到最近的不平衡结点A, 如果最近不平衡结点到新结点的路径前依次时右子树R、左子树L, 即为RL型。

AVLTree RL_Rotation(AVLTree &T)//RL旋转
{
    T->rchild=LL_Rotation(T->rchild);
    return RR_Rotation(T);
}

平衡二叉树的插入

在平衡二叉树上插入新的数据元素 X, 首先查找其插入位置，查找过程中，用p指针记录当前结点， J指针记录p的双亲，其算法描述如下。

算法步骤

1) 在平衡二叉树查找 X, 如果查找成功，则什么也不做，返回p; 如果查找失败，则执行的插入操作；
2) 创建一个新结点p存储 X, 该结点的双亲为f, 高度为1。
3) 从新结点之父J出发，向上寻找最近的不平衡结点。逐层检查各代祖先结点，如果平衡，则更新其高度，继续向上寻找，如果不平衡，则判断失衡类型（沿着高度大的子树判断，刚插入新结点的子树必然高度大），并作相应的调整，返回p。

例如，我们在这棵树中插入20，那么这样24的平衡因子是2，需要调整了

因为是LR型，我们先把20逆时针移到19和24之间，然后把24顺时针旋转，作为20的右子树

AVLTree Insert(AVLTree &T,int x)
{
    if(T==NULL) //如果为空，创建新结点
    {
        T=new AVLNode;
        T->lchild=T->rchild=NULL;
        T->data=x;
        T->height=1;
        return T;
     }
    if(T->data==x) return T;//查找成功，什么也不做，查找失败时才插入
    if(x<T->data)//插入到左子树
    {
        T->lchild=Insert(T->lchild,x);//注意插入后饭后结果挂接到T->lchild
        if(Height(T->lchild)-Height(T->rchild)==2)
 //插入后看是否平衡，如果不平衡显然是插入的那一边高度大。插入到左子树，左子树肯定比右子树高
        {                                         //沿着高度大的那条路径判断
            if(x<T->lchild->data)//判断是LL还是LR,即插入的是lchild节点的lchild 还是rchild
                T=LL_Rotation(T);
            else
                T=LR_Rotation(T);
        }
    }
    else//插入到右子树
    {
        T->rchild=Insert(T->rchild,x);
        if(Height(T->rchild)-Height(T->lchild)==2)
        {
            if(x>T->rchild->data)
                T=RR_Rotation(T);
            else
                T=RL_Rotation(T);
        }
    }
    updateHeight(T);
    return T;
}

平衡二叉树的创建

平衡二叉树的创建和二叉查找树的创建类似，只是插入操作多了调平衡而已。可以丛空树开始，按照输入关键字的顺序依次进行插入操作，最终得到一颗平衡二叉树

算法步骤：

初始化平衡二叉树为空树，T=NULL;
输入一个关键字x，将x插入到平衡二叉树T中
重复步骤2，直到关键字输入完毕

代码

AVLTree CreateAVL(AVLTree &T)
{
    int n,x;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>x;
        T=Insert(T,x);
    }
    return T;
}

平衡二叉树的删除

插入只需要从插入结点之父向上检查，发现不平衡立即调整，一次调平横即可。

删除操作则需要一直从删除节点之父向上检查，发现不平衡立即调整，然后继续向上检查，检查到树根为止

算法步骤：

在平衡二叉树查找 X,如果查找失败，则返回，如果查找成功，则执行删除操作（回二叉查找树的删除）
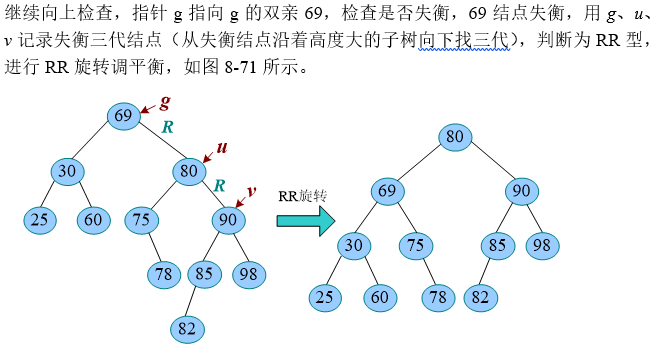
从实际被删除结点之父g出发（当被删结点有左右子树时，令其直接前驱（或直接后继）代替其位置，删除其直接前驱，实际被删结点为其直接前驱（或直接后继）），向上寻找最近的不平衡结点。逐层检查各代祖先结点，如果平衡，则更新其高度，继续向上寻找，如果不平衡，则判断失衡类型（沿着高度大的子树判断），并作相应的调整。
继续向上检查，一直到树根

AVLTree Delete(AVLTree &T,int x)
{
    if(T==NULL) return NULL;
    if(T->data==x)//如果找到删除节点
    {
        if(T->rchild==NULL)
  //如果该节点的右孩子为NULL,那么直接删除.如果左右都空，那么就返回NULL
        {
            AVLTree temp=T;
            T=T->lchild;
            delete temp;
        }
        else//否则，将其右子树的最左孩子作为这个节点（直接后继），并且递归删除这个节点的值
        {
           AVLTree temp;
           temp=T->rchild;
           while(temp->lchild)
              temp=temp->lchild;
           T->data=temp->data;
           T->rchild=Delete(T->rchild,T->data);
           updateHeight(T);
        }
        return T;
    }

    if(T->data>x)//调节删除节点后可能涉及的节点
        T->lchild=Delete(T->lchild,x);
    if(T->data<x)
        T->rchild=Delete(T->rchild,x);
    updateHeight(T);//更新T的高度
    if(T->lchild)//如果有左子树，那么调整左子树，是调平衡用的
        T->lchild=adjust(T->lchild);
    if(T->rchild)
        T->rchild=adjust(T->rchild);
    if(T) T=adjust(T);
    return T;
}
AVLTree adjust(AVLTree &T)//删除结点后，需要判断是否还是平衡，如果不平衡，就要调整
{
    if(T==NULL) return NULL;
    if(Height(T->lchild)-Height(T->rchild)==2)//沿着高度大的那条路径判断
    {
        if(Height(T->lchild->lchild)>=Height(T->lchild->rchild))
            T=LL_Rotation(T);
        else
            T=LR_Rotation(T);
    }
    if(Height(T->rchild)-Height(T->lchild)==2)//沿着高度大的那条路径判断
    {
        if(Height(T->rchild->rchild)>=Height(T->rchild->lchild))
            T=RR_Rotation(T);
        else
            T=RL_Rotation(T);
    }
    updateHeight(T);
    return T;
}

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

typedef struct AVLNode{
   int data;
   int height;
   struct AVLNode *lchild;
   struct AVLNode *rchild;
}*AVLTree;

AVLTree Empty(AVLTree &T)//删除树
{
    if(T==NULL) return NULL;
    Empty(T->lchild);
    Empty(T->rchild);
    delete T;
    return NULL;
}

inline int Height(AVLTree T)//计算高度
{
    if(T==NULL) return 0;
    return T->height;
}

void updateHeight(AVLTree &T)
{
     T->height=max(Height(T->lchild),Height(T->rchild))+1;
}

AVLTree LL_Rotation(AVLTree &T)//LL旋转
{
    AVLTree temp=T->lchild;
    T->lchild=temp->rchild;
    temp->rchild=T;
    updateHeight(T);//更新高度
    updateHeight(temp);
    return temp;
}

AVLTree RR_Rotation(AVLTree &T)//RR旋转
{
    AVLTree temp=T->rchild;
    T->rchild=temp->lchild;
    temp->lchild=T;
    updateHeight(T);//更新高度
    updateHeight(temp);
    return temp;
}

AVLTree LR_Rotation(AVLTree &T)//LR旋转
{
     T->lchild=RR_Rotation(T->lchild);
     return LL_Rotation(T);
}

AVLTree RL_Rotation(AVLTree &T)//RL旋转
{
    T->rchild=LL_Rotation(T->rchild);
    return RR_Rotation(T);
}

AVLTree Insert(AVLTree &T,int x)
{
    if(T==NULL) //如果为空，创建新结点
    {
        T=new AVLNode;
        T->lchild=T->rchild=NULL;
        T->data=x;
        T->height=1;
        return T;
     }
    if(T->data==x) return T;//查找成功，什么也不做，查找失败时才插入
    if(x<T->data)//插入到左子树
    {
        T->lchild=Insert(T->lchild,x);//注意插入后饭后结果挂接到T->lchild
        if(Height(T->lchild)-Height(T->rchild)==2)//插入后看是否平衡，如果不平衡显然是插入的那一边高度大
        {                                         //沿着高度大的那条路径判断
            if(x<T->lchild->data)//判断是LL还是LR,即插入的是lchild节点的lchild 还是rchild
                T=LL_Rotation(T);
            else
                T=LR_Rotation(T);
        }
    }
    else//插入到右子树
    {
        T->rchild=Insert(T->rchild,x);
        if(Height(T->rchild)-Height(T->lchild)==2)
        {
            if(x>T->rchild->data)
                T=RR_Rotation(T);
            else
                T=RL_Rotation(T);
        }
    }
    updateHeight(T);
    return T;
}

AVLTree adjust(AVLTree &T)//删除结点后，需要判断是否还是平衡，如果不平衡，就要调整
{
    if(T==NULL) return NULL;
    if(Height(T->lchild)-Height(T->rchild)==2)//沿着高度大的那条路径判断
    {
        if(Height(T->lchild->lchild)>=Height(T->lchild->rchild))
            T=LL_Rotation(T);
        else
            T=LR_Rotation(T);
    }
    if(Height(T->rchild)-Height(T->lchild)==2)//沿着高度大的那条路径判断
    {
        if(Height(T->rchild->rchild)>=Height(T->rchild->lchild))
            T=RR_Rotation(T);
        else
            T=RL_Rotation(T);
    }
    updateHeight(T);
    return T;
}

AVLTree Delete(AVLTree &T,int x)
{
    if(T==NULL) return NULL;
    if(T->data==x)//如果找到删除节点
    {
        if(T->rchild==NULL)//如果该节点的右孩子为NULL,那么直接删除
        {
            AVLTree temp=T;
            T=T->lchild;
            delete temp;
        }
        else//否则，将其右子树的最左孩子作为这个节点，并且递归删除这个节点的值
        {
           AVLTree temp;
           temp=T->rchild;
           while(temp->lchild)
              temp=temp->lchild;
           T->data=temp->data;
           T->rchild=Delete(T->rchild,T->data);
           updateHeight(T);
        }
        return T;
    }

    if(T->data>x)//调节删除节点后可能涉及的节点
        T->lchild=Delete(T->lchild,x);
    if(T->data<x)
        T->rchild=Delete(T->rchild,x);
    updateHeight(T);
    if(T->lchild)
        T->lchild=adjust(T->lchild);
    if(T->rchild)
        T->rchild=adjust(T->rchild);
    if(T) T=adjust(T);
    return T;
}

void Preorder(AVLTree T)//前序遍历方便看树的结果
{
    if(T==NULL) return ;
    cout<<T->data<<"\t"<<T->height<<endl;
    Preorder(T->lchild);
    Preorder(T->rchild);
}

 void Inorder(AVLTree T)//中序遍历方便看树的结果
{
    if(T==NULL) return ;
    Inorder(T->lchild);
    cout<<T->data<<"\t"<<T->height<<endl;
    Inorder(T->rchild);
}

 void Posorder(AVLTree T)//后序遍历方便看树的结果
{
    if(T==NULL) return ;
    Posorder(T->lchild);
    Posorder(T->rchild);
    cout<<T->data<<"\t"<<T->height<<endl;
}

void show(AVLTree T)
{
    Preorder(T);
    cout<<endl;
    Inorder(T);
    cout<<endl;
    Posorder(T);
}

AVLTree CreateAVL(AVLTree &T)
{
    int n,x;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>x;
        T=Insert(T,x);
    }
    return T;
}
int main()
{
    int x;
    AVLTree root=NULL;
    root=Empty(root);
    CreateAVL(root);
    show(root);
    cin>>x;
    root=Delete(root,x);
    show(root);
    return 0;
}