一阶微分方程

可分离变量微分方程

右边可以分成一个关于x的函数和一个关于y的函数相乘，比如$ x^2 y$ ；$x^2+y^2 $这样的就不能算这类型的函数

对第一个式子进行变形我们得到了第二个式子，这也是可分离的

最后把y放在一起，x放在一起， 求解

分离变量方程的解法

例一

例二

例三

例四

例五

C的范围一定要给出，C为任意常数

小结

解可分离变量的微分方程的步骤：

1. 根据题目给出的方程化为 $\frac{dy}{dx} = f(x)g(y)$ 类型的式子
2. 再变形，得到 $\frac{dy}{g(y)} = dxf(x)$ 类型的式子。x归一边，y 归一边
3. 两边同时求积分，$\int \frac{dy}{g(y)} = \int f(x)dx +C$
4. 最后得到答案，记住，不要忘记加上C！

齐次方程

注意点

1. 分类讨论。如果题目中带有根号，在同除x或y的时候需要判断其是否大于0，并更改对应的符号

1. 要注意常数和C的不同

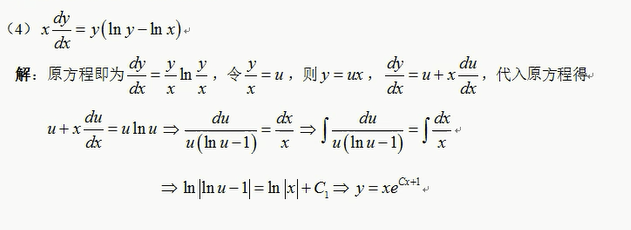
可化为齐次方程的方程

一阶线性微分方程

一阶线性微分方程的标准形式：$\frac{dy}{dx} + P(x)y = Q(x)$

若 $Q(x)\equiv 0$ 称为齐次方程

若 $Q(x)\not \equiv 0$ 称为非齐次方程

齐次方程：

1. 解齐次方程 $\frac{dy}{dx} + P(x)y = 0$
2. 分离变量 $\frac{dy}{y} = -P(x)dx$
3. 两边积分 $ln|y| = -\int P(x)dx+ln|C|$
4. 故通解为 $y = Ce^{-\int P(x)dx}$

非齐次方程：

我们需要用到很有用的方法： 常数变易法。也就是先求出非齐次方程对应的齐次方程的通解。再令式中的C为$u(x)$,将其变为函数
也就是 作变换 $y(x) = u(x)e^{-\int P(x)dx}$

然后再带入非齐次方程，作为它的一个解。

所以原非齐次方程可以变成：

$u’e^{-\int P(x)dx}-P(x)ue^{-\int P(x)dx}+P(x)ue^{-\int P(x)dx} = Q(x)$

即 $\frac{du}{dx} = Q(x)e^{\int P(x)dx}$

两端积分可得： $u = \int Q(x)e^{\int P(x)dx}dx+C$ 注意，这个C不能忘记！

原齐次方程方程的通解： $y =u(x)e^{-\int P(x)dx} = e^{-\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+C]$

例一

例二

伯努利方程

伯努利方程的标准形式：

$\frac{dy}{dx} +P(x)y = Q(x)y^n(n\neq0,1)$

方法：

1. 首先标出 P(x),Q(x) 分别是多少！
2. 令 $z=y^{1-n}$, 则 $\frac{dz}{dx} = (1-n)y^{-n} \frac{dy}{dx}$
3. 带入原伯努利方程得到： $\frac{dz}{dx} + (1-n)P(x)z = (1-n)Q(x)$ , 也就是我们熟悉的线性方程。然后求其次、设u(x) 等步骤

求出这个z和x的线性方程之后，我们再把 $z=y^{1-n}$ 带入得到伯努利方程的通解。

例题4

小结

1. 一阶线性方程 $\frac{dy}{dx}+P(x)y = Q(x)$

方法： 先解齐次方程，再用常数变易法

要注意：可以转换为 $\frac{dx}{dy}$ 那么接下来就是x，y都反一下就可以了。

1. 伯努利方程 $\frac{dy}{dx} +P(x)y = Q(x)y^n,(n\neq 0,1)$

方法： 令 $u = y^{1-n}$ 转化为线性方程求解

全微分方程

我们拿到微分方程，可以先判断一下他是不是全微分方程。全微分方程属于难度较低的一类。

一阶微分方程可以写成 $P(x,y)dx+Q(x,y)dy = 0$ 的形式，若他的左边恰好是某个函数 $u(x,y)$ 的全微分， 即
$du(x,y) = P(x,y)dx+Q(x,y)$ 则称 上式为全微分方程

方程 $P(x,y)dx+Q(x,y)dy = 0$ 等同于 $du(x,y) = 0$ 由此可知，全微分方程(1) 的通解是方程 $u(x,y) = C$ 所确定的隐函数。

$P(x,y)dx+Q(x,y)dy = 0$ 是全微分的充要条件为： $\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x }$

而且满足方程1 的原函数可以由曲线积分 $u(x,y) = \int{x_0}^xP(x,y_0)dx+\int{y_0}^yQ(x,y)dy$ 求得，其中$(x_0,y_0)$为定义域D中任意选定的点。

这里要注意了，如果x，y再分数里，那么要判断 $x_0,y_0$ 是否可以取0 ，如果不能取0就取1

例题1

求微分方程 $(2x+e^{y^2})dx+(2xye^{y^2}-2y)dy = 0$ 的通解

例题2

求解 $(x+\frac{y}{x^2})dx-\frac{1}{x}dy=0$

那么我们可以想到，如果一个方程不是全微分，我们可以通过一个乘以一个积分因子，将其变为全微分的形式。

现在引入积分因子的概念

积分因子

例题3

分项组合是求积分因子的有效方法。常见的积分因子有:

$d(xy) = ydx+xdy$

$d(\frac{y}{x})= \frac{xdy-ydx}{x^2}$

$d(arctan\frac{y}{x})=\frac{xdy-ydx}{x^2+y^2}$

$d(ln(x+y))= \frac{dx+dy}{x+y}$

$d(ln(x^2+y^2))= \frac{2xdx+2ydy}{x^2+y^2}$

$d(\frac{1}{y}) = \frac{1}{y^2}$

练习： 解方程 $2xy^3dx+(x^2y^2-1)dy = 0$

$y^2(2xydx+x^2)dy-dy = 0$

$x^2y+\frac{1}{y}=C$