离散数学之图1

Graphs

边集E就是顶点V和V的笛卡尔集中的子集。笛卡尔集是每连个点之间都有连线(包括自环)。
对一些图我们需要有基本的概念
- V和G可能是无限的,理论上存在,现实中可能是不会存在的
- 在一幅图中,每一条边连接的是不同的两个顶点,没有两条边连接的是同一对顶点。那么这个就是个简单图
- 排除自环 和 两个顶点有相同方向的两条边
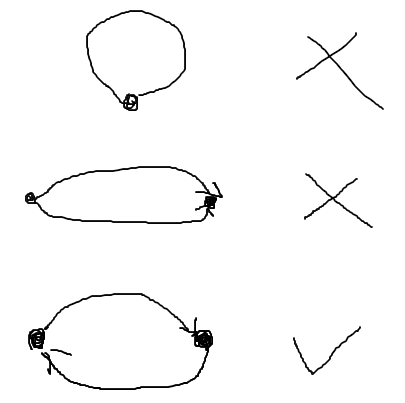
- 否则,我们允许上面的情况,那么这就是个多图
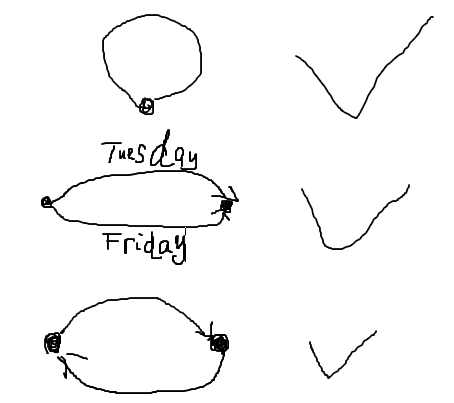
- 比如说我们礼拜二和礼拜五都会去健身,这样可以画两条边,从家里到健身房。但是简单图之是去过健身房这个关系就建立了。
- 如果有一条自己到自己的边,那么就叫做环
Directed graphs

比如说我关注了一个大V但是它没有关注我,所以这就是单向的。如果大V关注了我,那么就有两条不同方向的边。
graph terminology
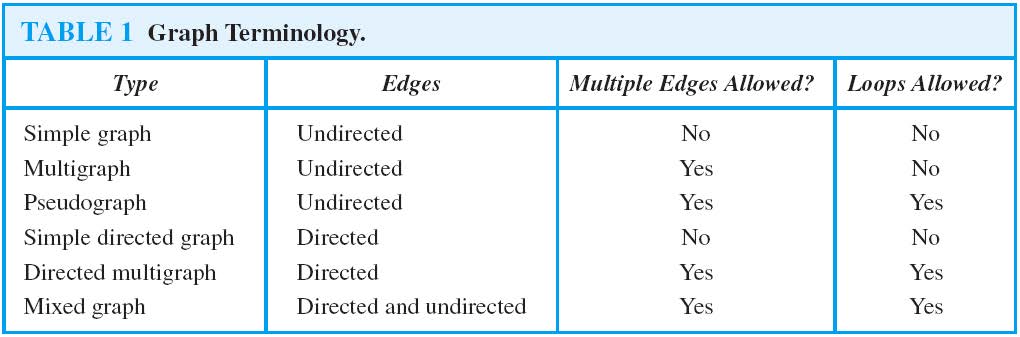
- 如果是无向图,$(u,v)\in E => (v,u)\in E$ 所以无向图可以看成双向图
Graph Models
model1 Social networks

model2 Communication networks

交互的网络,比如说我和谁联系。或者我转发了某人的微博。是以传播信息为目的的
model3 Information networks

信息网络。比如专利、论文之间的引用关系。专利、观点、论文之间也有引用的关系。
又比如超链接在网页中的嵌入。
model4 Software design applications

软件设计里的应用。我们可以描述不同模块之间的 关系是什么。比如我执行软件在后台的逻辑。这里面的逻辑调用了什么模块。基于这样的网络可以分析软件的内核是什么。
在执行的时候语句也构成了一个网络
model5 Transportation networks

比如说交通网络。基于这样一个图我们可以分析世界航运中心在哪里。
或者我们可以根据这个路网制作导航。
model6 Biological networks

这是一个生物信息的网络。
Graph Terminology
Basic concepts for undirected graphs
Neighbors

在无向图里,uv相连接,u是v的邻居,v是u的邻居
Neighborhood

我们可以把所有的邻居都找出来。这就是一个v的社区
Degree

一个顶点的度就是连接到这个顶点的边的数量
对于简单图来说。$deg(v) = |N(v)|$
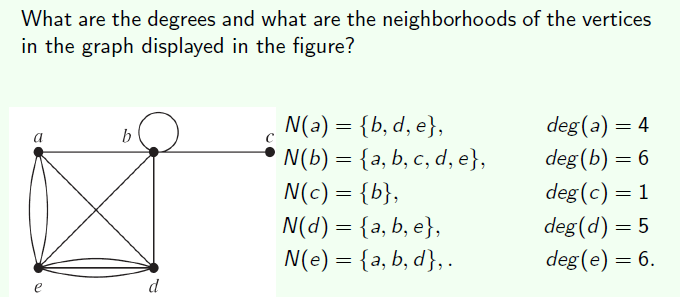
- 这里有一个无向图。a这个顶点的neibor有 b、d、e 连接的边有4条。所以deg(a) = 4
- 这不是一个简单图,否则deg(a) = N(v)
- 对于 b,neighbor a,b,c,d,e 因为有自环,且在无向图里,所以度要加2;在有向图中加1即可
握手定理
所有结点的度之和为什么是两倍的边的数量?
因为我同一条边会在一对结点中计算两次
据此可以推论 :在无向图(包括简单图)中,degree是奇数的顶点的个数一定是偶数个。但这只是一个必要条件,度为奇数的顶点数量为偶数个并不能说明一定可以画处一个简单图,甚至连图都可能画不出。比如度为 5 5 4 3 2 1 的6个顶点,就画不出一个图

Basic concepts for directed graphs
有向图中具有方向 $(u,v)\in E$ 那么 有一条以u为起点,v为终点,u指向v的边
但是这里度要分为出度和入度
Adjacent

Degree

Degrees on directed graphs
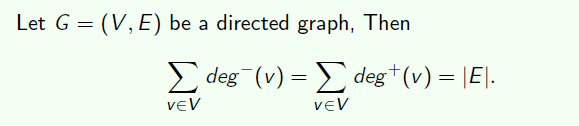
在有向图中,出度等于入度等于边的数量
比如:
- 如果有自环,那么在这个结点中的入度+1,出度+1
- 孤立点不指向任何点,也没有进来的边,出度入度都为0
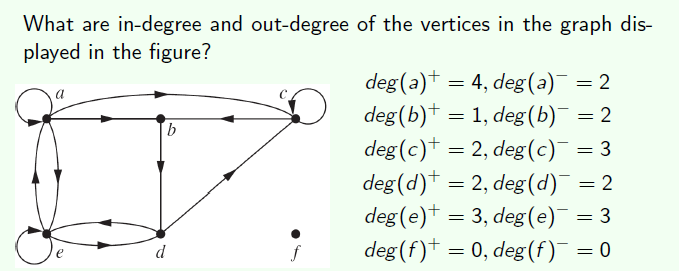
Special Types of Graphs
Complete graphs
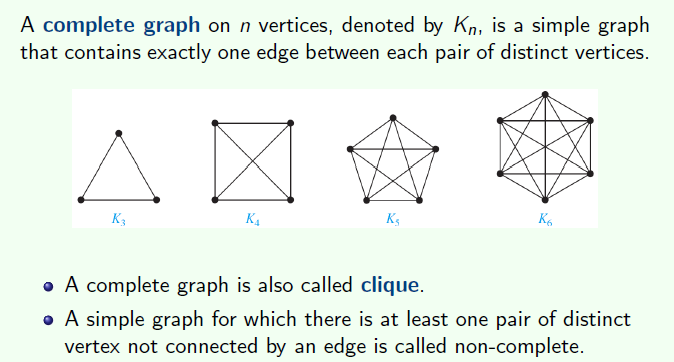
完全图就是每两个顶点之间都有一条边,但没有多边,没有自环。是一个简单图
只要少一条边,就不再是一个完全图了
Cycles and wheels
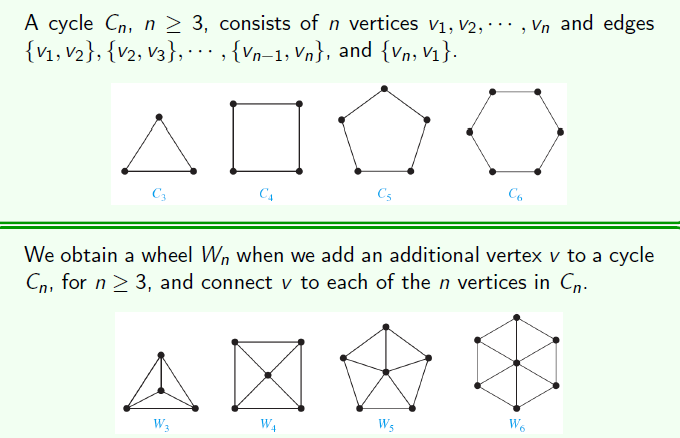
轮图,和轮子一样。外面每一个顶点都是3,里面的顶点的度取决于边数
n-Cubes

Bipartite graphs
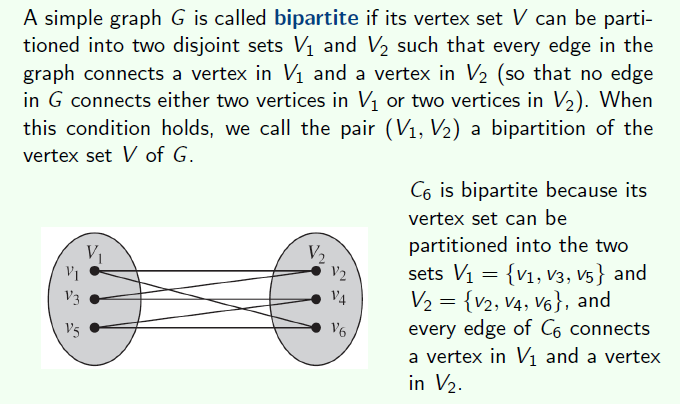
二部图或者说是二分图。他是一个简单图。但是定点可以分成两部分v1,v2
边一定是包含在 $V_1*V_2$的笛卡尔集里面。所以不会出现 $V_1-V_1$这种的边
比如我们去看电影,一边是观众一边是电影
还可以有三步图,四步图……
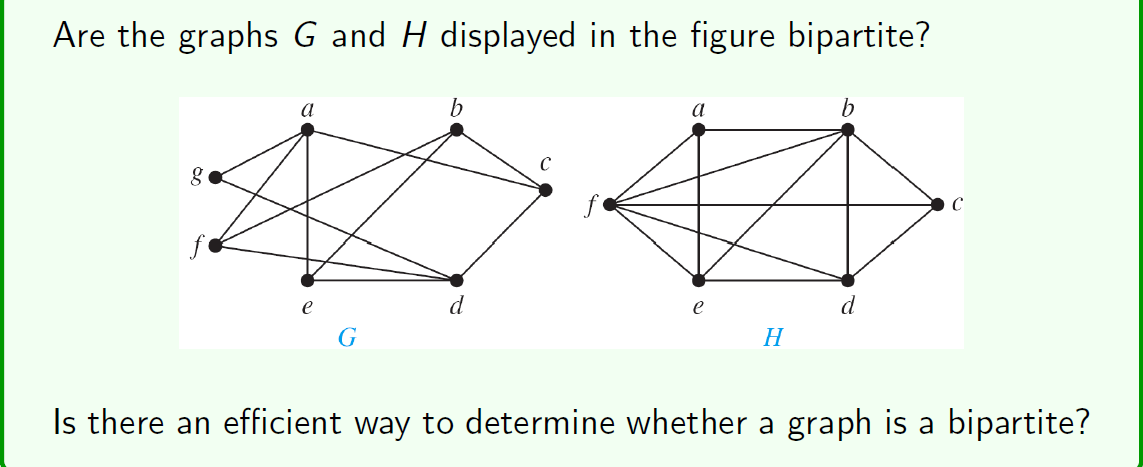
A simple graph is bipartite if and only if it is possible to assign one of two different colors to each vertex of the graph so that no two adjacent vertices are assigned the same color.
也就是说,因为相连的两个顶点必然不可能在同一个集合当中,所以我们可以给他们涂上不同的颜色。再来看看整张图中是否存在两个颜色相同的点相连的状况。如果有的话那这就不是一个二分图。

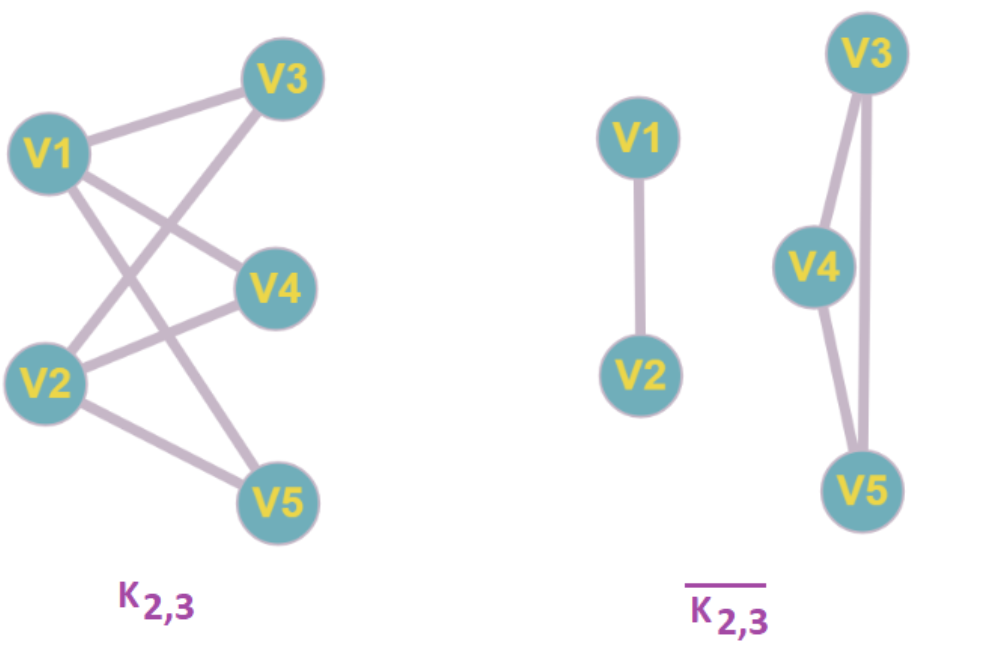
Complete bipartite graphs
A complete bipartite graph $K_{m,n}$ is a graph that has its vertex set partitioned into two subsets of m and n vertices, respectively with an edge between two vertices if and only if one vertex is in the first subset and the other vertex is in the second subset.
也就是说
完全二分图是一种特殊的二分图,可以把图中的顶点分成两个集合,使得第一个集合中的所有顶点都与第二个集合中的所有顶点相连。
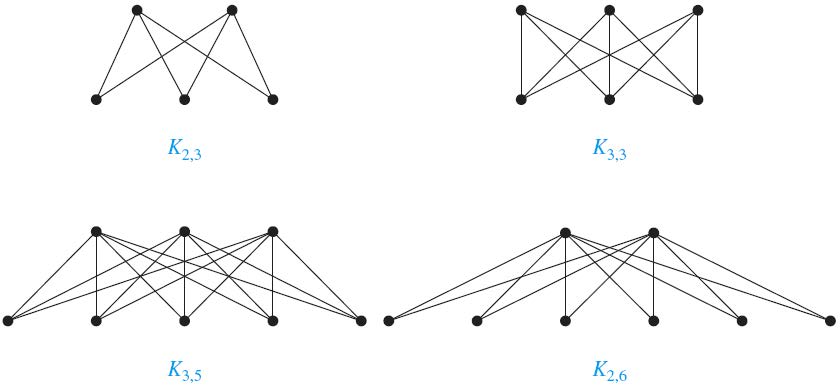
不同图的节点数和边数
| 图的类型 | 节点数 | 边数 |
|---|---|---|
| $K_n$ | $n$ | $\frac{(n-1)n}{2}$ |
| $C_n$ | $n$ | $n$ |
| $W_n$ | $n+1$ | $2n$ |
| $K_{m,n}$ | $m+n$ | $m\cdot n$ |
| $Q_n$ | $2^n$ | $n\cdot2^{n-1}$ |
Matching 匹配
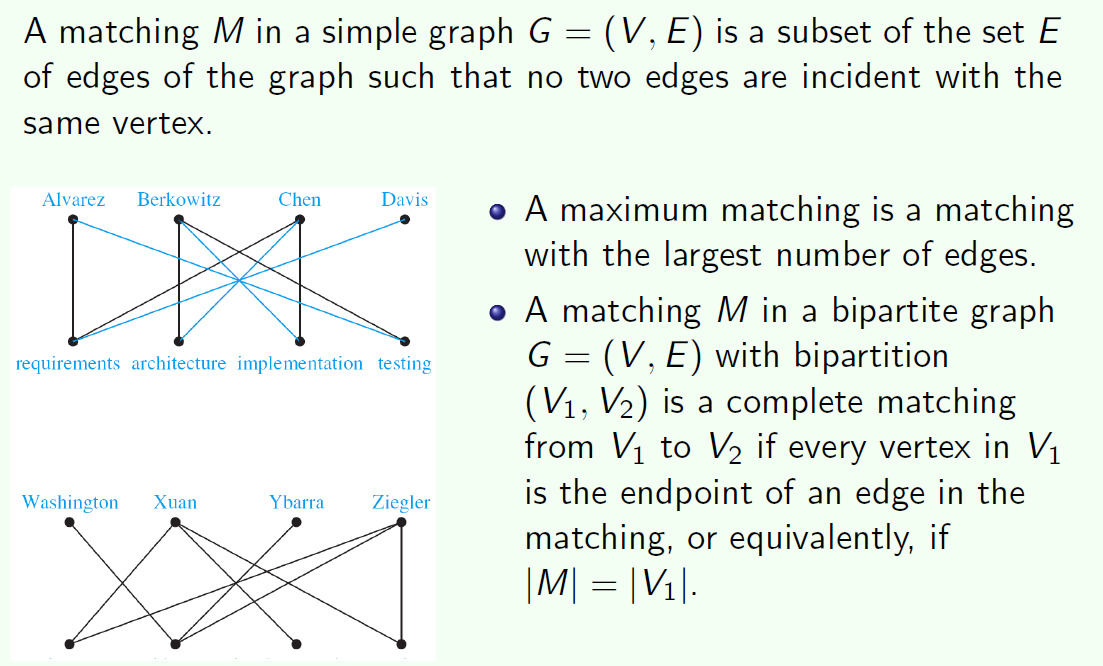
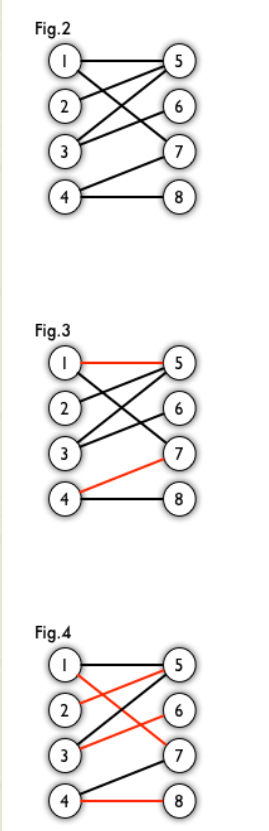
在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完全匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完全匹配。图 4 是一个完全匹配。显然,完全匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完全匹配。
(选自博客https://blog.csdn.net/qq_36345036/article/details/76977294)
Hall’S Marriage theorem
Theorem
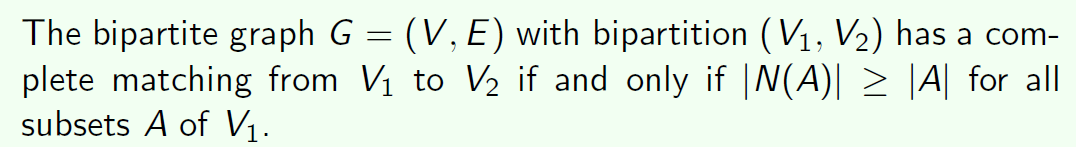
对于一个二分图G={X+Y,E} ,它满足:
∀W⊆X,$|W|≤|N_G(W)|$ ⟺ X中的每个结点都有匹配.
其中$N_G(W)$为图G中所有与W相连的结点的集合。
由这个定理,我们能得到一个推论:
二分图G的最大匹配M等于$|X|−max(|W|−|N_G(W)|)$
二分图有完全匹配当且仅当 $|N(A)|\geq|A|$ ,其中$A$代表了$V_1$当中的所有子集(包括空集)。 |N(A)| 代表了集合A中的所有元素的邻居的个数。|A| 代表了 子集中元素的个数,$N(\emptyset)$ = $\emptyset$, $|N(\emptyset)| = |\emptyset| = 0$
比如这张图来说,有没有一个完全匹配呢?
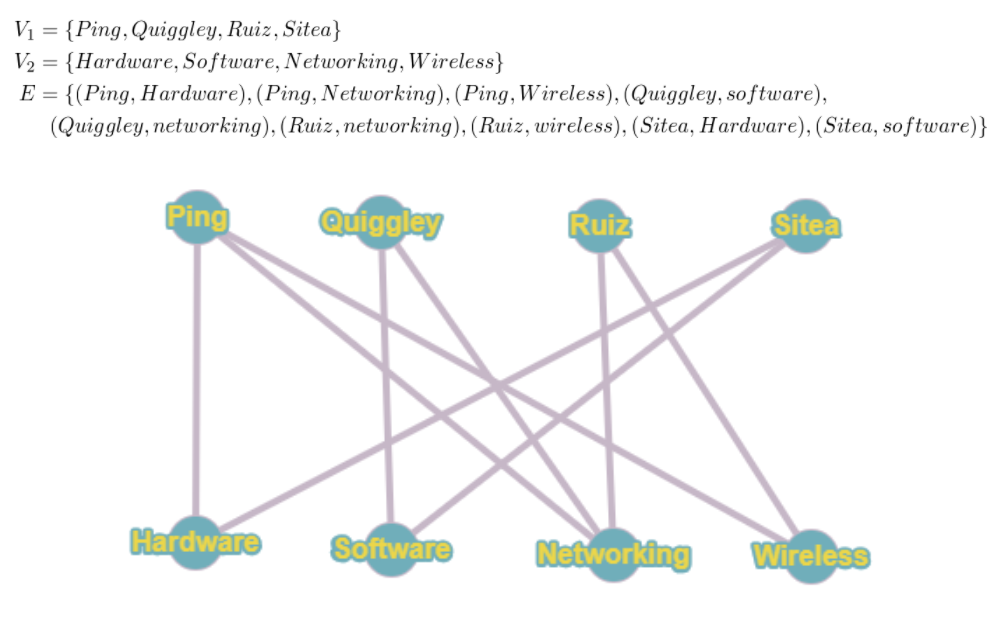


由Hall’s 定律,这张图是有完全匹配的
proof



New Graphs from Old
Subgraph 子图

Remove or adding edges of a graph

Edge contractions and vertices remove

Graph union
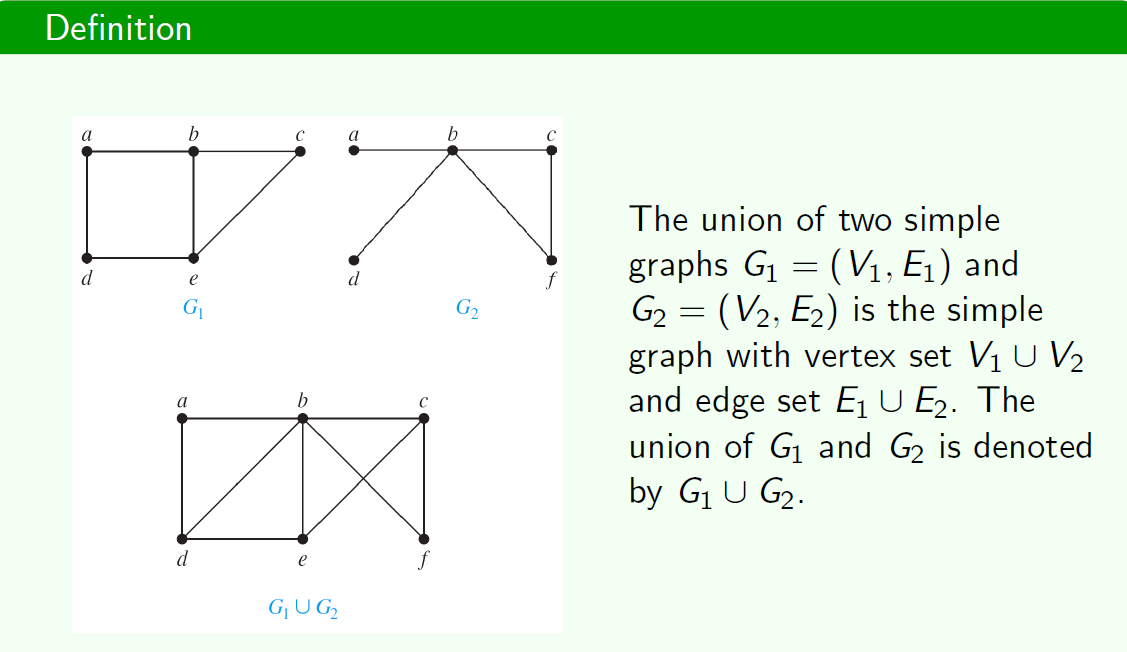
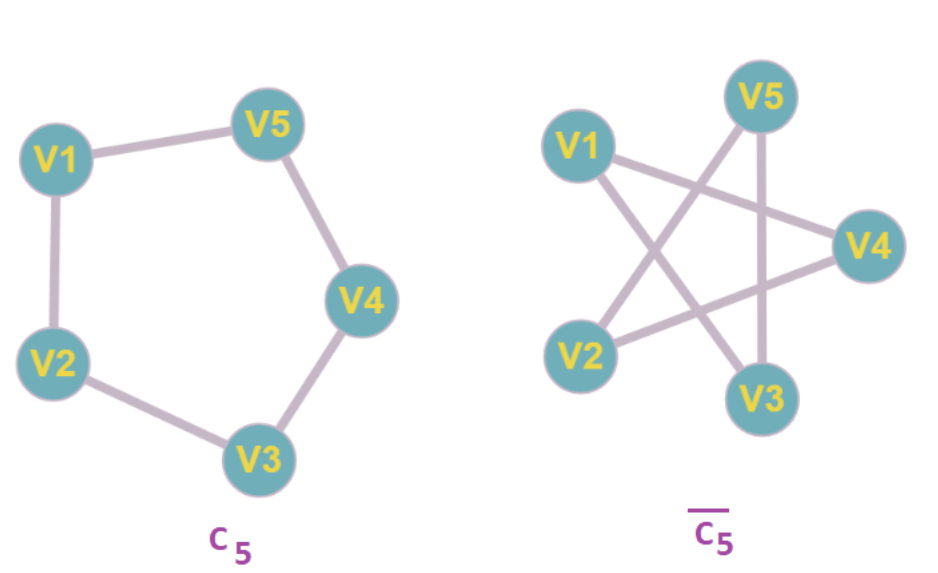
$\overline G$ 和G 的区别
$\overline G$ of a simple graph G has the same vertices as G, Two vertices are adjacent in $\overline G$ if and only if they are not adjacent in G.
也就是说在$\overline G$ 当中,G中不连在一起的点连在一起,连在一起的点现在不连在一起。