图与贪心算法
最短路径:Dijkstra算法
给定有向图带权图 G= (V, E), 其中每条边的权是非负实数。此外,给定V中的—个顶点,称为源点。现在要计算从源点到所有其他各顶点的最短路径长度, 这里路径长度指路上各边的权之和。
如何求其他各顶点的最短路径呢?
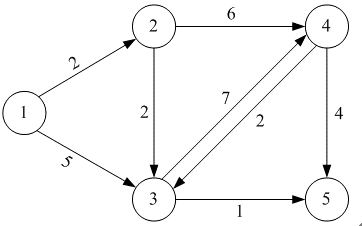
1->2 的最短路径为2
1->3的最短路径是2+2 = 4
……
迪科斯彻提出了著名的单源最短路径求解算法——Dijkstra算法。艾兹格• W• 迪科斯彻(Edsger Wybe Dijkstra), 荷兰人, 计算机科学家。 他早年钻研物理及数学, 后转而研究计算学今 他曾在1972年获得过素有 “计算机科学界的诺贝尔奖” 之称的图灵奖, 与Donald Ervin Knuth并称为我们这个时代最伟大的计算机科学家。
Dijkstra算法是解决单源最短路径问题的贪心算法, 它先求出长度最短的—条路径, 再参照该最短路径求出长度次短的—条路径, 直到求出从源点到其他各个顶点的最短路径。
Dijkstra算法的基本思想是首先假定源点为u, 顶点集合V被划分为两部分:集合S和V-S 。 初始时S中仅含有源点u, 其中S中的顶点到源点的最短路径已经确定。 集合V-S 中所包含的顶点到源点的最短路径的长度待定, 称从源点出发只经过S中的点到达V-S中的点的路径为特殊路径,并用数组dist[]记录当前每个顶点所对应的最短特殊路径
长度。
Dijkstra算法采用的贪心策略是选择特殊路径长度最短 的路径,将其连接的 V-S 中的顶点加入到集合S中,同时更新数组dist[] —旦S包含了所有顶点,dist[] 就是从源到所有其他顶点之间的最短路径长度 。
算法步骤
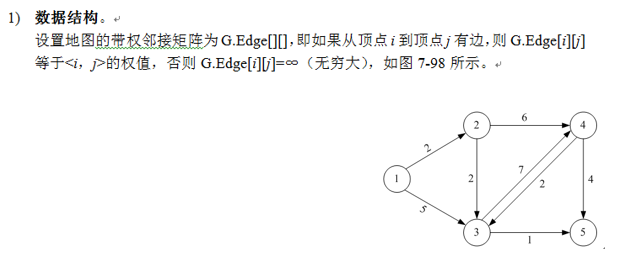
1)数据结构。设置地图的带权邻接矩阵为G.Edge [][], 即如果从源点u到顶点i有边,就令 G.Edge[u][i]等于\
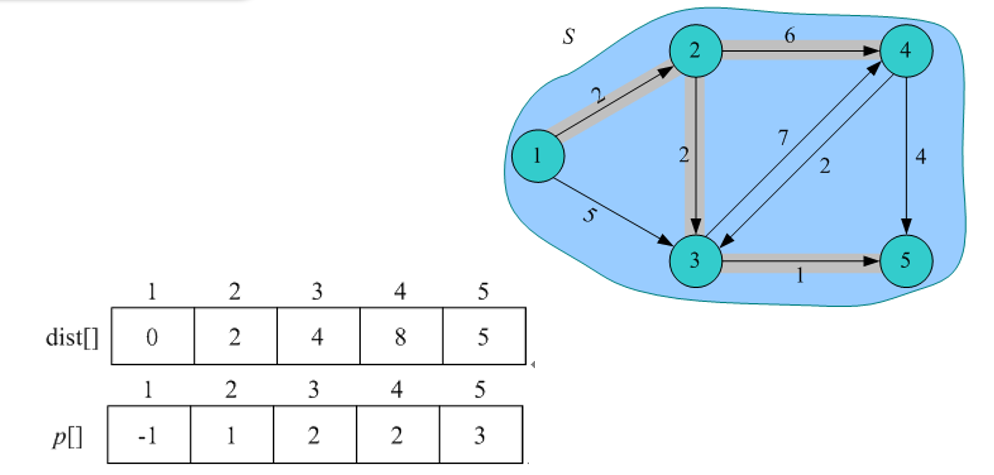
2) 初始化。令集合S={u}, 对千集合 V-S 中的所有顶点X, 初始化dist[i]=G.Edge[u][i],如果源点u到i有边相连,初始化p[i] = u,否则p[i] = -1;
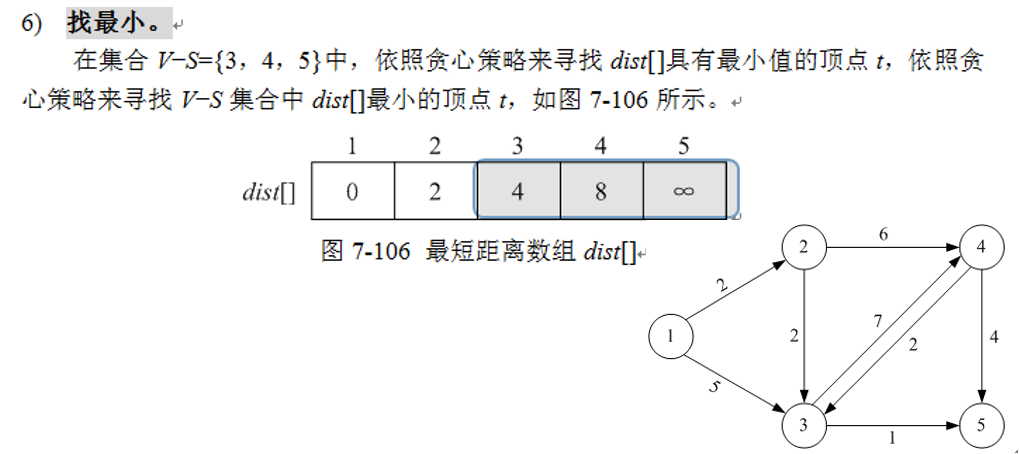
3)找最小。在集合V-S中依照贪心策略来寻找使得dist[j]具有最小值的顶点t,即dist[t] = min(dist[j]|j属于V-S集合) ,则顶点t就是集合V-S中距离源点u最近的顶点
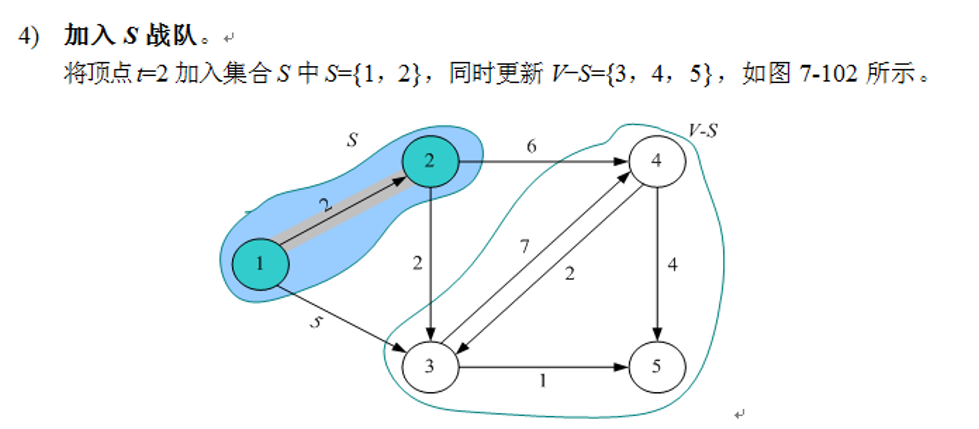
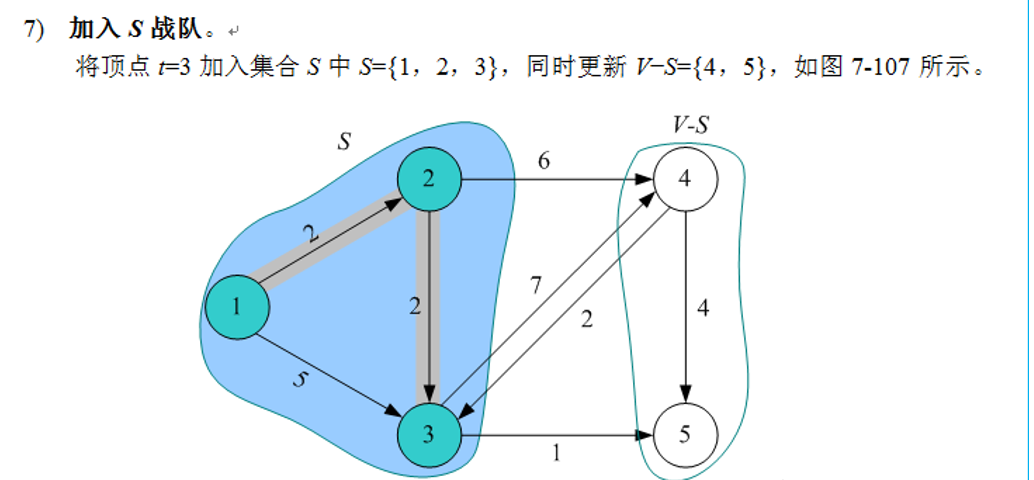
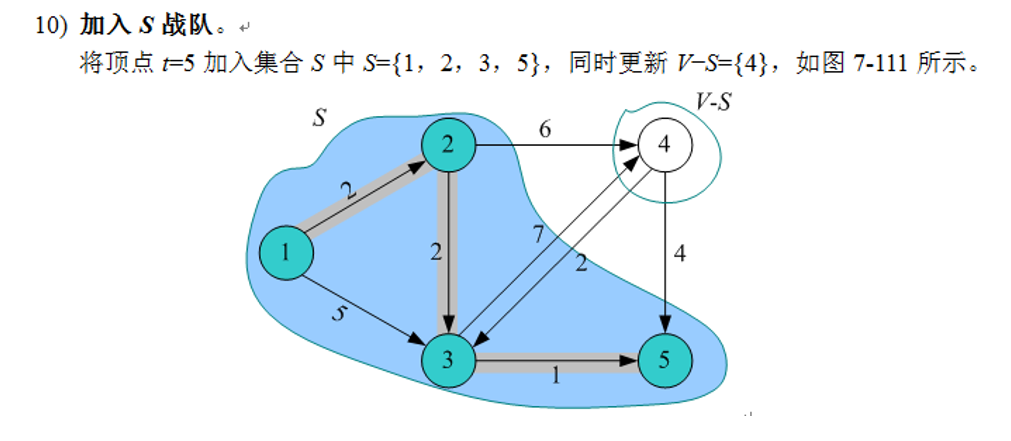
4)加入s战队。把顶点t加入集合s中。同时更新V-S
5)判结束。如果集合V-S为空。算法结束,否则进行6
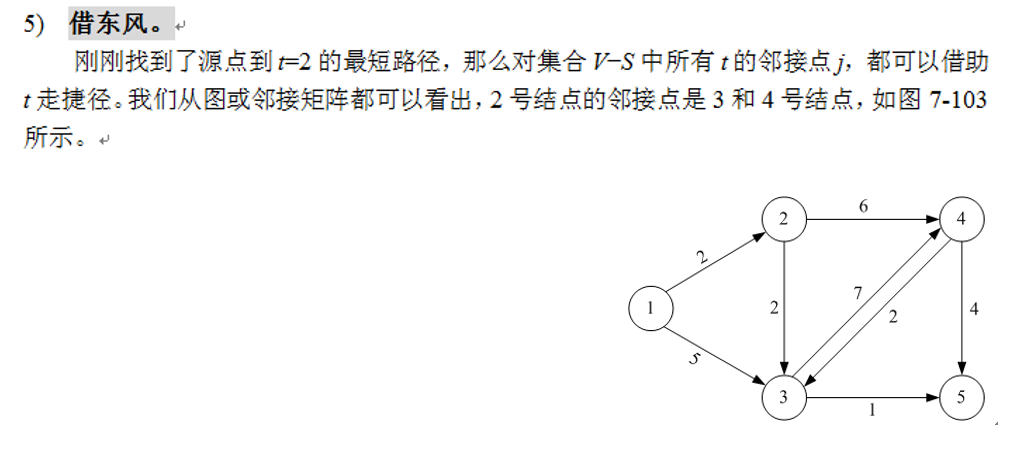
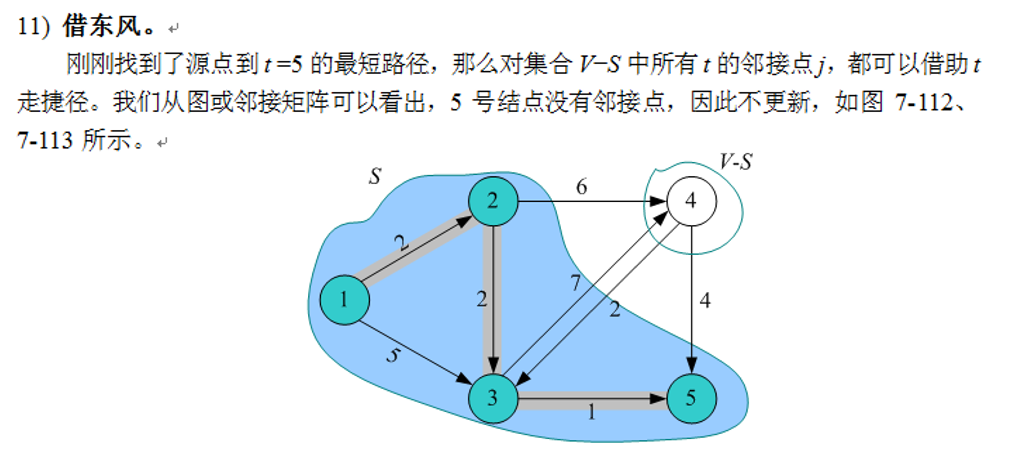
6)借东风。在3)中已经找到了源点到t的最短路径,那么对集合V-S 中所有与顶点t相邻的顶点j,都可以借助t走捷径。如果dis[j]>dist[t]+G.E[i][j] .则dist[j] = dist[t]+G.E[t][j] ,记录顶点j的前驱为t,有p[j] = t 转3)
数据结构
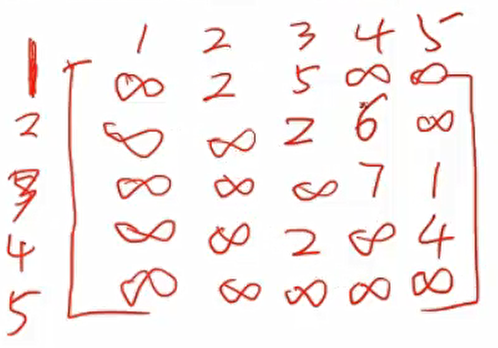





算法分析
1)时间复杂度:在Dijkstra 算法描述中,一共有4个for语句,第1个for语句的执行次数为n,第2个for语句里面嵌套了两个for语句3、4,它们的执行次数均为n,对算法的运行事件贡献最大,当外层循环标号为1时,3、4语句在内层循环的控制下均质性n次,外层循环2从1~n 。因此,该语句的执行次数为$n\times n=n^2$ 算法的时间复杂度为$O(|V|^2)$
2) 空间复杂度,由以上算法可以得出,实现该算法需要的辅助空间包含数组flag、变量i,j,t 和temp所分配的空间,因此,空间复杂度为O(n).
算法优化

代码一览
1 |
|
最短路径:Floyd算法
此算法由Robert W. Floyd(罗伯特·弗洛伊德)于1962年发表在“Communications of the ACM”上。同年Stephen Warshall(史蒂芬·沃舍尔)也独立发表了这个算法。Robert W.Floyd这个牛人是朵奇葩,他原本在芝加哥大学读的文学,但是因为当时美国经济不太景气,找工作比较困难,无奈之下到西屋电气公司当了一名计算机操作员,在IBM650机房值夜班,并由此开始了他的计算机生涯。此外他还和J.W.J. Williams(威廉姆斯)于1964年共同发明了著名的堆排序算法HEAPSORT。堆排序算法我们将在后面学习。Robert W.Floyd在1978年获得了图灵奖。
Dijkstra 算法是求源点到其它各个顶点的最短路径,如果求解任意两个顶点的最短路径, 则需要以每个顶点为源点, 重复调用 n 次 Dijkstra 算法。 完全没必要这么麻烦, 下面介绍的Floyd 算法可以求解任意两个顶点的最短路径今 Floyd 算法又称为插点法, 其算法核心是在顶点i到顶点j之间, 插入顶点k, 看是否能够缩短i和j之间距离(松弛操作)
算法步骤
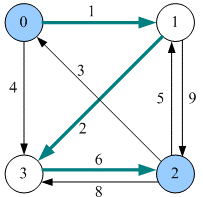
1) 数据结构。 设置地图的节权邻接矩阵为G.Edge[][], 即如果从顶点i到顶点j 有边,就让G.Edge[i][j]=<i, j>的权值,否则G.Edge[i][j] = $\infty$ (无穷大);采用两个辅助数组:最短距离数组dist[i][j], 记录从 i到 j顶点的最短路径长度,前驱数组 $p[i][j]$ 记录从洼肋顶点的最短路径上i顶点的前驱
2) 初始化。初始化dist[i][j]=G.Edge[i][j],如果顶点i到顶点j有边相连,初始化$p[i][j]=i$,否则 $p[i][j]=-1$
3) 插点。其是就是在i,j之间插入顶点k, 者是否能够缩短i和j之间距离(松弛操作)。 如果dist[i][j]>dist[i][k]+dist[k][j], 则dist[i][j]=dist[i][k]+dist[k][j], 记录顶点J的前驱 为:p[i][j]=p[k][j]

1) 数据结构
设置地图地带权邻接矩阵为 $G.E[][]$ 即如果从顶点i到顶点j有边,就让 $G.Edge[][] =
2) 初始化
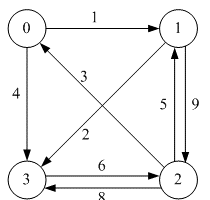
初始化的最短距离数组 $dist[i][j]=G.Edge[i][j]$ 如果 顶点i到顶点j有边相连。初始化前驱数组$p[i][j] = i$ 否则 $p[i][j] = -1$ 初始化后的 $dist[][] 和p[][]$如图
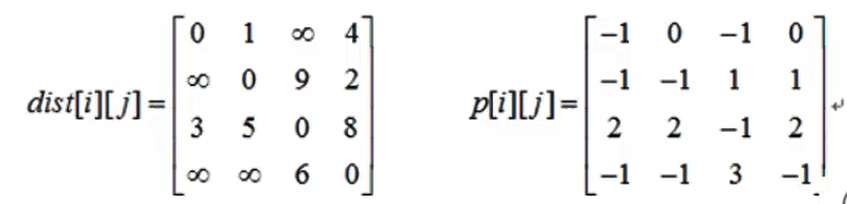
3) 插点
其实就是借点,大家一起借顶点0更新最短距离。如果$dist[i][j]$ >$dist[i][0]+dist[0][j]$ ,则 $dist[i][j] = dist[i][0]+dist[0][j]$
谁可以借顶点0?
看顶点0 的入边,2—0 ,也就是说2 可以借助0点,更新2到其他顶点的最短距离。(程序中未判断谁可以借0点,穷举所有顶点是否可以借0点)
$dist[2][1]:dist[2][1] = 5>dist[2][0]+dist[0][1]= 4$ 则更新 $dist[2][1] = 4,p[2][1] = 0$
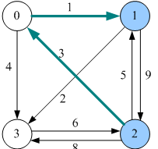

4)插点
大家一起借顶点1更新最短距离,谁可以借顶点1呢?
看顶点1 的入边,顶点0,2都可以借助1点,更新其到其他顶点的最短距离
更新的时候是根据现有的dist值来的,不是原始的两条边!
$dist[0][2]:dist[0][2]=\infty>dist[0][1]+dist[1][2]= 10$则更新$dist[0][2]=10,p[0][2]=1$
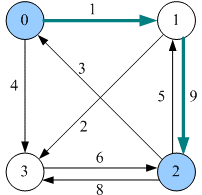
同样的,$dist[0][3] : dist[0][3] = 4 > dist[0][1]+dist[1][3] = 3$ 所以更新
$dist[2][3] = 7 > dist[2][1]+[1][3] = 6$ ,所以更新

5)插点(k=2)
谁可以借顶点2更新最短距离呢?
dist[1][0] = inf > dist[1][2]+dist[2][0]=12所以更新dist[3][0] = inf > dist[3][2]+dist[2][0]= 9所以更新dist[3][1] = inf > dist[3][2]+dist[2][1](经过0点,是复杂路径)=10所以更新,注意这里的p[i][j]要改成p[2][1]
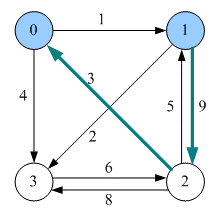

6)插点(k=3)
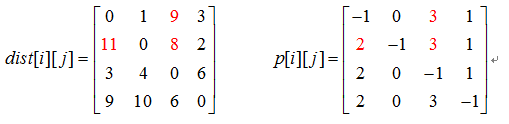
算法分析
1)时间复杂度 三层for语句循环,时间复杂度为$O(n^3)$
2) 空间复杂度:采用两个辅助数组,最短距离数组和前驱数组,因此空间复杂度为$O(n^2)$
尽管Floyd算法的时间复杂度为$O(n^3)$ 但其代码简单,对中等输入规模来说,仍然相当有效。如果用Dijkstra算法求解各个顶点之间的最短路径,则需要以每个顶点为源点调用一次,一共调用n次,齐总时间复杂度也为$O(n^3) $。特别注意的是,Dijkstra算法无法处理带负权值边的图,Floyd算法可以处理带负权值边的图,但不允许图中包含带负权值边组成的回路。可以学习另一个解决负权值边的最短路径算法 Bellman-Ford 算法
1 |
|
最小生成树:Prim算法
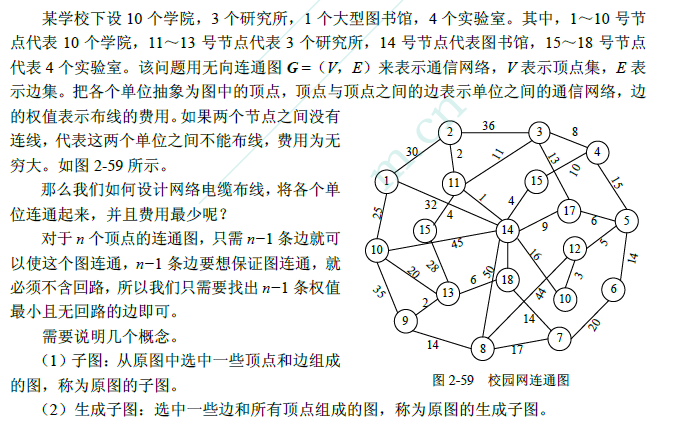

注意,n-1条边,保证没有回路! 所以要一边找,一边避免回路
算法设计
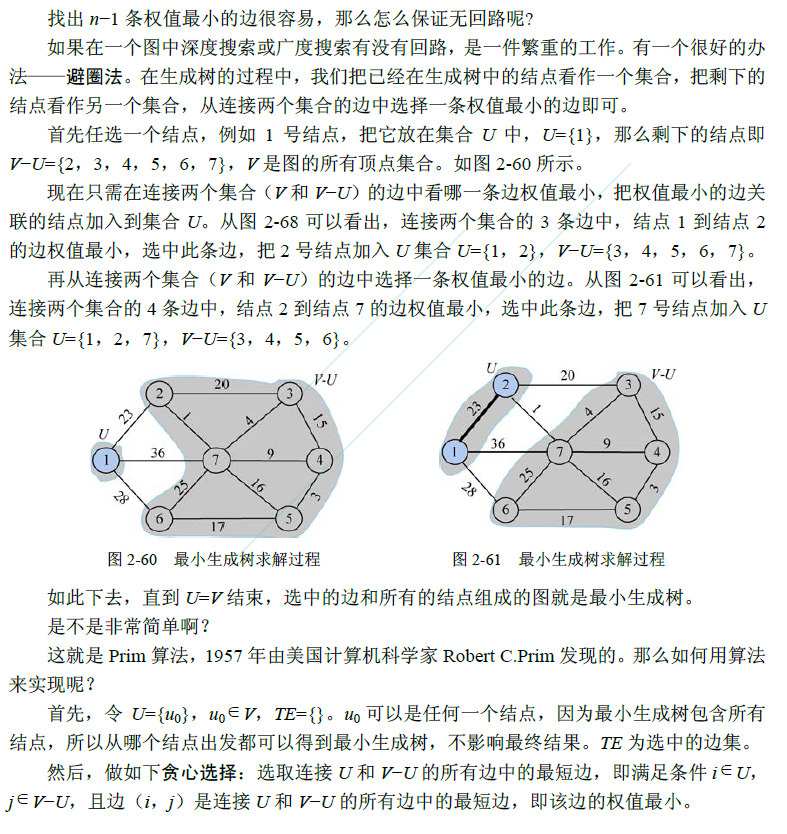

步骤
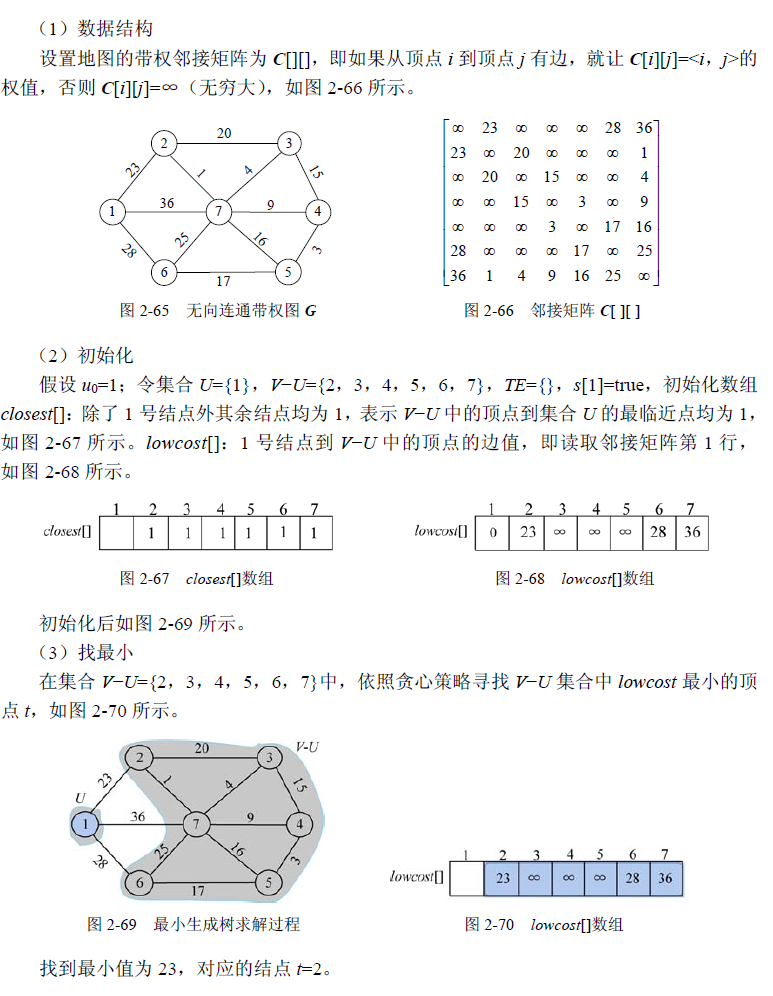
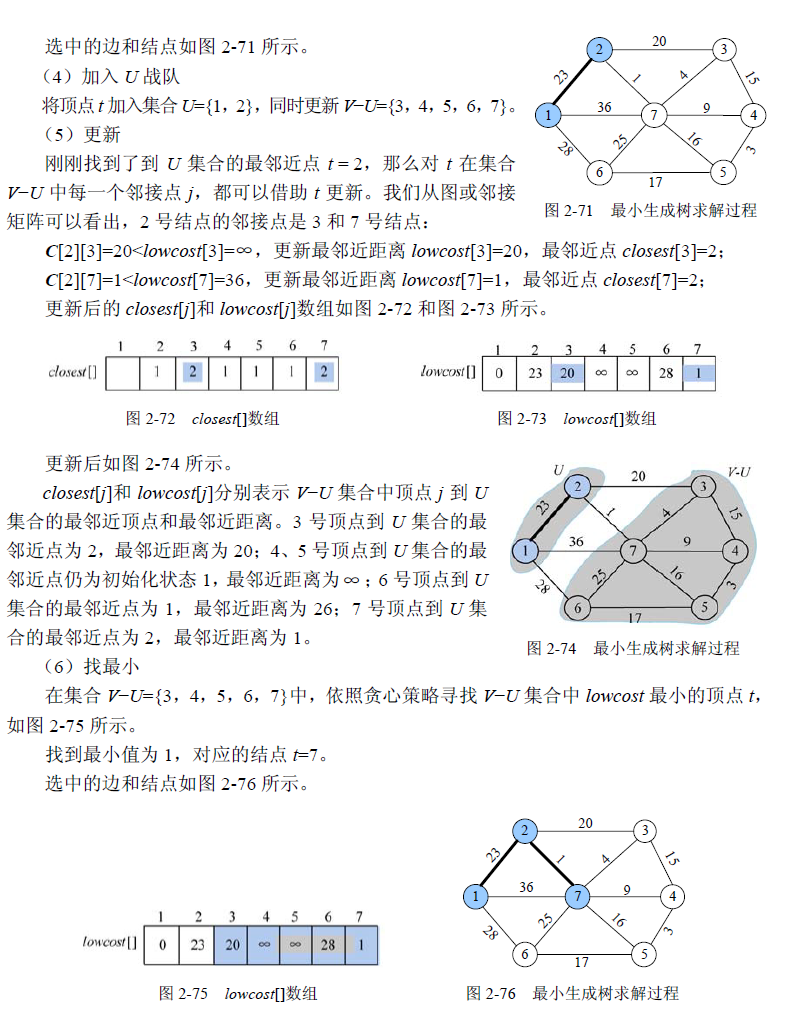
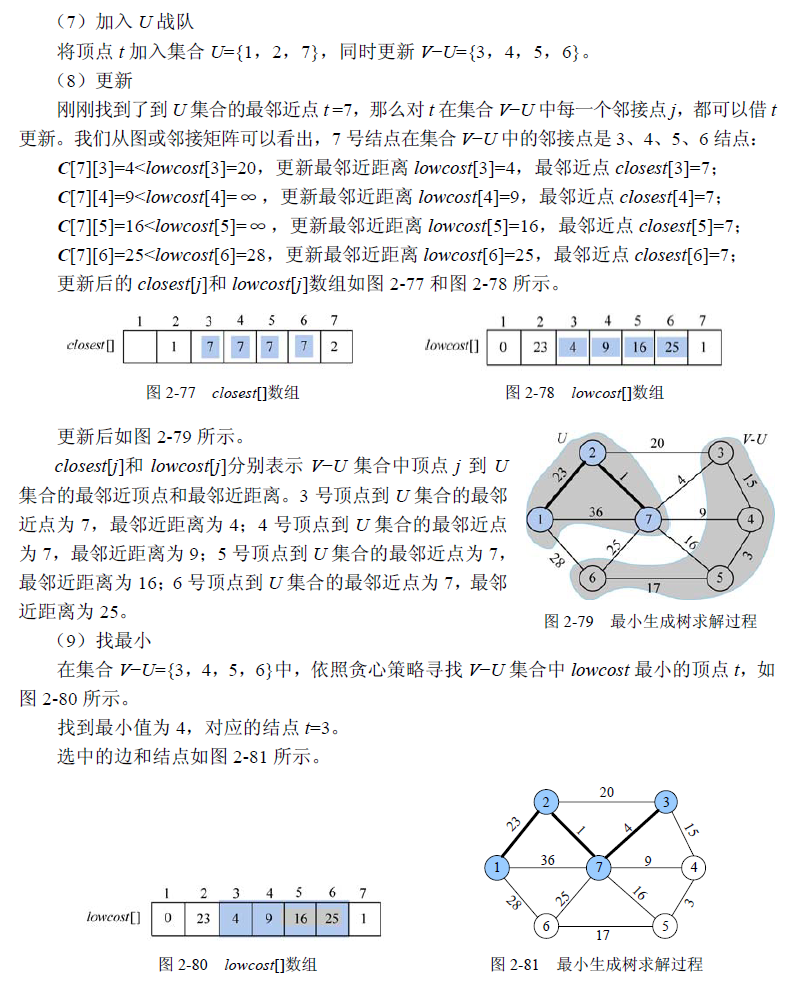
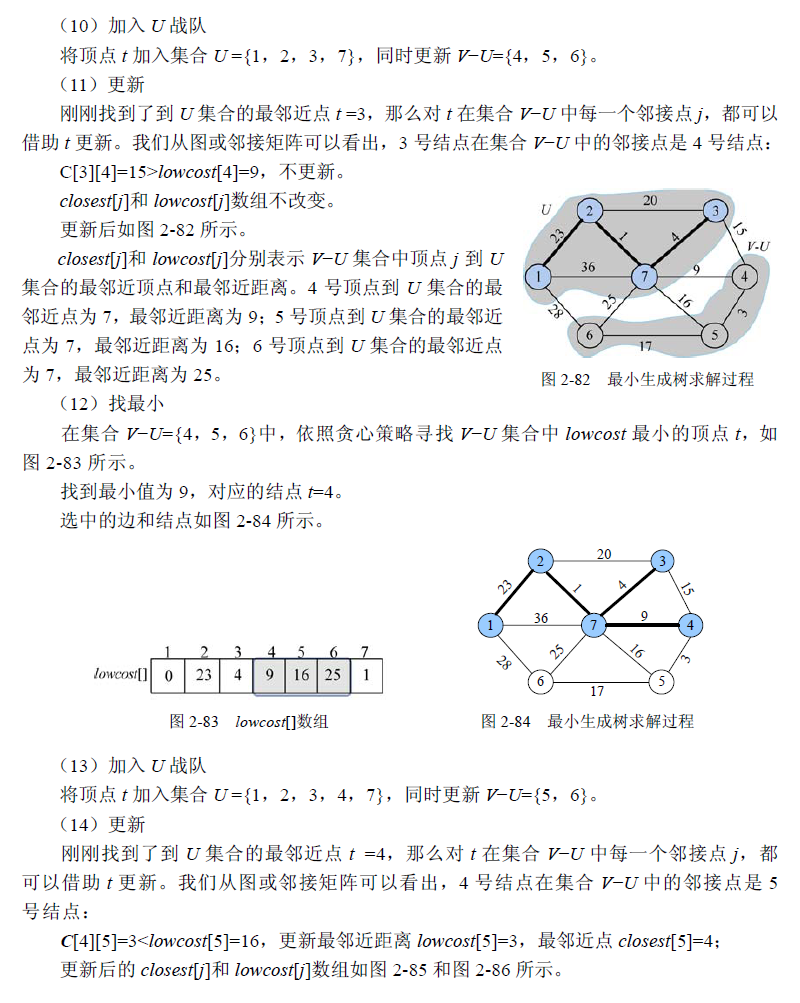
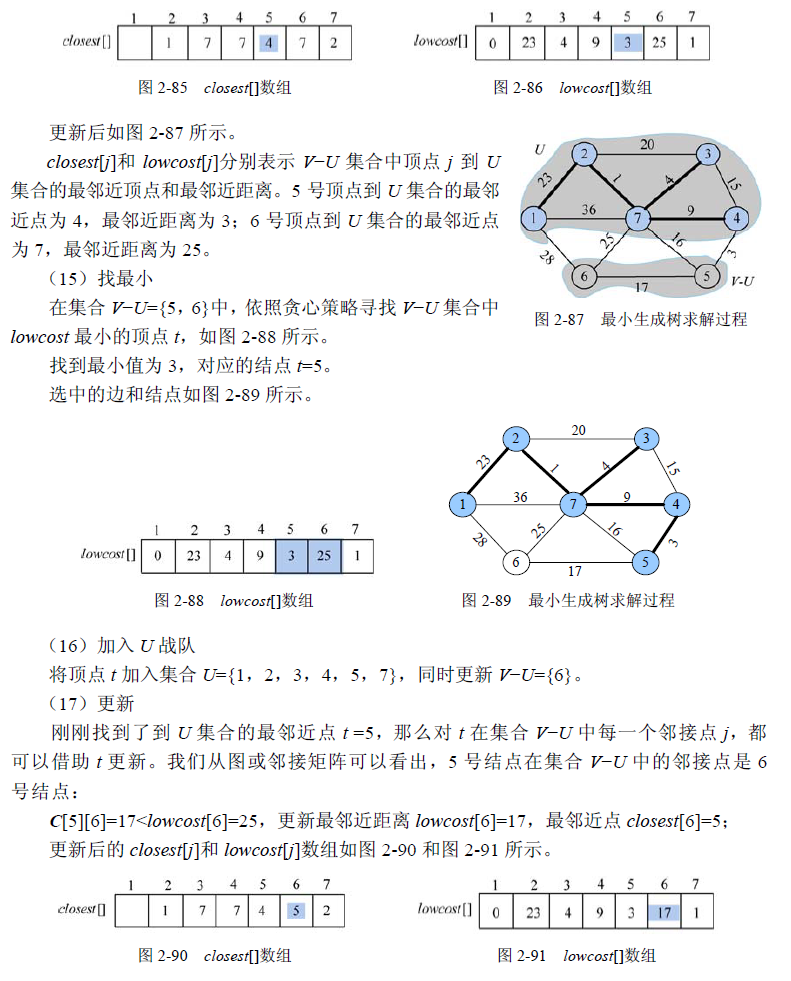
设 G =(V,E)是无向连通带权图,如图2-65 所示。
1 | //program 2-6 |
算法分析
(1)时间复杂度:在Prim(int n,int u0,int c[N][N])算法中,一共有4 个for 语句,第①个for 语句的执行次数为n,第②个for 语句里面嵌套了两个for 语句③、④,它们的执行次数均为n,对算法的运行时间贡献最大。当外层循环标号为1 时,③、④语句在内层循环的控制下均执行n 次,外层循环②从1~n。因此,该语句的执行次数为n*n=n²,算法的时间复杂度为$O(n^2 )$。这里的n指的是边的数量,即 $O(|V|^2)$ , 时间复杂度不依赖 $|E|$
(2)空间复杂度:算法所需要的辅助空间包含i、j、lowcost 和closest,则算法的空间复杂度是$O(n)$
算法可视化在这里
https://www.cs.usfca.edu/~galles/visualization/Prim.html
算法优化
Prim算法可以从两个方面优化:
(1)for 语句③找lowcost 最小值时使用优先队列,每次出队一个最小值,时间复杂度为logn,执行n 次,总时间复杂度为O( nlogn)。
(2)for 语句④更新lowcost 和closest 数据时,如果图采用邻接表存储,每次只检查t的邻接边,不用从1~n 检查,检查更新的次数为E(边数),每次更新数据入队,入队的时间复杂度为logn,这样更新的时间复杂度为O( Elogn)。
最小生成树:Kruskal算法
算法设计


图解
每次选最短边,不要有回路
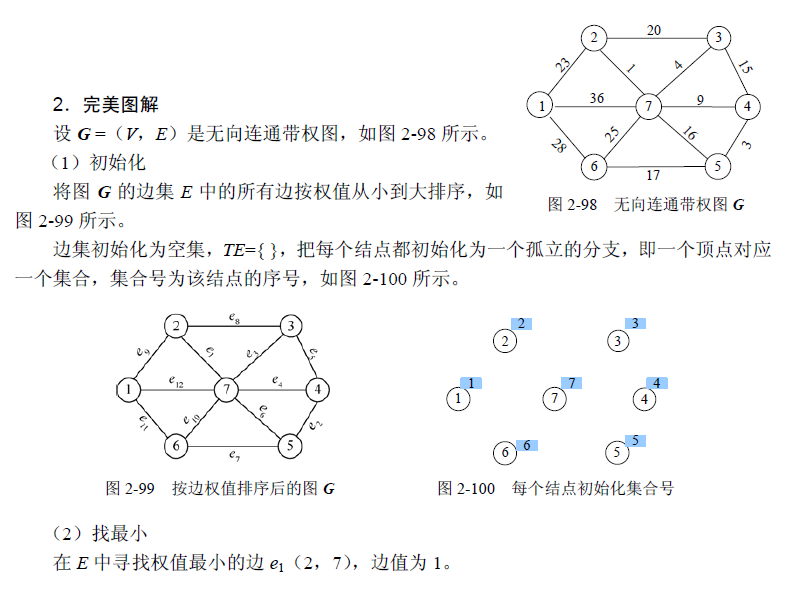
我们使用边集数组存储这张图,便于排序


代码一览
1 |
|
算法分析
(1)时间复杂度:算法中,需要对边进行排序,若使用快速排序,执行次数为$e\log e$,算法的时间复杂度为 $O(e\log e)$ ,如果使用对来存放边的集合,那么每次选择权值最小的边只需要$O(\log|E|)$ 的实践,而合并集合需要n−1 次合并,每次为$O(n)$,合并集合的时间复杂度为$O(n^2)$。
(2)空间复杂度:算法所需要的辅助空间包含集合号数组 nodeset[n],则算法的空间复杂度是 $O(n)$ 。
算法优化
该算法合并集合的时间复杂度为 O(n^2),我们可以用并查集的思想优化,使合并集合的时间复杂度降为$O(e\log e)$,优化后的程序如下。
1 | //program 2-7-1 |
两种算法的比较
(1)从算法的思想可以看出,如果图G 中的边数较小时,可以采用Kruskal 算法,因为Kruskal 算法每次查找最短的边;边数较多可以用Prim 算法,因为它是每次加一个结点。可见,Kruskal 算法适用于稀疏图($e\log(e)$如果e及其大,会比 $n^2 $ 还大),而Prim 算法适用于稠密图。
(2)从时间上讲,Prim 算法的时间复杂度为 $O(V^2)$,Kruskal 算法的时间复杂度为$O(e\log e)$ 。
(3)从空间上讲,显然在Prim 算法中,只需要很小的空间就可以完成算法,因为每一次都是从V−U 集合出发进行扫描的,只扫描与当前结点集到U 集合的最小边。但在Kruskal算法中,需要对所有的边进行排序,对于大型图而言,Kruskal 算法需要占用比Prim 算法大得多的空间。