高阶微分方程

可降阶的微分方程

二阶以及二阶以上的微分方程称之为高阶微分方程

一般来说，微分方程的阶数越高，求解的难度也就越大。求高阶方程的一个常用方法就是降低阶数

对二阶方程 $y’’ = f(x,y,y’)$

如果能用变量代换把它化成一阶方程，那么就可以用一阶微分方程的求解方法来解决了。

下面对二阶方程中的三种容易降阶的情形进行讨论。

$y^{‘’} = f(x) $型微分方程

这类方程的特点就是左边为未知函数的二阶导数，右边只是自变量x的函数，只要对方程接连积分两次，就能得到原方程的含有两个任意常数的通解。

$y^{‘’} =f(x,y’)$ 型微分方程

特点是不含未知函数，因此设 $y’ = z(x)$ 则 $y’’ = \frac{dz}{dx}=z’$ 原方程化为一阶方程(可分离变量/齐次/一阶线性齐次/一阶线性非齐次/伯努利方程/全微分方程) ： $z’ = f(x,z)$

设其通解为 $z = \phi(x,C_1)$ 则得到一阶方程 $y’ = \phi(x,C_1)$ 再一次积分，得到原方程的通解。

$y=\int\phi(x,C_1)dx+C_2$

例题： $xy’’ = y’-xy’^2$ 这是比较复杂的一道微分方程

1.首先我们令 $z=y’$, 那么 $z’ = y’’$ 于是 $xz’ = z-xz^2$ 变型得到 $\frac{dz}{dx} -\frac{z}{x}= -z^2 $ (伯努利方程)

2.$P_1(x) = -\frac{1}{x},Q_1(x) = -1$

3.然后用解伯努利的方程的方法。令 $w = z^{1-2} = z^{-1}$ 则 $\frac{dw}{dx} =-1\cdot z^{-2}\frac{dz}{dx}$ ,带入伯努利方程得到 $\frac{dw}{dx} + (1-n)P(x)w=(1-n)Q(x)$ 也就是 $\frac{dw}{dx}+(-1)(-\frac{1}{x})w = (1-2)\cdot -1$ 化简得到 $\frac{dw}{dx} +\frac{w}{x} = 1$ （一阶线性非齐次方程),$P_2(x) = \frac{1}{x},Q_2(x)= 1$

4.然后利用解一阶线性非齐次方程的方法。其对应的一阶线性齐次方程为 $\frac{dw}{dx} + \frac{w}{x} = 0$ ,解得 $w=\frac{C}{x}$ .令一阶线性非齐次方程的通解为$w=\frac{u(x)}{x}$, $\frac{du}{dx} = w+x\frac{dw}{x}$ . 代入非齐次方程式得到$\frac{du}{dx}\cdot\frac{1}{x} = Q(x) , \frac{du}{dx} = x, u = \frac{1}{2}x^2+C$ . 于是通解 $w = \frac{u(x)}{x} = \frac{1}{2}x+\frac{C}{x}$

5.因此 $z=w^{-1}=\frac{2x}{x^2+2C}=y’, y=\int\frac{2x}{x^2+2C} dx = ln|x^2+C_1|+C_2$

$y^{‘’} =f(y,y’)$ 型微分方程

这类方程的特点就是不含有自变量

令 $y’ = z(y)$, 则 $y’’ = \frac{dz}{dx}=\frac{dz}{dy}\cdot\frac{dy}{dx} = z\frac{dz}{dy}$

故方程化为 $z\frac{dz}{dy} = f(y,z)$

设其通解为 $z=\phi(y,C_1)$，即得 $y’ = \frac{dx}{dy}=\phi(y,C_1)$ 分离变量后积分，得到原方程的通解.

线性微分方程的性质

定理1

设 $y_1(x),y_2(x)$ 是二阶线性齐次方程 $y’’+p_1(x)y’ +p_2(x)y=0$ 的两个特解，则 $y = C_1y_1(x)+C_2y_2(x) $也应该是方程的解，其中$C_1,C_2$ 是任意常数。

注意：$y=C_1y_1(x)+C_2y_2(x)$ 虽有两个任意常数，他们可能不是独立的，所以不一定是所给二阶方程的通解。

例如，$y_1(x)$ 是某二阶齐次方程的解，则 $y_2(x)=2y_1(x)$ 也是齐次方程的解。

但是 $C_1y_1(x)+C_2y_2(x) = (C_1+2C_2)y_1(x)$并不是通解

函数线性相关和线性无关

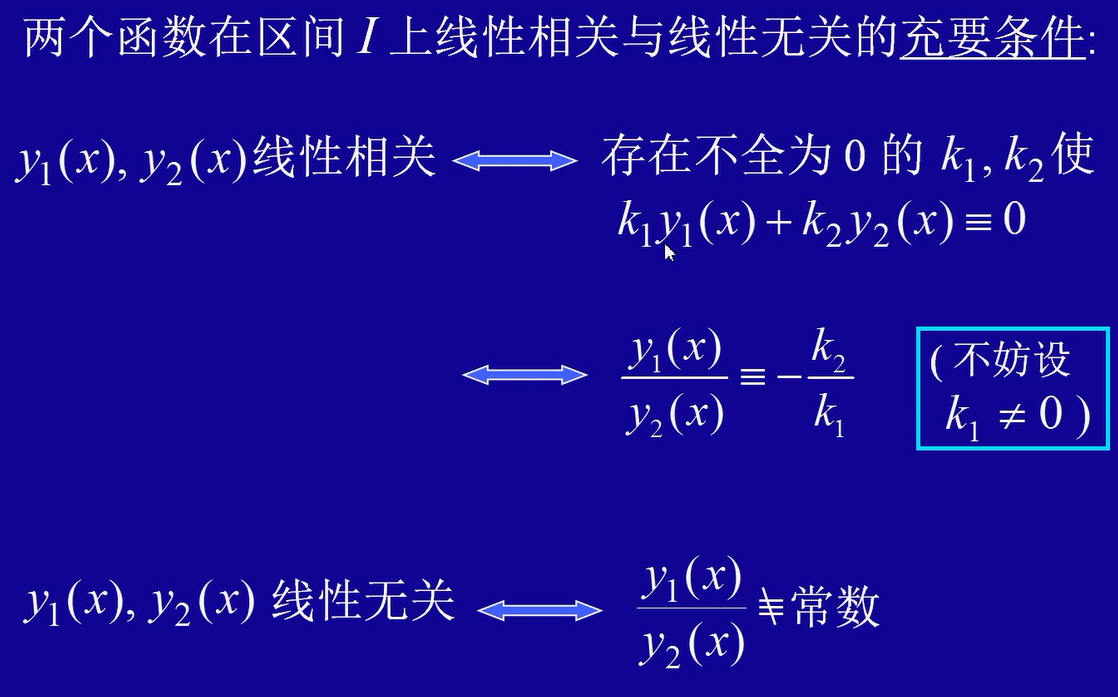
定理2

设$y_1(x),y_2(x)$ 是二阶线性齐次方程的两个线性无关的特解，则 $y=C_1y_1(x)+C_2y_2(x)$ 是方程的通解，其中$C_1,C_2$ 是任意常数

定理3

设 $y^{\%}(x)$ 是二阶非齐次方程 $y’’+p_1(x)y’+p_2(x)y =q(x)$ 的一个特解，$Y(x)$ 是相应的齐次方程的通解，则 $y = Y(x)+y^{\%}(x)$ 是非齐次方程(1) 的通解。

定理4

设 $y_1(x),y_2(x)$ 分别是二阶线性非齐次方程 $y’’+p_1(x)y’+p_2(x) = q_1(x)$ 和 $y’’+p_1(x)y’+p_2(x) = q_2(x)$ 的解，则 $y(x) = ay_1(x) +by_2(x)$ 的解，则 $y(x)= ay_1(x)+by_2(x)$ 是非齐次方程 $y’’+p_1(x)y’+p_2(x)y = aq_1(x)+bq_2(x)$ 的解。(非齐次方程解的叠加原理)

以上结论可以推广到n阶线性微分方程当中去

二阶常系数线性齐次方程的解

二阶常系数齐次线性微分方程 $y’’ +py’+qy=0$ (p,q为常数) (1)

因为r为常数时，函数 $e^{rx}$ 和它的导数只差一个常数因子，所以令 (1) 的解为 $y=e^{rx}$ (r为待定常数)，带入(1) 得 $(r^2+pr+q)e^{rx}=0\Rightarrow r^2+pr+q=0$ （2）。我们称(2) 为微分方程 (1) 的特征方程，其根称为特征根

1 当 $p^2-4q>0$ 时，（2）有两个相异实根 $r_1,r_2$ ，则微分方程有两个线性无关的特解： $y_1=e^{r_1x},y_2=e^{r_2x}$ 因此方程的通解为 $y=C_1e^{r_1x}+C_2e^{r_2x}$

2 当 $p^2-4q=0$ 时，特征方程有两个相等实根 $r_1=r_2=\frac{-p}{2}$ 则微分方程有一个特解 $y_1=e^{r_1x}$ ，原方程的通解为 $y=(C_1+C_2x)e^{r_1x}$

3 当 $p^2-4q<0$ 时，特征方程有一对共轭复根 $r_1=\alpha+i\beta,r_2=\alpha-i\beta$ 这时原方程有两个复数解：
$y_1=e^{(\alpha+i\beta)x}=e^{\alpha x}(cos\beta x+isin\beta x)$

$y_2=e^{(\alpha-i\beta)x}=e^{\alpha x}(cos\beta x-isin\beta x)$

原方程的通解为 $y=e^{\alpha x}(C_1cos\beta x+C_2sin\beta x)$